Ученик
(110),
закрыт
12 лет назад
Татьяна
Мыслитель
(9993)
12 лет назад
Точка N – середина отрез
Найдём координаты вектора ВС:
ВС=ВА+АС=АС-АВ=(9-(-3); 6-0; -2-2)=(12;6;-4).
Выразим вектор AN и найдём его координаты:
AN=AB+BN=AB+1/2BC=(-3;0;2)+1/2(12;6;-4)=
=(-3;0;2)+(6;3;-2)=(3;3;0)
Находим длину медианы AN – вектора AN:
AN=кв. корень (3^2+3^2+0^2)=кв. корень (18)=3*кв. корень (2).
diamond –
Гуру
(4795)
12 лет назад
Находиш точку N по принципу среднее арифметическое координат точек В и С. Затем длинна = корень квадратный из суммы квадратов координат (x^2+y^2+z^2). Чуть не забыл – точка А – ето начало координат (0;0;0)
Matricfria
Мыслитель
(5124)
12 лет назад
N – середина стороны ВС. Тогда вектор АN = 1/2(АВ + АС) = 1/2(-3+9; 0+6; 2+(-2)) =
=1/2(6;6; 0) = (3; 3; 0)
Теперь нахом длину медианы AN. Она рaвна длине вектора AN.
AN = корень квадратный (3^2+3^2+0^2)= корень квадратный из 18 =
=3корень квадратный из 2
Найти медиану треугольника по координатам вершин
Как найти медиану если даны координаты вершин треугольника?
Чтобы найти медиану треугольника по координатам его вершин, применим формулы координат середины отрезка и формулу расстояния между точками.
Рассмотрим нахождение медианы на конкретном примере.
 Дано: ΔABC,
Дано: ΔABC,
A(-11;12), B(3;8), C(-1;6),
AF — медиана.
Найти: AF
Решение:
1) Так как AF — медиана треугольника ABC, то F — середина BC.
По формулам координат середины отрезка:
![]()
![]()
Итак, F(1;7).
2) По формуле расстояния между точками
![]()
![]()
![]()
Ответ: 13.
Ответ на первый ответ постой:
Скалярное произведение есть скаляр, равный произведению модулей на косинус угла между ними:
А=|p|*|q|*cos(p, q) = 3 *1* cos (pi/3) = 3*0,5=1,5..
Со вторыми заданиями немного сложнее:
Сначала установим условно вектор q на оси х, тогда получим, что оба вектора начинаются в 0 и имеют между собой заданный угол..
Разложим оба вектора p и q на взаимно ортогональные составляющие:
px=|p|cos (п/3)=3*0,5=1,5
py=|p|sin (п/3)=3*0,86=2,6
qx=|q|=1
qy=0
Далее согласно заданным выражениям AB = 2p – q; AC = 3p + 2q произведём вычисления для каждой спроецированной компоненты..
AB = 2p – q; AC = 3p + 2q
АВх=2*1,5-1=2
АВу=2*2,6=5,2
АСх=3*1,5+2=6,5
АСу=3*1,5=4,5
Итак, мы задали точку А(0;0), получили точки В(2;5,2) С(6,5;4,5)..
Вектор ВС задаётся точкой А и В..
Теперь всё просто: находим длину отрезка ВС по известным координатам:
|BC|=sqrt((6,5-2)^2+(5,2-4,5)^2)= 4,5..
отношение cos a=(5,2-4,5)/4,5 есть угол относительно оси абсцисс, относительно которой мы и отсчитываем угол а=81 град=1,41 рад..
Модуль и угол задают вектор ВС..
Чтобы найти длину медианы нужно найти точку М, которая делит ВС напополам 4,5/2 = 2,25..
Из подобия прямоугольного треугольника, построенного на точек М стороны
(6,5-2)/2+2 = 4,25..
(5,2-4,5)/2+4,5= 4,85..
Это координаты точки М (4,25;4,85)..
Теперь находим АМ=sqrt((4,25)^2+(4,85)^2)=6,45..
Это и есть искомая длина медианы..
Найти медиану треугольника по координатам вершин
Как найти медиану если даны координаты вершин треугольника?
Чтобы найти медиану треугольника по координатам его вершин, применим формулы координат середины отрезка и формулу расстояния между точками.
Рассмотрим нахождение медианы на конкретном примере.
Дано: ΔABC,
1) Так как AF — медиана треугольника ABC, то F — середина BC.
Медиана треугольника
Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.
На рисунке 1 медианой является отрезок BD .
Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).
Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)


Поскольку отрезок BD является медианой, то

что и требовалось доказать.
Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.
Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,


Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.
Следствие . Все три медианы треугольника пересекаются в одной точке.
Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).

Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.
Определение . Точку пересечения медиан треугольника называют центроидом треугольника.
Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна  площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).
площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).
Длина медианы треугольника
Медиана треугольника (лат. mediāna — средняя) ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны, а также прямая, содержащая этот отрезок.
Каждый треугольник имеет ровно три медианы, по одной из каждой вершины, и все они пересекаются друг с другом в центре треугольника. В случае равнобедренного и равностороннего треугольников, медиана делит пополам любой угол в вершине у которого две смежные стороны равны.
Калькулятор длины медианы треугольника
Онлайн калькулятор расчета длины медианы треугольника при условии, что известны координаты его вершин. Нахождение длины трех медиан треугольника
Формула расчета длины медианы
- a,b,c — Длина сторон треугольника.
Пример расчета медиан:
Даны точки A( 1 , 5 ), B( 8 , 9 ) и C( 5 , 6 ). Найдите медианы треугольника.
Получаем:
A( 1 , 5 ) B( 8 , 9 ) C( 5 , 6 )
Решение:
Шаг 1:
Найдем длину сторон a,b,c используя формулу
Найдем длину стороны A между точками B( 8 , 9 ) and C( 5 , 6 )
a = √((5 — 8) 2 + (6 — 9) 2 )= 4.242
Найдем длину стороны B между точками C( 5 , 6 ) и A( 1 , 5 )
b = √((1 — 5) 2 + (5 — 6) 2) = 4.123
Найдем длину стороны C между точками A( 1 , 5 ) и B( 8 , 9 )
c = √((8 — 1) 2 + (9 — 5) 2) = 8.062
Шаг 2:
Полученные значения a,b,c применяем в формулы
ma = (1/2) √2c 2 + 2b 2 — a 2
mb = (1/2) √(2c 2 + 2a 2 — b 2 )
mc = (1/2) √(2a 2 + 2b 2 — c 2 )
- ma = (1/2)√(2(8.062) 2 + 2(4.123) 2 — 4.242 2 )= 6.042
- mb = (1/2)√(2(8.062) 2 + 2(4.242) 2 — 4.123 2 )= 6.103
- mc = (1/2)√2(4.242) 2 + 2(4.123) 2 — 8.062 2 = 1.118
[spoiler title=”источники:”]
http://www.resolventa.ru/spr/planimetry/mediana.htm
http://wpcalc.com/median-triangle/
[/spoiler]

информация о
следующих вебинарах и чатах на сайте ИДО

2. Даны вершины треугольника
Составить:
а) уравнение стороны АВ и найти ее длину,
b) уравнение медианы BM и найти ее длину,
с) уравнение высоты СН и найти ее длину,
d) косинус угла между медианой ВМ и высотой СН.
78
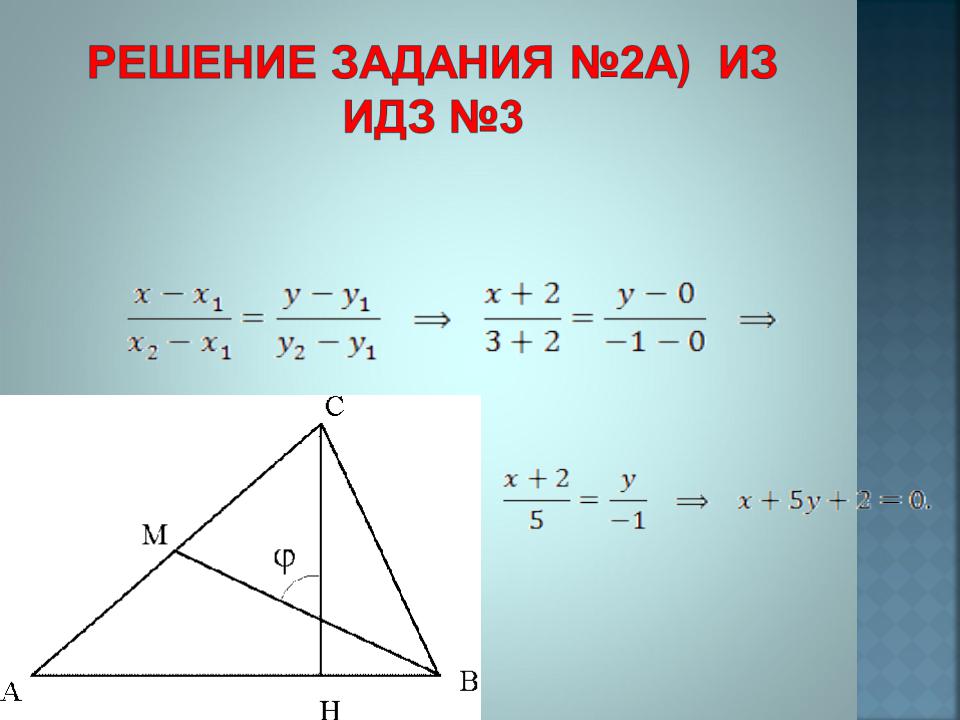
а) Для составления уравнения стороны АВ воспользуемся уравнением прямой, проходящей через две точки:
79
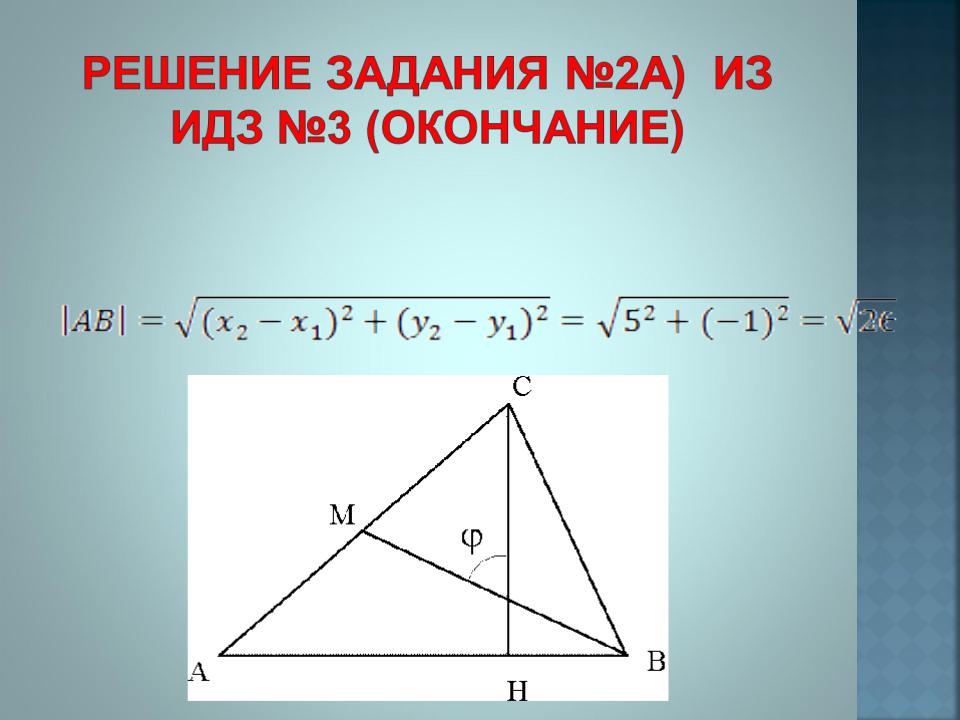
Длину стороны АВ найдем как расстояние между двумя точками
80

b) Вектор медианы треугольника равен полусумме векторов его сторон, т.е.
Длина медианы есть модуль вектора
81
