Все формулы медианы треугольника
Медиана – отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M – медиана, отрезок |AO|
c – сторона на которую ложится медиана
a, b – стороны треугольника
γ – угол CAB
Формула длины медианы через три стороны, (M):
Формула длины медианы через две стороны и угол между ними, (M):
- Подробности
-
Автор: Administrator
-
Опубликовано: 08 октября 2011
-
Обновлено: 13 августа 2021
У этого термина существуют и другие значения, см. Медиана.
Треугольник и его медианы.
Медиа́на треуго́льника (лат. mediāna — средняя) ― отрезок в треугольнике, соединяющий вершину треугольника с серединой стороны, противоположной этой вершине.
Иногда медианой называют также прямую, содержащую этот отрезок, а иногда длину этого отрезка.
Точка пересечения медианы со стороной треугольника называется основанием медианы.
Если 












Связанные определения[править | править код]
Точка пересечения медиан делит каждую медиану на два отрезка.
Отрезок от вершины до точки пересечения называется предмедианой, а отрезок от точки пересечения до противоположной стороны постмедианой[1].
В частности можно сказать, что в любом треугольнике отношение предмедианы к постмедиане равно двум.
Свойства[править | править код]
Основное свойство[править | править код]
Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Свойства медиан равнобедренного треугольника[править | править код]
В равнобедренном треугольнике две медианы, проведенные к равным сторонам треугольника, равны, а третья медиана одновременно является биссектрисой и высотой. Верно и обратное: если в треугольнике две медианы равны, то треугольник — равнобедренный, а третья медиана одновременно является биссектрисой и высотой угла при своей вершине.
У равностороннего треугольника все три медианы равны.
Если медианы равнобедренного треугольника, проведённые к боковым сторонам, пересекаются под прямым углом, то косинусы углов при основании этого треугольника равны 

Свойства оснований медиан[править | править код]
- Теорема Эйлера для окружности девяти точек: основания трёх высот произвольного треугольника, середины трёх его сторон (основания его медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (так называемой окружности девяти точек).
- Отрезок, проведенный через основания двух любых медиан треугольника, является его средней линией. Средняя линия треугольника всегда параллельна той стороне треугольника, с которой она не имеет общих точек.
- Следствие (теорема Фалеса о параллельных отрезках). Средняя линия треугольника равна половине длины той стороны треугольника, которой она параллельна.
- Теркем доказал теорему Теркема[2]. Она утверждает, что если окружность девяти точек пересекает стороны треугольника или их продолжения в 3 парах точек (в 3 основаниях соответственно высот и медиан), являющихся основаниями 3 пар чевиан, то, если 3 чевианы для 3 из этих оснований пересекаются в 1 точке (например 3 медианы пересекаются в 1 точке), то 3 чевианы для 3 других оснований также пересекаются в 1 точке (то есть 3 высоты также обязаны пересечься в 1 точке).
Другие свойства[править | править код]
- Если треугольник разносторонний (неравносторонний), то его биссектриса, проведённая из любой вершины, лежит между медианой и высотой, проведёнными из той же вершины.
- Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
- Медиана делит пополам любой отрезок, параллельный стороне, к которой проведена эта медиана.
- Треугольник делится тремя медианами на шесть равновеликих треугольников. Центры описанных окружностей этих шести треугольников лежат на одной окружности, которая называется окружностью Ламуна.
- Из отрезков, образующих медианы, можно составить треугольник, площадь которого будет равна 3/4 от всего треугольника. Длины медиан удовлетворяют неравенству треугольника.
- В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
- Большей стороне треугольника соответствует меньшая медиана.
- Отрезок прямой, симметричный или изогонально сопряжённый внутренней медиане относительно внутренней биссектрисы, называется симедианой треугольника. Три симедианы проходят через одну точку — точку Лемуана.
- Медиана угла треугольника изотомически сопряжена самой себе.
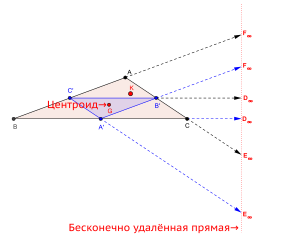
Бесконечно удаленная прямая — трилинейная поляра центроида
- Трилинейная поляра центроида (точки пересечения трех медиан) — бесконечно удаленная прямая (см. рис.).
Основные соотношения[править | править код]
Чтобы вычислить длину медианы, когда известны длины сторон треугольника, применяется теорема Аполлония (выводится через теорему Стюарта или достроением до параллелограмма и использованием равенства в параллелограмме суммы квадратов сторон и суммы квадратов диагоналей):
- где
— медианы к сторонам треугольника
соответственно.
В частности, сумма квадратов медиан произвольного треугольника составляет 3/4 от суммы квадратов его сторон:
.
Обратно, можно выразить длину произвольной стороны треугольника через медианы:
- где
— медианы к соответствующим сторонам треугольника,
— стороны треугольника.
Площадь 
- где
— полусумма длин медиан.
Вариации и обобщение[править | править код]
- Чевиана — отрезок в треугольнике, соединяющий вершину треугольника с точкой на противоположной стороне.
См. также[править | править код]
- Биссектриса
- Высота треугольника
- Инцентр
- Симедиана
- Центроид
- Чевиана
Примечания[править | править код]
- ↑ Стариков В. Н. 10-е исследование по геометрии (§ До- (пред-)- и пост-чевианы)// Научный рецензируемый электронный журнал МГАУ «Наука и образование». 2020. № 1. 7 с.// http://opusmgau.ru/index.php/see/article/view/ 1604
- ↑ Дмитрий Ефремов. Новая геометрия треугольника Архивная копия от 25 февраля 2020 на Wayback Machine. — Одесса, 1902. — С. 16.
Литература[править | править код]
- Ефремов Дм. Новая геометрия треугольника, 1902 год.
Медиана равна половине гипотенузы прямоугольного треугольника!
Почему??? При чём тут прямой угол?
Давай смотреть внимательно. Только не на треугольник, а на … прямоугольник.
Ты заметил, что наш треугольник ( displaystyle ABC) – ровно половина этого прямоугольника?
Проведём диагональ ( displaystyle BD):
Помнишь ли ты, что диагонали прямоугольника равны и делятся точкой пересечения пополам?
Если не помнишь, загляни в тему «Параллелограмм, прямоугольник, ромб…»
Но одна из диагоналей – ( displaystyle AC) – наша гипотенуза! Значит, точка пересечения диагоналей – середина гипотенузы ( displaystyle Delta ABC).
Она называлась у нас ( displaystyle M).
Значит, половина второй диагонали – наша медиана ( displaystyle BM). Диагонали равны, их половинки, конечно же, тоже. Вот и получим ( displaystyle BM=MA=MC)
Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы.
Более того, так бывает только в прямоугольном треугольнике!
Если медиана равна половине стороны, то треугольник прямоугольный, и эта медиана проведена к гипотенузе.
Доказывать это утверждение мы не будем, а чтобы в него поверить, подумай сам: разве бывает какой-нибудь другой параллелограмм с равными диагоналями, кроме прямоугольника?
Нет, конечно! Ну вот, значит, и медиана может равняться половине стороны только в прямоугольном треугольнике.
Решение задач на свойства медианы в прямоугольном треугольнике
Давай посмотрим, как это свойство помогает решать задачи.
Задача №1:
В ( displaystyle Delta ABC) стороны ( displaystyle AC=5); ( displaystyle BC=12). Из вершины ( displaystyle C) проведена медиана ( displaystyle CN).
Найти ( displaystyle AB), если ( displaystyle AB=2CN).
Рисуем:
Сразу вспоминаем, это если ( displaystyle CN=frac{AB}{2}), то ( displaystyle angle ACB=90{}^circ )!
Ура! Можно применить теорему Пифагора!
Видишь, как здорово? Если бы мы не знали, что медиана равна половине стороны только в прямоугольном треугольнике, мы никак не могли бы решить эту задачу. А теперь можем!
Применяем теорему Пифагора:
( A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}})
( A{{B}^{2}}={{5}^{2}}+{{12}^{2}}=169)
Ответ: ( AB=13)
А в следующей задаче пусть у нас будет не одна, а целых три медианы! Как же они себя ведут?
Запомни очень важный факт:
Три медианы в треугольнике (любом!) пересекаются в одной точке и делятся этой точкой в отношении ( 2:1), считая от вершины.
Сложно? Смотри на рисунок:
Медианы ( displaystyle AM), ( displaystyle BN) и ( displaystyle CK) пересекаются в одной точке.
Запомни:
- ( displaystyle AO) – вдвое больше, чем ( displaystyle OM);
- ( displaystyle BO) – вдвое больше, чем ( displaystyle ON);
- ( displaystyle CO) – вдвое больше, чем ( displaystyle OK).
Три медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении ( displaystyle 2:1 ), считая от вершины.
Что бы это такое значило? Посмотри на рисунок. На самом деле утверждений в этой теореме целых два. Ты это заметил?
1. Медианы треугольника пересекаются в одной точке.
2. Точкой пересечения медианы делятся в отношении ( displaystyle 2:1 ), считая от вершины.
Давай попробуем разгадать секрет этой теоремы, то есть доказать ее.
Доказательство теоремы о трех медианах треугольника
Сначала проведем не все три, а только две медианы. Они-то уж точно пересекутся, правда? Обозначим точку их пресечения буквой ( displaystyle E).
Соединим точки ( displaystyle N) и ( displaystyle K). Что получилось?
Конечно, ( displaystyle NK) – средняя линяя ( displaystyle triangle ABC). Ты помнишь, что это значит?
- ( displaystyle NK) параллельна ( displaystyle AC);
- ( displaystyle NK=frac{AC}{2}).
А теперь проведем ещё одну среднюю линию: отметим середину ( displaystyle AE) – поставим точку ( displaystyle F), отметим середину ( displaystyle EC) — поставим точку ( displaystyle G).
Теперь ( displaystyle FG) – средняя линия ( displaystyle triangle AEC). То есть:
- ( displaystyle FG) параллельна ( displaystyle AC);
- ( displaystyle FG=frac{AC}{2}).
Заметил совпадения? И ( displaystyle NK) , и ( displaystyle FG) – параллельны ( displaystyle AC). И ( displaystyle NK=frac{AC}{2}), и ( displaystyle FG=frac{AC}{2}).
Что из этого следует?
- ( displaystyle NK) параллельна ( displaystyle FG);
- ( displaystyle NK=FG)
Посмотри теперь на четырехугольник ( displaystyle NKGF). У какого четырехугольника противоположные стороны (( displaystyle NK) и ( displaystyle FG)) параллельны и равны?
Конечно же, только у параллелограмма!
Значит, ( displaystyle NKGF) – параллелограмм. Ну и что?
А давай вспомним свойства параллелограмма. Например, что тебе известно про диагонали параллелограмма? Правильно, они делятся точкой пересечения пополам.
Снова смотрим на рисунок.
Получилось что:
Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике по треугольникам
Лучше всего смотреть это видео с ручкой и тетрадкой в руках. То есть ставьте видео на паузу и решайте задачи самостоятельно.
Помните, понимать и уметь решать — это два, совершенно разных навыка. Очень часто вы понимаете как решить задачу, но не можете это сделать. Или допускаете ошибки, или просто теряетесь и не можете найти ход решения.
Как с этим справиться?
Нужно решать много задач. Другого способа нет. Вы должны совершить свои ошибки, чтобы научиться их не допускать.
ЕГЭ №6 Равнобедренный треугольник, произвольный треугольник
В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ. Очень часто все «проблемы» с решением задач на равнобедренный треугольник решаются построением высоты. Также мы научимся решать и «обычные» треугольники.
ЕГЭ №6 Прямоугольный треугольник, теорема Пифагора, тригонометрия
Большинство задач в планиметрии решается через прямоугольные треугольники. Как это так? Ведь далеко не в каждой задаче речь идёт о треугольниках вообще, не то что прямоугольных.
Но на уроках этой темы мы убедимся, что это действительно так. Дело в том, что редкая сложная задача решается какой-то одной теоремой — почти всегда она разбивается на несколько задач поменьше.
И в итоге мы имеем дело с треугольниками, зачастую — прямоугольными.
В этом видео мы научимся решать задачи о прямоугольных треугольниках из ЕГЭ, выучим все необходимые теоремы и затронем основы тригонометрии.
ЕГЭ №16. Подобие треугольников. Задачи н доказательство
Это одна из самых сложных задачи в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников!
Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства. Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.
В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.
Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.
Вы научитесь также применять подобие треугольников не только для доказательств, а и для расчётных задач.
Определение и свойства медианы треугольника
В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.
Определение медианы треугольника
Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.
Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).
Свойства медианы
Свойство 1 (основное)
Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.
В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:
Свойство 2
Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.
Свойство 3
Три медианы делят треугольник на 6 равновеликих треугольников.
Свойство 4
Наименьшая медиана соответствует большей стороне треугольника, и наоборот.
- AC – самая длинная сторона, следовательно, медиана BF – самая короткая.
- AB – самая короткая сторона, следовательно, медиана CD – самая длинная.
Свойство 5
Допустим, известны все стороны треугольника (примем их за a, b и c).
Длину медианы ma, проведенную к стороне a, можно найти по формуле:
Примеры задач
Задание 1
Площадь одной из фигур, образованной в результате пересечения трех медиан в треугольнике, равняется 5 см 2 . Найдите площадь треугольника.
Решение
Согласно свойству 3, рассмотренному выше, в результате пересечения трех медиан образуются 6 треугольников, равных по площади. Следовательно:
S△ = 5 см 2 ⋅ 6 = 30 см 2 .
Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.
Решение
Воспользуемся формулой, приведенной в свойстве 5:
Все формулы медианы треугольника
Медиана – отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M – медиана, отрезок |AO|
c – сторона на которую ложится медиана
a, b – стороны треугольника
γ – угол CAB
Формула длины медианы через три стороны, ( M ):
Формула длины медианы через две стороны и угол между ними, ( M ):
Медиана треугольника
Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).
Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.
На рисунке 1 медианой является отрезок BD .
Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).
Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),
и заметим, что (см. раздел нашего справочника «Площадь треугольника»)
Поскольку отрезок BD является медианой, то
что и требовалось доказать.
Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.
Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).
Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).
Теперь рассмотрим четырёхугольник FEDG (рис. 5).
Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,
Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,
Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.
Следствие . Все три медианы треугольника пересекаются в одной точке.
Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).
Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.
Определение . Точку пересечения медиан треугольника называют центроидом треугольника.
Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).
Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна 
[spoiler title=”источники:”]
http://www-formula.ru/mediantriangles
http://www.resolventa.ru/spr/planimetry/mediana.htm
[/spoiler]
Длина медианы треугольника
Воскресенье, 20 октября, 2019
Очень часто в ЕГЭ, ОГЭ и других экзаменах по математике встречаются задачи, в которых требуется найти длину медианы треугольника, если известны его стороны. Это действительно возможно, ведь длины трёх сторон треугольника полностью его определяют. В данной статье профессиональный репетитор по математике и физике объясняет, как это можно сделать.
Вопрос о том, как найти длину медианы треугольника, если известны все стороны треугольника, действительно имеет смысл. Ведь треугольник определяется длинами его сторон. То есть нет двух разных треугольников с одинаковыми сторонами. По третьему признаку равенства треугольников это должны быть два равных треугольника. Это означает, что если мы знаем все стороны в треугольнике, то мы можем найти в нём все основные элементы. В том числе и длины всех медиан. Разберёмся, как находится длина медианы треугольника.
Изобразим треугольник ABC. Обозначим его стороны маленькими буквами ,
и
, причём сторона
пусть лежит напротив угла A, сторона
— напротив угла B и сторона
— напротив угла C. Это стандартное обозначение, которое часть используется в учебниках по геометрии. Проведём также медиану AM, которая разделит сторону BC на два равных отрезка, длины которых составляют по
. Обозначим длину этой медианы
, имея в виду, что эта медиана проведена именно к стороне
:
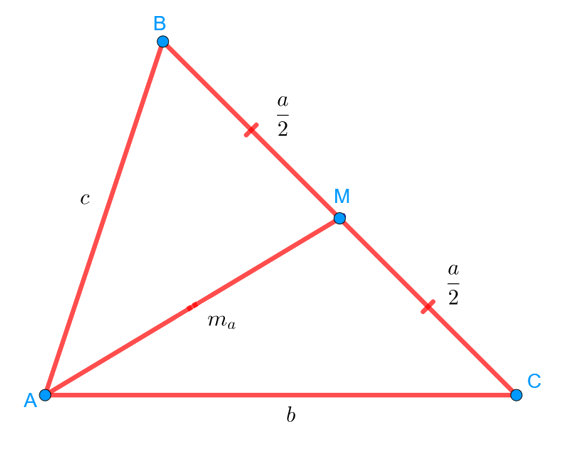
То есть — это длина медианы треугольника, которую нам нужно найти. Наша задача состоит в том, чтобы выразить её через длины сторон треугольника
,
и
.
Ну и идея состоит в том, чтобы использовать стандартное в таких случаях дополнительное построение, которое условно называют «удвоением медианы». Продлим медиану AM за точку M на отрезок MD, равный по длине медиане AM. То есть длина отрезка MD тоже равна . Как это нам поможет? Дело в том, что, соединив точку D c точками B и C, мы получаем четырёхугольник ABDC, который в действительности является параллелограммом:
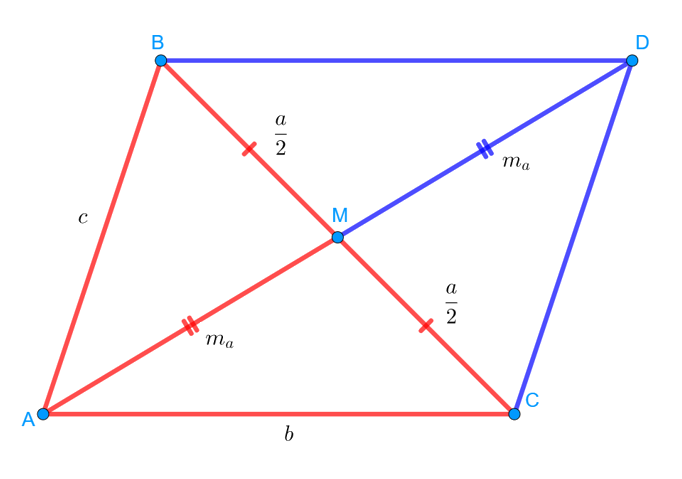
Естественно! Ведь есть такой признак. Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм. Здесь у нас получается ровно эта ситуация. M — середина AD, и одновременно — середина BC. Значит, ABDC — параллелограмм. Это означает, в частности, что BD = b, а DC = c, так как противоположные стороны параллелограмма равны.
Ну а дальше действовать можно по-разному. Но поскольку у всех всегда разный уровень знаний по геометрии, то я постараюсь обойтись в дальнейшем самыми известными фактами из геометрии. Я имею в виду теорему Пифагора. Я думаю, что вы все прекрасно её знаете. Ну или хотя бы про неё слышали.
Итак, проведём высоты нашего параллелограмма BF и DH. Обозначим длины этих высот буквой . А вот отрезочки AF и CH обозначим за
. Они будут одинаковые по длине, потому что равны прямоугольные треугольники ABF и CDH. Они, конечно же, равны, ведь у них равны гипотенузы AB и CD, а также катеты BF и DH:
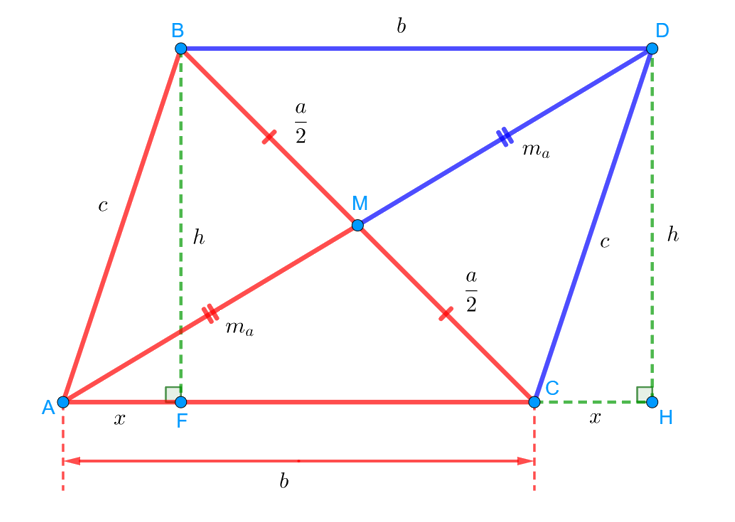
Ну а теперь рассмотрим прямоугольный треугольник BFC. Запишем для него теорему Пифагора:
(1)
Аналогично для прямоугольного треугольника ADH получаем по теореме Пифагора:
(2)
Ну и для прямоугольного треугольника ABF по теореме Пифагора получаем:
(3)
То есть получается три уравнения. Нужно их использовать, чтобы найти . Как же это сделать? Во-первых, сложим вместе уравнения (1) и (2), раскроем скобки и приведём подобные слагаемые. В результате получаем следующее выражение:
Ну и теперь осталось использовать уравнение (3), только сперва нужно умножить обе части этого уравнения на 2. Тогда получим, что . Ну и тогда мы получаем выражение
, из которого получаем окончательно:
Вот искомая формула, которую мы не просто записали, но ещё и доказали. Но ирония заключается в том, что запоминать её совсем не обязательно. Лучше просто знать, как её вывести, и получать её каждый раз при решении каждой конкретной задачи.
Задавайте свои вопросы по математике и физике в комментариях. Здесь на сайте и на моём Youtube-канале. На самые часто задаваемые вопросы я отвечу в следующих видео и статьях. Всего доброго!
Репетитор по математике и физике Сергей Валерьевич