Как найти длину медианы высоту через координаты

Аналитическая геометрия

Задача 3. Даны вершины треугольника ABC (рис. 1): А(-4,8), В(5,-4), С(10, 6).

1) длину стороны АВ;

2) уравнение высоты СД и ее длину;

3) уравнение медианы, проведенной из вершины А;

4) записать уравнение прямой, проходящей через точку С параллельно стороне АВ.

1. Расстояние d между точками М1(x1у1) и М2(х2у2) определя­ется по формуле

(1)

Подставим в формулу (1) координаты точек А и В, получим

.

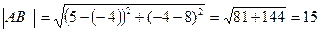2. Уравнение прямой, проходящей через точки М1(x1у1) и М2(х2у2), имеет вид

(2)

Подставив в формулу (2) координаты точек А и В, получим уравнение пря­мой АВ:

Для нахождения углового коэффициента КАВ прямой АВ разрешим полученное уравнение относительно у: .

Отсюда . Т. к. высота СD перпендикулярна АВ, то угловой коэффициент будет равен , .

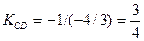Искомая высота проходит через точку С(10,6). Воспользуемся уравнением прямой, проходящей через данную точку, с заданным угловым коэффициентом:

Y-6= (x-10), 3x-4y-6=0 (СD)

Для нахождения длины СD определим координаты точки D, решив систему уравнений (АВ) и (СD): , откуда х=2, у=0, т. е. D(2,0).

Подставив в формулу (1) координаты точек С и Д, находим

3. Обозначим основание искомой медианы через М. По определению медианы М делит сторону ВС пополам. Координаты точки М най­дем по формуле

(4)

Чтобы записать уравнение медианы AM, воспользуемся форму­лой (2). , , , (АМ)

4. Обозначим искомую прямую СР. Угловой коэффициент , т. к. АВ и СР параллельны, то искомая прямая проходит через точку С (10,6). Воспользуемся уравнением (3)

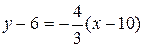, , (СP)

Задача 4. Расходы на автомобильном транспорте выражаются формулой у=120+30х, а на железнодорожном – у=160+20х, где х – расстояние в километрах, у – транспортные расходы на 1 км. (в усл. ден. ед.).

Построить графики функций, произвести экономический анализ, рассчитать транспортные расходы при х=200 км.

1. Построим прямые у=120+30х (I) и у=160+20х (II) (рис. 4).

Рис.4

Найдем точку пересечения двух прямых

х0=4 у0=240

Если х=4, оба вида транспорта эквивалентны по затратам.

Если х 4 выгоднее становятся же­лезнодорожные перевозки.

Рассчитаем транспортные расходы при х=200 км.
у=120+30∙200=6120 (усл. ден. ед.) – затраты на автомобильном

У=160+4000=4150 (усл. ден. ед.) – затраты на железнодорожном транспорте.

Примеры решений по аналитической геометрии на плоскости

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.

Решения задач о треугольнике онлайн

Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.

Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.

Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.

Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.

Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.

Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.

Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, – 4)$, $В(3, 0)$ и $С(0, 6)$.

Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.

Уравнение медианы треугольника

Как составить уравнение медианы треугольника по координатам его вершин?

Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:

1. Найти координаты середины отрезка по координатам его концов.
2. Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.

Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).

Найти уравнения медиан треугольника.

Обозначим середины сторон BC, AC, AB через A₁, B₁, C₁.

Уравнение медианы AA₁ будем искать в виде y=kx+b.

Найдём уравнение прямой, проходящей через точки A(3;1) и A₁(1,5;-5). Составляем и решаем систему уравнений:

Отсюда k= 4; b= -11.

Уравнение медианы AA₁: y=4x-11.

2) Аналогично, координаты точки B₁ — середины отрезка AC

Можно в уравнение y=kx+b подставить координаты точек B(6;-3) и B₁(0;-3) и найти k и b. Но так как ординаты обеих точек равны, уравнение медианы BB₁ можно найти ещё быстрее: y= -3.

3) Координаты точки C₁ — середины отрезка BC:

Отсюда уравнение медианы CC₁ : y=0,8x-4,6.

[spoiler title=”источники:”]

http://www.matburo.ru/ex_ag.php?p1=agtr

[/spoiler]

Решить треугольник Онлайн по координатам

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

1) Зная координаты вершин Можем узнать координаты вектора BC (2-3; -3-1) = BC(-1; -4)

Прямая проходящая через точку A должна идти коллинеарно вектору BC, то есть

(х-0) = k•(-1)

(y-4) = k•(-4)

откуда получаем -х=k и -y/4 +1 = k, приравниваем k

-x = -y/4 + 1 или

4x – y = -4

2) Медиана треугольника приходит в середину противоположной стороны. То есть в точку М – середина AС. Её координаты х = (0+2)/2 = 1; y = (4+(-3))/2 = 0,5; M(1; 0,5)

Получаем медиана идет из точки B в направлении вектора MB (3-1; 1-0,5) = MB (2; 0,5)

Получаем (x-3)/2 = (y-1)/0,5

0,5х – 1,5 = 2y – 2

x – 4y = -1

3) Высота из вершины С перпендикулярна стороне AB. То есть Вектора AB и CH ортогональны и их скалярное произведение = 0

AB (3-0; 1-4) = AB(3; -3)

CH (x-2; y-(-3))

<AB•СH> = 3•(х-2) + (-3)•(y+3) = 0

3x-6 – 3y – 9 = 0

x-y = 5 – получили уравнение прямой высоты CH

Уравнение прямой AB: (х-0)/3 = (y-4)/(-3)

x+y = 4

Точка Н – пересечение этих двух прямых:

Решая систему уравнений подстановкой, находим х=4,5; y=-0,5

CH (4,5-2; -0,5+3) = CH(2,5; 2,5)

|CH| = √(2,5² + 2,5²) = 2,5•√2

Ответ:

1) 4x – y = -4;

2) x – 4y = -1;

3) 2,5•√2