Длина отрезка. Расстояние между точками: онлайн-калькулятор
Чтобы найти расстояние между точками (длину отрезка) онлайн, необходимо:
- Задать размерность (плоскость или пространство).
- Ввести в поля координаты точек.
- Нажать «рассчитать».
Расстояние между точками онлайн
Для нахождения длины отрезка по координатам существует формула. Для отрезка AB в трехмерном пространстве она имеет вид:
d=xb-xa2+yb-ya2+zb-za2
Даже если вы забыли данную формулу, расстояние между точками всегда можно найти по координатам онлайн. Калькулятор не только предоставляет правильный ответ, но и подробно расписывает решение.
Онлайн-калькулятор нахождения длины отрезка по координатам будет полезен школьникам и студентам в самостоятельной подготовке, а также преподавателям и всем любителям математики.
тупое решение в лоб – идем в поисковик, и просто тупо пишем: расстояние между отрезками
вторая же ссылка (ну лично у меня) – Ю2.30. Расстояние между отрезками
там и описание и решение и код, правда на Си
берем его и переписываем на Python, получаем:
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import math
def ras (x1, y1, x2, y2, x3, y3):
## Если отрезок вертикальный - меняем местами координаты каждой точки.
if x1==x2:
x1, y1 = y1, x1
x2, y2 = y2, x2
x3, y3 = y3, x3
k=(y1-y2)/(x1-x2) ## Ищем коэффициенты уравнения прямой, которому принадлежит данный отрезок.
d=y1-k*x1
xz=(x3*x2-x3*x1+y2*y3-y1*y3+y1*d-y2*d)/(k*y2-k*y1+x2-x1)
dl=-1
if ( xz<=x2 and xz>=x1 ) or ( xz<=x1 and xz>=x2 ):
dl=math.sqrt((x3-xz)*(x3-xz)+(y3-xz*k-d)*(y3-xz*k-d)) ## Проверим лежит ли основание высоты на отрезке.
return dl
## Вводим параметры отрезков
# xa, ya, xb, yb = [1, 1, 2, 2]
# xc, yc, xd, yd = [2, 1, 3, 0]
xa, ya, xb, yb = [int(s) for s in input().split()]
xc, yc, xd, yd = [int(s) for s in input().split()]
min=-1
t=-2
s=-2
o=(xb-xa)*(-yd+yc)-(yb-ya)*(-xd+xc)
o1=(xb-xa)*(yc-ya)-(yb-ya)*(xc-xa)
o2=(-yd+yc)*(xc-xa)-(-xd+xc)*(yc-ya)
if o!=0:
t=o1/o
s=o2/o
if (t>=0 and s>=0) and (t<=1 and s<=1):
min=0 ## Проверим пересекаются ли отрезки.
else:
## Найдём наименьшую высоту опущенную из конца одного отрезка на другой.
dl1=ras(xa,ya,xb,yb,xc,yc)
min=dl1
dl2=ras(xa,ya,xb,yb,xd,yd)
if ( dl2<min and dl2!=-1 ) or min==-1 :
min=dl2
dl3=ras(xc,yc,xd,yd,xa,ya)
if ( dl3<min and dl3!=-1 ) or min==-1 :
min=dl3
dl4=ras(xc,yc,xd,yd,xb,yb)
if ( dl4<min and dl4!=-1) or min==-1 :
min=dl4
if min==-1 :
## В случае, если невозможно опустить высоту найдём минимальное расстояние между точками.
dl1=math.sqrt((xa-xc)*(xa-xc)+(ya-yc)*(ya-yc))
min=dl1
dl2=math.sqrt((xb-xd)*(xb-xd)+(yb-yd)*(yb-yd))
if dl2<min :
min=dl2
dl3=math.sqrt((xb-xc)*(xb-xc)+(yb-yc)*(yb-yc))
if dl3<min :
min=dl3
dl4=math.sqrt((xa-xd)*(xa-xd)+(ya-yd)*(ya-yd))
if dl4<min :
min=dl4
print (min)PS: ну, …. пробовали?? или нужно на подносе?
|
Отрезок, равный 40 см, разделён на четыре неравных отрезка. Расстояние между серединами крайних отрезков равно 28 см. Найдите расстояние между серединами средних отрезков в сантиметрах. А я, как обычно, через переменные и уравнения. Обозначим отрезки k, l, m, n, расположенные в таком порядке. k и n – крайние отрезки. Сумма длин всех отрезков равна 40 см. Получаем уравнение: k+l+m+n=40 (1) Расстояние между серединами крайних отрезков, равное 28 см, составляют половины крайних отрезков и 2 средних. Получаем такое уравнение: k/2+l+m+n/2=28 Домножим на 2, чтобы уйти от знаменателей. k+2l+2m+n=56 (2) Вычтем из (2) уравнения (1) уравнение. Получим: l+m=16 см – Это длина двух средних отрезков вместе, а нам нужно найти расстояние между их серединами, оно будет составлять половину этой длины двух отрезков, то есть: 16/2=8 см. Ответ: 8 см. автор вопроса выбрал этот ответ лучшим Лара Изюминка 6 месяцев назад Попробуем разобраться в задаче. Итак, известно, что весь отркзок 40. И состоит он из 4 неравных отрезков. ХУZW. Расстояние между серединами крайних отрезков известно, оно равно 28. Далее можно заметить, что 1/2хплюс у плюс z плюс 1/2 w равно 28. Тогда можем найти разницу между всем отрезком и этой известной его частью она будет равна 1/2х плюс 1/2 z=40-28=12. Тогда сумма отрезков крайних х и z будет равна в два раза больше, то есть 12*2=24. Тогда сумма средних отрезков равна 40-24=16. Тогда расстояние между их серединами будет равно их сумме поделенной на 2, то есть 16/2=8. Ответ на эту задачку 8.
Nasos 6 месяцев назад Поскольку расстояние между серединами крайних отрезков равно 28см, то по краям остаётся в сумме: 40см – 28см = 12см, а это не что иное, как половина суммы длины обоих крайних отрезков, следовательно, из суммарная длина равна 24см, а тогда на суммарную длину двух средних отрезков приходится: 40см – 24см = 16см, откуда не трудно посчитать, что расстояние между их серединами будет вдвое меньше, то есть 8см.
Грустный Роджер 6 месяцев назад Ну пусть расстояние от середины самого левого куска до левого конца отрезка х см. Тогда расстояние от середины самого правого куска до правого конца отрезка – 12-х см (12 – это 40-28). Значит, сумма длин двух крайних отрезков составляет 24 см. Тогда сумма длин двух средних – 16 см. И расстояние между их серединами – половина от этого, то есть 8 см. Знаете ответ? |
Смотрите также: Что такое равновеликие фигуры (куб, квадрат, многоугольник)? Для чего нужна математика, геометрия, физика в программировании? Как отложить на данном луче от его начала отрезок, равный данному? Как найти вписанный угол ACB, если дуга BC составляет 80 градусов? Как найти длину отрезка BD, если SO = 35, SD = 37? Как найти величину угла OAB, если угол OCD равен 30 градусам? По каким учебникам изучают математику израильские школьники? Как решить: В четырехугольнике АВСD противоположные стороны не параллельны? Диагональ АС параллелограмма АВСD 21, от верш. В до диаг. 12. Чему равна S? Как найти площадь треугольника ABM (см.)? |
Расстояния между двумя точками
На данной странице калькулятор поможет рассчитать расстояние между двумя точками онлайн в плоскости и пространстве. Для расчета задайте координаты.
Расстояние между двумя точками — это длина отрезка, которая соединяет эти точки.
Расстояния между двумя точками
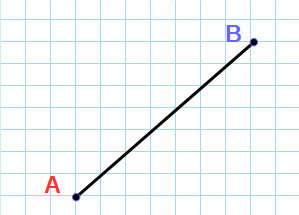
Формула вычисления расстояния между двумя точками A(xa; ya) и B(xb; yb) на плоскости:
Формула вычисления расстояния между двумя точками A(xa; ya; za) и B(xb; yb; zb) в пространстве:
Вывод формулы для вычисления расстояния между двумя точками на плоскости
Из точек A и B опустим перпендикуляры на оси координат x и y.
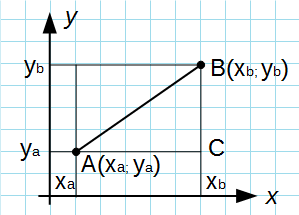
Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:
Спомощью теоремы Пифагора, вычислим длину отрезка AB:
Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.
Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.
Расстояние между отрезками
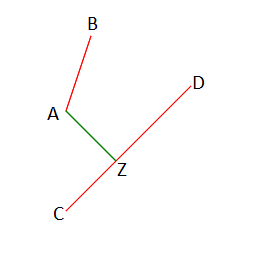
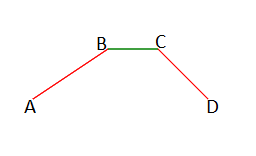
Координаты концов первого отрезка: A(xa, ya), B(xb, yb).
Координаты концов второго отрезка: C(xc, yc), D(xd, yd).
Тогда t = Δ1/Δ, s = Δ2/Δ. Если 0 ≤ t,s ≤ 1 и Δ ≠ 0, то отрезки пересекаются и расстояние между ними min равно 0, иначе с каждого конца отрезка попытаемся опустить высоту на противоположный. Если отрезок, на который опускаем высоту вертикальный, то поменяем местами координаты каждого конца отрезка и точки, с которой опускаем высоту (таким образом сохраним расстояние между точкой и отрезком, а отрезок станет горизонтальным).
Пусть k и d — коэффициенты уравнения прямой, на которую опущена эта высота. Основание высоты будет находится на прямой в точке Z, координаты Z(xz, yz) можно найти по формуле yz = kxz + d. Поскольку высота перпендикулярна отрезку — скалярное произведение их векторов равно 0. Тогда (x2 — x1)(x3 — xz)+(y2 — y1)(y3 — yz) = 0, соответственно xz = (x3x2 — x3x1 + y2y3 — y1y3 + y1d — y2d)/(ky2 — ky1 + x2 — x1), где (x3, y3) — координаты точки, с которой была опущена высота, (x1, y1) и (x2, y2) — координаты концов отрезка, принадлежащего прямой на которую опущена высота.
Вычислим длину dl каждой высоты, основание которой принадлежит одному из данных отрезков: dl = √((x3 — xz) 2 + (y3 — kxz — d) 2 ).
Минимальная длина высоты и будет наименьшим расстоянием между отрезками. В случае, если невозможно опустить высоты из одного отрезка на другой: расстояние между ними будет равно минимальному расстоянию между концами двух отрезков: min = √((x1 — x3) 2 + (y1 — y3) 2 ), где (x1, y1) — координаты одного из концов первого отрезка, а (x3, y3) — координаты одного из концов второго отрезка.
Отрезок. Формула длины отрезка.
Отрезком обозначают ограниченный двумя точками участок прямой. Точки – концы отрезка.
Общеизвестный факт, что каждая точка А плоскости имеет свои координаты (х, у).
В данном примере вектор AB задан координатами (х2— х1, y2— y1). Квадрат длины вектора будет равен сумме квадратов его координат. Следовательно, расстояние d между точками А и В, или, что то же самое, длина вектора АВ, вычисляется согласно формуле:
Эта формула длины отрезка предоставляет возможность рассчитывать расстояние между двумя произвольными точками плоскости, при условии, что известны координаты этих точек
Вышеуказанную формулу длины отрезка можно доказать и другим способом. В системе координат заданы координаты крайних точек отрезка координатами его концов(х1y1) и (х2,у2).
Прочертим прямые лини через эти точки перпендикулярно к осям координат, в результате имеем прямоугольный треугольник. Первоначальный отрезок является гипотенузой образовавшегося треугольника. Катеты треугольника сформированы отрезками, их длиной будет проекция гипотенузы на оси координат.
Установим длину этих проекций.
На ось у длина проекции равна y2 — y1, а на ось х длина проекции равна х2 — х1. На основании теоремы Пифагора видим, что |AB|² = (y2 – y1)² + (x2 – x1)².
В рассмотренном случае |AB| выступает длиной отрезка.
Вычислим длину отрезка АВ, для этого извлечем квадратный корень. Результатом является все та же формула длины отрезков по известным координатам конца и начала.
Эта информация доступна зарегистрированным пользователям
Начнем знакомство с одним из разделов математики, который называется геометрия.
Слово геометрия древнегреческого происхождения, оно означает «землемерие» («гео» – земля, «метрео» – измерять).
Геометрия – древняя наука, возникла в результате практической деятельности человека: строительства зданий и дорог, установления земельных наделов и определения их размеров.
Становление данной науки происходило тысячелетиями.
В настоящее время геометрия – наука, занимающаяся изучением геометрических фигур, их свойствами, размерами и преобразованиями.
Сегодня обратим внимание на основные, базовые геометрические фигуры, такие как точка и отрезок.
Эта информация доступна зарегистрированным пользователям
Узнаем, что называют ломаной линией, какие геометрические фигуры называют многоугольниками, рассмотрим их основные элементы и характеристики.
Научимся сравнивать, находить длины отрезков.
Познакомимся с различными единицами измерения отрезков.
Рассмотрим свойства измерения длин отрезков.
Геометрическая фигура- это математическая модель, в которой рассматривается только форма и размер, не обращая внимания на иные свойства и состояния (цвет, из какого материала изготовлены, в каком состоянии находятся).
Как здания складываются из кирпичиков, так и сложные геометрические фигуры состоят из базовых фигур.
Одной такой элементарной фигурой является точка.
Точка – это неделимая фигура, не имеет частей и размеров (высоты, радиуса, длины и т.д.), направления и других характеристик.
В реальности моделью, которая дает представление о точке может стать, например, след, оставленный острием карандаша, или отверстие на бумаге от швейной иглы.
Эта информация доступна зарегистрированным пользователям
Слово «точка» с латинского языка означает мгновенное касание, укол.
Точку принято рассматривать как некоторое место в пространстве или на плоскости.
Принято обозначать точки заглавными латинскими буквами (А, В, С и т.д.).
Две точки на плоскости можно соединить бесконечным множеством линий.
Эта информация доступна зарегистрированным пользователям
Самой короткой линией, соединяющей две точки на плоскости, будет прямая, проведенная по линейке через эти две точки.
Кратчайшая линия между двумя точками называется отрезком.
Любые две точки можно соединить только одним отрезком.
Эта информация доступна зарегистрированным пользователям
Отрезок – это часть прямой линии, ограниченной двумя точками.
Точки, ограничивающие отрезок, называются концами отрезка.
Отрезок обозначают указанием имен его концов.
Рассмотрим пример:
Через точки А и В с помощью линейки провели прямую.
Эта информация доступна зарегистрированным пользователям
А и В – концы отрезка.
Так как отрезок обозначают именами точек, получим отрезок АВ или ВА.
Пишут и говорят так: «Отрезок АВ» или «Отрезок ВА».
В названии отрезка не важно в каком порядке указываются его концы.
Отрезок АВ и ВА – это один и тот же отрезок.
Отрезок можно построить с помощью линейки.
Для этого необходимо к отмеченным на плоскости точкам приложить линейку и провести прямую от одного конца отрезка до другого.
Чтобы с помощью линейки начертить отрезок, который длиннее чем сама линейка, нужно поступить следующим образом:
Между точками А и В отметить точку С.
Эта информация доступна зарегистрированным пользователям
Затем передвинем линейку так, чтобы левый конец линейки оказался около точки С, по правому концу линейки отложим точку D.
Эта информация доступна зарегистрированным пользователям
Последовательно соединив концы отрезков, получится отрезок AD, который длиннее, чем линейка.
Эта информация доступна зарегистрированным пользователям
Каждый отрезок имеет определенную длину, значение которой является числом.
Длина в геометрии – это величина, которая характеризует протяженность.
Длина отрезка – это расстояние между концами отрезка.
Так как каждый отрезок имеет длину, отрезки можно измерять и сравнивать.
Существует несколько способов сравнения отрезков.
1. Приблизительный способ сравнения.
Данный способ сравнения применяют только в том случае, когда длины отрезков явно отличаются.
Пример: Даны два отрезка АВ и ЕР
Эта информация доступна зарегистрированным пользователям
Очевидно, что отрезок АВ длиннее отрезка ЕР, значит, АВ > ЕР
2. Совмещение отрезков – более точный способ сравнения отрезков.
Метод заключается в следующем: совмещаются два отрезка друг с другом так, чтобы совпали их концы с одной стороны.
По расположению других концов относительно друг друга можно оценить какой из отрезков длиннее, а какой короче.
Если при наложении отрезков друг на друга длины отрезков совпадут, то отрезки равны (отрезки в этом случае будут равными фигурами).
Если при наложении отрезков друг на друга один из отрезков будет составлять часть второго, то первый отрезок является короче второго (т.е. длина первого меньше длины второго).
Пример: Даны два отрезка АВ и ОЕ
Эта информация доступна зарегистрированным пользователям
Сравним данные отрезки методом совмещения отрезков.
Совместим левый конец А отрезка АВ и левый конец О отрезка ОЕ.
Эта информация доступна зарегистрированным пользователям
Можно заметить, что отрезок ОЕ составляет часть отрезка АВ.
Значит, отрезок ОЕ короче отрезка АВ.
Данный метод удобен, если есть возможность перемещать отрезки, совмещать один с другим.
3. Сравнение отрезков с помощью измерителя.
Если нет возможности перемещать сравниваемые отрезки, то можно использовать промежуточный измеритель.
В математике для этих целей используют специальный чертежный инструмент, который называется циркулем.
Эта информация доступна зарегистрированным пользователям
Чтобы сравнить отрезки с помощью циркуля, необходимо совместить концы отрезка с ножками циркуля.
Не меняя раствор циркуля, приложить его ко второму отрезку и сравнить.
- Если ножки циркуля совпадают с концами сравниваемого отрезка, то отрезки считаются равными.
- Если отрезок выходит за пределы расставленных ножек циркуля, то он больше исходного отрезка.
- Если же отрезок находится между концами измерителя, то сравниваемый отрезок меньше исходного.
Если нет возможности сравнить отрезки наложением и нет циркуля под рукой, то в качестве измерителя можно использовать нитку.
В таком случае нужно нитку приложить к исходному отрезку, на нитке по отрезку сделать замер, затем нитку приложить ко второму отрезку, оценить расположение замера на нитке по отношению к исследуемому отрезку, сделать вывод.
Пример:
Пусть даны три отрезка СD, АЕ, BG
Эта информация доступна зарегистрированным пользователям
Сравним эти отрезки с помощью циркуля.
Соединим ножки циркуля с концами С и D отрезка СD.
Приложим циркуль с заданным раствором к отрезку АЕ.
Концы измерителя совпали с точками отрезка АЕ, значит, отрезки CD и AE равны: (CD = AE).
Приложим циркуль с заданным раствором к отрезку BG.
Отрезок выходит за концы измерителя, т.е. является частью отрезка BG, следовательно, отрезок BG длиннее отрезка СD: (BG > СD).
Все рассмотренные способы сравнения длины отрезков проводят без определения значения длины сравниваемых отрезков.
4. Существует еще один способ сравнения длины отрезков путем измерения их длинны.
Для этого необходимо сначала измерить длину каждого отрезка, далее сравнить полученные значения их длины и сделать вывод.
Большим будет являться тот отрезок, длина которого больше.
Соответственно, если длины измеряемых отрезков равны, то и отрезки равны.
Эта информация доступна зарегистрированным пользователям
Многоугольником называется фигура, ограниченная замкнутой ломаной линией, звенья которой не пересекаются.
Отрезки (звенья) ломаной линии называют сторонами многоугольника.
Общие точки двух отрезков (сторон) многоугольника называют его вершинами.
Каждая пара сторон многоугольника, сходящиеся в одной точке, образуют углы многоугольника.
Количество сторон и количество углов в многоугольнике совпадают.
Вершины, стороны и углы многоугольника обозначаются аналогично ломаной линии.
Многоугольник принято обозначать и называть по его вершинам, начиная с любой вершины и называя их последовательно, в любом порядке.
Рассмотрим пример:
На рисунке изображен многоугольник АBCDEF.
Эта информация доступна зарегистрированным пользователям
Вершины многоугольника АBCDEF: А, B, C, D, Е, F.
Стороны многоугольника АBCDEF: AB, BC, CD, DE, EF, FA.
Любые многоугольники можно сравнить: два многоугольника называются равными, если они совпадают при наложении.
Зная длину каждой стороны многоугольника, можно найти периметр этого многоугольника.
Периметр многоугольника – это сумма длин всех сторон.
Периметр многоугольника принято обозначать заглавной латинской буквой Р
Найдем периметр многоугольника АBCDEF (изображенного на рисунке):
РАВСDEF = AB+ BC+ CD+ DE+ EF+ FA = 2 см + 3 см + 2 см + 2 см + 3 см + 2 см = 14 см.
Существует огромное множество различных видов многоугольников.
Обычно многоугольники различают по числу сторон и углов.
Например: пятиугольник имеет 5 углов и 5 сторон, шестиугольник – 6 углов и 6 сторон.
Многоугольник с наименьшим числом вершин, сторон и углов называют треугольником.
Треугольник – плоская геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих эти точки.
Треугольник часто обозначают символом «Δ» и тремя заглавными латинскими буквами, которые обозначают его вершины.
Рассмотрим пример:
Эта информация доступна зарегистрированным пользователям
На рисунке изображен треугольник АBC (Δ АBC).
А, В, С – вершины треугольника АBC.
Отрезки AB, BC, АC– стороны треугольника АBC.
Периметр треугольника- это сумма длин трех его сторон.
Найдем периметр треугольника АBC (изображенного на рисунке):
РАВС = AB+ BC+ АС = 4 см + 6 см + 3 см = 13 см.
Эта информация доступна зарегистрированным пользователям
В действительности часто приходится иметь дело с различными реальными объектами, а не с отрезками.
Говоря о ширине, высоте, толщине и т.д., мы имеем в виду длину какого-либо отрезка.
Давайте разберемся, что значит найти длину отрезка.
Измерить отрезок – значит найти его длину, т.е. определить расстояние между концами этого отрезка.
Для измерения длины отрезков применяют различные измерительные инструменты, сантиметровая линейка является простейшим из них.
По краю такой линейки нанесены деления (шкала), обозначающие сантиметры и их десятые части- миллиметры, что позволяет количественно оценить длину.
Чтобы измерить длину отрезка, необходимо:
- Приложить край линейки к отрезку
- Нулевую отметку шкалы делений линейки совместить с левым концом отрезка
- Результат измерения определить по шкале линейки: деление, которое совпадет с правым концом отрезка, будет означать длину отрезка
Рассмотрим пример:
Дан отрезок АВ.
Измерим его длину сантиметровой линейкой.
Эта информация доступна зарегистрированным пользователям
Нулевую точку шкалы линейки совместим с концом А отрезка АВ.
При этом конец В совпадет с делением шкалы линейки 4 см, значит, длина отрезка АВ равна 4 см. (АВ = 4 см.)
Этот способ измерение длины отрезка основан на сравнении этого отрезка с отрезком, длина которого принимается равной единице (единичным отрезком).
Измерить отрезок – это значит подсчитать сколько единичных отрезков содержится в нем.
Если за единичный отрезок, например, принять сантиметр, то для определения длины заданного отрезка необходимо узнать, сколько раз в данном отрезке помещается сантиметров.
Рассмотрим пример:
Эта информация доступна зарегистрированным пользователям
На рисунке изображены три отрезка.
Отрезок ОЕ– единичный отрезок = 1 см.
В отрезке АВ единичный отрезок ОЕ помещается 3 раза, в отрезке CD– 5 раз.
Это значит, что длина отрезка АВ = 3 единичных отрезка = 3 см. (говорят: «Отрезок АВ равен 3 см»).
Длина отрезка СD = 5 единичных отрезков = 5 см. (говорят: «Отрезок СD равен 5 см»).
Конечно, возможна ситуация, когда отрезок, принятый за единицу измерения, укладывается нецелое число раз в измеряемом отрезке, т.е. получается остаток.
В таком случае единичный отрезок (сантиметр в нашем случае) делят на десять равных частей (миллиметры) и определяют сколько в остатке измеряемого отрезка укладывается этих маленьких делений- миллиметров.
Эта информация доступна зарегистрированным пользователям
Разберемся, что называют суммой и разностью отрезков.
Задача 1
Пусть даны два отрезка СD = 5 см и АВ = 3 см.
Эта информация доступна зарегистрированным пользователям
Найдите сумму СD+АВ = ?
Решение:
Чтобы найти сумму отрезков СD и АВ, нужно расположить данные отрезки последовательно друг за другом, длина полученного отрезка будет являться суммой двух данных.
Эта информация доступна зарегистрированным пользователям
СD+ АВ = 5 см + 3 см = 8(см) сумма отрезков АВ и СD
Ответ: 8 (см)
Вывод: чтобы найти сумму отрезков, нужно сложить их длины.
Задача 2
Пусть даны два отрезка АВ = 5 см и СD = 3 см.
Эта информация доступна зарегистрированным пользователям
Найдите разность АВ – СD = ?
Решение:
Чтобы найти разность отрезков АВ и СD, нужно от левого конца большего отрезка отложить длину меньшего отрезка.
Длина отрезка, расположенного между правыми концами первого и второго отрезка, будет разностью двух исходных отрезков.
Эта информация доступна зарегистрированным пользователям
АВ – СD = 5 см – 3 см = 2(см) разность отрезков АВ и СD
Ответ: 2 (см)
Вывод: чтобы найти разность двух отрезков, нужно из длины большего отрезка вычесть длину меньшего.
Задача 3
Точка С– середина отрезка АВ.
Отрезок АВ равен 1 м 42 см.
Найдите длину отрезка АС и выразите ее в сантиметрах.
Точка С принадлежит отрезку AB и делит его на равные части, значит:
АС = СВ
1м = 100 см
АВ = 1 м 42 см = 142 см
Чтобы найти середину отрезка, нужно его длину разделить на два.
АС = СВ = АВ ÷ 2 = 142 ÷ 2 = 71 (см) длина отрезка АС
Ответ: 71 (см).
Эта информация доступна зарегистрированным пользователям
Геометрические иллюзии и обман зрения
Иллюзией называют неправильное, искаженное восприятие реальной картины мира.
Существуют различные иллюзии: слуховые, осязательные, иллюзии движения, иллюзии-перевертыши и т.д.
Геометрическая иллюзия- это оптический обман нашего мозга, который выражается в том, что видимые отношения элементов фигур не совпадают с фактическими.
Рассмотрим некоторые иллюзии связанны с искажением зрительного восприятия: иллюзии размера и контраста.
1. Иллюзия Болдуина.
Предмет кажется больше его реальной величины благодаря соседству с крупными объектами.
Эта информация доступна зарегистрированным пользователям
Отрезки №1 и №2 абсолютно равны.
2. Иллюзия Франца Мюллера-Лайера.
Стрелки и окружности на концах отрезков создают иллюзию искажения длины.
Происходит перенесения свойств целой фигуры на ее отдельные части.
Эта информация доступна зарегистрированным пользователям
Равные по длине отрезки воспринимаются неодинаковыми.
3. Иллюзия железнодорожных путей.
Верхний голубой отрезок кажется длиннее, но на самом деле оба отрезка имеют равную длину.
Эта информация доступна зарегистрированным пользователям
4. Отрезки АВ и СD равны
Эта информация доступна зарегистрированным пользователям
5. Иллюзия кинескопа.
Окна на картинке одинакового размера
Эта информация доступна зарегистрированным пользователям
6. Вертикально-горизонтальная иллюзия.
Эта информация доступна зарегистрированным пользователям
Линия №1 воспринимается длиннее линии №2.
