-
Построение коммуникационной сети минимальной длины
Коммуникационная
сеть минимальной длины
(или дерево
кратчайших расстояний)
– это совокупность дуг сети, имеющая
минимальную суммарную длину и
обеспечивающая достижение всех узлов
сети, т.е. возможность попасть из любого
узла в любой другой узел.
Алгоритм:
-
Начать
с любого узла и соединить его с ближайшим
узлом. Считаем, что эти узлы связанные,
а все другие несвязанные. -
Определить
несвязанный узел, ближайший к одному
из связанных узлов. Если таких «ближайших»
узлов несколько, то выбрать любой.
Добавить этот узел к связанным. И т.д.,
до тех пор, пока есть несвязанные узлы.
Пример.
Университет устанавливает компьютерную
систему электронной почты, которая
позволит передавать сообщения между
деканами восьми факультетов. Сеть
возможных электронных связей между
деканатами показана ниже. Протяженность
коммуникаций в километрах отмечена на
дугах.
Необходимо
предложить проект системы связи, которая
позволит всем восьми деканам обеспечить
доступ к системе электронной почты.
Решение должно обеспечить минимальную
возможную общую длину коммуникаций.

Длина
коммуникаций равна сумме расстояний
на дугах:
-
Задача определения кратчайшего пути Метод присвоения меток
Задача
состоит в том, чтобы найти кратчайший
путь на графе от какой-то выделенной
вершины до любой другой вершины.
Пример:
Узел 7 – склад, остальные узлы –
строительные площадки компании.
Показатели на дугах – расстояния в
километрах.
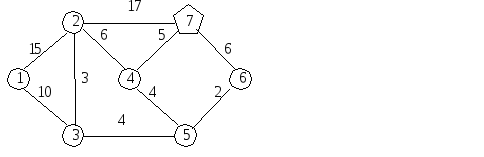
Надо
найти кратчайшие расстояния от склада
до каждой строительной площадки.
Каждому
узлу приписывают метку из двух чисел:
-
первое
число – минимальное расстояние от узла
7 до данного узла, -
второе
– номер предыдущего узла на пути от
узла 7 к данному узлу.
Помеченным
называют узел, для которого определен
путь от узла 7. Иначе узел – непомеченный.
Если
кратчайшее расстояние от узла 7 до
данного узла определено, то соответствующая
метка постоянная
и обозначается в круглых скобках.
Остальные метки временные
и обозначаются в квадратных скобках.
Узлы с постоянными метками закрашиваем.
Узлу
7 присваиваем метку (0, S), где 0 – расстояние
от узла 7, S – обозначение стартового
узла.
Узел
7 связан с узлами …. Им присваиваем
соответствующие метки –
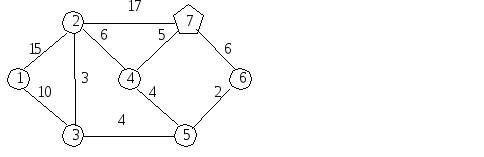
После
выполнения этой операции выполняют два
шага:
-
находят
участок минимальной длины и соответствующую
временную метку делают постоянной; -
узел,
которому соответствует данная постоянная
метка становится новым стартом.
Метка
с наименьшим расстоянием
соответствует узлу …. Этот узел объявляем
помеченным и заменяем скобки у метки.
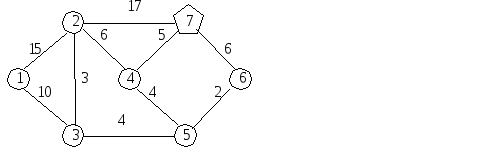
Узел
… связан непосредственно с узлами
без постоянных меток. Временная
метка узла … равна [ ]=[ ], а
у узла … – [ ]= [ ]. Т.к. узел
… уже имеет временную метку [ ], то
из двух меток выбираем ту, в которой
расстояние меньше, т.е. [
].
Из
всех временных меток [ ], [
], [ ] выбираем метку с наименьшим
первым числом – [ ]. Она становится
постоянной и очередной шаг начинаем с
узла ….
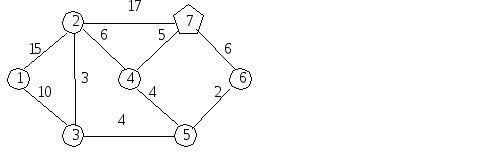
Этот
узел связан только с узлом … без
постоянной метки. Временная метка узла
… равна [ ]=[ ]. Эта метка имеет
меньшее первое число, чем предыдущая,
поэтому узлу … приписываем новую
временную метку [ ].
Из
всех временных меток [ ], [
] метку с наименьшим первым числом [
] объявляем постоянной и следующий шаг
начинаем с соответствующего ей узла ….
Узел
… связан только с одним узлом без
постоянной метки – узлом …. Временная
метка узла … равна [ ]=[ ].
Из
всех временных меток [ ], [
] метку с наименьшим первым числом [
] объявляем постоянной и следующий
шаг начинаем с соответствующего ей узла
…
Узел
… связан с узлами без постоянных
меток. Временная метка узла … равна [
]=[ ], а узла … – [ ]=[ ].
Т.к. узел … уже помечен меткой с меньшим
первым числом, то метку не меняем.
Из
временных меток [ ], [ ] метка с
наименьшим первым числом [ ] становится
постоянной и следующий шаг начинаем с
соответствующего ей узла ….
Метку
узла … меняем на ( )=( ).
Всем
узлам приписаны постоянные метки.
Действие алгоритма прекращается.
Первое
число метки у каждой вершины – это длина
кратчайшего пути от узла 7 до данной
вершины. Чтобы восстановить кратчайший
путь от узла 7 до какой-то вершины, нужно
из этой вершины перейти в соседнюю (ее
номер – второе число метки) и т.д. до
вершины 7.
Определим
кратчайшие расстояния от склада до
каждой строительной площадки:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
 Определить минимальную длину строки в массиве строк
Определить минимальную длину строки в массиве строк
Написать программу, которая возвращает минимальную длину строки в массиве строк (через функцию). .
Определить минимальную длину последовательности ненулевых элементов массива
Задан массив четырехбайтовых чисел, содержащий нулевые элементы. Определить минимальную длину.
Выбор кабеля для сети
Здравстуйте. очень нужна ваша помощь! в общем задача следующая, нужно проложить ,ЛВС из одного.
 Даны три отрезка координатами своих вершин. Определить общую длину этих отрезков
Даны три отрезка координатами своих вершин. Определить общую длину этих отрезков
Даны три отрезка координатами своих вершин. Определить общую длину этих отрезков, используя.
Итак, я ничего не понял и щас будем тупить в двоем 
Короче, тебе нужно для начала построить граф, A — количество вершин и B — количество ребер
И теперь (вроде бы, неточна о-чень) запускаем туда поиск минимального остовного дерева
Тут можно взять Краскала или Прима
Вот, например можно про Прима почитать тут, все расписано http://e-maxx.ru/algo/mst_prim
Добавлено через 2 минуты
Предупреждаю,что там какой-то косяк в реализации, если сам по описанию алгоритм составить не сможешь, посмотрю завтра че там исправить надо
Заказываю контрольные, курсовые, дипломные и любые другие студенческие работы здесь.
Выбор кабеля для локальной сети
Добрый день! Живу в частном секторе, от меня до ближайшего жилого дома 150метров, хочу подключить.
У меня есть связки объектов разного размера ( множество объектов может иметь одинаковый размер, например: у меня есть 54 объекта 6B, 76 из 10B, 79 из 24B и т. д.
Размер объектов — 6, 8, 10 . байты ). Мне нужно упаковать этот bundle в пару сообщений ( каждое сообщение имеет максимальную длину 256 байт).
Проблема в том, как получить решение с минимальным количеством сообщений?
Есть ли известный алгоритм для этого? Нужна ли мне нейронная сеть Хопфилда для этого?
3 ответа
- Нахождение минимальной длины нескольких списков
У меня есть три списка разной длины. Например List1 is of length 40 List2 is of length 42 List3 is of length 47 Как я могу использовать Python встроенный min() или любой другой метод, чтобы найти список с минимальной длиной? Я пытался: min(len([List1,List2,List3])) но я получаю TypeError: ‘int’.
Я пытаюсь реализовать Ограничение минимальной длины в Oracle. Как я прочитал в этом ответе и нескольких других подобных вопросах я попытался: ALTER TABLE my_table ADD CONSTRAINT MY_TABLE_PASSWORD_CK CHECK (DATALENGTH(password) >=4) И я получаю DATALENGTH: invalid identifier . Я тоже пытался: (.
Это пример задачи упаковки бункера, которая является комбинаторной NP-жесткой проблемой . Самый простой алгоритм-«First Fit Decreasing (FFD)», в котором сначала вы сортируете объекты по уменьшению размера, а затем вставляете каждый объект в первое сообщение в списке с достаточным оставшимся пространством.
Это своего рода проблема рюкзака, но не проблема рюкзака. Это проблема упаковки бункеров, в которой предметы разных объемов упаковываются в минимальное количество бункеров, которые имеют одинаковый размер. Это NP-трудно.
Первый алгоритм уменьшения подгонки (FFD) не является оптимальным (но очень хорошим началом). Если у вас больше времени на выполнение и больше времени на разработку , соедините его с имитацией отжига , поиском табу или генетическими алгоритмами . Игнорируйте грубую силу или ветвление и привязку : они не масштабируются за пределами проблемы игрушек.
- подстрока минимальной длины, которая отсутствует в файле
Я застрял на этом вопросе интервью : Дан файл из N байт. Найдите подстроку минимальной длины, которая отсутствует в файле. Есть идеи? спасибо.
Я пытаюсь создать ключ разблокировки, например XXXX-XXXX-XXXX или просто строку небольшой длины или шестнадцатеричную строку. Я использую алгоритм RSA для шифрования и расшифровки ключа. Я получил некоторые длинные строки, как.
Похожие вопросы:
я использую следующую функцию C#, чтобы получить набор полномочий, ограниченный подмножествами минимальной длины string[] PowerSet(int min_len, string set) <.
Метод добавления пустого пространства после проверки минимальной длины строки, если строка enter не равна определенной минимальной длине, а затем добавить пустое пространство после строки, чтобы.
Учитывая последовательность, такую как S = <1,8,2,1,4,1,2,9,1,8,4>, мне нужно найти подпоследовательность минимальной длины, которая содержит все элементы S (никаких дубликатов, порядок не имеет.
У меня есть три списка разной длины. Например List1 is of length 40 List2 is of length 42 List3 is of length 47 Как я могу использовать Python встроенный min() или любой другой метод, чтобы найти.
Я пытаюсь реализовать Ограничение минимальной длины в Oracle. Как я прочитал в этом ответе и нескольких других подобных вопросах я попытался: ALTER TABLE my_table ADD CONSTRAINT MY_TABLE_PASSWORD_CK.
Я застрял на этом вопросе интервью : Дан файл из N байт. Найдите подстроку минимальной длины, которая отсутствует в файле. Есть идеи? спасибо.
Я пытаюсь создать ключ разблокировки, например XXXX-XXXX-XXXX или просто строку небольшой длины или шестнадцатеричную строку. Я использую алгоритм RSA для шифрования и расшифровки ключа. Я получил.
Плагин Select2 Jquery У меня было трудное время, как переопределить сообщение по умолчанию для ввода минимальной длины в jquery Select2. по умолчанию плагин выдает следующее сообщение. текст по.
Я хочу решить проблему UVA 10298 — силовые строки , используя алгоритм KMP. В этом блоге показана методика использования функции отказа для вычисления минимальной длины повторяющейся подстроки.
У меня есть две строки: строка1 — hello how are you , Строка2 — olo (включая пробел) Выход: lo ho ( Хел Ло Хо ж ты ) lo ho -единственная подстрока, содержащая все символы string2. Может ли кто -.
Часто в задачах встречается следующая конструкция — есть дома и дороги, их соединяющие; у каждой дороги есть длина. По другой терминологии такая конструкция называется графом, дома называются «вершинами», дороги — «ребрами» или «дугами», а длина дороги «весом ребра» или «весом дуги». Таким образом фраза ‘Найти минимальный вес пути между вершинами s и k в графе’ может быть переведена так: ‘Есть дома и дороги их соединяющие. Также заданы длины дорог. Найти кратчайшую длину пути от города s до города k, если двигаться можно только по дорогам’. Пропускная способность дуги (i,j) означает, например, сколько груза может быть перевезено по дороге (по дуге) (i,j) за единицу времени); а поток по дуге (i,j) — это сколько перевозится сейчас на самом деле).
Часто используют следующие обозначения: Г(x(i))- множество вершин, в которые есть дуга из вершины i; Д(x(i))- множество вершин, из которых есть дуга в вершину i.
Пусть в графе N вершин.
Длины дуг обычно заносятся в матрицу (назовем ее C) размера N на N, называемой матрицей смежности:
var С: array [1..N,1..N] of integer;
Элемент C[i,j] этой матрицы равен длине дуги (дороги>), соединяющей вершины i и j, и равен (например) 0 или -1, если такой дуги нет. Если дорога двунаправленная (дуга неориентированная), то очевидно, что C[i,j]=C[j,i].
Алгоритм расстановки пометок для задачи о максимальном (от s к t) потоке.
А. Расстановка пометок. Вершина может находиться в одном из трех состояний: вершине приписана пометка и вершина просмотрена ( т.е. она имеет пометку и все смежные с ней вершины «обработаны»), пометка приписана, но вершина не просмотрена ( т.е. она имеет пометку, но не все смежные с ней вершины обработаны), вершина не имеет пометки. Пометка произвольной вершины x(i) состоит из двух частей и имеет один из двух видов: (+x(j),m) или (-x(j),m). Часть +x(j) пометки первого типа означает, что поток допускает увеличение вдоль дуги (x(j),x(i)). Часть -x(j) пометки другого типа означает, что поток может быть уменьшен вдоль дуги (x(i),x(j)). В обоих случаях m задает максимальную величину дополнительного потока, который может протекать от s к x(i) вдоль построенной увеличивающей цепи потока. Присвоение пометки вершине x(i) соответствует нахождению увеличивающей цепи потока от s к x(i). Сначала все вершины не имеют пометок.
- Шаг 1. Присвоить вершине s пометку (+s,m(s)=бесконечность). Вершине s присвоена пометка и она просмотрена, все остальные вершины без пометок.
- Шаг 2. Взять некоторую непросмотренную вершину с пометкой; пусть ее пометка будет (+-x(k),m(x(i))) (+- обозначает, что перед x(k) может стоять как плюс, так и минус).
(I) Каждой помеченной вершине x(j), принадлежащей Г(x(i)), для которой c(i,j) 0, присвоить пометку (-x(i),m(x(j))), где
(Теперь вершина x(i) и помечена, и просмотрена, а вершины x(j), пометки которым присвоены в (I) и (II), являются непросмотренными.) Обозначить каким-либо способом, что вершина x(i) просмотрена.
- Шаг 3. Повторять шаг 2 до тех пор, пока либо вершина t будет помечена, и тогда перейти к шагу 4, либо t будет не помечена и никаких других пометок нельзя будет расставить; в этом случае алгоритм заканчивает работу с максимальным вектором потока c. Здесь следует отметить, что если X(0)-множество помеченных вершин, а X'(0) — множество не помеченных, то ( X(0) —> X'(0) ) является минимальным разрезом.
Б. Увеличение потока.
- Шаг 4. Положить x=t и перейти к шагу 5.
- Шаг 5. (I) Если пометка в вершине x имеет вид (+z,m(x)), то изменить поток вдоль дуги (z,x) c c(z,x) на c(z,x)+m(t). (II) Если пометка в вершине x имеет вид (-x,z) c c(x,z) на c(x,z)-m(t).
- Шаг 6. Если z=s, то стереть все пометки и вернуться к шагу 1, чтобы начать расставлять пометки, но используя уже улучшенный поток, найденный на шаге 5. Если z<>s, то взять x=z и вернуть к шагу 5.
Обозначения: Г(x(i))- множество вершин, в которые есть дуга из вершины i; Д(x(i))- множество вершин, из которых есть дуга в вершину i; c(i,j) — это пропускная способность дуги (т.е., например, сколько груза может быть перевезено по дороге (по дуге) (i,j) за единицу времени); q(i,j) — поток по дуге (i,j) (т.е. сколько перевозится сейчас на самом деле).
Кратчайшее расстояние от вершины нач до остальных вершин.
C[i,j]- длина ребра(i,j), С[i,j]>=0 (если ребра нет, то его длина полагается равной бесконечности).
D[i]- кратчайшее текущее расстояние от вершины нач до вершины i.
флаг[i]- информация о просмотре вершины i: 0 — если вершина не просмотрена, 1 — если просмотрена. Если вершина просмотрена, то для нее D[i] есть наикратчайшее расстояние от вершины нач до вершины i.
предок[i]- информация о номере вершины, предшествующей вершине i в кратчайшем пути от вершины нач.
минрас — это минимальное расстояние.
Задан набор неповторяющихся пар (A i ,A j ), A i , A j принадлежат множеству А=. Необходимо составить цепочку максимальной длины по правилу
(A i ,A j )+(A j ,Ak)=(A i ,A j ,A k ).
При образовании этой цепочки любая пара может быть использована не более одного раза.
Между N пунктами (N
1) при заданных N,M и сети дорог единичной длины (все имеющиеся A(i,j)=1) определяет минимальное время, через которое может произойти встреча всех M роботов, при этом начальное положение роботов и скорость их движения известны.
2) Выполнить те же действия, что и в п. 1, но только для различных значений A(i,j).
Примечание: В случае невозможности встречи всех M роботов в одном месте ни в какой момент времени в результате выполнения программы должно быть сформировано соответствующее сообщение.
Требование к вводу-выводу:
1) Все входные данные — целые неотрицательные числа;
2) при задании сети дорог должно быть указано количество дорог — K и пункты их начала и конца в виде пар (i,j).
На плоскости расположено N точек. Имеется робот, который двигается следующим образом. Стартуя с некоторой начальной точки и имея некоторое начальное направление, робот движется до первой встреченной на его пути точки, изменяя в ней свое текущее направление на 90 градусов, т.е. поворачивая налево или направо. После этого он продолжает движение аналогично. Если робот достиг начальной точки, либо не может достичь новой точки (которую он еще не посещал), то он останавливается.
Определить, может ли робот посетить все N точек, если:
- Определены начальные точка и направление робота.
- Определена начальная точка, а направление робота можно выбирать.
- Начальную точку и направление робота можно выбирать.
Координаты точек — целые числа, угол измеряется в радианах относительно оси ОХ.
Найти кратчайшее расстояние между двумя вершинами в графе. Найти все возможные пути между этими двумя вершинами в графе не пеpесекающиеся по
Лабиринт задается матрицей смежности N*N, где C(i,j)=1, если узел i связан узлом j посредством дороги. Часть узлов назначается входами, часть — выходами. Входы и выходы задаются последовательностями узлов X(1). X(p) и Y(1). Y(k) соответственно.
Найти максимальное число людей, которых можно провести от
входов до выходов таким образом, чтобы:
а) их пути не пересекались по дорогам, но могут пеpесекаться по узлам;
б) их пути не пересекались по узлам;
N шестеpенок пpонумеpованы от 1 до N (N
На фигуре 1.показана вычислительная система, содержащая достаточное количество процессоров, использующих общую память из 26 числовых переменных A,B,C. Z. Система работает шагами. На каждом шаге, каждый процессор выполняет либо оператор присваивания либо пустой оператор. Оператор присваивания — это конструкция вида
где арифметическое выражение без скобок и содержит не более 2 переменных и арифметические операции. Процессоры вычисляют выражения и присваивают их значения переменным из левых частей операторов, а потом приступают к следующим операторам (при том одновременно). Не допускается одновременное выполнение 2 или больше операторов присваивания с одинаковой левой частью. Пустой оператор обозначаем символом &. Выполняя его, процессор простаивает 1 шаг.
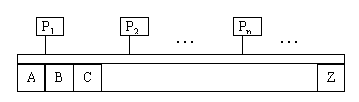
n последовательности операторов (присваивания или пустых) с одинаковой длиной L называем n-программой с длиной L (выполняется за L шагов на первых n процессоров), если на каждом шаге имеем не более 1 оператора с заданной левой частью. n-программы P и Q называем эквивалентными, если начиная с одного и того же начального состояния переменных A,B. Z после выполнения как P, так и Q получается одинаковый результат.
Напишите программу, которая:
Задание 1. Вводит целое k(k
Имеется N прямоугольных конвертов и N прямоугольных открыток различных размеров. Можно ли разложить все открытки по конвертам, чтобы в каждом конверте было по одной открытке.
Замечание. Открытки нельзя складывать, сгибать и т.п., но можно помещать в конверт под углом. Например, открытка с размерами сторон 5:1 помещается в конверты с размерами 5:1, 6:3, 4.3:4.3, но не входит в конверты с размерами 4:1, 10:0.5, 4.2:4.2.
Составить программу для нахождения произвольного разбиения 20 студентов на 2 команды, численность которых отличается не более чем в 2 раза, если известно, что в любой команде должны быть студенты, обязательно знакомые друг с другом. Круг знакомств задается матрицей (20,20) с элементами
Имеется N человек и прямоугольная таблица А[1:N,1:N];элемент A[i,j] равен 1, если человек i знаком с человеком j, А[i,j] = =А[j,i]. Можно ли разбить людей на 2 группы, чтобы в каждой группе были только незнакомые люди.
На олимпиаду прибыло N человек. Некоторые из них знакомы между собой. Можно ли опосредованно перезнакомить их всех между собой? (Незнакомые люди могут познакомиться только через общего знакомого).
Пусть группа состоит из N человек. В ней каждый имеет (N/2) друзей и не больше K врагов. У одного из них есть книга, которую все хотели бы прочитать и потом обсудить с некоторыми из остальных.
Написать программу, которая:
1. Находит способ передачи книги таким образом, чтобы она побывала у каждого в точности один раз, переходя только от друга к другу и наконец возвратилась к своему владельцу.
2.Разбивает людей на S групп, где будет обсуждаться книга, таким образом, чтобы вместе с каждым человеком в ту же самую группу вошло не более P его врагов.
Примечание: предполагается, что S*P>=K.
В заданном графе необходимо определить, существует ли цикл, проходящий по каждому ребру графа ровно один раз.
Следующая фигура показывает запутанную сеть дорог района города. Представьте, что мусорная машина должна пройти по всем дорогам хотя бы один раз, чтобы собрать мусор. Число на каждой стороне показывает время, которое должна потратить мусорная машина, чтобы проехать этот интервал. На перекрестках машина должна ждать время, равное числу пересекающихся дорог.
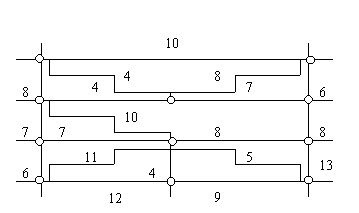
Составьте программу, показывающую как выбрать необходимый путь для сбора мусора в кратчайшее время.
Есть 11 остановок.
от 1 до 2 путь 10 мин.
N pазличных станков один за дpугим объединены в конвейеp. Имеется N pабочих. Задана матpица C[N , N], где C[i,j] пpоизводительность i-ого pабочего на j-ом станке. Опpеделить
а) на каком станке должен pаботать каждый из pабочих, чтобы пpоизводительность была максимальной.
б) то же, но станки pасположены паpаллельно и выполняют одноpодные опеpации.
На плоскости задан граф с N вершинами. Количество ребер, соединенных с каждой вершиной, равно 3.
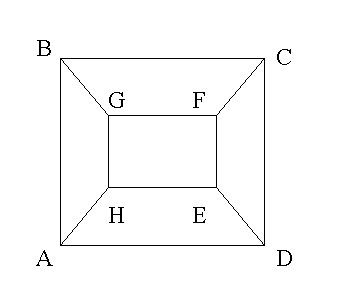
Пусть вершины X,Y и Z являются соседями вершины Т. Будем считать, что Y левый, а Z -правый сосед вершины Т относительно вершины X, если ориентированный угол XTZ меньше ориентированного угла XTY (положительным будем считать направление против часовой стрелки). Например вершина Е является правым соседом вершины Н относительно А, а G — левым, поскольку ориентированный угол АНЕ меньше ориентированного угла AHG. (Ребра считаются отрезками).
Составьте программу, которая:
1. Вводит координаты вершин графа и его ребра и рисует граф на экране компьютера, производя при этом подходящее масштабирование(Ребра выводятся как отрезки).
2. Пусть заданы две начальные соседние вершины X 0 и X 1 и последовательность вида LLRRL. Тогда программа находит путь на графе X 0 X 1 X 2 . X n для вершин которого выполнено:
-первые два являются заданными X 0 и X 1
-X i+1 является левым или правым соседом X i относительно X i-1 в зависимости от заданной последовательности, при том L означает левый, а R -правый.
Пример:В заданном графе пусть даны начальные вершины А и H и последовательность LRRLLR. Тогда программа должна найти путь AHGFEDCB.
3. Рисует на экране путь, найденный в п.2.
4. Пусть даны начальная и конечная вершина. Программа должна найти путь, проходящий через минимальное число вершин, вывести его на экран и найти 2 первые вершины и управляющую последовательность для этого пути, как определено в п.2.
Имеется N городов. Для каждой пары городов (I,J) можно построить дорогу, соединяющую эти два города и не заходящие в другие города. Стоимость такой дороги A(I,J). Вне городов дороги не пересекаются.
Написать алгоритм для нахождения самой дешевой системы дорог, позволяющей попасть из любого города в любой другой. Результаты задавать таблицей B[1:N,1:N], где B[I,J]=1 тогда и только тогда, когда дорогу, соединяющую города I и J, следует строить.
В картинной галерее каждый сторож работает в течение некоторого непрерывного отрезка времени. Расписанием стражи называется множество пар [Т 1 (i), Т 2 (i)] — моментов начала и конца дежурства i-го сторожа из интервала [0,EndTime].
Для заданного расписания стражи требуется:
(а) проверить, в любой ли момент в галерее находится не менее двух сторожей.
Если условие (а) не выполнено, то:
(б) перечислить все интервалы времени с недостаточной охраной (менее 2 сторожей).
(в) добавить наименьшее число сторожей с заданной, одинаковой для всех длительностью дежурства, чтобы получить правильное расписание (т.е. удовлетворяющее условию (а)).
(г) проверить, можно ли обойтись без добавления новых сторожей, если разрешается сдвигать времена дежурства каждого из сторожей с сохранением длительности дежурства.
(д) Если это возможно, то составить расписание с наименьшим числом сдвигов.
(Все моменты времени задаются в целых минутах.)
EndTime — момент окончания стражи, т.е. охраняется отрезок времени [0, EndTime].
N -число сторожей.
T 1 [i], T 2 [i], i=1. N — моменты начала и окончания дежурства i-го сторожа.
Length — длительность дежурства каждого дополнительного сторожа.
(1) Ответ на пункт (а) в форме да/нет.
(2) При ответе «нет» на п. (а) — список пар (k,l) — начал и концов всех малоохраняемых интервалов с указанием числа сторожей в каждом (0 или 1).
(3) Число дополнительных сторожей и моменты начала и окончания дежурства каждого дополнительного сторожа.
(4) Ответ на пункт (г) в форме да/нет. Если «да», то номера сторожей, смена которых сдвигается, и значения сдвигов.
(5) В ответ на пункт (д): наименьшее число сторожей, смена которых сдвигается, их номера и значения сдвигов.
Программа должна допускать независимое тестирование пунктов (в), (г), (д).
Вводится N — количество домов и К — количество дорог. Дома пронумерованы от 1 до N. Каждая дорога определяется тройкой чисел — двумя номерами домов — концов дороги и длиной дороги. В каждом доме
живет по одному человеку. Найти точку — место встречи всех людей, от которой суммарное расстояние до всех домов будет минимальным.
Если точка лежит на доpоге, то указать номера домов — концов этой доpоги и расстояние от первого из этих домов. Если точка совпадает с домом, то указать номер этого дома.
Примечание: длины дорог — положительные целые числа.
N колец сцеплены между собой (задана матрица A(n*n), A(i,j)=1 в случае, если кольца i и j сцеплены друг с другом и A(i,j)=0 иначе). Удалить минимальное количество колец так, чтобы получилась цепочка.
Янка положил на стол N выпуклых K-гранников и N различных типов наклеек по K штук каждая. Ночью кто-то наклеил наклейки на грани, по одной на грань.
Помогите Янке расставить многогранники так, чтобы наклейка каждого типа была видна pовно K-1 раз.
Имеется N точек и M проводков. Проводком можно соединить некоторую пару различных точек, причем пара может быть соединена не более чем одним проводком. Все проводки должны быть использованы.
Пусть D i — количество проводков, которые будут соединены с точкой с номером i, i=1, . N.
Необходимо соединить N точек с помощью M проводков таким образом, чтобы сумма S=D 1 *D 1 + D 2 *D 2 + . + D n *D n была максимальной.
Вывести величины D i в неубывающем порядке и. по требованию
(priznak=1), список соединений.
ВВОД:
N (N M (M D i в неубывающем порядке.
S
список точек
.
список точек
Задано N городов c номерами от 1 до N и сеть из M дорог с односторонним движением между ними. Каждая дорога задается тройкой (i, j, k), где i — номер города, в котором дорога начинается, j —
номер города, в котором дорога заканчивается, а k — ее длина (число k — натуральное). Дороги друг с другом могут пересекаться только в концевых городах.
Все пути между двумя указанными городами A и B можно упорядочить в список по неубыванию их длин (если есть несколько путей одинаковой длины, то выбираем один из них). Необходимо найти один из путей, который может быть вторым в списке.
Вывести его длину L и города, через которые он проходит.
ВВОД:
N M
i 1 , j 1 , k 1
.
i M , j M , k M
A, B
ВЫВОД:
или
A, i 1 , i 2 , . B
L
Рассмотрим пример нахождение кратчайшего пути. Дана сеть автомобильных дорог, соединяющих области города. Некоторые дороги односторонние. Найти кратчайшие пути от центра города до каждого города области.
Для решения указанной задачи можно использовать алгоритм Дейкстры — алгоритм на графах, изобретённый нидерландским ученым Э. Дейкстрой в 1959 году. Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Работает только для графов без рёбер отрицательного веса.
Пусть требуется найти кратчайшие расстояния от 1-й вершины до всех остальных.
Кружками обозначены вершины, линиями – пути между ними (ребра графа). В кружках обозначены номера вершин, над ребрами обозначен их вес – длина пути. Рядом с каждой вершиной красным обозначена метка – длина кратчайшего пути в эту вершину из вершины 1. 
Инициализация
Метка самой вершины 1 полагается равной 0, метки остальных вершин – недостижимо большое число (в идеале — бесконечность). Это отражает то, что расстояния от вершины 1 до других вершин пока неизвестны. Все вершины графа помечаются как непосещенные. 
Первый шаг
Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6. Обходим соседей вершины по очереди.
Первый сосед вершины 1 – вершина 2, потому что длина пути до неё минимальна. Длина пути в неё через вершину 1 равна сумме кратчайшего расстояния до вершины 1 (значению её метки) и длины ребра, идущего из 1-й во 2-ю, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2 (10000), поэтому новая метка 2-й вершины равна 7. 
Аналогично находим длины пути для всех других соседей (вершины 3 и 6).
Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит. Вершина 1 отмечается как посещенная.
Второй шаг
Шаг 1 алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это вершина 2 с меткой 7.
Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю вершину. Соседями вершины 2 являются вершины 1, 3 и 4.
Вершина 1 уже посещена. Следующий сосед вершины 2 — вершина 3, так как имеет минимальную метку из вершин, отмеченных как не посещённые. Если идти в неё через 2, то длина такого пути будет равна 17 (7 + 10 = 17). Но текущая метка третьей вершины равна 9, а 9 Реализация на C++
#define _CRT_SECURE_NO_WARNINGS
#include
#include
#define SIZE 6
int main()
<
int a[SIZE][SIZE]; // матрица связей
int d[SIZE]; // минимальное расстояние
int v[SIZE]; // посещенные вершины
int temp, minindex, min;
int begin_index = 0;
system( «chcp 1251» );
system( «cls» );
// Инициализация матрицы связей
for ( int i = 0; i for ( int j = i + 1; j «Введите расстояние %d — %d: » , i + 1, j + 1);
scanf( «%d» , &temp);
a[i][j] = temp;
a[j][i] = temp;
>
>
// Вывод матрицы связей
for ( int i = 0; i for ( int j = 0; j «%5d » , a[i][j]);
printf( «n» );
>
//Инициализация вершин и расстояний
for ( int i = 0; i // Шаг алгоритма
do <
minindex = 10000;
min = 10000;
for ( int i = 0; i // Если вершину ещё не обошли и вес меньше min
if ((v[i] == 1) && (d[i] // Переприсваиваем значения
min = d[i];
minindex = i;
>
>
// Добавляем найденный минимальный вес
// к текущему весу вершины
// и сравниваем с текущим минимальным весом вершины
if (minindex != 10000)
<
for ( int i = 0; i if (a[minindex][i] > 0)
<
temp = min + a[minindex][i];
if (temp while (minindex // Вывод кратчайших расстояний до вершин
printf( «nКратчайшие расстояния до вершин: n» );
for ( int i = 0; i «%5d » , d[i]);
// Восстановление пути
int ver[SIZE]; // массив посещенных вершин
int end = 4; // индекс конечной вершины = 5 — 1
ver[0] = end + 1; // начальный элемент — конечная вершина
int k = 1; // индекс предыдущей вершины
int weight = d[end]; // вес конечной вершины
while (end != begin_index) // пока не дошли до начальной вершины
<
for ( int i = 0; i // просматриваем все вершины
if (a[i][end] != 0) // если связь есть
<
int temp = weight — a[i][end]; // определяем вес пути из предыдущей вершины
if (temp == d[i]) // если вес совпал с рассчитанным
< // значит из этой вершины и был переход
weight = temp; // сохраняем новый вес
end = i; // сохраняем предыдущую вершину
ver[k] = i + 1; // и записываем ее в массив
k++;
>
>
>
// Вывод пути (начальная вершина оказалась в конце массива из k элементов)
printf( «nВывод кратчайшего путиn» );
for ( int i = k — 1; i >= 0; i—)
printf( «%3d » , ver[i]);
getchar(); getchar();
return 0;
>
Коммуникационная сеть минимальной длины
Построение коммуникационной сети минимальной длины
Коммуникационная сеть минимальной длины (или дерево кратчайших расстояний) – это совокупность дуг сети, имеющая минимальную суммарную длину и обеспечивающая достижение всех узлов сети, т.е. возможность попасть из любого узла в любой другой узел.
Начать с любого узла и соединить его с ближайшим узлом. Считаем, что эти узлы связанные, а все другие несвязанные.
Определить несвязанный узел, ближайший к одному из связанных узлов. Если таких «ближайших» узлов несколько, то выбрать любой. Добавить этот узел к связанным. И т.д., до тех пор, пока есть несвязанные узлы.
Пример. Университет устанавливает компьютерную систему электронной почты, которая позволит передавать сообщения между деканами восьми факультетов. Сеть возможных электронных связей между деканатами показана ниже. Протяженность коммуникаций в километрах отмечена на дугах.
Необходимо предложить проект системы связи, которая позволит всем восьми деканам обеспечить доступ к системе электронной почты. Решение должно обеспечить минимальную возможную общую длину коммуникаций.

Длина коммуникаций равна сумме расстояний на дугах:
Задача определения кратчайшего пути Метод присвоения меток
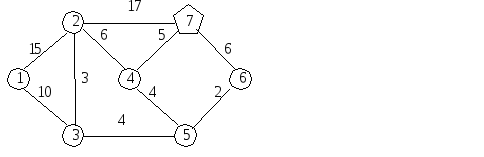
Задача состоит в том, чтобы найти кратчайший путь на графе от какой-то выделенной вершины до любой другой вершины.
Пример: Узел 7 – склад, остальные узлы – строительные площадки компании. Показатели на дугах – расстояния в километрах.

Надо найти кратчайшие расстояния от склада до каждой строительной площадки.
Каждому узлу приписывают метку из двух чисел:
первое число – минимальное расстояние от узла 7 до данного узла,
второе – номер предыдущего узла на пути от узла 7 к данному узлу.
Помеченным называют узел, для которого определен путь от узла 7. Иначе узел – непомеченный.
Если кратчайшее расстояние от узла 7 до данного узла определено, то соответствующая метка постоянная и обозначается в круглых скобках. Остальные метки временные и обозначаются в квадратных скобках. Узлы с постоянными метками закрашиваем.
Узлу 7 присваиваем метку (0, S), где 0 – расстояние от узла 7, S – обозначение стартового узла.
Узел 7 связан с узлами …. Им присваиваем соответствующие метки –

После выполнения этой операции выполняют два шага:
находят участок минимальной длины и соответствующую временную метку делают постоянной;
узел, которому соответствует данная постоянная метка становится новым стартом.
Метка с наименьшим расстоянием соответствует узлу …. Этот узел объявляем помеченным и заменяем скобки у метки.

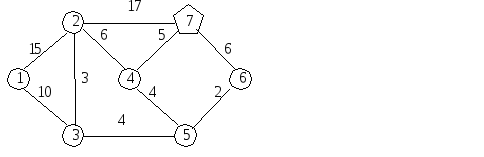
Узел … связан непосредственно с узлами без постоянных меток. Временная метка узла … равна [ ]=[ ], а у узла … – [ ]= [ ]. Т.к. узел … уже имеет временную метку [ ], то из двух меток выбираем ту, в которой расстояние меньше, т.е. [ ].
Из всех временных меток [ ], [ ], [ ] выбираем метку с наименьшим первым числом – [ ]. Она становится постоянной и очередной шаг начинаем с узла ….

Этот узел связан только с узлом … без постоянной метки. Временная метка узла … равна [ ]=[ ]. Эта метка имеет меньшее первое число, чем предыдущая, поэтому узлу … приписываем новую временную метку [ ].
Из всех временных меток [ ], [ ] метку с наименьшим первым числом [ ] объявляем постоянной и следующий шаг начинаем с соответствующего ей узла ….

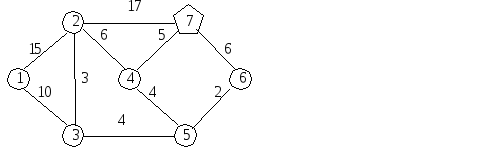
Узел … связан только с одним узлом без постоянной метки – узлом …. Временная метка узла … равна [ ]=[ ].
Из всех временных меток [ ], [ ] метку с наименьшим первым числом [ ] объявляем постоянной и следующий шаг начинаем с соответствующего ей узла .

Узел … связан с узлами без постоянных меток. Временная метка узла … равна [ ]=[ ], а узла … – [ ]=[ ]. Т.к. узел … уже помечен меткой с меньшим первым числом, то метку не меняем.
Из временных меток [ ], [ ] метка с наименьшим первым числом [ ] становится постоянной и следующий шаг начинаем с соответствующего ей узла ….
Метку узла … меняем на ( )=( ).

Всем узлам приписаны постоянные метки. Действие алгоритма прекращается.
Первое число метки у каждой вершины – это длина кратчайшего пути от узла 7 до данной вершины. Чтобы восстановить кратчайший путь от узла 7 до какой-то вершины, нужно из этой вершины перейти в соседнюю (ее номер – второе число метки) и т.д. до вершины 7.
Определим кратчайшие расстояния от склада до каждой строительной площадки:
Построение коммуникационной сети минимальной длины
Коммуникационная сеть минимальной длины (или дерево кратчайших расстояний) – это совокупность дуг сети, имеющая минимальную суммарную длину и обеспечивающая достижение всех узлов сети, то есть возможно попасть из любого узла в любой другой узел.
1) Начать с первого узла и соединить его с ближайшим. Соединенные узлы называются связанными, а не соединенные – не связанными.
2) Определить несвязанный узел, ближайший к одному из связанных. Если таких узлов несколько, то выбрать любой. Добавить этот узел к связанным. И так до тех пор, пока есть несвязанные узлы.
Пример. Организация планирует создать локальную сеть, объединяющую территориально распределенные структурные подразделений, расстояния между которыми, в км, отражены на схеме.
Найти коммуникационную сеть минимальной длины.
Начнем с узла 1, ближайший к нему – узел 2, поэтому соединим их жирной линией.
Далее ближайший узел к двум имеющимся связанным узлам (1,2) – третий и шестой. Выбираем любой из них, например шестой, и соединяем со вторым.
Продолжаем пока не останется ни одной не соединенной ячейки. В итоге должно получиться так
Итоговая длина коммуникационной сети равна сумме длин выделенных дуг связывающих узлы: 2+3+1+1+0,5+1+2=10,5 км.
Понятие логистических издержек и их экономическое содержание.
Издержки – израсходованная на что-нибудь сумма, затраты.
Затраты – то, что истрачено, израсходовано. Расход – затраты, издержки, потребленные затраты чего-нибудь для определенной цели. FC-постоянные издержки, которые независимо от условий должны быть. VC-переменные издержки. TC –валовые (общие, явные) издержки. TC = FC + VC. AC – средние издержки = TC/Q. Q-количество произведенной продукции. MC – предельные издержки = дельтаTC/дельта Q.
Логистические издержки – денежное выражение, использованной рабочей силы средств и предметов труда, финансовые затраты и различные негативные последствия форс-мажорные обстоятельства, которые обусловлены продвижением материальных ценностей на предприятии и между ними, а также поддержание запасов.
Логистич. идержки формируются в результате функционирования каналов снабжения, распределения и производственных процессов. В общем виде лог.издержки отдельного предприятия м.б. представлены как сумма 3х основных составляющих:
— издержки транспортно-снабженческих сетей;
— издержки производственно-технологических, операционных сетей;
— издержки сбытовых, транспортно-распределительных цепей.
113Классификация логистических затрат по разл. Критериям. Учет логистических издержек.
А) по отношению к ГП:
— ЛЗ, относящиеся к готовому продукту;
— ЛЗ, относящиеся к периоду времени.
Б) по видам затрат:
— материальные затраты (амортизация, потребленные материалы, топливо, энергия, сторонние мат.услуги;
— нематериальные затраты ( на оплату труда, немат.услуги, стоимость привлечения стороннего капитала, налоги, платежи, и прочие форс-мажорные издержки, отражающиеся на фин.показателях предприятия.
В) по отношению к объему производства:
Г) по способу включения в себестоимость:
— прямые (сырье, осн. М-лы, покупные изделия и полуфабрикаты, осн.з.п. производств. Рабочих);
— косвенные (ремонт и содержание универсального оборудования, время общепроизводственные расходы, часть непроизв. Издержек)
Д) по роли в технолог. процессе изготовления продукции и целевому назначению:
— основные (затраты, входящие в состав цеховой себестоимости);
— накладные (коммерческие расходы, общехоз. Р-ды).
Е) по обеспечению системы контроля: — контролируемые; — неконтролируемые
Ж) по степени регулируемости: — полностью регулируемы; — частично; — заданные затраты.
З) по местам возникновения: — затраты функциональных подразделений (отдел снабжения, реализация,тр-т); — затраты подразделений, связанных с движением потока (склад, пр-во).
И) в зависимости от сферы и функций деятельности предприятий: -снабженческо-заготовительные; — коммерческо-сбытовые; — организационно-управленческие; — технологические.
К) по процессам: — на пр-во; — на реализацию пр-ва; — на управление предприятием
Л)по целевому назначению: — на содержание тов.запасов; — реализацию т-ров; — на отсутствие тов.зап-в
М) по осн. Фазам движения: — закупки; — пр-во; — реализация
Н) по осн. Компонентам лог. Процессов: — з-ты на физ.продвижение материалов; — на протекание информ. Процессов; — на запасы.
Затраты на физическое продвижение материалов включают амортизационные отчисления по осн. Средствам, используемых в лог. Процессах; затраты на использованные материалы, топливо и энергию; прочие расходы на продвижение (сумма налогов на недвижимость, налог на тр. Ср-ва, налог на землю). Эти затраты представляют внутренние расходы предприятия.
Затраты, связанные, с запасом включают затраты на формирование запасов на поддержание запасов и издержки в результате исчерпания запасов.
Группировка лог. З-т по осн. Фазам продвижения, строятся на выделении фаз процессов закупки, пр-ва, реализации.
114 Цепочка ценностей – система взаимосвязанных видов деятельности, создающих стоимость.
Для ЛС цепочка ценностей отражает взаимосвязи фокусной компании в цепи поставок с поставщиками и каналами распределения, оптимизируя кот. Она может получить преимущества в конкурентной борьбе. Концепция цепочки ценностей заключается в структурировании действий по всему циклу движения продукции, от исходного сырья до конечной потребления по стратегически важным видам эконом. Деятельности. Обычно реализуется только часть этапов в системе формирования ценностей (в рамках предприятия). ЦЦ для каждого предприятия уникальна. Организации, связанные с одной и той же ЦЦ постоянно взаимодействуют друг с другом. Если одна несет убытки или является банкротом, то это отражается на всех организациях цепочки и поэтому нерац. Использование ресурсов и замораживание оборотных средств явл. проблемами для каждого звена и всей ЛС в целом.
Для минимизации общих затрат по ЦЦ требуется провести неск-ко видов работ:
— определение полезности бизнес-процессов и звеньев ЛС;
— проанализировать доходы и затраты по элементам ЦЦ;
— определить эконом. Статус элементов по результатам проведенного анализа.
В составе ЦЦ с позиции внутреннего или внешнего потребителя иногда обнаруживаются лишние операции в т.ч лог., которые добавляют стоимость, но не ценность для конечного потребителя. Задача- устранение, выявление операций.
Возможности оценки элементов ЦЦ рассмотрим на примере сост. Полного складского процесса хранения и грузопереработки до момента отгрузки его потребит.

При анализе элементов ЦЦ исследуются ключевые показатели функционирования (KPI):
— производительность; — качество; — издержки и влияющие на них факторы.
115 Понятие и виды лог. Контроллинга. Система «стандарт-кост». Калькулирование полной себестоимости продукции.
Развитие теории и практики управления издержками и необходимость обеспечения прибыльной деятельности предприятий привели к формированию контроллинга в 1970-х годах как целостной концепции экономического управления предприятием, ориентирующей руководителей на выявление всех возможностей и рисков, связанных с получением прибыли. Контроллинг основан на принципах директ-коста (расчет себест-ти путем деления издержек на постоянные и переменные). Но как система управления затратами может включать и стандарт-кост, и другие аналогичные методы.
Контроллинг шире стандарт-коста и директ-коста, разнообразнее по назначению, функциям, методам планирования, учета и анализа, степени использования информации. Он не ограничивается контролем издержек (функция стандарт-коста) и не только контролирует рентабельность выпуска и реализации продукции (основная функция директ-коста), но и обеспечивает достижение поставленной предприятием цели, как правило, получение максимальной прибыли. Контроллинг часто выполняет функции внутреннего контроля на предприятии, контроля эффективности работы его подразделений и организации в целом. В отличии от ревизии он ориентируется на текущие результаты деятельности и не связан с документальной проверкой, необходимостью выхода на места совершения хозяйственных актов и операций. Система контроллинга особенно целесообразна в тех случаях, когда функции управления предприятием делегированы его отделам и службам. Тогда он помогает им в достижении максимально возможного общего результата деятельности. В составе функций контроллинга можно выделить сервисную функцию предоставления необходимой информации для управления и комментирующую функцию для принятия решений и их координации.
Информационное обслуживание контроллинга обеспечивается с помощью системы планирования, нормирования, учета и конроля, ориентированной на достижение цели, конечного результата деятельности. Информация должна содержать заданные (нормативные, плановые) и фактические данные, отклонения, выявленные средствами учета в разрезе подразделений предприятий.
Комментирующая функция контроллинга состоит в использовании данных анализа отклонений, ставок покрытия, общих результатов деятельности для принятия управленческих решений.
Существуют два уровня контроллинга: стратегический и оперативный. Стратегическийнаправлен на создание потенциала успеха, т.е. обеспечение долгосрочного существования предприятия. Его задача – отслеживание адаптации предприятия к окружающей среде, т.е. выявление целесообразности продолжения намеченных стратегических мероприятий в течение срока реализации стратегического плана.
Оперативный контроллинг направлен на достижение запланированного уровня дохода (прибыли). Его главной задачей является оценка экономической эффективности производственных процессов, выявление «узких мест», вызывающих отклонение ожидаемой (фактической) прибыли от запланированной.
Контроллингу присущ специфический инструментарий, т.е. взаимосвязанная совокупность методов получения, обработки, агрегирования, анализа, предоставления и использования разнообразной экономической информации.
Главными задачами контроллинга являются:
* участие в выработке целей предприятия (системы);
* предложение альтернативных решений на основе имеющейся информации;
* анализ экономической эффективности (особенно инвестиций и инноваций);
* руководство при разработке оперативных плановых смет;
* сравнение плановых показателей с фактическими и разработка предложений по преодолению отклонений;
* определение «узких мест»;
* создание систем информации для планирования и управления;
* консультации руководителей предприятия по производственно-экономическим вопросам;
* производственно-экономическое обоснование информации других специализированных отделов.
«Стандарт-кост» — расчет затрат производится на базе нормативов, а управление осуществляется по отклонению затрат от нормативных. Выявление, учет, анализу лог. З-т д.б. систематизир. и скоординиров. Этим должен заниматься отдел логистики, которые анализирует структуру, ищет пути оптимизации и снижению затрат с целью учета и регулир.
Задача о построении коммуникационной сети минимальной длины
Всем привет! Ребят очень нужна помощь! Слаб в программирование. Необходимо реализовать в любом языке но желательно VB или в ms Exel vba. Плиз ДОБРЫЕ ЛЮДИ
Задача о построении коммуникационной сети минимальной длины
Коммуникационная сеть минимальной длины (дерево кратчайших расстояний) – это совокупность дуг сети, имеющая минимальную суммарную длину и обеспечивающая достижение всех узлов сети. Такие задачи возникают в фирмах, занимающихся прокладками коммуникационных сетей для компьютерных систем, систем кабельного телевидения, энергетических и телефонных сетей и т.д. Необходимо спроектировать базу данных, хранящую информацию обо всех необходимых для решения задачи данных, таких как:
• расстояние между пунктами размещения узлов сети;
• возможность прокладки между ними коммуникаций;
• стоимость прокладки связи на единицу расстояния;
• другие.
Для реализации бизнес процесса необходимо запрограммировать один из известных методов поиска дерева кратчайших расстояний. Вывести полученную сеть в удобной для анализа пользователя форме.
СОбственно Конкретные данные исходные можно додумать.. Нужна простенькая программа
17.01.2013, 18:30
Строки. Поиск слова минимальной длины, вывод этой длины, номер слова и само слово
Как организовать решение такой задачи? Может как-то через создание массивов, в ячейках которых.
В файле заменить все слова максимальной длины на слова минимальной длины
Нужно в считанном из файла тексте заменить все слова максимальной длины на слова минимальной длины.
 Поменять первое слово максимальной длины и последнее слово минимальной длины
Поменять первое слово максимальной длины и последнее слово минимальной длины
Отсортировать по убыванию слова любого предложения. Поменять первое слово максимальной длины и.
17.01.2013, 18:30
Заказываю контрольные, курсовые, дипломные и любые другие студенческие работы здесь.
Слово максимальной длины заменить на слово минимальной длины
Задача: Создать 2 объекта разработанного класса. Одной из компонент класса является символьная.
 Найти слово минимальной длины
Найти слово минимальной длины
Помогите пожалуйста решить. Дан текст, в котором слова отделяются пробелами, в конце стоит точка.
 Нахождение слова минимальной длины
Нахождение слова минимальной длины
Доброе время суток Имеется такой код просто вывода текста из файла на экран(Слов в файле несколько.
 Указание минимальной длины строки
Указание минимальной длины строки
Привет! Мне нужно указать минимальную длину строки во write Я указываю место сохранения файла в.
Алгоритмы о выборе дороги и сетях. Сети Штейнера. Лекция Владимира Протасова в Яндексе
Сегодня мы поговорим об одной из первых задач теории больших сетей, которая может быть решена полностью на самом простом базовом уровне, но которая от этого не становится менее интересной. Это задача о кратчайшей системе дорог или задача Штейнера.
Впервые она появилась, когда еще никаких практических надобностей для больших сетей не было: в тридцатые годы XX века. На самом деле Штейнер начал ее изучать еще раньше, в XIX веке. Это была чисто геометрическая задача, практические приложения которой стали известны только несколько десятилетий спустя.
Разговор пойдет о той области математики, которая впоследствии выросла в теорию больших сетей и разбилась на несколько областей. Это прикладная отрасль, которая задействует очень много методов из других математических дисциплин: дискретной математики, теории графов, функционального анализа, теории чисел и т.д. Бурное развитие теории больших сетей пришлось на конец девяностых и начало двухтысячных годов. Связано это конечно, с прикладными задачами: развитием интернета, мобильной связи, транспортных задач для больших городов. Кроме того теория сетей используется в биологии (нейронные сети), при построении больших электронных плат и т.п.
Сама задача формулируется очень просто. Есть несколько точек на плоскости, которые нужно связать системой дорог наименьшей суммарной длины таким образом, чтобы по этим дорогам можно было из каждой точки добраться в любую другую. Число точек конечно.
Начать рассказ стоит с истории о том, как на Малом мехмате двум группам учеников – восьмиклассникам и одиннадцатиклассникам дали решать одну и ту же задачу. Четыре деревни расположены в вершинах квадрата со стороной четыре километра. Существует ли система дорог, которая связывала бы все эти деревни между собой и имела бы суммарную длину не превосходящую 11 километров.
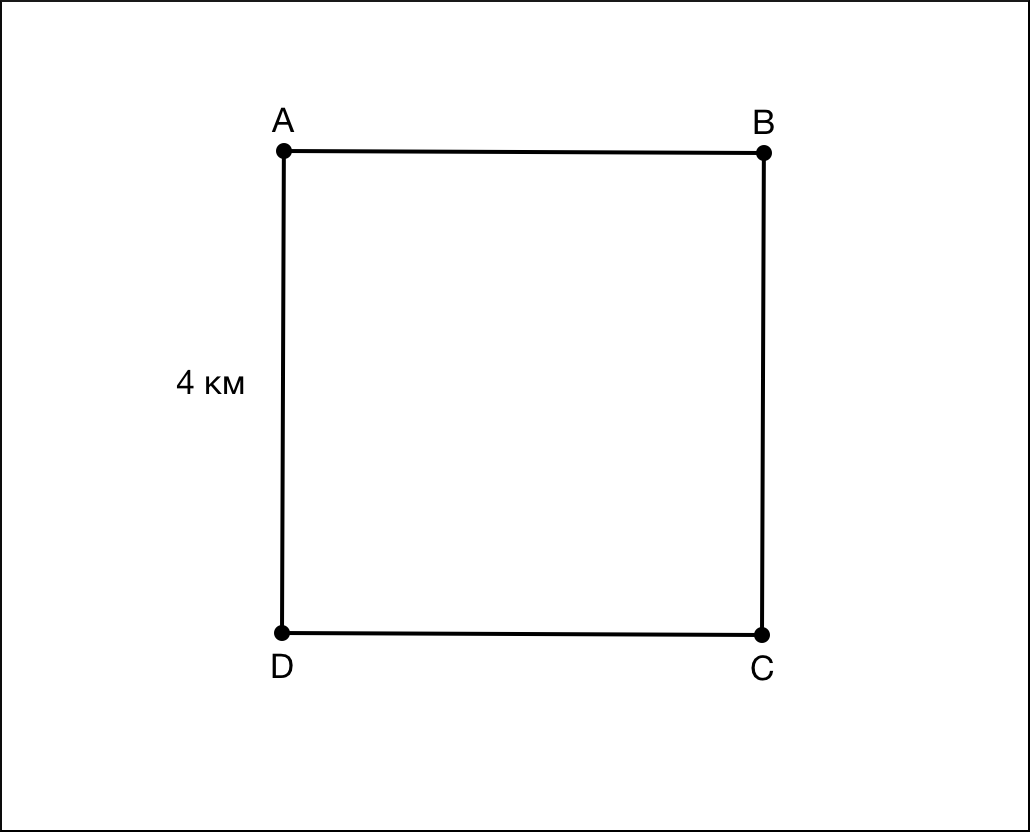
Если соединять деревни последовательно, то ничего короче, чем три стороны квадрата мы не придумаем. При таком соединении у нас будет ровно 12 километров. Можно соединять по диагонали, но это будет только хуже, т.к. диагональ длиннее стороны.

Если поставить дополнительную вершину, тогда из нее можно будет проехать в любые четыре деревни. Если мы возьмем дороги, связывающие диаметрально противоположные вершины, то по неравенству треугольника, сумма их длин будет больше, чем длина диагонали. У и двух других сумма длин тоже больше, чем длина диагонали. Соответственно, сумма всех дорог у нас будет ≥2∙4√2=8√2≈11.31. Примерно так рассуждали одиннадцатиклассники, которые пытались доказать невозможность существования такой системы дорог.
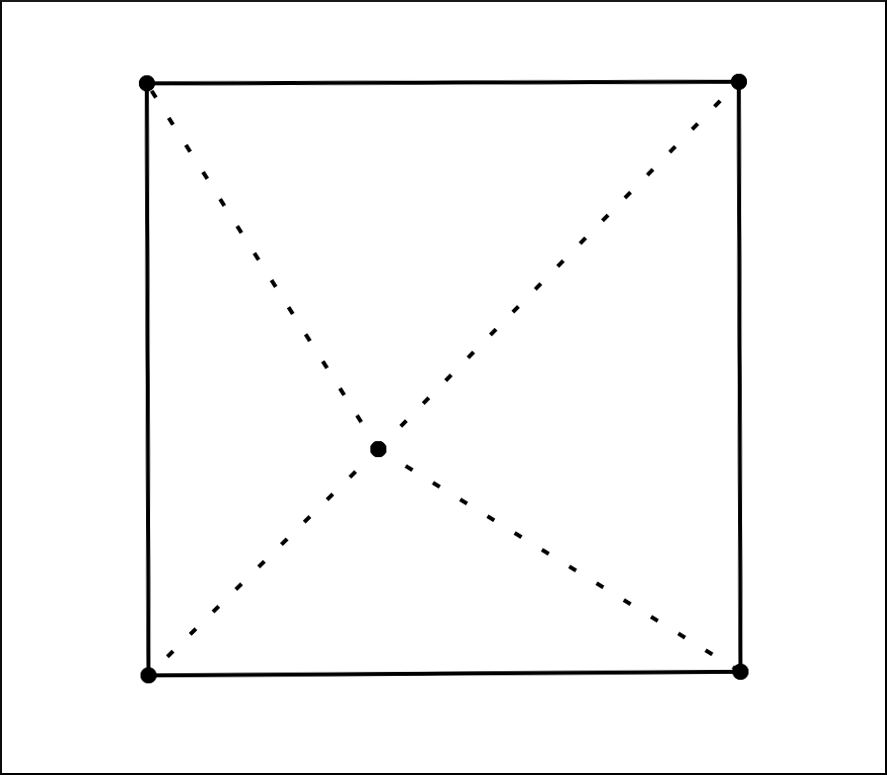
В это же самое время в соседней аудитории восьмиклассники при помощи обычной линейки с делениями строили эту самую систему дорог. И в итоге им это удалось. Система представляет собой нечто похожее на букву Н, все углы в которой равны 120°. Ее длина составляет ≈10.98 километра. Это и есть сеть Штейнера, соединяющая четыре точки. Таких сетей может быть много, может быть несколько кратчайших, но такую задачу о кратчайшей системе дорог можно решить полностью методами элементарной геометрии.

Чтобы окончательно покончить с этой задачей, найдем ошибку в первом решении, где мы вроде как доказали, что ничего короче 8√2 быть не может. Просто в этом решении не была учтена возможность многократно использовать один и тот же участок.
Три точки
Сеть Штейнера для треугольника была известна еще за 200 лет до самого Якоба Штейнера, в XVII веке. Это так называемая точка Ферма-Торичелли-Штейнера.
Начнем мы с того, что докажем одно вспомогательное утверждение, называемое иногда теоремой Помпею. Если мы возьмем на плоскости равносторонний треугольник и любую другую точку плоскости, тогда сумма расстояний до двух вершин A и B всегда больше или равно расстоянию до третьей вершины C: MA + MB ≥ MC. Более того, MA + MB = MC только в том случае, когда точка M лежит на дуге описанной окружности, не содержащей точку С. Т.е. угол AMB должен быть равен 120°. В противном случае MA + MB > MC.

Конечно, если речь идет о равностороннем треугольнике, нам часто в таких задачах помогает поворот на 60° относительно какой-нибудь вершины. Это мы и сделаем: повернем заштрихованный треугольник AMB относительно вершины A по часовой стрелке. Точка B у нас перейдет в точку C, а Точка M – в точку M’. В итоге у нас получается, что AM = AM’ = MM’, а M’C = MB.Теперь мы можем применить обычное неравенство треугольника на треугольнике MM’C. В нем сумма двух сторон M’M и M’C больше, чем MC. Соответственно, MA + MB ≥ MC. А когда же достигается равенство? Равенство достигается, когда точка M’ точно попадает на прямую MC, т.е. когда угол AMC равен 120°.
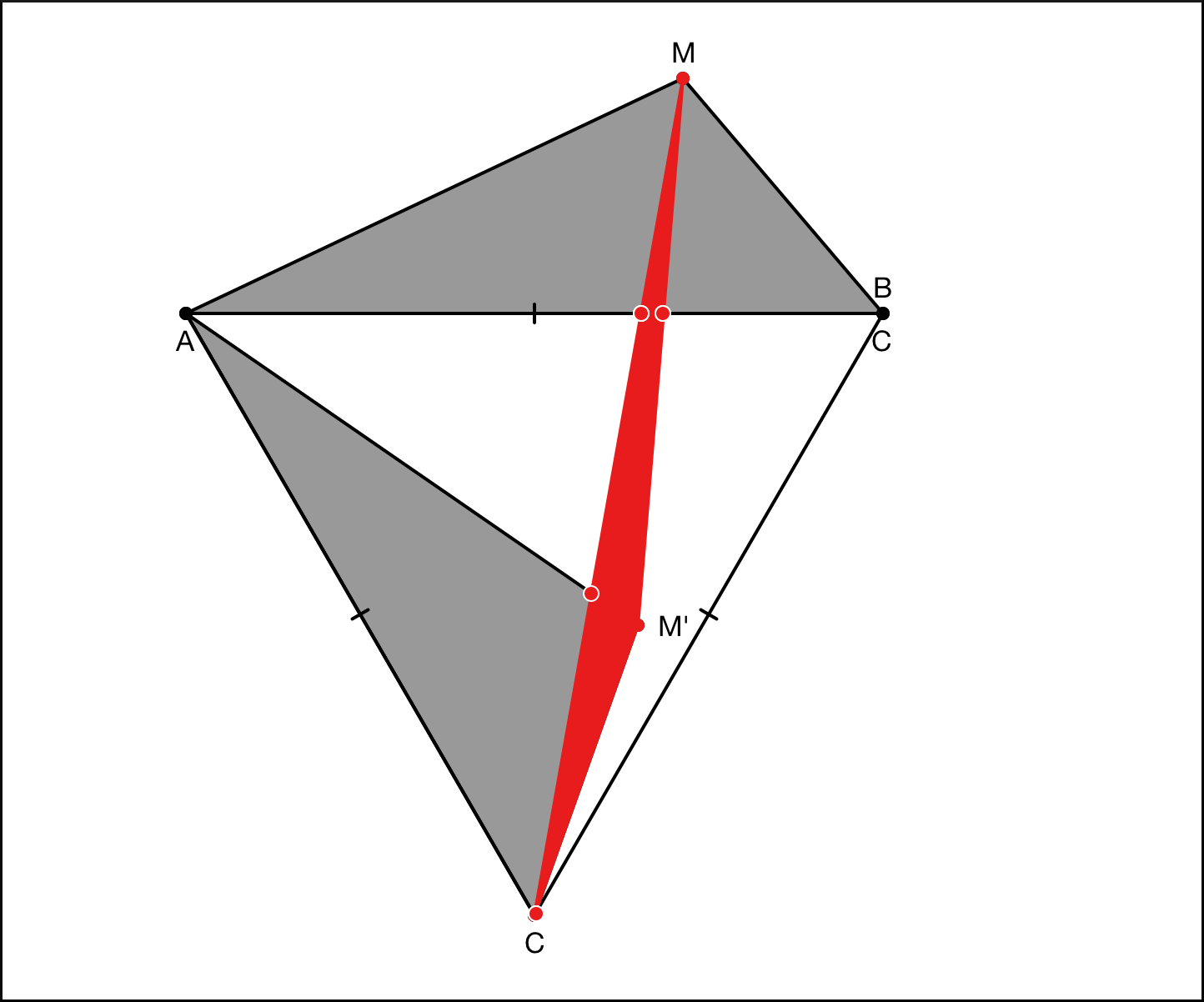
Теперь перейдем непосредственно к задаче Штейнера для трех точек. Формулируется она следующим образом. Задан треугольник. Нужно найти точку на плоскости, сумма расстояний от которой до вершин этого треугольника наименьшее. TA + TB + TC → min.

Что же это за точка? Мы знаем несколько замечательных точек треугольника: центры вписанной и описанной окружностей, точка пересечения медиан, точка пересечения высот. К сожалению, ни одна из них на роль точки с наименьшей суммой расстояний не подходит. Эта точка совершенно особая, и называется по-разному: точкой Торичелли, точкой Ферма, точкой Штейнера. Представляет она собой точку, из которой все три вершины треугольника видны под одинаковыми углами – 120°. Разберемся, почему это именно так. Впервые решение задачи о точке с наименьшей суммой расстояний до всех вершин треугольника документально впервые появилось в книге итальянского физика и математика Винченцо Вивиани в середине XVII века. Однако известно, что решение этой задачи было получено еще раньше другом Вивиани, Эванджелиста Торичелли – оба они были учениками Галилея. Приведенное в книге решение не было геометрическим, оно было основано на физических принципах. Эту задачу до Торичелли знал, а возможно, и решил Пьер Ферма: они состояли в переписке, и про эту задачу Торичелли узнал именно от Ферма, но было ли у нег свое решение – неизвестно.
Первое геометрическое решение этой задачи появилось лишь спустя 200 лет, и автором его стал Якоб Штейнер. Он был одним из первых синтетических геометров, решавшим геометрические задачи исключительно геометрическими методами. Основывалось решение Штейнера на рассмотренной нами выше теореме Помпею.
Существует ли вообще такая точка, из которой все углы треугольника видны под углом 120°? Существует она не всегда, а только в том случае, если все углы треугольника строго меньше 120°.
Если все углы треугольника > 120°, то существует единственная точка Торичелли. Построим равносторонний треугольник во внешнюю сторону относительно стороны BC. Построим окружность, которая проходила бы через точки B, A’ и C. Если тока Торичелли в данном случае существует, то она должна лежать на этой окружности, на дуге между точками B и C. Во вписанном четырехугольнике сумма противоположных углов составляет 180°. Треугольник BA’C равносторонний, соответственно, все углы в нем равны 60°. А значит, если мы поставим точку на дуге между точками B и C, а затем достроим четырехугольник, угол напротив вершины A’ будет равен 120°.
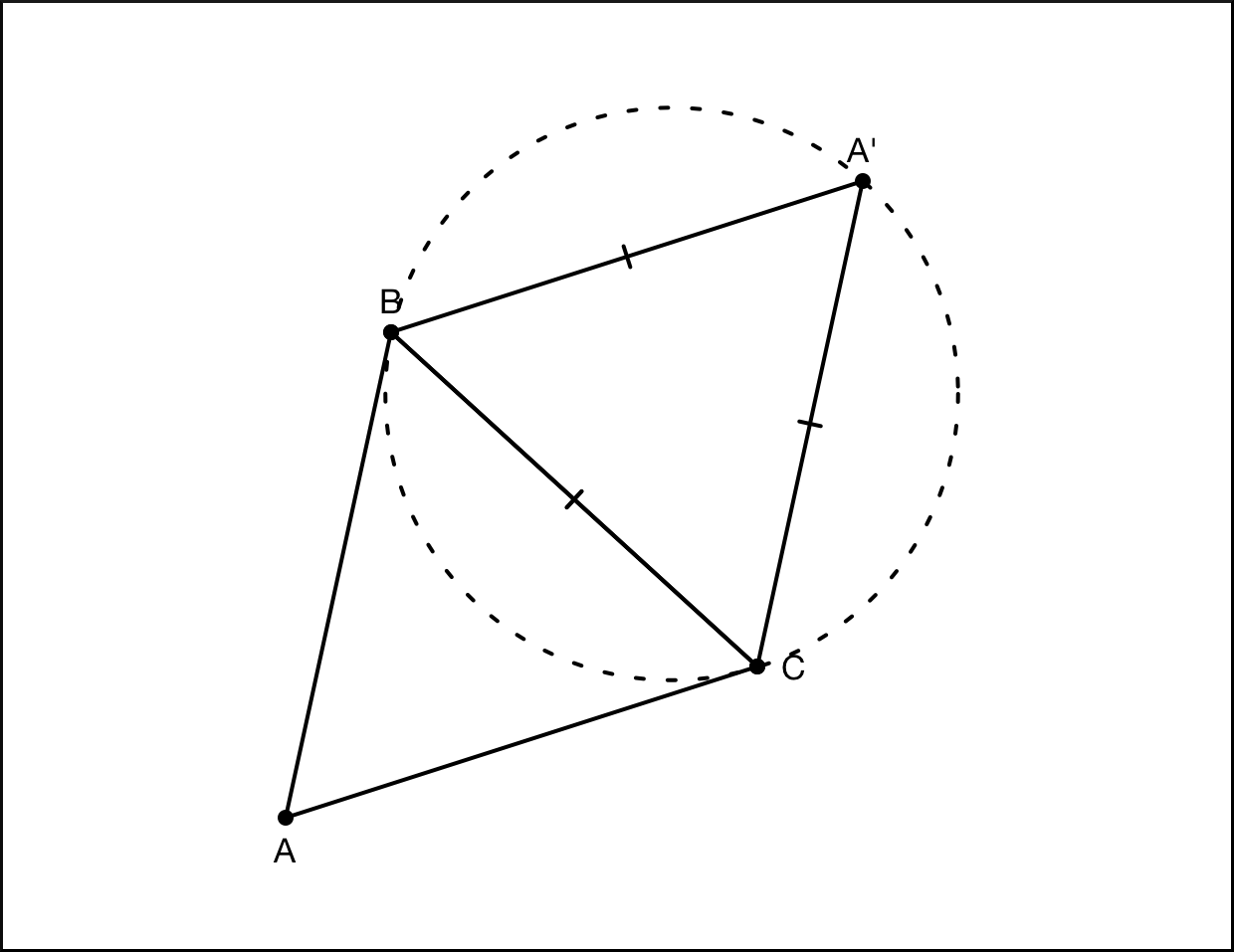
Но где именно расположить точку, чтобы все вершины были видны под углом 120°. Нужно построить еще один равносторонний треугольник, на этот раз – относительно стороны AC. И точно так же впишем его в окружность. Точка пересечения двух окружностей и будет точкой Торичелли. Мы уже определили, что угол BTC равен 120°, угол ATC получен тем же способом и также равен 120°. В сумме все три угла должны дать 360°, а значит, угол BTA также равен 120°. Таким образом, мы доказали не только существование точки Торичелли, но и то, что она может быть только одна, так как построенные нами дуги могут иметь не более одной точки пересечения. Теоретически окружности могли бы пересечься вне треугольника ABC, но случиться это могло бы только в том случае, если хотя бы один из его углов был больше 120°.
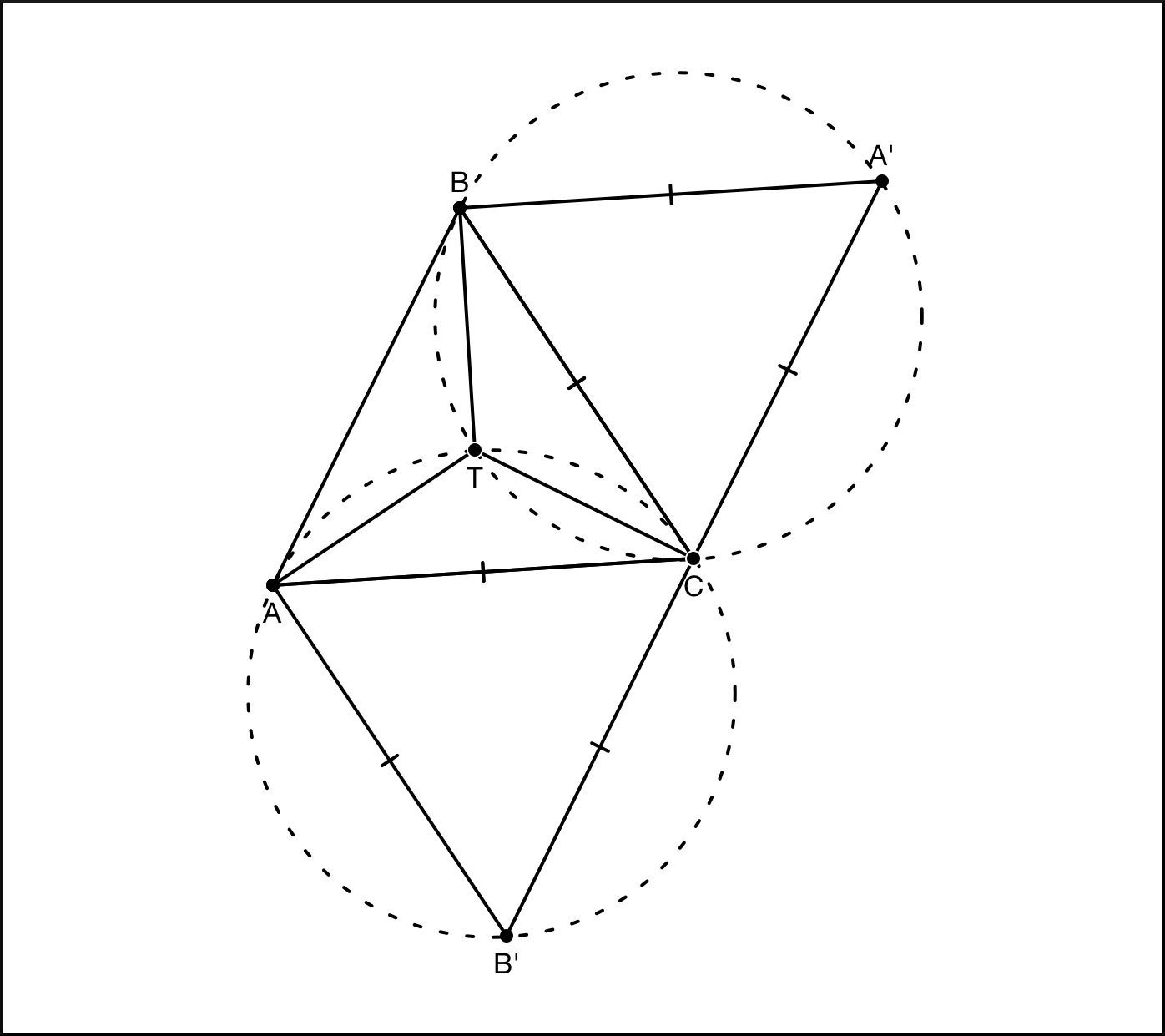
Итак, мы научились находить местоположение точки Торичелли, но так и не объяснили, почему с ее помощью можно решить задачу Штейнера о минимальной сумме расстояний до вершин треугольника. Снова возьмем треугольник ABC, где все углы будут меньше 120° и построим внешний равносторонний треугольник относительно стороны AC. Назовем его AB’C. Далее возьмем произвольную точку M на плоскости и соединим ее со всеми тремя вершинами треугольника ABC. В силу теоремы Помпею MA + MC ≥ MB’. Значит, MA + MB + MC ≥ MB’ + MB, а MB + MB’ ≥ BB’. Так как MB + MB’ не может быть меньше BB’, точка M будет иметь наименьшую сумму расстояний до вершин треугольника ABC только в том случае, когда MB + MB’ = BB’. При каких же условиях такое равенство будет верно? По теореме Помпею для этого нужно, во-первых, чтобы MA + MC было равно MB’, т.е. угол AMC должен быть равен 120°, а во-вторых, сумма отрезков BM и MB’ должна быть равна BB’, т.е. точка M должна лежать на отрезке BB’. Соответственно, углы AMB и BMC также будут равны 120°. Из всего этого следует, что MB + MB’ = BB’ только в том случае, когда точка M совпадает с точкой Торичелли. В этом и заключается решение задачи Штейнера для трех точек.

Каково же решение этой задачи для того случая, когда один из углов треугольника больше или равен 120°? Не будем подробно рассматривать доказательство для этого варианта, скажем лишь, что минимальная сумма расстояний достигается в вершине наибольшего угла треугольника. Доказать это самостоятельно несложно, нужно лишь учесть все то, что мы уже проделали выше.
Оказывается, что точка Ферма-Торичелли-Штейнера – это все, что нужно для построения систем дорог наименьшей длины. Основная задача формулируется следующим образом. На плоскости задано конечное множество (k ≥ 2) точек. Нужно соединить их кратчайшей системой дорог. Сам Штейнер решил эту задачу для k = 3 и привел некоторые примеры для k = 4. Для k ≥ 2 Штейнер даже не ставил задачи. Впервые эта задача была поставлена через 70 лет после смерти Якоба Штейнера двумя чешскими математиками Кесслером и Ярником. В 1934 году задача была опубликована в чешском математическом журнале, но первые несколько лет ей никто не интересовался. Однако в 1941 году два уже известных на тот момент американских математика Гурвиц и Курант поместили ее со ссылкой на Кесслера и Ярника в своей книге, после чего задача стала очень известной.
Досмотрев лекцию до конца, вы узнаете, как решается задача Штейнера в общем виде на плоскости и в пространстве.
