Привет! Сегодня посмотрим задачи на отрезки из 15 задания ЕГЭ по информатике.
Решим с помощью шаблона на Python и помощью рассуждений. Повторите основные логические операции в этой статье.
Покажу Вам уникальный и понятный способ для борьбы с задачами на отрезки из 15 задания ЕГЭ по информатике.
Приступим к тренировочным задачам на отрезки.
Задача (Fight)
На числовой прямой даны два отрезка B=[10; 15] и С=[20; 27]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение
¬(((x ∈ B) ∨ (x ∈ C)) ⟶ (x ∈ A))
ложно (т.е. принимает значение 0) при любом значении переменной x.
Решение:
Решение с помощью шаблона на языке Python.
Приведу собственную разработку, как можно решить задачи на отрезки из 15 задания ЕГЭ по информатике с помощью шаблона на языке Python (Питон).
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 100): for b in range(a, 100): k=0 for i in range(1, 200): x = i/2 if not( (F(10, 15, x) or F(20, 27, x)) ) or F(a, b, x): k=k+1 if k==199: mn=min(mn, b-a) print(mn)
Здесь заводим функцию F(a, b, x). Она принимает три параметра: начало отрезка a, конец отрезка b и точку x. Если точка x лежит в отрезке [a;b], то функция вернёт True, иначе False.
Затем делаем два вложенных цикла. Это поиск отрезка A. Переменная a – это начало отрезка A. Переменная b – это конец отрезка A. Для каждой точки a пробуем различные точки b, которые находится правее, чем точка a. Мы начинаем проходить переменной b со значения a, потому что в некоторых задачах длина искомого отрезка A может быть равна нулю.
Для каждого отрезка-кандидата заводим счётчик k. Прокручиваем переменную i в диапазоне от 1 до 199 включительно. А x будет крутится от 0.5 до 99.5 с шагом 0.5, тем самым имитируя фразу при любых значениях x.
Внутри “цикла i” проверяем логическое выражение. Если выражение удовлетворяет условию задачи, то прибавляем к счётчику k единицу для данного отрезка A=[a; b].
При составлении логического выражения может помочь табличка.
| Логическая операция | Представление в Питоне |
| Отрицание ¬ | not() |
| Логическое умножение ∧ | and |
| Логическое сложение ∨ | or |
| Следование A ⟶ B | not(A) or B |
| Равносильность ≡ | == |
После окончания “цикла i” проверяем счёт k. Если логическое выражение сработало при всех значениях x, то в счётчике будет число 199. Это количество итераций в “цикле i”. Если такое выполняется, то нам подходит этот отрезок A.
Среди всех отрезков A, которые удовлетворяют условию задачи, выбираем с наименьшей длиной с помощью функции min.
Примечание: У нас всегда получается отрезок A c квадратными скобками на концах A=[a, b]. Даже, если в задачке должен быть отрезок с выколотыми точками, то на длину это никак не влияет, если мы ищем минимальный отрезок, поэтому всё равно будет получатся правильный ответ. Если же мы ищем наибольшую длину, нужно получать всегда отрезок A=(a,b) c выколотыми точками. Об этот речь пойдёт ниже.
Получается 17.
Решение с помощью рассуждений.
Видим, что ко всему выражению применяется логическое отрицание. Мы можем убрать это отрицание, но тогда нужно будет сделать, чтобы выражение было истинным, а не ложным.
В подобных задачах идём от обратного. Нам нужно найти, когда выражение будет истинным, но мы исследуем случай, когда выражение будет стремится ко лжи.

Найдём, при каких значениях x левое выражение будет выдавать 1.
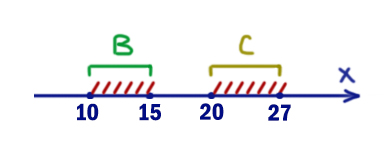
Здесь заштрихованы те иксы, которые приводят к тому, что левое выражение выдаёт 1. Это опасные x. Они “приближают” всё выражение к нулю.
Наша задача этого не допустить. У нас есть только один инструмент: подобрать такой отрезок A, чтобы правое выражение при опасных иксах выдавало 1. Тогда мы получим желаемый результат.
Т.е. при опасных иксах правое выражение должно выдавать 1. Чтобы покрыть все иксы приходится брать отрезок A=[10, 27].
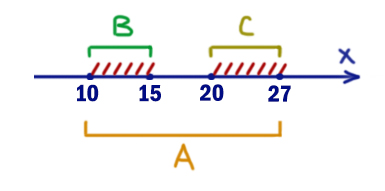
В ответе напишем длину отрезка A: 27 – 10 = 17. Здесь достаточно из наибольшей точки отнять наименьшую.
Ответ: 17
Задача (Раунд 2)
На числовой прямой даны два отрезка: B = [14; 20] и С = [15; 27]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение
¬(x ∈ A) ⟶ ((x ∈ B) ≡ (x ∈ C))
истинно (т.е. принимает значение 1) при любом значении переменной x.
Решение:
Решение с помощью шаблона на языке Python.
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 100): for b in range(a, 100): k=0 for i in range(1, 200): x=i/2 if F(a, b, x) or (F(14, 20, x) == F(15, 27, x)): k=k+1 if k==199: mn=min(mn, b-a) print(mn)
Получается ответ 13.
Решение с помощью рассуждений.
“Главной скрипкой” логического выражение является следование. Именно эта операция соединяет большие блоки логического выражения.
Нас будет интересовать тот случай, когда логическое выражение, наоборот, будет стремится к 0. Тогда правое логическое подвыражение должно равняться 0, а с помощью левого подвыражения, где находится отрезок A, мы будем исправлять ситуацию.

Заштрихуем те значения x, при которых правое подвыражение даёт ноль. Равносильность даёт ноль, когда два выражения имеют разные значения. Т.е. если x находится в одном отрезке, то в другом отрезке его не должно быть.
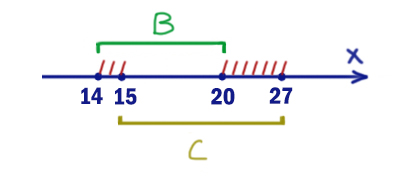
В подобных задачах можно не обращать внимание на закрашенные и выколотые точки на концах отрезков, потому что в дальнейшем нужно найти длину отрезка A, а длина от этого не зависит. Поэтому пишем и рисуем отрезки с некоторым приближением до одной точки.
Получаются два отрезка [14; 15) и (20; 27]. Это и есть “опасные” значения x. При этих значениях выражение уже “наполовину” ложно. Но с помощью A мы не дадим превратится ему в 0 при любых иксах.
Если левое подвыражение будет равно 1 при опасных значениях икс, то как раз получится то, что нам не нужно. Поэтому при опасных значениях иск, в левом выражении должен быть ноль.
Т.к. там стоит отрицание, убрав его, можно сказать, что в левом подвыражении должна стоять 1 при опасных значениях икс.
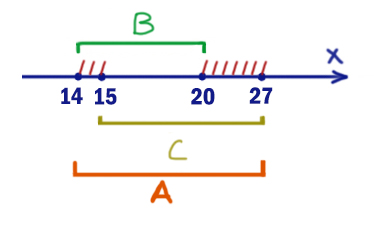
Чтобы покрыть все два отрезка опасных значений, выбираем A=[14; 27]. Нас просили найти минимальный отрезок A. Меньше не можем взять, т.к. тогда не все заштрихованные иксы будут закрыты.
Длина получается 27 – 14 = 13.
Ответ: 13
Задача (Отрезок максимальной длины)
На числовой прямой даны два отрезка: P = [43; 49] и Q = [44; 53]. Укажите наибольшую возможную длину такого отрезка A, что формула
((x ∈ A) → (x ∈ P)) ∨ (x ∈ Q)
тождественно истинна, то есть принимает значение 1 при любых x.
Решение:
Решение с помощью шаблона на языке Python.
def F(a, b, x): if a <= x <= b: return True else: return False def F2(a, b, x): if a < x < b: return True else: return False mx=0 for a in range(0, 100): for b in range(a, 100): k=0 for i in range(1, 200): x=i/2 if (not(F2(a, b, x)) or F(43, 49, x)) or F(44, 53, x): k=k+1 if k==199: mx=max(mx, b-a) print(mx)
Ответ получается 10. Здесь ищем максимальный отрезок A. При поиске отрезка максимальной длины, нужно создать функцию F2, и её применять к отрезку A, чтобы получался всегда отрезок с выколотыми точками A=(a, b).
Решение с помощью рассуждений.
Главная скрипка – это логическое или. Эта логическая операция соединяет два больших выражения.
Идём от обратного. Исследуем, когда выражение будет стремится к 0.

Логическое или выдаёт ноль, когда оба выражения равны нулю.
В начале лучше разобраться с тем выражением, где нет отрезка A. Это правое подвыражение. Там должен получаться ноль. Заштрихуем те иксы, которые выдают в правом подвыражении ноль.
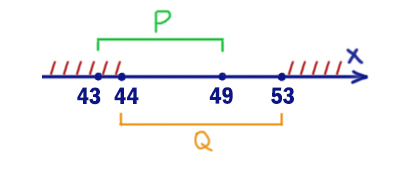
В левом выражение стоит следование. Эта операция равна нулю, когда из 1 следует 0. С помощью отрезка A мы будем спасать ситуацию. Заштрихуем, когда икс НЕ принадлежит P. Добавим это действие к предыдущей штриховке.
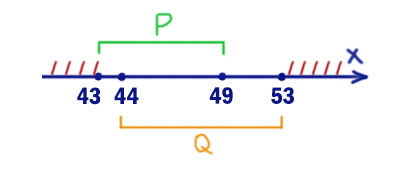
Таким образом, мы получили опасные иксы. Это все иксы, кроме отрезка [43; 53].
Именно при этих иксах выражение (x ∈ A) не должно выдавать 1. Выбираем отрезок A=[43; 53].
Мы могли бы взять отрезок и меньше, например [44; 49], но нас просили взять наибольший отрезок.
Длина равна 53 – 43 = 10.
Ответ: 10
Задача (Крепкий орешек)
На числовой прямой даны три интервала: P=[10,15], Q=[5,20] и R=(15,25]. Определите наименьшую возможную длину отрезка A, при выборе которого выражение
((x ∉ A) → (x ∈ P)) ≡ ((x ∈ Q) → (x ∈ R))
будет ложно при любых x.
Решение:
Решение с помощью шаблона на языке Python.
def F(a, b, x): if a <= x <= b: return True else: return False def F2(a, b, x): if a < x <= b: return True else: return False mn=10**9 for a in range(0, 100): for b in range(a, 100): k=0 for i in range(1, 200): x = i / 2 if not( (F(a, b, x) or F(10, 15, x)) == (not(F(5, 20, x)) or F2(15, 25, x)) ): k=k+1 if k==199: mn=min(mn, b-a) print(mn)
Здесь заводим ещё одну функцию F2 для отрезка R с выколотой левой точкой. Ответ получается 5.
Решение с помощью рассуждений.
Нужна ложь, но мы рассмотрим, когда равносильность выдаёт 1.
1) Рассмотрим первый случай 1 ≡ 1.
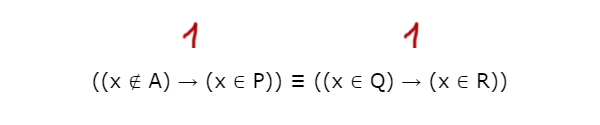
Рассмотрим левое выражение. Узнаём, когда оно выдаёт ноль, а потом сделаем инверсию, чтобы не рассматривать 3 случая.
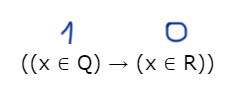
Получается, что в отрезке Q иксы должны находится, а в R нет.
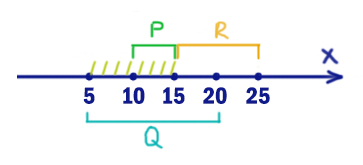
Сделаем инверсию.
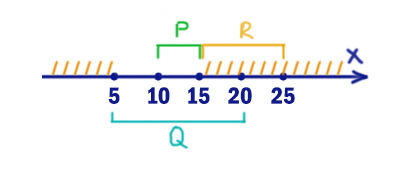
Получается интервал x ∈ (-∞ 5) U (15; ∞). Это те иксы, при которых в правом выражении будет 1.
Рассмотрим, когда левое выражение выдаёт 1.
a) 0 → 0
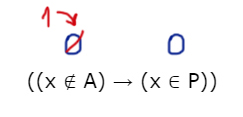
Учитывая вышеописанный интервал, понимаем, что иксы и так не лежат в отрезке P. Чтобы спаси ситуацию, нужно, чтобы выражение (x ∉ A) выдавало 1, при x ∈ (-∞ 5) U (15; ∞). Тогда левое выражение будет выдавать 0, а правое 1.
Следовательно, можем выбрать любой отрезок A в интервале [5; 15].
б) 0 → 1
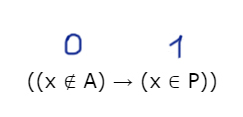
При x ∈ (-∞ 5) U (15; ∞) выражение (x ∈ P) никогда не выдаст 1. Значит, в этом варианте 1 ≡ 1 никогда не будет.
в) 1 → 1
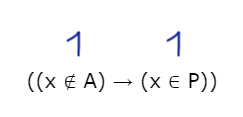
Аналогично невозможна и эта ситуация.
Перейдём ко второму случаю.
2) Рассмотрим случай 0 ≡ 0.
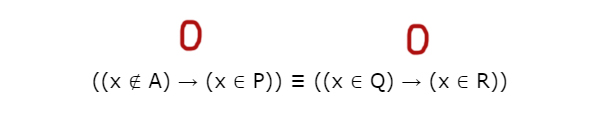
Когда правое выражение выдаёт ноль, мы уже смотрели. Это отрезок [5; 15].
Изучим те значения x, при которых левое выражение тоже будет выдавать 0 на отрезке [5; 15].
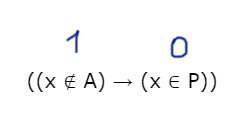
Тогда опасные иксы будут выглядеть следующим образом:
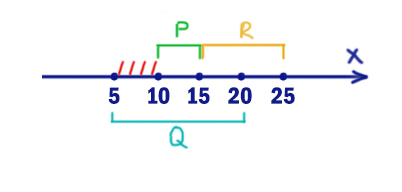
Т.е. это интервал [5; 15], но без отрезка P. Именно при x ∈ [5; 10) мы должны получать 0 в выражении (x ∉ A), чтобы спасти ситуацию. Получается A=[5;10). Меньше взять отрезок не можем, иначе не все опасные иксы будут покрыты.
Этот отрезок хорошо соотносится с первым вариантом 1) 1 ≡ 1.
Ответ получается 10 – 5 = 5.
Ответ: 5
Задача (Вперёд к победе!)
На числовой прямой даны два отрезка: D = [17; 58] и C = [29; 80]. Укажите
наименьшую возможную длину такого отрезка A, для которого логическое
выражение.
(x ∈ D) → ((¬(x ∈ C) ∧ ¬(x ∈ A)) → ¬(x ∈ D))
истинно (т.е. принимает значение 1) при любом значении переменной х.
Решение:
Решение с помощью шаблона на языке Python.
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 100): for b in range(a, 100): k=0 for i in range(1, 200): x = i / 2 if not(F(17, 58, x)) or (not((not(F(29, 80, x)) and not(F(a, b, x)))) or not(F(17, 58, x))): k=k+1 if k==199: mn=min(mn, b-a) print(mn)
Решение с помощью рассуждений.
“Главной скрипкой” данного логического выражения является следование, потому что эта операция соединяет различные логические блоки.
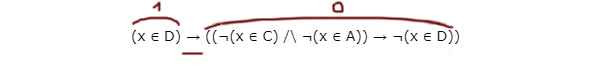
Нам нельзя допустить, чтобы первое выражение принимало 1, а второе 0, одновременно.
Рассмотрим при каких значениях x реализуется этот страшный вариант.
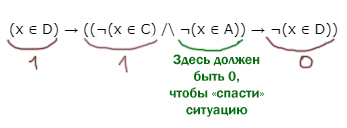
Видно, что, если левое выражение (x ∈ D) равно 1, то ¬(x ∈ D) в правой части автоматически выдаёт 0.
Чтобы умножение в правой части давало 1, необходимо, чтобы выражение ¬(x ∈ C) было истинным.
Тогда опасные значения – это отрезок D без отрезка C. Т.е., чтобы иксы были в отрезке D, но не были в отрезке С одновременно.
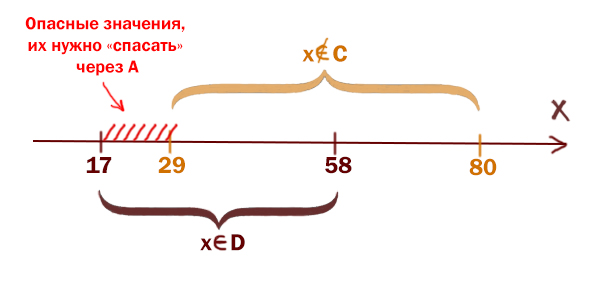
Опасные значения получаются [17; 29]. Чтобы опасный сценарий нейтрализовать, выражение ¬(x ∈ A) должно принимать значение 0. Тогда (x ∈ A) должно выдавать 1. Чтобы это происходило всегда при опасных значениях, принимаем A=[17, 29]. Длина получается 12.
Ответ: 12
Александр, а вот зачем в первой задаче учитывать вещественные x(я про деление i на 2), ведь если брать x целыми, то ответ не меняется. Это может быть критично в других задачах? И в каких случаях это повлияет на ответ?
Да, ответ может совпадать, но, например, в задаче “Крепкий орешек”, из этой статьи, уже целыми числами не обойтись
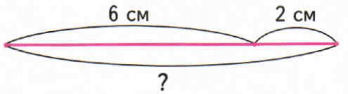
1) Сколько отрезков на этом чертеже? Как можно узнать длину самого большого отрезка?
2) Начерти отрезок длиной 10 см. Поставь на нем точку так, чтобы получился отрезок длиной 4 см. Узнай длину второго отрезка.

reshalka.com
ГДЗ учебник по математике 2 класс Моро. Часть 1. Страница 27. Номер №1
Решение 1
На чертеже 3 отрезка:
6 (см) − длина первого отрезка;
2 (см) − длина второго отрезка;
чтобы узнать длину третьего отрезка нужно сложить длины первого и второго отрезков
6 + 2 = 8 (см) − длина третьего отрезка.
Решение 2

10 − 4 = 6 (см) − длина второго отрезка.
- 06
Янв 17

Числа от 1 до 100
Сложение и вычитание
Ответы к стр. 27
1. 1) Сколько отрезков на этом чертеже? Как можно узнать длину самого большого отрезка?
На чертеже 3 отрезка.
6 + 2 = 8 (см) – длина самого большого отрезка.
2) Начерти отрезок длиной 10 см. Поставь на нём точку так, чтобы получился отрезок длиной 4 см. Узнай длину второго отрезка.
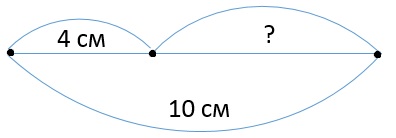
10 – 4 = 6 (см) – длина второго отрезка
2. Маше 8 лет. Мама на 20 лет старше Маши, а папа на 1 год старше мамы. Сколько лет папе?
1) 8 + 20 = 28 (л.) – маме
2) 28 + 1 = 29 (л.) – папе
О т в е т: папе 29 лет.
3. (Устно.) 1) Из суммы чисел 70 и 8 вычти число 1; 70; 8.
(70 + 8) – 1 = 77
(70 + 8) – 70 = 8
(70 + 8) – 8 = 70
2) Разность чисел 10 и 8 прибавь к числу 20; 10; 90.
(10 – 8) + 20 = 22
(10 – 8) + 10 = 12
(10 – 8) + 20 = 92
4. 12 – 8 + 9 =13 14 – 7 + 6 = 13 48 – 40 – 8 = 0
10 + 3 – 8 = 5 10 + 4 – 9 = 5 56 – 50 + 0 = 6
17 – 8 + 6 = 15 18 – 9 + 8 = 17 0 + 88 – 80 = 8
5. Узнай, на сколько миллиметров бóльшая сторона в каждом четырёхугольнике длиннее меньшей.
В синем четырёхугольнике бóльшая сторона длиннее меньшей на 2 см: 4 – 2 = 2 см
В розовом четырёхугольнике бóльшая сторона длиннее меньшей на 3 см: 5 – 2 = 3 см
6. В коробке красных и синих карандашей вместе столько, сколько зелёных. Красных карандашей 7, зелёных – 13. Сколько синих карандашей в коробке?
13 – 7 = 6 (к.)
О т в е т: 6 карандашей.
7. Составь ряд из пяти чисел по такому правилу: первое число – 2, второе – 3, а каждое следующее число равно сумме двух предыдущих.
2, 3, 5, 8, 13.
Проверочные работы, с. 10, 11.
Ответы по математике. 2 класс. Учебник.
Ответы. Учебник. Часть 1 (с. 27)
3.5 (69.46%) от 74 голосующих
Математика
6 класс
Урок № 75
Длина отрезка
Перечень рассматриваемых вопросов:
- длина отрезка;
- единицы измерения длины;
- способы измерения длины отрезка;
- решение задач на вычисление длины отрезка.
Тезаурус
Отрезок – это часть прямой, ограниченная двумя точками.
Длина отрезка – это расстояние между его концами.
Измерение длины отрезка – это сравнение длины отрезка с выбранной единицей измерения.
Длиной отрезка называется положительная величина, определённая для каждого отрезка.
Любой отрезок имеет определённую длину, большую нуля.
Обязательная литература:
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Что такое отрезок?
Отрезок – это часть прямой, ограниченная двумя точками.

Как отрезки обозначаются на чертежах?
Отрезок можно обозначить двумя заглавными буквами – отрезок АВ. Или можно обозначить отрезок одной строчной буквой – отрезок с.
Любой отрезок имеет определённую длину, большую нуля.

Длина может быть выражена натуральным или дробным числом.

Измерить отрезок – значит найти его длину.
Длина отрезка – это расстояние между его концами.
Свойства длин отрезков:
– равные отрезки имеют равные длины;
– если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей.

Эти свойства длины отрезка используются при её измерении. Чтобы измерить длину отрезка, нужно выбрать единицу длины.
Такой единицей может быть длина произвольного отрезка. В мультфильме «38 попугаев» герои измеряли длину удава в попугаях.

Для определения длины отрезка надо узнать, сколько раз в данном отрезке помещается выбранная единица измерения.
Можно сравнивать длины отрезков, не имея под рукой линейки. Например, прикладывать к отрезкам один и тот же карандаш, ластик или использовать циркуль. Для этого нужно установить иглу в начало отрезка, провести дугу, пересекающую отрезок, затем, не меняя расстояния между иглой и карандашом циркуля, переставить иглу в точку пересечения и повторить действия.
В десятичной системе мер единицами измерения длины являются 1 мм, 1 см, 1 дм, 1 м и т. д.
Рассмотрим несколько примеров измерения длины отрезка. Измерения небольших отрезков удобно производить с помощью линейки.

Прикладываем линейку так, чтобы один конец отрезка совместился с нулём. Единичный отрезок 1 см отложился 7 раз, значит, длина отрезка АВ = 7 см.

Если единичный отрезок 1 см отложился n раз, и осталась часть меньшая 1 см, то откладываем отрезки равные 1/10 см. Длина отрезка СD = 8,7 см.
При необходимости можно продолжить откладывать по 1/100 части единичного отрезка и т. д.
Алгоритм измерения длины отрезков:
– выбрать какой-либо отрезок и принять его за единицу длины;
– от одного из концов отрезка отложить последовательно отрезки, равные единичному;
– если единичные отрезки отложились n раз и конец последнего совпал с концом измеряемого отрезка, то значение его длины равно n единиц длины;
– если отрезок или его часть меньше единичного отрезка, то нужно отложить отрезки, равные 1/10 части единичного отрезка;
– если десятые части единичного отрезка отложились ровно n раз, то длина измеряемого отрезка есть конечная десятичная дробь, в которой целая часть равна количеству целых единичных отрезков, а после запятой в разряде десятых стоит количество десятых частей единичного отрезка;
– при необходимости можно откладывать 1/100 часть единичного отрезка и т. д.
Таким образом, для каждого положительного действительного числа существует отрезок, длина которого выражается этим числом.
И для каждого положительного действительного числа существует отрезок, длина которого выражается этим числом.
На практике используют приближённое значение длин отрезков, например, с точностью 1/10 или 1/100 части единичного отрезка, но точность приближения зависит от поставленной задачи.
Рассмотрим фигуры, составленные из отрезков.
Возьмем на плоскости несколько точек и соединим их отрезками. Если никакие два из этих отрезков, имеющих общие точки, не лежат на одной прямой, то линию называют ломаной.
Отрезки, из которых состоит ломаная, называются звеньями, а концы этих отрезков – вершинами ломаной.
Длина ломаной – это сумма длин всех её звеньев.

Если концы ломаной совпадают, то такая ломаная называется замкнутой.
Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником.

Периметр многоугольника равен сумме длин всех его сторон.
Разбор заданий тренировочного модуля
Тип 1. Ввод с клавиатуры пропущенных элементов в тексте.
Впишите верный ответ.
Точка P лежит на отрезке AB. Известно, что отрезок AP больше отрезка PB на 3,6 см, а отрезок AB = 10,4 см. Найдите длину отрезка PB.

Решение:
Пусть PB = x, тогда AP = x + 3,6 см.
По условию AB = 10,4 см.
Если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей.
PB + AP = AB.
Составим и решим уравнение:
x + x + 3,6 = 10,4,
2x + 3,6 = 10,4,
2x = 10,4 – 3,6,
2x = 6,8,
x = 3,4.
Значит, длина отрезка PB = 3,4 см.
Ответ: 3,4 см.
Тип 2. Множественный выбор
Выберите верные ответы.
Задача 2
Известно, что отрезок AС = 3,6 см, а отрезок BС = 7,5 см. Найдите длину отрезка АB, если все три точки лежат на одной прямой.
Варианты ответов: 3,9; 11,1; 4,8; 13,2; 16,5; 2,9.
Первый вариант решения

В этом случае АВ = АС + ВС = 3,6 + 7,5 = 11,1 (см).
Второй вариант

BC = AB + AC,
АВ = ВС – АС = 7,5 – 3,6 = 3,9 (см).
Значит, длина отрезка АВ может быть равна 11,1 см или 3,9 см. Выбираем эти варианты.
Ответ: 11,1; 3,9.
Перейти к содержимому
- Ответы к учебнику Моро 2 класс 1 часть (2015 г)
- Ответы к учебнику Моро 2 класс 2 часть (2015 г)
- Главная страница
1. 1) Сколько отрезков на этом чертеже? Как можно узнать длину самого большого отрезка?

На чертеже три отрезка: 6 см, 2 см и отрезок, который состоит из суммы двух этих отрезков.
6 + 2 = 8 (см) — длина общего отрезка
Ответ: 8 см.
2) Начерти отрезок длиной 10 см. Поставь на нём точку так, чтобы получился отрезок длиной 4 см. Узнай длину второго отрезка.
![]()
10 — 4 = 6 (см) — длина второго отрезка
Ответ: 6 см.
2. Маше 8 лет. Мама на 20 лет старше Маши, а папа на 1 год старше мамы. Сколько лет папе?
1) Сколько лет маме? 8 + 20 = 28 (лет)
2) Сколько лет папе? 28 + 1 = 29 (лет)
Ответ: 29 лет.
3. (Устно.)
1) Из суммы чисел 70 и 8 вычти число 1; 70; 8.
70 + 8 = 78, 78 — 1 = 77
70 + 8 = 78, 78 — 70 = 8
70 + 8 = 78, 78 — 8 = 70
2) Разность чисел 10 и 8 прибавь к числу 20; 10; 90.
10 — 8 = 2, 20 + 2 = 22
10 — 8 = 2, 10 + 2 = 12
10 — 8 = 2, 90 + 2 = 92
4. Реши:
12 — 8 + 9 = 4 + 9 = 13
10 + 3 — 8 = 13 — 8 = 5
17 — 8 + 6 = 9 + 6 = 15
14 — 7 + 6 = 7 + 6 = 13
10 + 4 — 9 = 14 — 9 = 5
18 — 9 + 8 = 9 + 8 = 17
48 — 40 — 8 = 8 — 8 = 0
56 — 50 + 0 = 6 + 0 = 6
0 + 88 — 80 = 88 — 80 = 8
5. Узнай, на сколько миллиметров большая сторона в каждом четырёхугольнике длиннее меньшей.

Большая сторона синего четырёхугольника имеет длину 4 см, а меньшая — 2 см.
4 — 2 = 2 (см).
Большая сторона длиннее меньшей на 2 см.
Длина большей стороны розового многоугольника равна 5 см, а меньшей — 2 см.
5 — 2 = 3 (см).
Большая сторона длиннее меньшей на 3 см.
6. В коробке красных и синих карандашей вместе столько, сколько зелёных. Красных карандашей 7, зелёных — 13. Сколько синих карандашей в коробке?
По условию — красных и синих карандашей в коробке столько же, сколько и зелёных, то есть 13 (штук). То есть, если красных 7 (штук), то синих карандашей будет 13 — 7 = 6 (штук).
Ответ: в коробке 6 синих карандашей.
7. Составь ряд из пяти чисел по такому правилу: первое число — 2, второе — 3, а каждое следующее число равно сумме двух предыдущих.
Первое число: 2
Второе число: 3
Третье число: 2 + 3 = 5
Четвертое число: 3 + 5 = 8
Пятое число: 5 + 8 = 13
Проверочные работы, с. 10, 11.
- Ответы к учебнику Моро 2 класс 1 часть (2015 г)
- Ответы к учебнику Моро 2 класс 2 часть (2015 г)
- Главная страница
