|
Под действием силы в 120 Н груз массой 12 кг перемещается вверх по наклонной плоскости. Коэффициент полезного действия наклонной плоскости 45%. Чему равна длина наклонной плоскости, если ее высота 120 см?
Сначала определим полезную работу, которая совершается при подъеме данного груза на высоту 120 см = 1,2 м. Апол = mgh = 12*10*1,2 = 144 Дж. После этого используя формулу КПД найдем полную работу. КПД = Апол/Аполн *100%, Аполн = Апол*100/45 = 320 Дж. После этого можно определить длину наклонной плоскости используя формулу работы A = F*s, где s=l (длине наклонной плоскости). l = A/F = 320/120 = 2,67 м = 267 см. автор вопроса выбрал этот ответ лучшим Знаете ответ? |
Преподаватель который помогает студентам и школьникам в учёбе.
Наклонная плоскость в физике – виды, формулы и определения с примерами
Наклонная плоскость:
Перечень простых механизмов не ограничивается рычагами и блоками. Простым механизмом является также устройство, которое называют наклонной плоскостью. Это может быть любая плоскость, наклоненная под некоторым углом к горизонту. Использование наклонной плоскости дает возможность получить выигрыш в силе. В этом легко убедиться, проделав простой опыт.
К крючку динамометра прицепим брус массой 200 г и начнем равномерно поднимать вертикально вверх. Динамометр покажет силу примерно 2 Н.
Закрепим в штативе гладкую дощечку так, чтобы она была наклонена под некоторым углом к горизонту. Положим на нее брус и начнем равномерно его двигать по доске вверх. Показания динамометра будут заметно меньше, чем в первом случае. Поскольку такая доска может быть произвольной длины, то с ее помощью можно поднять груз на любую высоту. При этом действующая на тело сила будет меньшей, чем вес тела.
Наклонная плоскость дает возможность получить выигрыш в силе, зависящий от угла ее наклона.
Чем меньше высота наклонной плоскости по сравнению с ее длиной, тем большим будет выигрыш в силе. Если длину наклонной плоскости обозначить 
Для идеальной наклонной плоскости эти отношения равны:
Из формулы видно, что для выигрыша в силе нужно сделать более длинной наклонную плоскость при той же самой высоте подъема.
Свойства наклонной плоскости используются во многих сферах производственной деятельности человека. Так, когда вывозят руду с глубоких карьеров, дорогу, по которой движутся автомобили – рудовозы, прокладывают по склону котлована, постепенно поднимая ее вверх.
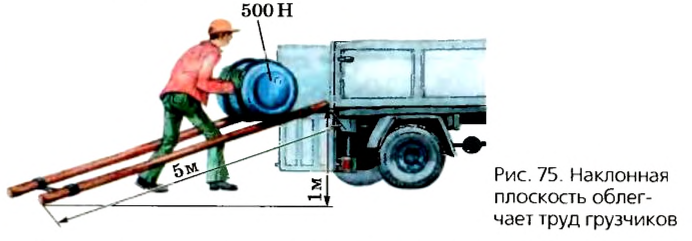
Наклонную плоскость используют и для работ по погрузке транспорта (рис. 75).
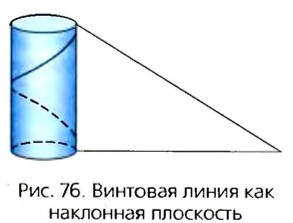
Отдельным видом наклонной плоскости является винт. Резьба, нанесенная на боковую поверхность цилиндра, образует определенный угол с его продольной осью (рис. 76), и это дает возможность получать выигрыш в силе.
За один оборот винта гайка перемещается на расстояние, равное расстоянию между двумя соседними витками. Но каждая точка гайки перемещается на длину одного витка, что значительно больше шага винта. Если шаг винта обозначить буквой  , а длину одного витка –
, а длину одного витка – 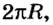 где
где 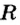 – радиус витка, то получим соотношение
– радиус витка, то получим соотношение

Винты, как правило, дают значительный выигрыш в силе, поэтому их используют в различных технических устройствах для надежного соединения деталей.
- Заказать решение задач по физике
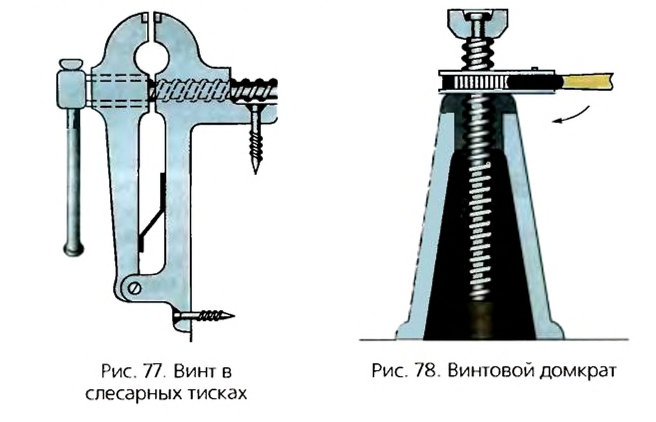
Как пример использования винта могут быть слесарные тиски. Для прокручивания винта тисков прикладывается небольшая сила, а губки тисков будут действовать на тело со значительной силой (рис. 77).
Подобным образом действует и винтовой домкрат (рис. 78).
- Давление газов и жидкостей
- Движение жидкостей и газов
- Гидравлические машины в физике
- Весовое давление жидкостей в физике
- Столкновения в физике
- Рычаг в физике
- Блоки в физике
- Движение тела под действием нескольких сил
Наталья Николаевна Пушкина
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Наклонная плоскость представляет собой плоскую поверхность, расположенную под тем или иным углом к горизонтали. Она позволяет поднять груз с меньшей силой, чем если бы этот груз поднимался вертикально вверх. На наклонной плоскости груз поднимается вдоль этой плоскости. При этом он преодолевает большее расстояние, чем если бы поднимался вертикально.
Примечание 1
Причем во сколько раз происходит выигрыш в силе, во столько раз будет больше расстояние, которое преодолеет груз.
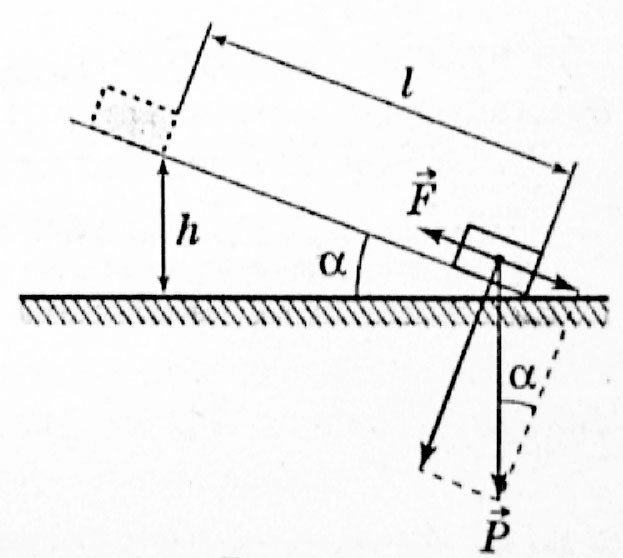
Рисунок 1. Наклонная плоскость
Если высота, на которую надо поднять груз, равна $h$, и при этом затрачивалась бы сила $F_h$, а длина наклонной плоскости $l$, и при этом затрачивается сила $F_l$, то $l$ так относится к $h$, как $F_h$ относится к $F_l$: $l/h = F_h/F_l$… Однако $F_h$ – это вес груза ($P$). Поэтому обычно записывают так: $l/h = P/F$, где $F$ – сила, поднимающая груз.
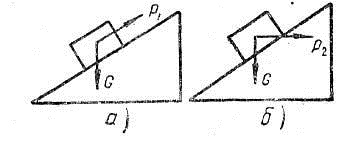
Величина силы $F$, которую надо приложить к грузу весом $Р$, чтобы тело находилось в равновесии на наклонной плоскости, равна $F_1 = Р_h/l = Рsin{mathbf alpha }$, если сила $Р$ приложена параллельно наклонной плоскости (рис.2, а), и $F_2$ = $Р_h/l = Рtg{mathbf alpha }$, если сила $Р$ приложена параллельно основанию наклонной плоскости (рис.2, б).
«Наклонная плоскость» 👇
Рисунок 2. Движение груза по наклонной плоскости
а) сила параллельна плоскости б) сила параллельна основанию
Наклонная плоскость дает выигрыш в силе, с ее помощью можно легче поднять груз на высоту. Чем меньше угол $alpha $, тем больше выигрыш в силе. Если угол $alpha $ меньше угла трения, то груз самопроизвольно не будет двигаться, и нужно усилие, чтобы тянуть его вниз.
Если учесть силы трения между грузом и наклонной плоскостью, то для $F_1$ и $F_2$ получаются следующие значения: $F_1=Рsin($${mathbf alpha }$$pm$${mathbf varphi }$)/cos${mathbf varphi }$; $F_2=Рtg($${mathbf alpha }$$pm$${mathbf varphi }$)
Знак плюс относится к передвижению вверх, знак минус – к опусканию груза. Коэффициент полезного действия наклонной плоскости ${mathbf eta }$1=sin${mathbf alpha }$cos${mathbf alpha }$/sin(${mathbf alpha }$+${mathbf varphi }$), если сила $Р$ направлена параллельно плоскости, и ${mathbf eta }$2=tg${mathbf alpha }$/tg(${mathbf alpha }$+${mathbf varphi }$), если сила $Р$ направлена параллельно основанию наклонной плоскости.
Наклонная плоскость подчиняется «золотому правилу механики». Чем меньше угол между поверхностью и наклонной плоскостью (т. е. чем она более пологая, не круто поднимающаяся вверх), тем меньше надо прикладывать сил для подъема груза, но и большее расстояние необходимо будет преодолеть.
При отсутствии сил трения выигрыш в силе $K = P/F = 1/sin$$alpha = l/h$. В реальных условиях из-за действия силы трения КПД наклонной плоскости меньше 1, выигрыш в силе меньше отношения $l/h$.
Пример 1
Груз массой 40 кг поднимают по наклонной плоскости на высоту 10 м при этом прикладывая силу 200 Н (рис.3). Какова длина наклонной плоскости? Трением пренебречь.
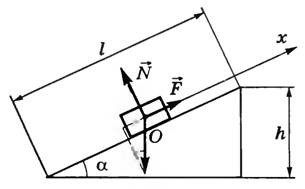
Рисунок 3
Решение
Дано:
$F$ = 200 H
$m$ = 40 кг
$H$ = 10 м
${mathbf eta }$ = 1
$g$ = 9.8 м/c2
$m$ – ?
При движении тела по наклонной плоскости отношение прилагаемой силы к весу тела равно отношению длины наклонной плоскости к её высоте: $frac{F}{P}=frac{l}{h}=frac{1}{{sin {mathbf alpha } }}$. Следовательно, $l=frac{Fh}{mg}= frac{200cdot 10}{40cdot 9,8}=5,1 м$.
Ответ: Длина наклонной плоскости 5,1 м
Пример 2
Два тела с массами $m_1$ = 10 г и $m_2$ = 15 г связаны нитью, перекинутой через неподвижный блок, установленный на наклонной плоскости (рис. 4). Плоскость образует с горизонтом угол $alpha $ = 30${}^circ$. Найти ускорение, с которым будут двигаться эти тела.
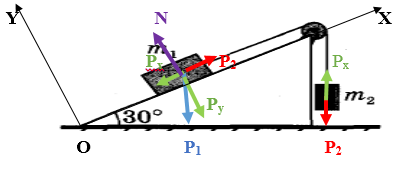
Решение
Дано:
$m_1$ = 10 Г
$m_2$ = 15 Г
${mathbf alpha }$ = 30 градусов
$g$ = 9.8 $м/c_2$
$m$ – ?
Направим ось ОХ вдоль наклонной плоскости, а ось ОY – перпендикулярно ей, и спроектируем на эти оси вектора $ {overrightarrow{Р}}_1 и {overrightarrow{Р}}_2$. Как видно из рисунка, равнодействующая сил, приложенных к каждому из тел, равна разности проекций векторов $ {overrightarrow{Р}}_1 и {overrightarrow{Р}}_2$ на ось ОХ:
[left|overrightarrow{R}right|=left|P_{2x}-P_{1x}right|=left|m_2g{sin alpha }-m_1g{sin alpha }right|=g{sin alpha left|m_2-m_1right| }] [left|overrightarrow{R}right|=9.8cdot {sin 30{}^circ }cdot left|0.015-0.01right|=0.0245 H] [a_1=frac{R}{m_1}=frac{0.0245}{0.01}=2,45frac{м}{с^2}; a_2=frac{R}{m_2}=frac{0.0245}{0.015}=1,63 м/с^2]
Ответ: Ускорения тел $a_1=2,45frac{м}{с^2}; a_2=1,63 м/с^2$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Получи верный ответ на вопрос 🏆 «Кофецент полезного действия наклоной плоскости это равно 80%. определите длину наклонай плоскасти если высота плоскасти h=40 см. И для …» по предмету 📕 Физика, используя встроенную систему поиска. Наша обширная база готовых ответов поможет тебе получить необходимые сведения!
Найти готовые ответы
Главная » Физика » Кофецент полезного действия наклоной плоскости это равно 80%. определите длину наклонай плоскасти если высота плоскасти h=40 см. И для поднятия груза массой m=50 кг требуется прекладывание паралельно плоскости силу f = 50H кофецент g=10 Н/кг
Под действием силы в 120 Н груз массой 12 кг перемещается вверх по наклонной плоскости. Коэффициент полезного действия наклонной плоскости 45%. Чему равна длина наклонной плоскости, если ее высота 120 см?
Сначала определим полезную работу, которая совершается при подъеме данного груза на высоту 120 см = 1,2 м. Апол = mgh = 12*10*1,2 = 144 Дж. После этого используя формулу КПД найдем полную работу. КПД = Апол/Аполн *100%, Аполн = Апол*100/45 = 320 Дж. После этого можно определить длину наклонной плоскости используя формулу работы A = F*s, где s=l (длине наклонной плоскости). l = A/F = 320/120 = 2,67 м = 267 см.
Примечание. Текст задачи взят с форума. Если Вы не нашли решения нужного типа задачи — пишите на форуме. Наверняка курс будет дополнен.
Задача.
| Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если наклонные относятся между собой как 1:2, а проекции наклонных равны 1 см и 7 см. | З точки до плоскості проведені дві похилі. Знайдіть довжини похилих, якщо похилі відносяться між собою як 1:2, а проекції похилих рівні 1 см і 7 див. |
Решение.
Обозначим заданную в условии точку как В. Пусть наклонные к плоскости пересекают плоскость в точках А и D .
Опустим из точки В перпендикуляр на данную плоскость. Обозначим точку пересечения перпендикуляра с плоскостью как С.
Отметим, что у нас образовались прямоугольные треугольники DBC и ABC с прямым углом C. Из чего следует, что по теореме Пифагора:
BC 2 + AC 2 = AB 2
и
BC 2 + CD 2 = BD 2
или
BC 2 = AB 2 — AC 2
и
BC 2 = BD 2 — CD 2
Теперь, учитывая, что левые части обоих выражений равны, получаем
AB 2 — AC 2 = BD 2 — CD 2
Подставим значения, которые известны по условию
AB 2 — 7 2 = BD 2 — 1
AB 2 — 49 = BD 2 — 1
Поскольку длины наклонных соотносятся как 1:2, обозначив длину BD как х (икс), получаем, что длина AB = 2x, откуда
4х 2 — 49 = х 2 — 1
3х 2 = 48
х 2 = 16
х = 4
Откуда длина второй наклонной равна 4 * 2 = 8 см
Ответ: 4 и 8 см.
Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если одна на 26 см больше другой, а проекции наклонных равны 12 см и 40 см.
Решение.
Обозначим заданную в условии точку как В. Пусть наклонные к плоскости пересекают плоскость в точках А и D .
Опустим из точки В перпендикуляр на данную плоскость. Обозначим точку пересечения перпендикуляра с плоскостью как С.
Отметим, что у нас образовались прямоугольные треугольники DBC и ABC с прямым углом C. Из чего следует, что по теореме Пифагора: BC 2 + AC 2 = AB 2
и
BC 2 + CD 2 = BD 2
или
BC 2 = AB 2 — AC 2
и
BC 2 = BD 2 — CD 2
Теперь, учитывая, что левые части обоих выражений равны, получаем
AB 2 — AC 2 = BD 2 — CD 2
Примем во внимание, что большая наклонная имеет большую проекцию.
Кроме того, поскольку одна наклонная на 26 см больше другой, то пусть BD = AB — 26.
Откуда AB = BD + 26
Подставим значения, которые известны по условию
(BD + 26) 2 — 40 2 = BD 2 — 12 2
BD 2 + 52BD + 676 — 1600 = BD 2 — 144
52BD = 780
BD = 15
Наклонная к прямой
Что такое наклонная к прямой? Сколько наклонных можно провести из одной точки к данной прямой? Как найти расстояние между основаниями наклонных?
Наклонной, проведенной из точки A к прямой a, называется отличный от перпендикуляра отрезок, соединяющий точку A с некоторой точкой на прямой a.

Рисунок наклонной, проведенной из данной точки к данной прямой, начинают с изображения перпендикуляра (даже если в условии задачи о перпендикуляре не упоминается).
Чтобы нарисовать наклонную, нужно соединить точку, из которой проводится наклонная, с любой точкой на данной прямой.
На рисунке 1 AB — перпендикуляр, проведенный из точки A к прямой a, AC — наклонная.
Точка B — основание перпендикуляра, точка C — основание наклонной AC.
Отрезок BC, соединяющий основание перпендикуляра с основанием наклонной, — проекция наклонной AC на прямую a.
Из точки к прямой можно провести бесконечно много наклонных.
Две наклонные проведенные из данной точки к данной прямой, могут быть расположены как по одну сторону от перпендикуляра, так и по разные стороны от него.
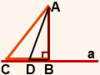
На рисунке 2 наклонные AC и AD расположены по одну сторону от перпендикуляра AB.
BC — проекция наклонной AC на прямую a,
BD — проекция наклонной AD на прямую a.
CD — расстояние между основаниями наклонных
Если наклонные расположены по одну сторону от перпендикуляра, чтобы найти расстояние между основаниями наклонных, надо найти разность между длинами их проекций.

На рисунке 3 наклонные AC и AD расположены по разные стороны от перпендикуляра AB.
BC — проекция наклонной AC на прямую a,
BD — проекция наклонной AD на прямую a.
CD — расстояние между основаниями наклонных
Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.
В следующий раз рассмотрим свойства наклонных.
2 Comments
Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.

