Как найти длину наклонной зная проекцию

Как найти стороны прямоугольного треугольника

Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• для гипотенузы (с):
  • длины катетов a и b
  • длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
  • длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
• для катета:
  • длину гипотенузы (с) и длину одного из катетов
  • длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
  • длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
  • длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
  • длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)

Введите их в соответствующие поля и получите результат.

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?

Формула

следовательно: c = √ a² + b²

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:

c = √ 3² + 4² = √ 9 + 16 = √ 25 = 5 см

Найти гипотенузу по катету и прилежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?

Формула

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:

c = 2 / cos(60) = 2 / 0.5 = 4 см

Найти гипотенузу по катету и противолежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?

Формула

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:

c = 2 / sin(30) = 2 / 0.5 = 4 см

Найти гипотенузу по двум углам

Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.

Найти катет

Найти катет по гипотенузе и катету

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:

a = √ 5² – 4² = √ 25 – 16 = √ 9 = 3 см

Найти катет по гипотенузе и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?

Формула

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:

b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см

Найти катет по гипотенузе и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:

a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см

Найти катет по второму катету и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?

Формула

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:

b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см

Найти катет по второму катету и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:

Наклонная к прямой

Что такое наклонная к прямой? Сколько наклонных можно провести из одной точки к данной прямой? Как найти расстояние между основаниями наклонных?

Наклонной, проведенной из точки A к прямой a, называется отличный от перпендикуляра отрезок, соединяющий точку A с некоторой точкой на прямой a.

Рисунок наклонной, проведенной из данной точки к данной прямой, начинают с изображения перпендикуляра (даже если в условии задачи о перпендикуляре не упоминается).

Чтобы нарисовать наклонную, нужно соединить точку, из которой проводится наклонная, с любой точкой на данной прямой.

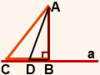
На рисунке 1 AB — перпендикуляр, проведенный из точки A к прямой a, AC — наклонная.

Точка B — основание перпендикуляра, точка C — основание наклонной AC.

Отрезок BC, соединяющий основание перпендикуляра с основанием наклонной, — проекция наклонной AC на прямую a.

Из точки к прямой можно провести бесконечно много наклонных.

Две наклонные проведенные из данной точки к данной прямой, могут быть расположены как по одну сторону от перпендикуляра, так и по разные стороны от него.

На рисунке 2 наклонные AC и AD расположены по одну сторону от перпендикуляра AB.

BC — проекция наклонной AC на прямую a,

BD — проекция наклонной AD на прямую a.

CD — расстояние между основаниями наклонных

Если наклонные расположены по одну сторону от перпендикуляра, чтобы найти расстояние между основаниями наклонных, надо найти разность между длинами их проекций.

На рисунке 3 наклонные AC и AD расположены по разные стороны от перпендикуляра AB.

BC — проекция наклонной AC на прямую a,

BD — проекция наклонной AD на прямую a.

CD — расстояние между основаниями наклонных

Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.

В следующий раз рассмотрим свойства наклонных.

2 Comments

Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c – стороны произвольного треугольника

α , β , γ – противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b – катеты

c – гипотенуза

α , β – острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b – сторона (основание)

a – равные стороны

α – углы при основании

β – угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

H – высота треугольника

a – сторона, основание

b, c – стороны

β , γ – углы при основании

p – полупериметр, p=(a+b+c)/2

R – радиус описанной окружности

S – площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

[spoiler title=”источники:”]

http://www-formula.ru/2011-10-09-11-08-41

[/spoiler]

Примечание. Текст задачи взят с форума. Если Вы не нашли решения нужного типа задачи — пишите на форуме. Наверняка курс будет дополнен.

Задача.

Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если наклонные относятся между собой как 1:2, а проекции наклонных равны 1 см и 7 см.

З точки до плоскості проведені дві похилі. Знайдіть довжини похилих, якщо похилі відносяться між собою як 1:2, а проекції похилих рівні 1 см і 7 див.

Решение.
Обозначим заданную в условии точку как В. Пусть наклонные к плоскости пересекают плоскость в точках А и D .

Опустим из точки В перпендикуляр на данную плоскость. Обозначим точку пересечения перпендикуляра с плоскостью как С.

Отметим, что у нас образовались прямоугольные треугольники DBC и ABC с прямым углом C. Из чего следует, что по теореме Пифагора:
BC 2 + AC 2 = AB 2
и
BC 2 + CD 2 = BD 2

или
BC 2 = AB 2 — AC 2
и
BC 2 = BD 2 — CD 2

Теперь, учитывая, что левые части обоих выражений равны, получаем
AB 2 — AC 2 = BD 2 — CD 2

Подставим значения, которые известны по условию
AB 2 — 7 2 = BD 2 — 1
AB 2 — 49 = BD 2 — 1

Поскольку длины наклонных соотносятся как 1:2, обозначив длину BD как х (икс), получаем, что длина AB = 2x, откуда
4х 2 — 49 = х 2 — 1
3х 2 = 48
х 2 = 16
х = 4

Откуда длина второй наклонной равна 4 * 2 = 8 см

Ответ: 4 и 8 см.

Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если одна на 26 см больше другой, а проекции наклонных равны 12 см и 40 см.

Решение.
Обозначим заданную в условии точку как В. Пусть наклонные к плоскости пересекают плоскость в точках А и D .

Опустим из точки В перпендикуляр на данную плоскость. Обозначим точку пересечения перпендикуляра с плоскостью как С.
Отметим, что у нас образовались прямоугольные треугольники DBC и ABC с прямым углом C. Из чего следует, что по теореме Пифагора: BC 2 + AC 2 = AB 2

и
BC 2 + CD 2 = BD 2

или
BC 2 = AB 2 — AC 2
и
BC 2 = BD 2 — CD 2

Теперь, учитывая, что левые части обоих выражений равны, получаем
AB 2 — AC 2 = BD 2 — CD 2

Примем во внимание, что большая наклонная имеет большую проекцию.
Кроме того, поскольку одна наклонная на 26 см больше другой, то пусть BD = AB — 26.

Откуда AB = BD + 26

Подставим значения, которые известны по условию

(BD + 26) 2 — 40 2 = BD 2 — 12 2
BD 2 + 52BD + 676 — 1600 = BD 2 — 144
52BD = 780
BD = 15

Наклонная к прямой

Что такое наклонная к прямой? Сколько наклонных можно провести из одной точки к данной прямой? Как найти расстояние между основаниями наклонных?

Наклонной, проведенной из точки A к прямой a, называется отличный от перпендикуляра отрезок, соединяющий точку A с некоторой точкой на прямой a.

Рисунок наклонной, проведенной из данной точки к данной прямой, начинают с изображения перпендикуляра (даже если в условии задачи о перпендикуляре не упоминается).

Чтобы нарисовать наклонную, нужно соединить точку, из которой проводится наклонная, с любой точкой на данной прямой.

На рисунке 1 AB — перпендикуляр, проведенный из точки A к прямой a, AC — наклонная.

Точка B — основание перпендикуляра, точка C — основание наклонной AC.

Отрезок BC, соединяющий основание перпендикуляра с основанием наклонной, — проекция наклонной AC на прямую a.

Из точки к прямой можно провести бесконечно много наклонных.

Две наклонные проведенные из данной точки к данной прямой, могут быть расположены как по одну сторону от перпендикуляра, так и по разные стороны от него.

На рисунке 2 наклонные AC и AD расположены по одну сторону от перпендикуляра AB.

BC — проекция наклонной AC на прямую a,

BD — проекция наклонной AD на прямую a.

CD — расстояние между основаниями наклонных

Если наклонные расположены по одну сторону от перпендикуляра, чтобы найти расстояние между основаниями наклонных, надо найти разность между длинами их проекций.

На рисунке 3 наклонные AC и AD расположены по разные стороны от перпендикуляра AB.

BC — проекция наклонной AC на прямую a,

BD — проекция наклонной AD на прямую a.

CD — расстояние между основаниями наклонных

Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.

В следующий раз рассмотрим свойства наклонных.

2 Comments

Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.

Теоретические материалы

Глава 9. Прямые и плоскости в пространстве

9.5. Наклонные и их проекции на плоскость. Угол наклонной с плоскостью

Прямая, пересекающая плоскость, но не перпендикулярная к ней, называется наклонной к этой плоскости.

Точка пересечения перпендикуляра (наклонной) с плоскостью называется основанием перпендикуляра (наклонной).

Отрезок, соединяющий основания наклонной и перпендикуляра, проведенных к плоскости из одной и той же точки вне ее, называется проекцией наклонной на эту плоскость.

Если из одной и той же точки, взятой вне плоскости, проведены к этой плоскости перпендикуляр и наклонные, то:
1) две наклонные, имеющие равные проекции, равны;
2) из двух наклонных та больше, проекция которой больше;
3) (обратная) равные наклонные имеют равные проекции;
4) (обратная) большей наклонной соответствует большая проекция.

Повернув прямоугольные треугольники вокруг общего их катета (перпендикуляра к плоскости) до совмещения их плоскостей, получим все наклонные (гипотенузы) и их проекции (другие катеты) в одной плоскости, где эти теоремы верны.

Перпендикуляр к плоскости меньше всякой наклонной, проведенной к той же плоскости из той же точки вне ее (катет меньше гипотенузы).

Расстоянием точки от плоскости называется длина перпендикуляра, опущенного из этой точки на данную плоскость.

Углом между наклонной и плоскостью называется острый угол между наклонной и ее проекцией на эту плоскость.

Угол между наклонной и ее проекцией на плоскость является наименьшим из всех углов, образуемых данной наклонной с прямыми, лежащими в данной плоскости.

С помощю этого онлайн калькулятора можно найти проекцию точки на заданную плоскость. Дается подробное решение с пояснениями. Для построения проекции точки на данную плоскость введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку “Решить”.

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Проекция точки на плоскость − теория, примеры и решения

Для нахождения проекции точки M на плоскость α, необходимо:

• построить прямую L, проходящую через точку M и ортогональной плоскости α.
• найти пересечение данной плоскости α с прямой L(Рис.1).

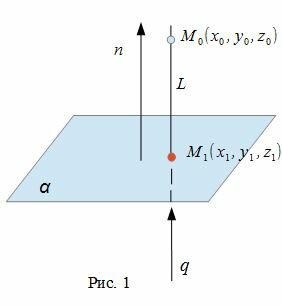
Общее уравнение плоскости имеет вид:

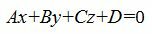(1)

где n(A,B,C)− называется нормальным вектором плоскости.

Уравнение прямой, проходящей через точку M(x, y, z) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:

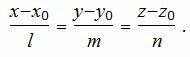(2)

Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .

Таким образом, уравнение прямой, проходящей через точку M(x, y, z) и ортогональной плоскости (1) имеет следующий вид:

(3)

Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее

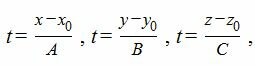
Выразим переменные x, y, z через рараметр t.

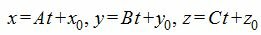(4)

Подставим значения x,y,z из выражения (4) в (1) и решим относительно t.

A(At+x)+B(Bt+y)+C(At+z)+D=0,

A 2 t+Ax+B 2 t+By+C 2 t+Cz+D=0,

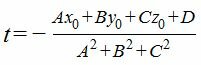(5)

Подставляя значение параметра t в выражения (4), находим проекцию M₁ точки M на плоскость (1).

Пример 1. Найти проекцию M₁ точки M(4, -3, 2) на плоскость

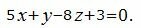(6)

Нормальный вектор плоскости имеет вид:

Подставляя координаты точки M и нормального вектора плоскости в (5), получим:

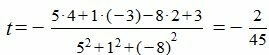(7)

Из выражений (7) находим:

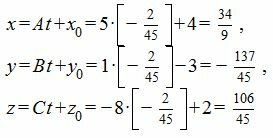
Проекцией точки M(4, -3, 2) на плоскость (6) является точка:

Проекция прямой на плоскость

Определение 1. Ортогональной проекцией точки на плоскость называют основание перпендикуляра, опущенного из этой точки на плоскость.

Рассмотрим рисунок 1, на котором изображены прямая p, перпендикулярная к плоскости α и пересекающая плоскость α в точке O.

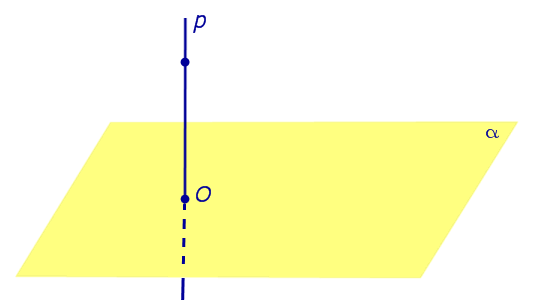
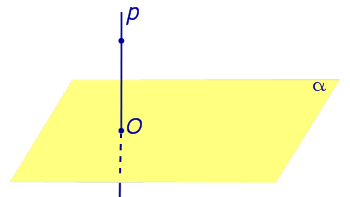
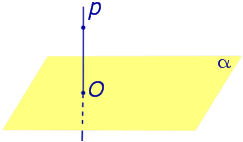
Точка O является ортогональной проекцией на плоскость α каждой точки прямой p.

Замечание 1. Рассматриваемый в данном разделе случай ортогонального проектирования точки на плоскость α представляет собой частный случай более общего понятия проектирования точки на плоскость параллельно некоторой прямой, необязательно перпендикулярной к плоскости. Такое проектирование используется в нашем справочнике при определении понятия «призма».

Замечание 2. Если это не приводит к разночтениям, для упрощения формулировок термин «ортогональная проекция на плоскость» часто сокращают до термина «проекция на плоскость».

Определение 2. Проекцией фигуры a на плоскость α называют фигуру a’, образованную проекциями всех точек фигуры a на плоскость α.

Определение 3. Прямую, пересекающую плоскость и не являющуюся перпендикуляром к плоскости, называют наклонной к этой плоскости (рис. 2).

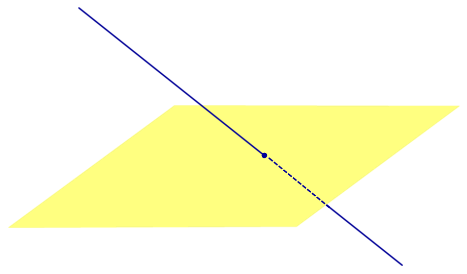
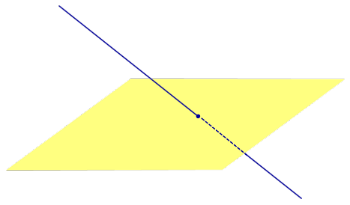
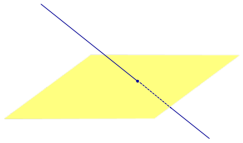
Все возможные случаи, возникающие при ортогональном проектировании прямой на плоскость представлены в следующей таблице

Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α.

На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α.

Если прямая a параллельна плоскости α , то проекцией прямой a является прямая a’, лежащая в плоскости α, параллельная прямой a и проходящая через основание O перпендикуляра PO.

Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a .

Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O , то точка O и является проекцией этой прямой на плоскость α.

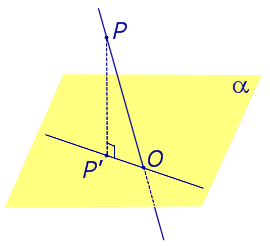
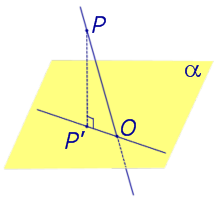
Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α.

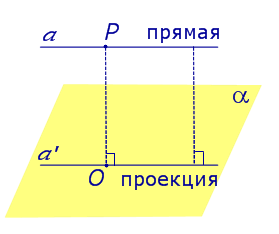
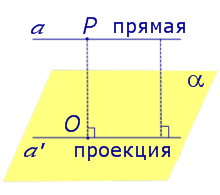
На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α.

Если прямая a параллельна плоскости α , то проекцией прямой a является прямая a’, лежащая в плоскости α, параллельная прямой a и проходящая через основание O перпендикуляра PO.

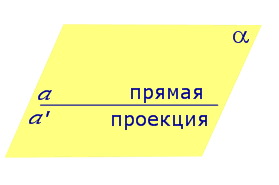
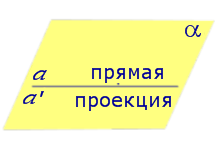
Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a .

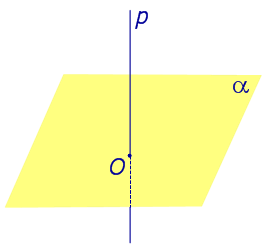
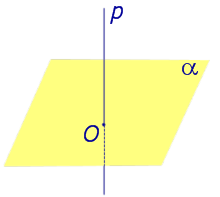
Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O , то точка O и является проекцией этой прямой на плоскость α.

Угол между прямой и плоскостью

Все возможные случаи, возникающие при определении понятия угла между прямой и плоскостью, представлены в следующей таблице.

Фигура	Рисунок	Свойство проекции
Наклонная к плоскости α
Прямая, параллельная плоскости
Прямая, лежащая на плоскости
Прямая, перпендикулярная к плоскости

Углом между наклонной к плоскости (прямая PO ) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая P’O. )

На рисунке это угол φ

Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю.

Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю.

Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным 90° ( радиан).

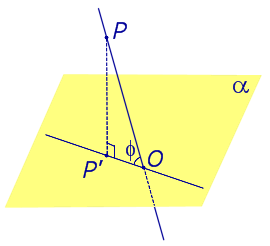
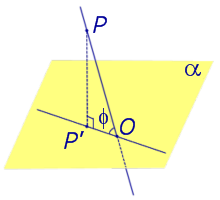
Углом между наклонной к плоскости (прямая PO ) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая P’O )

На рисунке это угол φ

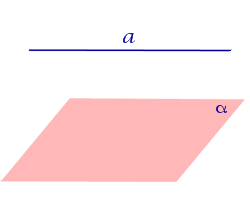
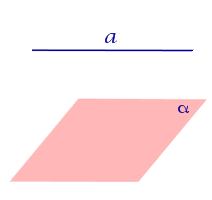
Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю.

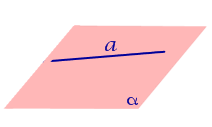
Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю.

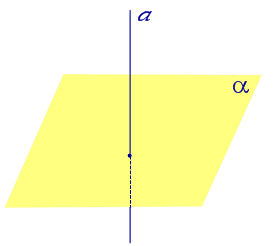
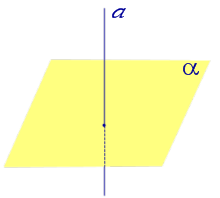
Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным 90° ( радиан).

Теорема о трех перпендикулярах

Теорема о трех перпендикулярах. Если наклонная a к плоскости α перпендикулярна к прямой b, лежащей на плоскости α, то и проекция наклонной a’ на плоскость α перпендикулярна к прямой b.

Доказательство. Рассмотрим следующий рисунок 3.

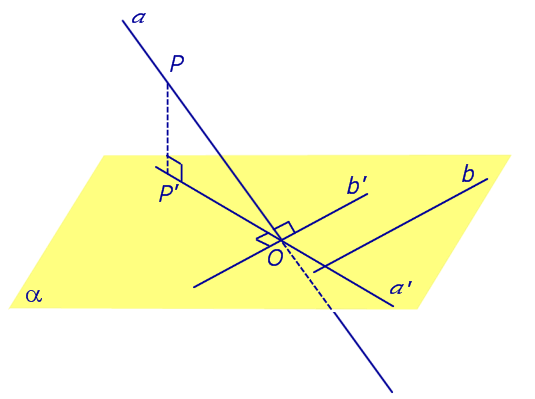
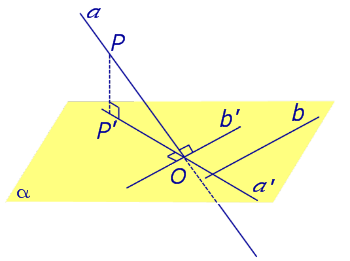
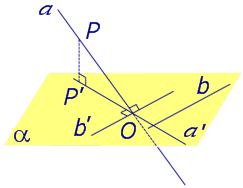
На рисунке 3 буквой O обозначена точка пересечения наклонной a с плоскостью α. Точка P – произвольная точка на прямой a, а точка P’ – это проекция точки P на плоскость α. Проведем через точку O прямую b’, параллельную прямой параллельную прямой b. Если прямая b проходит через точку O, то прямая b’, совпадет с прямой b.

Поскольку PP’ – перпендикуляр к плоскости α, то прямая PP’ перпендикулярна к прямой b’. Прямая a перпендикулярна к прямой b’ по условию. Таким образом, прямая b’ перпендикулярна к двум пересекающимся прямым PO и PP’, лежащим в плоскости POP’. В силу признака перпендикулярности прямой и плоскости получаем, что прямая b’ перпендикулярна к плоскости POP’, откуда вытекает, что прямая b’ перпендикулярна и к прямой a’, лежащей на плоскости POP’.

Теорема, обратная теореме о трех перпендикулярах. Если проекция a’ наклонной a к плоскости α перпендикулярна к прямой b, лежащей на плоскости α, то и сама наклонная a перпендикулярна к прямой b.

Доказательство. Как и для доказательства прямой теоремы о трех перпендикулярах, воспользуемся рисунком 3.

Прямая a’ перпендикулярна к прямой b по условию обратной теоремы. Прямая PP’ перпендикулярна к прямой b’, поскольку PP’ – перпендикуляр к плоскости α. Таким образом, прямая b’, перпендикулярна к двум пересекающимся прямым P’O и PP’, лежащим в плоскости POP’. В силу признака перпендикулярности прямой и плоскости прямая b’ перпендикулярна к плоскости POP’. Тогда, в частности, прямая b’ перпендикулярна к прямой a, лежащей на плоскости POP’.

Фигура	Рисунок	Определение
Наклонная к плоскости α
Прямая, параллельная плоскости
Прямая, лежащая на плоскости
Прямая, перпендикулярная к плоскости