Как найти длину направляющие косинусы вектора

Направляющие косинусы вектора.

Навигация по странице:

• Определение направляющих косинусов
• Формулы для направляющих косинусов
  • для плоских задач
  • для пространственных задач
• Примеры задач с направляющими косинусами вектора
  • плоские задачи
  • пространственные задачи

Определение направляющих косинусов

Определение. Направляющие косинусы вектора a – это косинусы углов, которые вектор образует с положительными полуосями координат.

Направляющие косинусы однозначно задают направление вектора.

Основное соотношение. Чтобы найти направляющие косинусы вектора a необходимо соответствующие координаты вектора поделить на модуль вектора.

Соответственно, координаты единичного вектора равны его направляющим косинусам.

Свойство направляющих косинусов. Сумма квадратов направляющих косинусов равна единице.

Формулы вычисления направляющих косинусов вектора

Формула вычисления направляющих косинусов вектора для плоских задач

В случае плоской задачи (рис. 1) направляющие косинусы вектора a = {a_x ; a_y} можно найти воспользовавшись следующей формулой

cos α =	ax	;	cos β =	ay
|a|	|a|

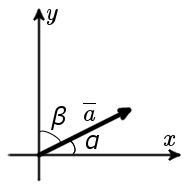рис. 1

Формула вычисления направляющих косинусов вектора для пространственных задач

В случае пространственной задачи (рис. 2) направляющие косинусы вектора a = {a_x ; a_y ; a_z} можно найти воспользовавшись следующей формулой

cos α =	ax	;	cos β =	ay	;	cos γ =	az
|a|	|a|	|a|

Свойство:

cos² α + cos² β + cos² γ = 1

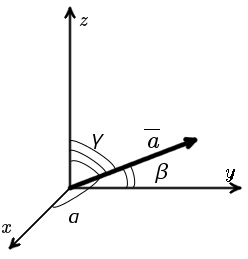рис. 2

Примеры задач с направляющими косинусами вектора

Примеры плоских задач с направляющими косинусами вектора

Пример 1. Найти направляющие косинусы вектора a = {3; 4}.

Решение:

Найдем модуль вектора a:
|a| = √3² + 4² = √9 + 16 = √25 = 5.

Найдем направляющие косинусы вектора a:

cos α =	ax	=	3	= 0.6
|a|	5

cos β =	ay	=	4	= 0.8
|a|	5

Ответ: направляющие косинусы вектора cos α = 0.6, cos β = 0.8.

Пример 2. Найти значение векора a если его длина равна 26, а направляющие косинусы cos α = 5/13, cos β = -12/13.

Решение:

a_x = |a| · cos α = 26 ·

513

= 10
a_y = |a| · cos β = 26 · (-

1213

) = -24

Ответ: a = {10; -24}.

Примеры пространственных задач с направляющими косинусами вектора

Пример 3. Найти направляющие косинусы вектора a = {2; 4; 4}.

Решение:

Найдем модуль вектора a:
|a| = √2² + 4² + 4² = √4 + 16 + 16 = √36 = 6.

Найдем направляющие косинусы вектора a:

cos α =	ax	=	2	=	1
|a|	6	3

cos β =	ay	=	4	=	2
|a|	6	3

cos γ =	az	=	4	=	2
|a|	6	3

Ответ: направляющие косинусы вектора cos α = 13, cos β = 23, cos γ = 23.

Содержание:

• Формула
• Примеры вычисления направляющих косинусов вектора

Формула

Чтобы найти направляющие косинусы вектора $bar{a}$, заданного на
плоскости своими координатами $bar{a}=left(a_{x} ; a_{y}right)$ нужно воспользоваться формулами:

$$cos alpha=frac{a_{x}}{|bar{a}|}=frac{a_{x}}{sqrt{a_{x}^{2}+a_{y}^{2}}}, quad cos beta=frac{a_{y}}{|bar{a}|}=frac{a_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}}}$$

То есть необходимо соответствующую
координату вектора поделить на его
длину.

В случае если вектор задан в пространстве $bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$, имеют место
следующие формулы для нахождения направляющих косинусов этого вектора:

$$begin{aligned} cos alpha=frac{a_{x}}{|bar{a}|}=frac{a_{x}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}} &, text { cos } beta=frac{a_{y}}{|bar{a}|}=frac{a_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}} \ cos gamma=frac{a_{z}}{|bar{a}|}=& frac{a_{z}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}} end{aligned}$$

Примеры вычисления направляющих косинусов вектора

Читать дальше: как найти угол между векторами.

Длина
вектора определяется по формуле

Направление
вектора определяется углами α, β, γ,
образованными им с осями координат Ox,
Oy, Oz. Косинусы этих углов (так
называемые направляющие
косинусы вектора)
вычисляются по формулам:

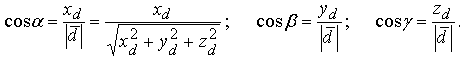
Едини́чный
ве́ктор или орт (единичный
вектор нормированного
векторного пространства) — вектор, норма (длина)
которого равна единице.

Единичный
вектор 
, коллинеарный с
заданным 
 (нормированный
вектор), определяется по формуле

.

В
качестве базисных часто
выбираются именно единичные векторы,
так как это упрощает вычисления. Такие
базисы называют нормированными.
В том случае, если эти векторы
такжеортогональны,
такой базис называется ортонормированным
базисом.

Координаты
коллинеарных
векторов удовлетворяют соотношению:

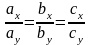
Координаты равных
векторов удовлетворяют соотношениям:

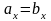
и

Координаты вектора
суммы двух
векторов удовлетворяют соотношениям:

и

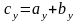
Координаты
коллинеарных
векторов удовлетворяют соотношению:

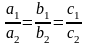
Координаты равных
векторов удовлетворяют соотношениям:

и

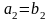
Вектор суммы
двух векторов:

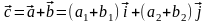
Сумма нескольких
векторов:

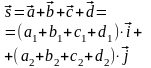
Произведение
вектора на число:

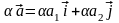
ПРОИЗВЕДЕНИЕ
ВЕКТОРА НА ЧИСЛО

Произве­дением


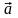
вектора

на число

называют вектор, коллинеарный вектору

,
имею­щий длину, равную

,
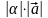
и направле­ние, совпадающее с
направлением

при >
0 и противоположное

при <
0.

СВОЙСТВА ДЕЙСТВИЙ
НАД ВЕКТОРАМИ

Операции сложения
векторов и умножения вектора на число
обладают след. свойствами:

1)

,

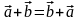
2)

,

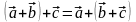
3)

,

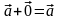
4)
,

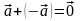
5)

,

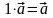
6)

,

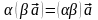
7)

,

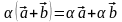
8)
.

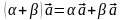
9.Выражение координат вектора через координаты его начала и конца. Расстояние между двумя точками. Деление отрезка в данном отношении. Координаты середины отрезка.

Расстояние d между
точками A(x1) и B(x2) на оси:

Расстояние d между
точками A(x1, y1) и B(x2, y2) плоскости
определяется по формуле:

Деление
отрезка в данном отношении. Если x₁ и y₁ –
координаты точки A,
а x₂ и y₂ –
координаты точки B,
то координаты x и y точки C,
делящей отрезок AB в
отношении 


,
определяются по формулам

Если 

,
то точка C(x, y)
делит отрезок AB пополам,
и тогда координаты x и y середины
отрезка AB определяются
по формулам

10. Скалярное
произведение векторов. Геометрические
свойства скалярного произведения, угол
между векторами. Условия ортогональности
векторов. Алгебраические свойства
скалярного произведения. Выражение
скаляроного произведения через
координаты множителей.

Скаля́рное
произведе́ние —
операция над двумя векторами,
результатом которой является скаляр (число),
не зависящее от системы координат и
характеризующее длины векторов-сомножителей
и угол между ними.

Скалярным
произведением в векторном
пространстве 
 над
полем 
 называется
функция 
 для
элементов 
,
принимающая значения в 
,
определенная для каждой пары элементов
и удовлетворяющая следующим условиям:

1. для
   любых трех элементов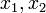 
    и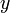 
    пространства 
    и
   любых чисел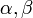 
    справедливо
   равенство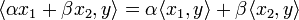 
    (линейность
   скалярного произведения по первому
   аргументу);

2. для
   любых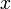 
    и 
    справедливо
   равенство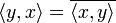 
   ,
   где черта означает комплексное
   сопряжение (эрмитова симметричность);

3. для
   любого 
    имеем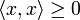 
   ,
   причем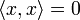 
    только
   при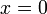 
    (положительная
   определенность скалярного произведения).

Действительное
линейное пространство со скалярным
произведением называется евклидовым,
комплексное — унитарным.

Заметим,
что из п.2 определения следует,
что 
 действительное.
Поэтому п.3 имеет смысл несмотря на
комплексные (в общем случае)
значения скалярного
произведения.

• Углом между
  двумя ненулевыми векторами евклидова
  пространства (в
  частности, евклидовой плоскости)
  называется число, косинус которого
  равен отношению скалярного произведения
  этих векторов к произведению их длин
  (норм):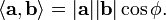

      

  Ортогональными (перпендикулярными)
  называются векторы, скалярное
  произведение которых равно нулю. Это
  определение применимо к любым
  пространствам с положительно определённым
  скалярным произведением..

11.Векторное
произведение векторов. Геометрические
приложения векторного произведения.
Условие коллинеарности векторов.
Алгебраические свойства смешанного
произведения. Выражение векторного
произведения через координаты множителей.

       Векторным
произведением вектора а на
вектор b называется
вектор с,
который:

1.
Перпендикулярен векторам a и b,
т. е. с^а и с^b;

2. Имеет
длину, численно равную площади
параллелограмма, построенного на
векторах а и b как
на сторонах (см. рис. 17), т. е. 

3.Векторы a, b и с образуют
правую тройку.

Геометрические
приложения:

Установление
коллинеарности векторов

Нахождение
площади параллелограмма и треугольника

Согласно
определению векторного произведения
векторов а и b |а хb |
= |а|
* |b |sing ,
т. е. S _пар =
|а х b |.
И, значит, DS =1/2|а х b |.

Определение
момента силы относительно точки

Из
физики известно, что моментом
силы F относительно
точки О называется
вектор М, который
проходит через точку О и:

1)
перпендикулярен плоскости, проходящей
через точки О,
А, В;

2)
численно равен произведению силы на
плечо

 
3)
образует правую тройку с векторами ОА и A В.

Стало
быть, М=ОА х F .

Нахождение
линейной скорости вращения

Скорость v точки
М твердого тела, вращающегося с угловой
скоростью w вокруг
неподвижной оси, определяется формулой
Эйлера v =w хr ,
где r =ОМ,
где О—некоторая неподвижная точка оси
(см. рис. 21).

  Условие
коллинеарности векторов
– необходимым и достаточным условием
коллинеарности ненулевого вектора 
 и
вектора 
 является
существование такого числа 
,
которое удовлетворяет равенству 
.

Алгебраические
свойства смешанного произведения

Смешанное
произведение векторов не изменяется
при круговой перестановке сомножителей
и изменяет знак на противоположный при
перестановке двух сомножителей, сохраняя
при этом свой модуль.

Знак
“
”
векторного умножения внутри смешанного
произведения может быть поставлен
между любыми его сомножителями.

Смешанное
произведение дистрибутивно относительно
любого его сомножителя: (например)
если 
,
то

Выражение
векторного произведения через координаты

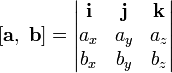
система
координат правая

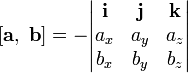
система
координат левая

12.Смешанное
произведение векторов. Геометрический
смысл смешанного произведения, условие
компланарности векторов. Алгебраические
свойства смешанного произведения.
Выражение смешанного произведения
через координаты множителей.

Смешанным
произведением упорядоченной тройки
векторов (a,b,c)  называется скалярное произведение
первого  вектора
 на векторное произведение
второго вектора на
третий.

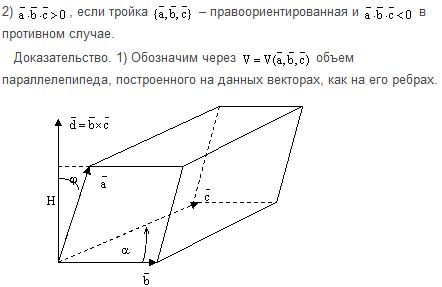
Алгебраические
свойства векторного произведения

-антикоммутативность

-ассоциативности
относительно умножения на скаляр

-дистрибутивности
по сложению

-тождество
Якоби. Выполняется в R3
и нарушается в R7

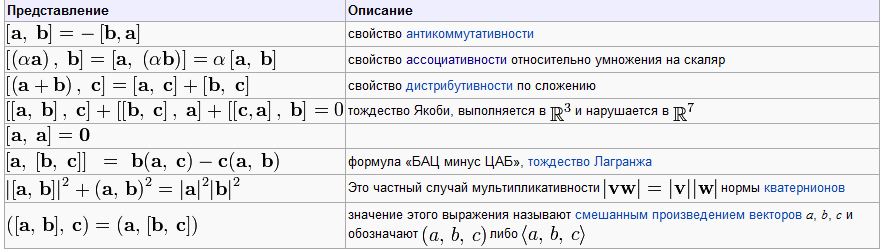
Векторные
произведения базисных векторов находятся
по определению

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Направляющие косинусы вектора.

Определение направляющих косинусов

Направляющие косинусы однозначно задают направление вектора.

Соответственно, координаты единичного вектора равны его направляющим косинусам.

Формулы вычисления направляющих косинусов вектора

Формула вычисления направляющих косинусов вектора для плоских задач

В случае плоской задачи (рис. 1) направляющие косинусы вектора a = < a_x ; a_y > можно найти воспользовавшись следующей формулой

cos α =	ax	;	cos β =	ay
| a |	| a |

рис. 1

Формула вычисления направляющих косинусов вектора для пространственных задач

В случае пространственной задачи (рис. 2) направляющие косинусы вектора a = < a_x ; a_y ; a_z > можно найти воспользовавшись следующей формулой

cos α =	ax	;	cos β =	ay	;	cos γ =	az
| a |	| a |	| a |

рис. 2

Примеры задач с направляющими косинусами вектора

Примеры плоских задач с направляющими косинусами вектора

Найдем модуль вектора a :
| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5.

Найдем направляющие косинусы вектора a :

cos α =	ax	=	3	= 0.6
| a |	5

cos β =	ay	=	4	= 0.8
| a |	5

Ответ: направляющие косинусы вектора cos α = 0.6, cos β = 0.8.

a_x = | a | · cos α = 26 · 5 13 = 10
a_y = | a | · cos β = 26 · (- 12 13 ) = -24

Примеры пространственных задач с направляющими косинусами вектора

Найдем модуль вектора a :
| a | = √ 2 2 + 4 2 + 4 2 = √ 4 + 16 + 16 = √ 36 = 6.

Найдем направляющие косинусы вектора a :

cos α =	ax	=	2	=	1
| a |	6	3

cos β =	ay	=	4	=	2
| a |	6	3

cos γ =	az	=	4	=	2
| a |	6	3

Ответ: направляющие косинусы вектора cos α = 1 3 , cos β = 2 3 , cos γ = 2 3 .

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Нахождение угла между векторами

Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.

Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →

Углом между векторами a → и b → называется угол между лучами О А и О В .

Полученный угол будем обозначать следующим образом: a → , b → ^

Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.

a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.

Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.

Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.

Нахождение угла между векторами

Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.

Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .

Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:

cos a → , b → ^ = a → , b → a → · b →

Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.

Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно – 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.

Решение

Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = – 9 3 · 6 = – 1 2 ,

Теперь определим угол между векторами: a → , b → ^ = a r c cos ( – 1 2 ) = 3 π 4

Ответ: cos a → , b → ^ = – 1 2 , a → , b → ^ = 3 π 4

Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.

Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:

cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2

А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2

Исходные данные: векторы a → = ( 2 , 0 , – 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.

Решение

1. Для решения задачи можем сразу применить формулу:

cos a → , b → ^ = 2 · 1 + 0 · 2 + ( – 1 ) · 3 2 2 + 0 2 + ( – 1 ) 2 · 1 2 + 2 2 + 3 2 = – 1 70 ⇒ a → , b → ^ = a r c cos ( – 1 70 ) = – a r c cos 1 70

1. Также можно определить угол по формуле:

cos a → , b → ^ = ( a → , b → ) a → · b → ,

но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( – 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( – 1 ) · 3 = – 1 cos a → , b → ^ = a → , b → ^ a → · b → = – 1 5 · 14 = – 1 70 ⇒ a → , b → ^ = – a r c cos 1 70

Ответ: a → , b → ^ = – a r c cos 1 70

Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.

Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , – 1 ) , B ( 3 , 2 ) , C ( 7 , – 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .

Решение

Найдем координаты векторов по координатам заданных точек A C → = ( 7 – 2 , – 2 – ( – 1 ) ) = ( 5 , – 1 ) B C → = ( 7 – 3 , – 2 – 2 ) = ( 4 , – 4 )

Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( – 1 ) · ( – 4 ) 5 2 + ( – 1 ) 2 · 4 2 + ( – 4 ) 2 = 24 26 · 32 = 3 13

Ответ: cos A C → , B C → ^ = 3 13

Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:

A B 2 = O A 2 + O B 2 – 2 · O A · O B · cos ( ∠ A O B ) ,

b → – a → 2 = a → + b → – 2 · a → · b → · cos ( a → , b → ) ^

и отсюда выведем формулу косинуса угла:

cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 – b → – a → 2 a → · b →

Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.

Хотя указанный способ имеет место быть, все же чаще применяют формулу:

Онлайн калькулятор. Направляющие косинусы вектора.

Этот онлайн калькулятор позволит вам очень просто найти направляющие косинусы вектора для плоских и пространственных задач.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление направляющих косинусов и закрепить пройденый материал.

• Калькулятор
• Инструкция
• Теория

Калькулятор для вычисления направляющих косинусов вектора

Инструкция использования калькулятора для вычисления направляющих косинусов вектора

Ввод данных в калькулятор для вычисления направляющих косинусов вектора

В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления направляющих косинусов вектора

• Между полями для ввода можно перемещаться нажимая клавиши “влево” и “вправо” на клавиатуре.

Теория. Направляющие косинусы вектора

Направляющие косинусы вектора равны отношениям координат вектора к модулю вектора.

Чтобы найти направляющие косинусы вектора a = x; a_y; a_z> необходимо соответствующие координаты вектора поделить на модуль вектора:

cos α =	ax	;	cos β =	ay	;	cos γ =	az
| a |	| a |	| a |

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/vektory/nahozhdenie-ugla-mezhdu-vektorami-primery-i-reshen/

http://0oq.ru/reshebnik-onlajn/ru.onlinemschool.com/math/assistance/vector/cos/default.htm

[/spoiler]

Перейти к содержанию