Как найти длину нормального вектора

Скалярное
произведение вектора самого на себя
называется скалярным квадратом. Эта
величина

определяет
квадрат длины вектора x.
Для обозначения длины (называемой
также нормой вектора)
используется обозначение

Например,

Рис.
16 Норма вектора

Вектор
единичной длины (||x||
= 1) называется нормированным. Ненулевой
вектор (x ≠ 0)
можно нормировать, разделив его на
длину, т.е. x =
||x||
(x/||x||)
= ||x|| e.
Здесь e =x/||x||
— нормированный вектор.

Векторы называются
ортонормированными, если все они
нормированы и попарно ортогональны.

Содержание

1.10. Угол между векторами

Скалярное
произведение определяет и угол φ
между двумя векторами x и y

Если вектора
ортогональны, то cosφ = 0 и φ = π/2, а если
они колинеарны, то cosφ = 1 и φ = 0.

Содержание 

1.11. Векторное представление матрицы

Каждую
матрицу A размера I×J можно
представить как набор векторов

Здесь
каждый вектор a_j является j-ым
столбцом, а вектор-строка b_i является i-ой
строкой матрицы A

Содержание 

1.12. Линейно зависимые векторы

Векторы
одинаковой размерности (N)
можно складывать и умножать на число,
также как матрицы. В результате получится
вектор той же размерности. Пусть имеется
несколько векторов одной
размерности x₁, x₂,…,x_K и
столько же чисел α α₁,
α₂,…,α_K.
Вектор 

y =
α₁x₁+
α₂x₂+…+
α_Kx_K  

называется линейной
комбинацией векторов x_k.

Если
существуют такие ненулевые числа α_k ≠
0, k =
1,…, K,
что y = 0,
то такой набор векторов x_k называется линейно
зависимым.
В противном случае векторы называются
линейно независимыми. Например,
векторы x₁ =
(2, 2)^t и x₂ =
(−1, −1)^t линейно
зависимы, т.к. x₁ +2x₂ = 0

Содержание 

1.13. Ранг матрицы

Рассмотрим
набор из K векторов x₁, x₂,…,x_K размерности N.
Рангом этой системы векторов называется
максимальное число линейно-независимых
векторов. Например в наборе

имеются
только два линейно независимых вектора,
например x₁ и x₂,
поэтому ее ранг равен 2. 

Очевидно,
что если векторов в наборе больше, чем
их размерность (K>N),
то они обязательно линейно зависимы. 

Рангом
матрицы (обозначается
rank(A))
называется ранг системы векторов, из
которых она состоит. Хотя любую матрицу
можно представить двумя способами
(векторы столбцы или строки), это не
влияет на величину ранга, т.к. 

rank(A)
= rank(A^t).

Содержание

1.14. Обратная матрица

Квадратная
матрица A называется
невырожденной, если она имеет
единственную обратную матрицу A^-1,
определяемую условиями

  AA⁻¹ = A⁻¹A = I.

Обратная матрица
существует не для всех матриц. Необходимым
и достаточным условием невырожденности
является 

det(A)
≠ 0 или rank(A)
= N.

Обращение матрицы
— это сложная процедура, для выполнения
которой существуют специальные программы.
Например,

Рис.
17 Обращение матрицы

Приведем формулы
для простейшего случая — матрицы 2×2

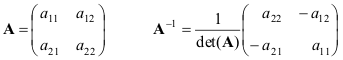
Если
матрицы A и B невырождены,
то 

(AB)⁻¹ = B⁻¹A⁻¹.

Содержание

1.15. Псевдообратная матрица

Если
матрица A вырождена
и обратная матрица не существует, то в
некоторых случаях можно
использовать псевдообратную матрицу,
которая определяется как такая матрица A⁺,
что

AA⁺A = A.

Псевдобратная
матрица — не единственная и ее вид
зависит от способа построения. Например
для прямоугольной матрицы можно
использовать метод
Мура-Пенроуза.

Если число столбцов
меньше числа строк, то 

A⁺=(A^tA)⁻¹A^t

Например, 

 

Рис.
17a Псевдообращение
матрицы

Если же число
столбцов больше числа строк, то

A⁺=A^t(AA^t)⁻¹

Содержание

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #



5.2.3. Вектор нормали плоскости (нормальный вектор)

Вектор нормали плоскости – это вектор, который перпендикулярен данной плоскости. Очевидно, что у любой плоскости бесконечно много нормальных векторов.

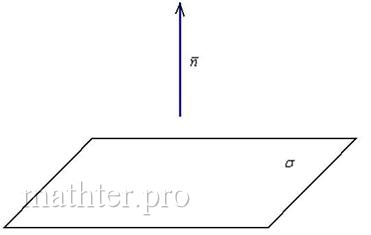
Но для решения задач нам будет хватать и одного: если плоскость задана общим уравнением  в прямоугольной (!) системе координат, то вектор  является нормальным вектором данной плоскости.

Просто до безобразия! – всё, что нужно сделать – это «снять» коэффициенты из уравнения плоскости. И чтобы хоть как-то усложнить практику рассмотрим тоже простую, но очень важную задачу, которая часто встречается, причём, не только в геометрии:

Задача 134

Найти единичный нормальный вектор плоскости .

Решение: принципиально ситуация выглядит так:

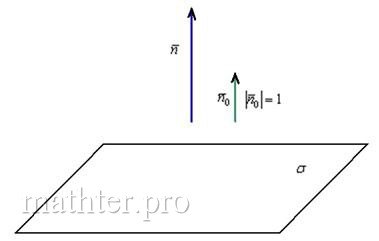
Сначала из уравнения плоскости «снимем» вектор нормали: .

И эту задачку мы уже решали: для того чтобы найти единичный вектор , нужно каждую координату вектора  разделить на длину вектора .

Вычислим длину вектора нормали:

Таким образом:

Контроль: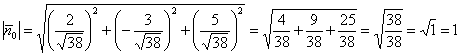, ОК

Ответ:

Вспоминаем, что координаты этого вектора  – есть в точности направляющие косинусы вектора : .

И, как говорится, обещанного три страницы ждут 🙂  – вернёмся к Задаче 130, чтобы выполнить её проверку. Напоминаю, что там требовалось построить уравнение плоскости по точке  и двум векторам , и в результате решения мы получили уравнение .

Проверяем:

Во-первых, подставим координаты точки  в полученное уравнение:

 – получено верное равенство, значит, точка  лежит в данной плоскости.

На втором шаге из уравнения плоскости «снимаем» вектор нормали: . Поскольку векторы  параллельны плоскости, а вектор  ей перпендикулярен, то должны иметь место следующие факты: . Ортогональность векторов элементарно проверяется с помощью скалярного произведения:

Вывод: уравнение плоскости найдено правильно.

В ходе проверки я фактически процитировал следующее утверждение теории: вектор  параллелен плоскости  в том и только том случае, когда .

Итак, с «выуживанием» нормального вектора разобрались, теперь ответим на противоположный вопрос:

5.2.4. Как составить уравнение плоскости по точке и вектору нормали?

5.2.2. Как составить уравнение плоскости по трём точкам?

| Оглавление |



Автор: Aлeксaндр Eмeлин

Норма (модуль, длина) вектора

В пространстве V каждому вектору x∈V ставим в соответствие некоторое неотрицательное число 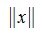так, чтобы для произвольных векторов x,y ∈V и произвольного скаляра λ выполнялись следующие условия:

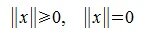1. тогда и только тогда, когда x=0.
2. .
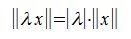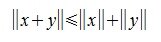3. (неравенство треугольника).

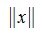называется нормой (длиной, модулем) вектора x∈V .

Примеры норм в линейных пространствах

1. max-норма, или m – норма:   

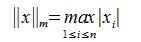
2. l-норма:    

3. Евклидова норма:    

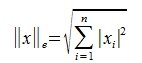
Пример вычисления нормы (длины, модуля) вектора

Вычислим нормы вектора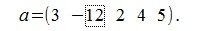

1. m-норма:

2. l-норма: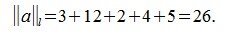

3. Евклидова норма:

  

Онлайн калькулятор для нахождения длины (нормы) вектора.
Найти нормированный вектор, норма вектора – длина вектора на линейном пространстве.
Построить вектор в двухмерном и трехмерном пространстве.