Как найти длину образующей цилиндра формула

На этой странице вы узнаете

• Как вода в кружке иллюстрирует сечение цилиндра?
• Как лист бумаги превратить в цилиндр?

Что общего у джентльмена 19 века, Вилли Вонка из «Чарли и шоколадная фабрика», Шерлока Холмса в экранизации «Безобразная невеста» и некоторых сценических костюмов? Цилиндр! О нем, вернее о фигуре цилиндра и поговорим в статье.

Понятие цилиндра

Сейчас мы говорим про мужской головной убор, который был популярен в 19 веке и стал достаточно узнаваем в массовой культуре. Оказывается, в математике также существует цилиндр. И они похожи по форме.

Цилиндр — тело вращения, полученное при вращении прямоугольника вокруг одной из его сторон. 

Возможно, для уточнения некоторых терминов вам захочется заглянуть в статью «Тела вращения». 

Если посмотреть на форму шляпы, то она действительно будет похожа на геометрическую фигуру.  Встретить цилиндр можно и в наше время. Обычная кружка является цилиндром.

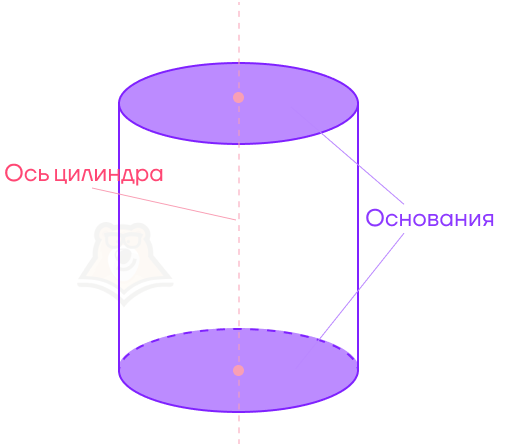
Прямая, вокруг которой мы крутили прямоугольник, чтобы получить цилиндр, — это ось цилиндра. 

Также, как у Земли есть ось вращения, она есть и у цилиндра. 

Наша кружка стоит на круглом дне. Это дно, как и самый верх кружки, будут называться основаниями цилиндра. 

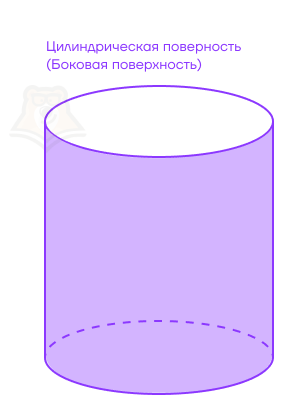
Снова посмотрим на стенки кружки. В цилиндре эта поверхность будет называться цилиндрической поверхностью. Ее также могут называть боковой поверхностью цилиндра. 

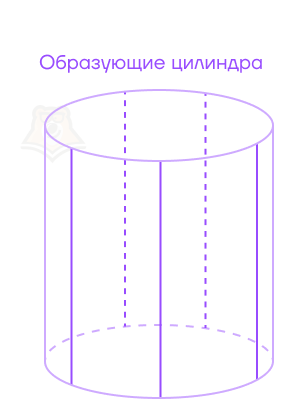
Представим, что наша кружка раскрашена вертикальными линиями. Эти линии будут лежать на цилиндрической поверхности и перпендикулярны основаниям. У них есть название:

Образующая цилиндра — отрезок, соединяющий точки окружностей основания и перпендикулярный плоскостям оснований. 

Все образующие, — а в цилиндре их очень-очень много, —лежат только на цилиндрической поверхности. Эта поверхность и состоит из множества образующих. 

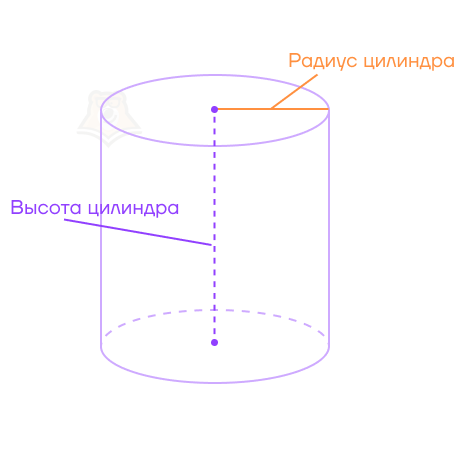
Узнаем ширину кружки. Для этого нужно измерить радиус дна. Этот же радиус будет радиусом основания, а в цилиндре он называется радиусом цилиндра. 

Теперь найдем высоту кружки. Для этого нужно измерить расстояние от дна до самого верха кружки. 

В математике это будет расстоянием между плоскостями, а ищется оно как длина перпендикуляра, опущенного из одной плоскости на другую. Подробнее про это можно прочесть в статье «Расстояния между фигурами». 

Высота цилиндра — перпендикуляр, опущенный из плоскости одного основания на плоскость второго основания. 

Свойства цилиндра

Рассмотрим, какими свойствами обладает цилиндр. 

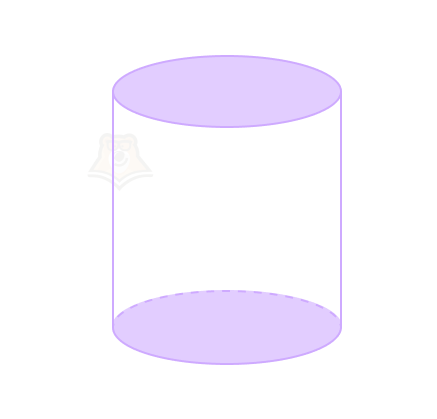
Свойство 1. Основания цилиндра равны и параллельны. 

Это всегда два равных круга, лежащих в параллельных плоскостях. 

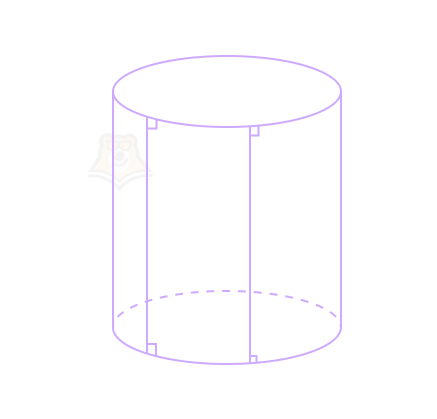
Свойство 2. Образующие цилиндра равны и параллельны. 

Поскольку все образующие перпендикулярны основаниям, то они параллельны между собой по свойству прямой и перпендикулярной ей плоскости. Подробнее про это свойство можно прочесть в статье «Углы в пространстве». 

А равны они потому, что являются перпендикуляром к основаниям, то есть равны высоте цилиндра.

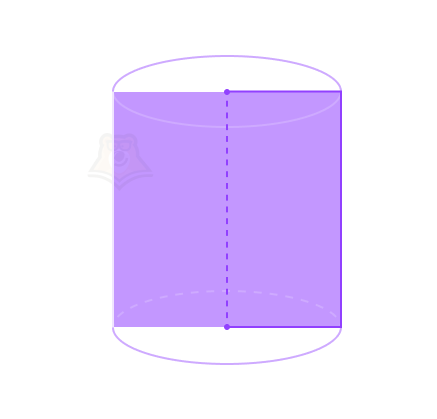
Свойство 3. Сечение цилиндра, проходящее через ось цилиндра, является прямоугольником. Такое сечение в цилиндре будет называться осевым сечением цилиндра. 

Например, если разрезать тортик по диаметру, то место среза как раз будет прямоугольником. 

Подробности про сечения фигур можно найти в статье «Сечения». 

Свойство 4. Сечение цилиндра, проходящее параллельно оси цилиндра и перпендикулярно его основаниям, будет являться прямоугольником. 

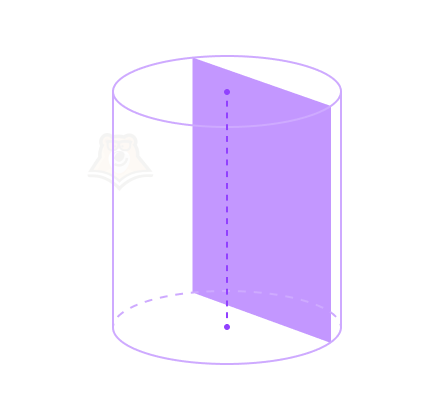
Свойство 5. Сечение цилиндра, перпендикулярное оси цилиндра, является кругом с радиусом, равным радиусу цилиндра. Такое сечение в цилиндре называется перпендикулярным сечением цилиндра. 

Заметим, что все вышеописанные свойства относятся к прямому цилиндру. 

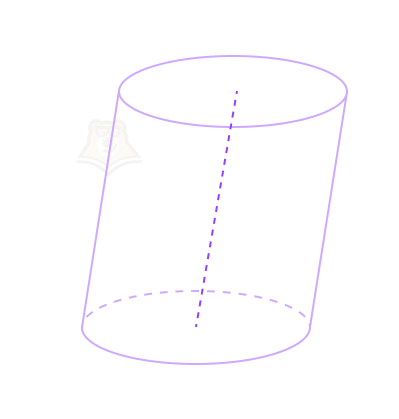
Цилиндр также может быть наклонным. В этом случае ось цилиндра и его образующие не будут перпендикулярны основаниям. 

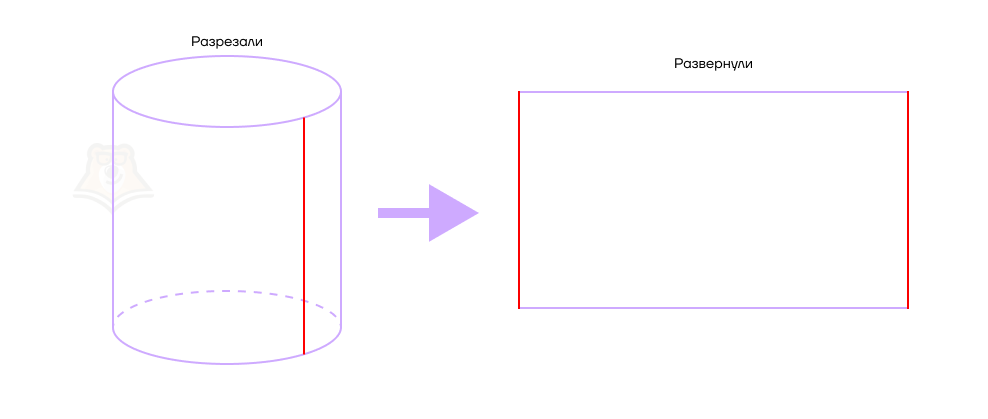
Если мы разрежем поверхность цилиндра по одной из его образующих и как бы “развернем” ее, у нас получится прямоугольник. 

Это также легко увидеть, если вспомнить художников с тубусами. Тубус имеет форму цилиндра, и свернутый прямоугольный лист принимает такую же форму. 

Развертка боковой поверхности цилиндра — прямоугольник, одна сторона которого равна высоте цилиндра, а вторая — длине окружности его основания. 

Формулы цилиндра

А если это прямоугольник, то мы знаем, как найти его площадь. Нам нужно умножить его длину на высоту. Так мы получаем площадь боковой поверхности цилиндра. 

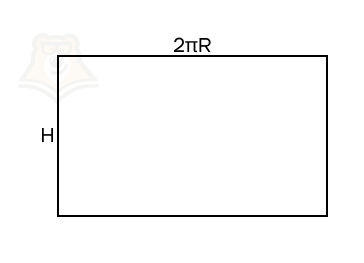
(S_{бок.} = 2 pi RH)

В этой формуле 2R — длина окружности основания, где R — его радиус, а Н — образующая (или высота) цилиндра. Подробнее про площадь прямоугольника и длину окружности (а также про площадь круга) можно прочесть в статьях «Параллелограмм» и «Окружность и круг». 

Мы нашли площадь боковой поверхности. Как же теперь найти площадь полной поверхности?

Для этого нужно сложить площади боковой поверхности и оснований. Следовательно, мы получаем следующую формулу. 

(S = S_{бок.} + 2S_{осн.} = 2 pi RH+2 pi R^2 = 2 pi R(H + R))

Допустим, мы решили сделать чашку очень вкусного чая, но чтобы правильно его заварить нам нужно знать точный объем воды. Для этого вычислим объем цилиндра. Воспользуемся следующей формулой:

(V = S_{осн.}H = pi R^2H)

В этой формуле R — радиус цилиндра, Н — высота. 

Часто формулу объема можно применить для решения жизненных задач. Например, чтобы найти объем детали, погруженной в воду. 

Пример 1. В цилиндрическом сосуде налито 1650 см³ жидкости. В этот сосуд опустили деталь. При этом уровень жидкости увеличился в 1,2 раза. Найдите объем детали. Ответ выразите в см³. 

Решение. 

Шаг 1. Выразим высоту жидкости в первый и второй раз. Пусть вначале уровень жидкости был равен х, значит после того, как в нее опустили деталь, он стал равен 1,2х. 

Шаг 2. Вспомним физику и заметим, что объем жидкости в сосуде после того, как в него опустили деталь, будет равен сумме объемов жидкости и детали: V = V_ж + V_д. 

Шаг 3. С помощью объема жидкости выразим площадь основания сосуда:

V_ж = S_осн.H
1650 = S_осн.x
(S_{осн} = frac{1650}{x})

Шаг 4. Подставим площадь основания в формулу объема жидкости после того, как в нее опустили деталь:

(V = S_{осн.}H = frac{1650}{x} * 1,2x = 1980)

Шаг 5. Тогда объем детали будет равен:

V_д = V — V_ж
V_д = 1980 — 1650 =330 

Ответ: 330 см³

Фактчек

• Цилиндр — тело вращения, полученное при вращении прямоугольника вокруг одной из его сторон. Цилиндр может быть прямым и наклонным. В наклонном цилиндре ось не перпендикулярна основаниям цилиндра. 
• Цилиндр состоит из двух оснований и цилиндрической поверхности (боковой поверхности цилиндра). Основания имеют форму кругов, равны между собой и лежат в параллельных плоскостях. Развертка боковой поверхности имеет форму прямоугольника. 
• Образующая цилиндра — отрезок, соединяющий точки окружностей основания и перпендикулярный плоскостям оснований. В прямом цилиндре образующая равна высоте цилиндра. Образующие равны и параллельны друг другу, а также образуют боковую поверхность цилиндра. 
• Осевое сечение цилиндра проходит через его ось и является прямоугольником. Любое сечение, параллельное осевому, также будет являться прямоугольником. Перпендикулярное сечение проходит перпендикулярно оси цилиндра и параллельно его основаниям. Перпендикулярное сечение имеет форму круга. 

Проверь себя

Задание 1. 
Что такое образующая цилиндра?

1. Ось вращения, с помощью которой получен цилиндр.
2. Диаметр оснований цилиндра.
3. Любой перпендикуляр, проведенный от одного основания к другому.
4. Отрезок, соединяющий точки окружности основания. 

Задание 2. 
Площадь боковой поверхности цилиндра равняется 44. Его радиус равен 8. Найдите высоту цилиндра. 

1. 2,75
2. 5,5
3. (2,75 pi)
4. 2

Задание 3. 
Площадь основания цилиндра равна 16. Его высота равна 4. Найдите площадь полной поверхности цилиндра. 

1. 64
2. (64 pi)
3. 32
4. (32 pi)

Задание 4. 
Объем цилиндра равен 28, а его высота равняется 7. Найдите диаметр основания.

1. 4
2. 2
3. 16
4. 8

Ответы: 1. – 4 2. – 1 3. – 2  4. – 1

Цили́ндр (др.-греч. κύλινδρος — валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

Связанные определения[править | править код]

• Цилиндрическая поверхность — поверхность, образуемая однопараметрическим семейством параллельных прямых (называемых образующими) и проходящими через точки некоторой кривой (называемой направляющей).
• Плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями, ограничивающими цилиндр, называются основаниями этого цилиндра.
• Часть цилиндрической поверхности, находящаяся между плоскостями оснований, называется боковой поверхностью цилиндра.
• Высотой цилиндра называется отрезок, высекаемый плоскостями его оснований на прямой, перпендикулярной им, или длина этого отрезка.

Типы цилиндров[править | править код]

• Прямым называется цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), прямая между которыми перпендикулярна плоскостям этих оснований. Данная прямая называется осью цилиндра.
• Косым называется цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), отрезок между которыми не перпендикулярен плоскостям этих оснований.
• Круговым называется цилиндр с окружностью в роли направляющей.
• Цилиндром вращения, или прямым круговым цилиндром (часто под цилиндром подразумевают именно его) называется цилиндр, который можно получить вращением (то есть тело вращения) прямоугольника вокруг одной из его сторон, содержащая которую прямая в таком случае будет осью этого цилиндра и его осью симметрии.
• Цилиндр, основания которого являются эллипсами, параболами или гиперболами, называют соответственно эллиптическим, параболическим и гиперболическим; последние два имеют бесконечный объём.
• Призма также является разновидностью цилиндра — с основанием в виде многоугольника.
• Равносторонним называется цилиндр вращения, диаметр основания которого равен его высоте^[1].

Свойства[править | править код]

• Если плоскость основания цилиндра параллельна плоскости направляющей, то граница этого основания будет по форме совпадать с направляющей кривой.

Площадь поверхности цилиндра[править | править код]

Площадь боковой поверхности[править | править код]

Площадь боковой поверхности цилиндра равна длине образующей, умноженной на периметр сечения цилиндра плоскостью, перпендикулярной образующей.

Площадь боковой поверхности прямого цилиндра вычисляется по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой и длиной , равной периметру основания. Следовательно, площадь боковой поверхности цилиндра равна площади его развёртки и вычисляется по формуле:

В частности, для прямого кругового цилиндра:

, и , здесь и далее — радиус основания цилиндра.

Для наклонного цилиндра площадь боковой поверхности равна длине образующей, умноженной на периметр сечения, перпендикулярного образующей:

Простой формулы, выражающей площадь боковой поверхности косого цилиндра через параметры основания и высоту, в отличие от объёма не существует. Для наклонного кругового цилиндра можно воспользоваться приближёнными формулами для периметра эллипса, а затем умножить полученное значение на длину образующей.

Площадь полной поверхности[править | править код]

Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований.

Для прямого кругового цилиндра:

Объём цилиндра[править | править код]

Для наклонного цилиндра существуют две формулы:

• Объём равен длине образующей, умноженной на площадь сечения цилиндра плоскостью, перпендикулярной образующей.

  ,

• Объём равен площади основания, умноженной на высоту (расстояние между плоскостями, в которых лежат основания):

  ,

где  — длина образующей, а  — угол между образующей и плоскостью основания. Для прямого цилиндра .

Для прямого цилиндра , и , и объём равен:

• 

Для кругового цилиндра:

,

где d — диаметр основания.

Примечания[править | править код]

Геометрия, 11 класса

Урок №6. Тела вращения. Цилиндр

Перечень вопросов, рассматриваемых в теме:

• тело вращения;
• цилиндрическая поверхность, её образующая; цилиндр, все его элементы и сечения;
• площади поверхностей цилиндра.

Глоссарий по теме

Цилиндрическая поверхность – это поверхность, образованная прямыми, проходящими через все точки окружности, перпендикулярными плоскости, в которой лежит эта окружность.

Эти прямые – образующие цилиндрической поверхности.

Прямая, проходящая через центр окружности, перпендикулярно к плоскости – ось цилиндрической поверхности.

Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами.

Круги – основания цилиндра; отрезки образующих, заключённые между основаниями – образующие цилиндра; образованная ими часть цилиндрической поверхности – боковая поверхность.

Ось цилиндрической поверхности называется осью цилиндра.

Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.

Сечение – изображение фигуры, образованной рассечением тела плоскостью.

Осевое сечение – вариант сечения, при котором плоскость проходит через ось тела.

Развёртка боковой поверхности цилиндра – прямоугольник, одна сторона которого равна высоте цилиндра, а другая длине окружности основания.

Основная литература:

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций: базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс.

Дополнительная литература:

Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-79.

Открытые электронные ресурсы:

Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177

Теоретический материал для самостоятельного изучения

1. Основные определения

Определение

Цилиндрической поверхностью называется поверхность, образованная прямыми, проходящими через все точки окружности, перпендикулярными плоскости, в которой лежит эта окружность (см.рис.).

Определение

Сами прямые называют образующими цилиндрической поверхности.

Определение

Прямая, проходящая через точку О, перпендикулярно к плоскости, называется осью цилиндрической поверхности.

Так как все образующие и ось перпендикулярны плоскости 𝛂, значит они параллельны друг другу (вспомнить теорему «Если две прямые перпендикулярны к плоскости, то они параллельны»).

Если построить ещё одну плоскость 𝛃, которая будет параллельна плоскости 𝛂, то отрезки образующих, заключённые между плоскостями 𝛂 и 𝛃 будут параллельны и равны друг другу (вспомнить свойство параллельных плоскостей «отрезки параллельных прямых, заключённые между параллельными плоскостями, равны»). Точки, являющиеся концами отрезков параллельных прямых и лежащие в плоскости 𝛃, дают окружность, равную окружности, лежащей в плоскости 𝛂.

Определение

Тело, ограниченное цилиндрической поверхностью и двумя кругами (границы которых есть те самые равные окружности в плоскостях 𝛂 и 𝛃) называется цилиндром.

Определение

Круги называются основаниями цилиндра, отрезки образующих, заключённые между основаниями, – образующими цилиндра, а образованная ими часть цилиндрической поверхности – боковой поверхностью цилиндра.

Определение

Ось цилиндрической поверхности называется осью цилиндра.

Определение

Длина образующей называется высотой цилиндра (все образующие равны и параллельны), а радиус основания – радиусом цилиндра.

Также цилиндр можно получить вращением прямоугольника вокруг одной из сторон. Тогда эта сторона (вокруг которой происходит вращение) будет совпадать с осью цилиндра, противоположная сторона будет образовывать боковую поверхность, а две оставшиеся стороны образуют верхнее и нижнее основания, одновременно являясь радиусами цилиндра.

2. Сечения цилиндра различными плоскостями

Пусть секущая плоскость проходит через ось цилиндра. Такое сечение называют осевым. Оно представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра.

Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.

Если секущая плоскость проходит параллельно оси цилиндра, но не содержит саму ось, то сечение является прямоугольником две стороны которого – образующие, а две другие – отрезки, соединяющие эти образующие в верхнем и в нижнем основании (ЗАМЕЧАНИЕ: эти отрезки меньше диаметров оснований цилиндра).

3. Основные формулы

Формула для вычисления площади боковой поверхности цилиндра: S_бок=2𝛑RL.

То есть площадь боковой поверхности равна произведению длины окружности основания цилиндра на его высоту.

Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. В виде формулы это можно записать так: S_полн=2𝛑R(R+L).

Примеры и разбор решения заданий тренировочного модуля

1. Дан цилиндр.

Выберите значение площади его боковой поверхности

1) 60π

2) 192π

3) 120π

4) 36π

Решение:

Площадь боковой поверхности вычисляется по формуле: S=2πRL.

R=6, L=10

Подставим: S=2π·6·10=120π.

Ответ: 3) 120π

2. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу 120⁰. Образующая цилиндра равна 6, расстояние от оси до секущей плоскости равно 1. Найдите площадь сечения.

Решение:

Сделаем чертеж:

По условию задачи ∟АОВ=120⁰, ВС= 6.

Расстояние от оси до секущей плоскости – отрезок ОН=1.

Найдем сторону АВ сечения.

∆ОНВ – прямоугольный.

В ∆ОНВ: ОН=1, ∟НОВ=60⁰.

НВ=ОН·tg60⁰=1·.

S_сеч=6·=18

Ответ: 18

3. Высота цилиндра на 6 больше его радиуса, площадь полной поверхности равна 144π. Найдите его образующую.

Решение:

S_полн =2πR(R+L)

По условию задачи L=R+6.

144π=2πR(R+R+6).

Получили квадратное уравнение относительно радиуса:

R²+6R-72=0

R=-12 или R=6. Так как длина радиуса не может быть отрицательной, получаем значение: R=6. Тогда образующая цилиндра равна 12.

Ответ: 12.

Определение цилиндра: его основание и высота, разновидности

Содержание:

• Что такое цилиндр в геометрии
• Виды цилиндров
• Как найти высоту цилиндра
• Развертка
  • Развертка боковой поверхности
  • Развертка полной поверхности

Разбираемся в особенностях трехмерного геометрического тела под названием цилиндр. Смотрим виды цилиндров, его свойства, какие бывают развертки, а также даем определения составным частям этой фигуры.

Что такое цилиндр в геометрии

Определения

Цилиндр — это трехмерное геометрическое тело, которое ограничено цилиндрической поверхностью и двумя параллельными плоскостями.

Цилиндрическая поверхность — это поверхность, которая образуется за счет движения в пространстве прямой (образующей) параллельно самой себе, пересекающей данную линию (направляющую).

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Основания — это одинаковые круги, которые ограничивают цилиндр и находятся параллельно друг другу.

Образующая — отрезок, который соединяет точки окружностей оснований цилиндра и перпендикулярный плоскостям этих оснований. Она равна высоте цилиндра или расстоянию от одного его основания до другого.

Виды цилиндров

Классификация цилиндров может быть разной в зависимости от тех или иных параметров:

• по наклону образующей;
• по форме основания.

У прямого цилиндра образующие строго перпендикулярны основаниям фигуры.

В случае, когда этот угол не равен (90^circ), цилиндр называют наклонным.

Помимо кругов, в основаниях фигуры могут быть еще и эллипсы или другие замкнутые фигуры. Однако, кроме замкнутых форм, основании цилиндру может служить и парабола, и гипербола, и любая друга открытая функция. Такой цилиндр будет называться развернутым.

Как найти высоту цилиндра

Рассмотрим варианты нахождения высоты фигуры, а также длины ее образующей (которая равна этой высоте).

• Первым делом взглянем на формулу: (V=pi R^2times H), где V — объем цилиндра, R — радиус основания, H — высота фигуры.

Через эту формулу можем выразить высоту:

(H=frac V{pi R^2})

Таким образом мы можем узнать H данного геометрического тела, если нам известен его объем и радиус. Если же вместо радиуса мы знаем диаметр, формула расчета будет выглядеть так:

(H=frac{4V}{D^2})

В случае, когда нам известен диаметр и площадь фигуры, мы так же можем найти высоту. Следует обратить внимание, что в зависимости от того, будет ли известна площадь боковой или полной поверхности, формула будет меняться.

Для расчета S боковой поверхности (часть, ограниченная цилиндрической поверхностью) цилиндра мы используем формулу:

(S=2pi RH)

выражаем H и получаем:

(H=frac S{2pi R})

Если известна S полной поверхности (включает в себя площадь оснований фигуры), используем формулу:

(S=2pi R(H+R)=2pi Rtimes H+2pi R^2)

выражаем H и получаем:

(H=frac{S-2pi R^2}{2pi R})

• Для третьего способа нужно будет провести прямоугольное сечение, ширина которого должна будет совпадать с диаметрами оснований, а длина — с образующими цилиндра.

Таким образом, получается прямоугольный треугольник САВ. А так как высота равна образующей, мы можем вычислить ее по теореме Пифагора:

(СВ^2=АС^2-АВ^2)

(H=СВ=sqrt{АС^2-АВ^2})

Развертка

Как уже было упомянуто выше, всего существует две площади поверхности цилиндра: боковой поверхности и полной поверхности. У каждой из них также есть и своя развертка. Разберемся, как они выглядят.

Развертка боковой поверхности

Легче всего представить себе развертку боковой поверхности цилиндра, посмотрев на этикетку пластиковой бутылки. Когда вы ее отклеиваете, то видите прямоугольник. То же самое и с цилиндрическим геометрическим телом: развёрткой его боковой поверхности является прямоугольник. Его длина соответствует длине окружности, лежащей в основании, а ширина — высоте самой трехмерной фигуры.

Развертка полной поверхности

Если развернуть полную поверхность цилиндра, получится примерно то же самое, только с двумя дополнительными элементами в виде окружностей оснований. Выглядит это так:

Текст с ошибкой:

Расскажите, что не так