Формула длины образующей конуса по радиусу и высоте, расчет в см
Введите радиус основания конуса в см
Введите длину образующей конуса в см:
Расчет приведен для прямого кругового конуса (подробное описание внизу страницы)
Длина образующей конуса равна:
0.00см
0.00м
Как рассчитать длину образующей прямого кругового конуса по радиусу основания и высоте?
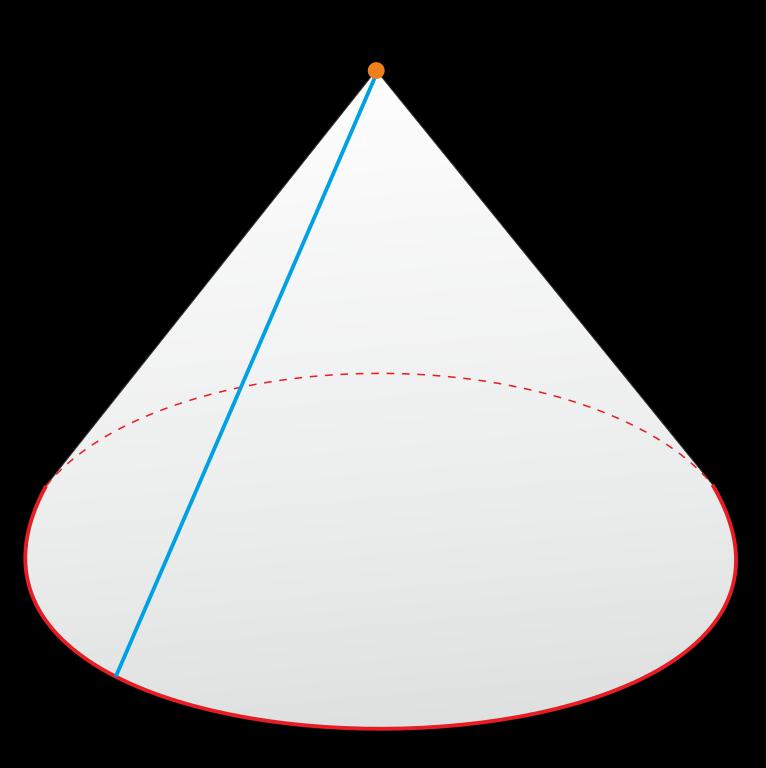
Прямой круговой конус — конус в основании которого лежит круг и центр симметрии совпадает с центром этого круга (то есть это обычный, в простом понимании, конус).
Длина образующей прямого кругового конуса вычисляется по формуле:
l = √(r2 + h2), где
h — высота конуса;
r — радиус основания конуса.
l — образующая конуса;
Квадрат длины образующей конуса равен сумме квадрата радиуса основания конуса и квадрата высоты конуса (теорема Пифагора)
Если радиус и высота конуса измерены в см (сантиметрах), то длина образующей равна:
lсм = √(r2см+ h2см)
lм = (√(r2см+ h2см))/100
Геометрия является разделом математики, изучающим структуры в пространстве и отношение между ними. В свою очередь она также состоит из разделов, и одним из них является стереометрия. Она предусматривает изучение свойств объемных фигур, находящихся в пространстве: куба, пирамиды, шара, конуса, цилиндра и др.
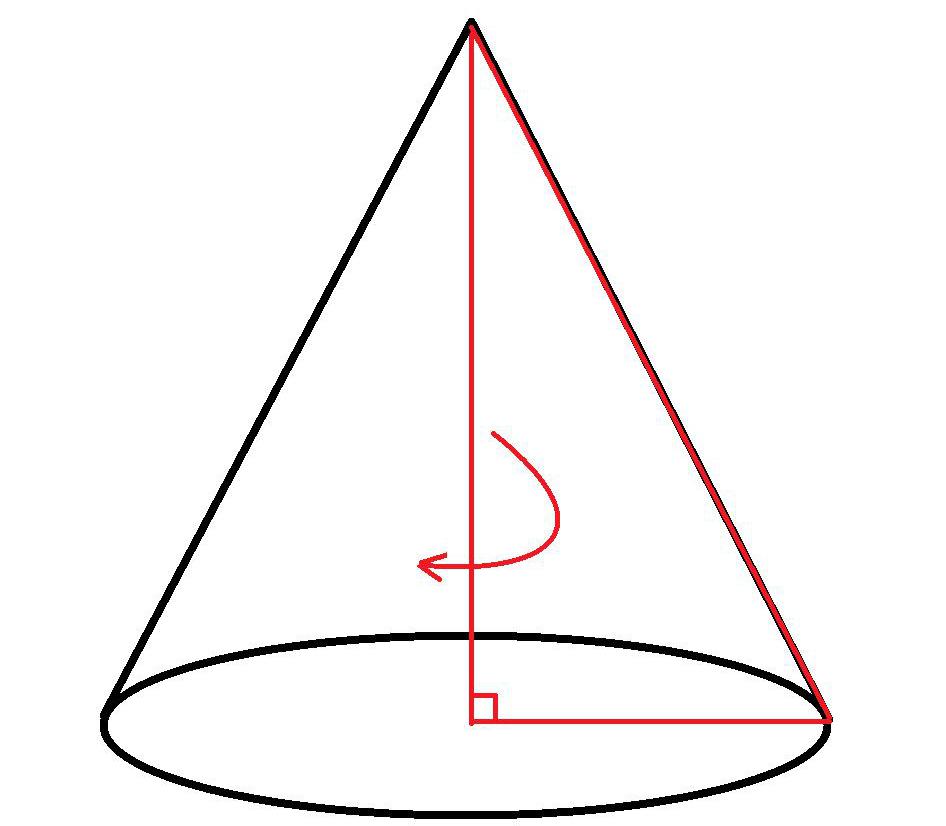
Конус – это тело в евклидовом пространстве, которое ограничивает коническая поверхность и плоскость, на которой лежат концы ее образующих. Его образование происходит в процессе вращения прямоугольного треугольника вокруг любого из его катетов, поэтому он относится к телам вращения.
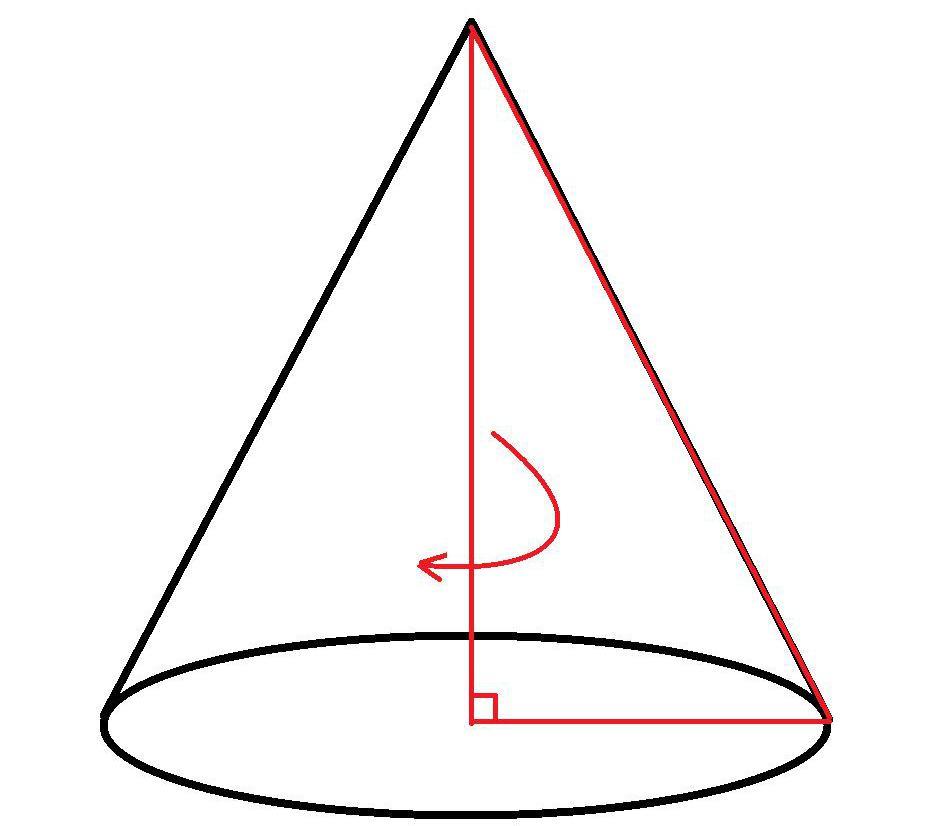
Составляющие конуса
Различают следующие виды конусов: косой (или наклонный) и прямой. Косым называется тот, ось которого пересекается с центром его основания не под прямым углом. По этой причине высота в таком конусе не совпадает с осью, так как она является отрезком, который опущен из вершины тела на плоскость его основания под углом 90°.

Тот конус, ось которого расположена перпендикулярно к его основанию, называется прямым. Ось и высота в таком геометрическом теле совпадают по причине того, что вершина в нем расположена над центром диаметра основания.
Конус состоит из следующих элементов:
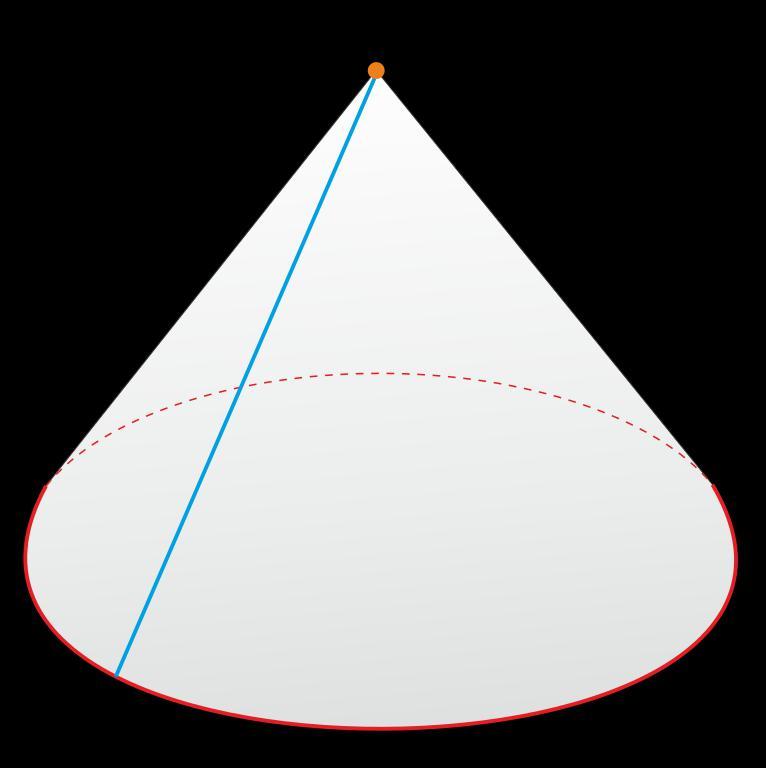
Все эти отрезки являются образующими конуса. Они наклонные к основанию геометрического тела, и в случае прямого конуса их проекции равны, так как вершина равноотдалена от точек круга основания. Таким образом, можно сделать вывод, что в правильном (прямом) конусе образующие равны, то есть имеют одинаковую длину и образуют одинаковые углы с осью (или высотой) и основанием.

Так как в косом (или наклонном) теле вращения вершина смещена по отношению к центру плоскости основания, образующие в таком теле имеют разную длину и проекцию, поскольку каждая из них находится на разном расстоянии от двух любых точек круга основания. Кроме того, углы между ними и высотой конуса также будут отличаться.
Длина образующих в прямом конусе
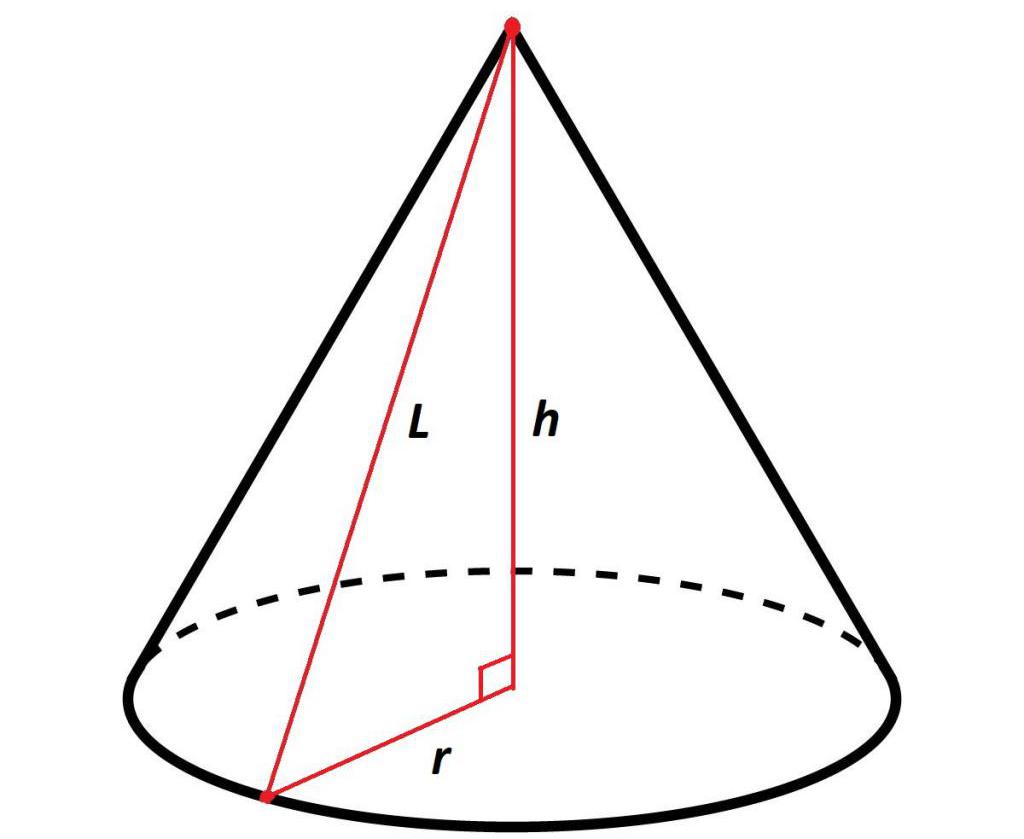
Как написано ранее, высота в прямом геометрическом теле вращения перпендикулярна плоскости основания. Таким образом, образующая, высота и радиус основания создают в конусе прямоугольный треугольник.
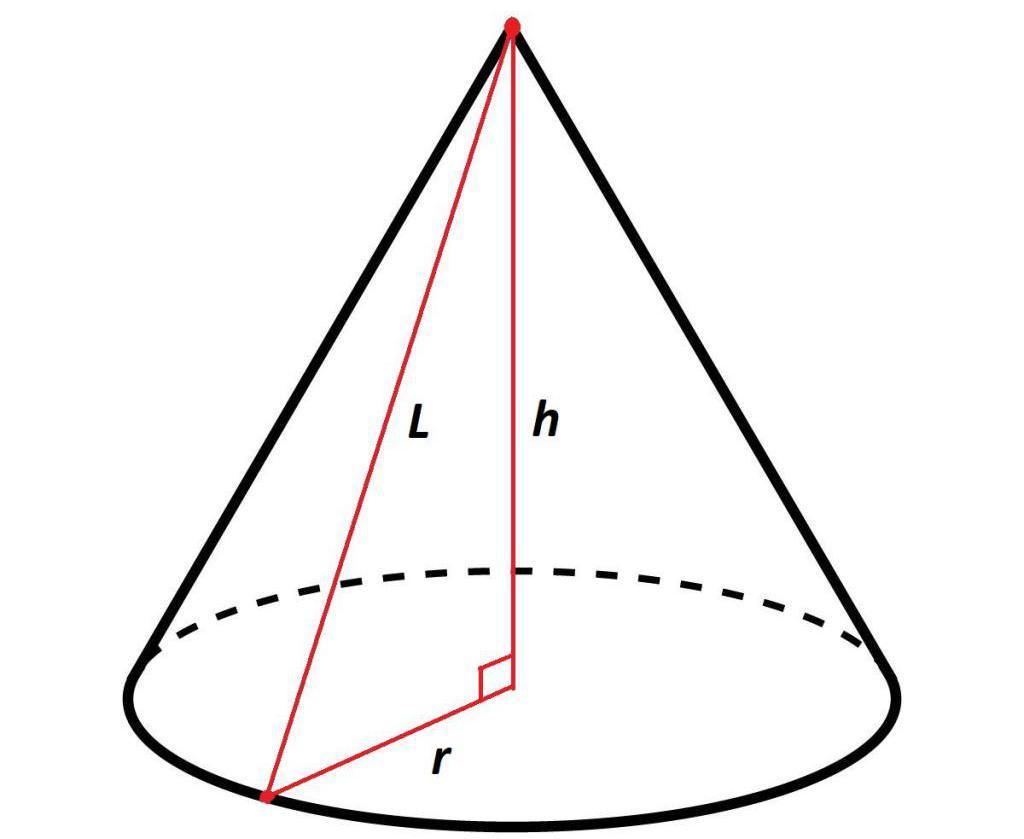
То есть, зная радиус основания и высоту, при помощи формулы из теоремы Пифагора, можно вычислить длину образующей, которая будет равна сумме квадратов радиуса основания и высоты:
l2 = r2+ h2 или l = √r2 + h2
где l – образующая;
r – радиус;
h – высота.
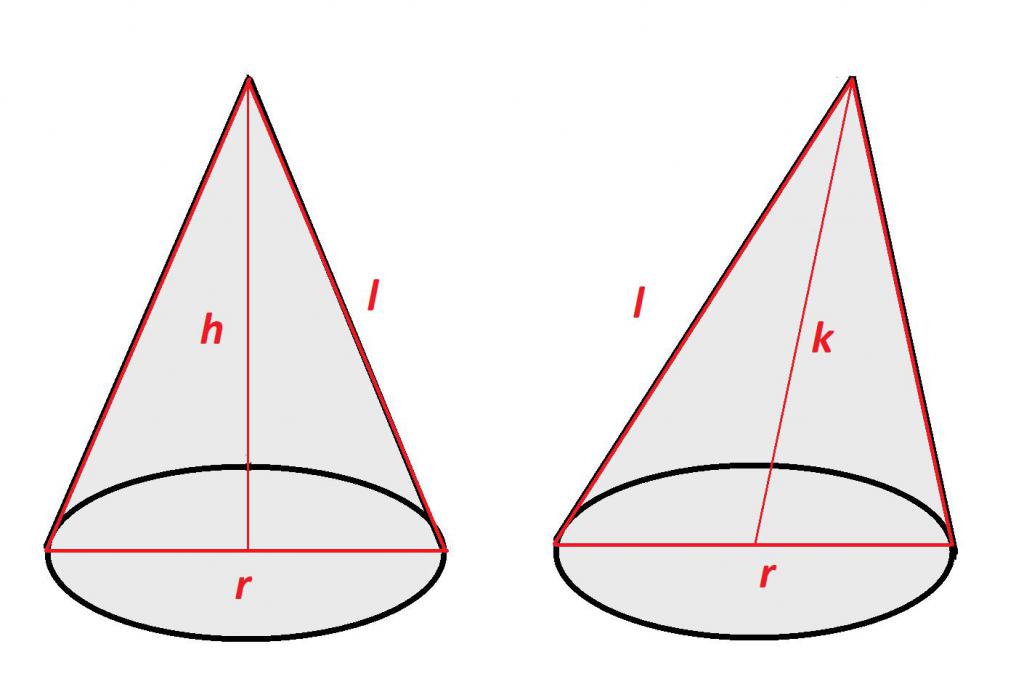
Образующая в наклонном конусе
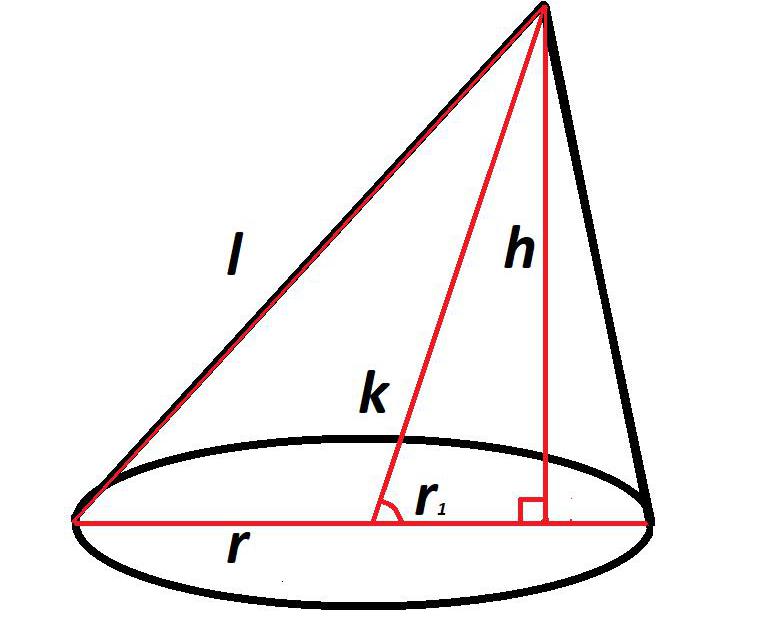
Исходя из того, что в косом, или наклонном конусе образующие имеют не одинаковую длину, рассчитать их без дополнительных построений и вычислений не получится.
Прежде всего необходимо знать высоту, длину оси и радиус основания.
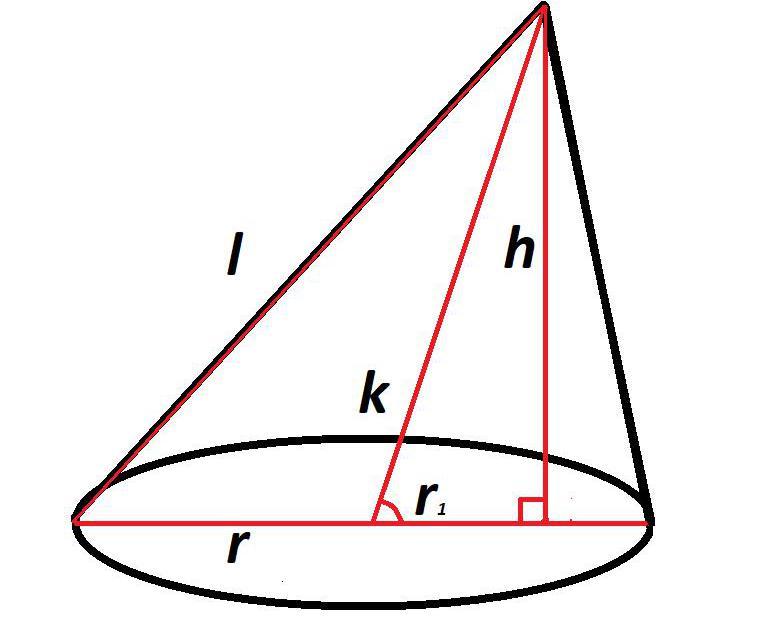
Имея эти данные, можно рассчитать часть радиуса, лежащую между осью и высотой, по формуле из теоремы Пифагора:
r1= √k2 – h2
где r1 – это часть радиуса между осью и высотой;
k – длина оси;
h – высота.
В результате сложения радиуса (r) и его части, лежащей между осью и высотой (r1), можно узнать полную сторону прямоугольного треугольника, сформированного образующей конуса, его высотой и частью диаметра:
R = r + r1
где R – катет треугольника, образованного высотой, образующей и частью диаметра основания;
r – радиус основания;
r1 – часть радиуса между осью и высотой.
Пользуясь все той же формулой из теоремы Пифагора, можно найти длину образующей конуса:
l = √h2+ R2
или, не производя отдельно расчет R, объединить две формулы в одну:
l = √h2 + (r + r1)2.
Несмотря на то, прямой или косой конус и какие вводные данные, все способы нахождения длины образующей всегда сводятся к одному итогу – использованию теоремы Пифагора.
Сечение конуса
Осевым сечением конуса называется плоскость, проходящая по его оси либо высоте. В прямом конусе такое сечение представляет собой равнобедренный треугольник, в котором высотой треугольника является высота тела, его сторонами выступают образующие, а основание – это диаметр основания. В равностороннем геометрическом теле осевое сечение является равносторонним треугольником, так как в этом конусе диаметр основания и образующие равны.
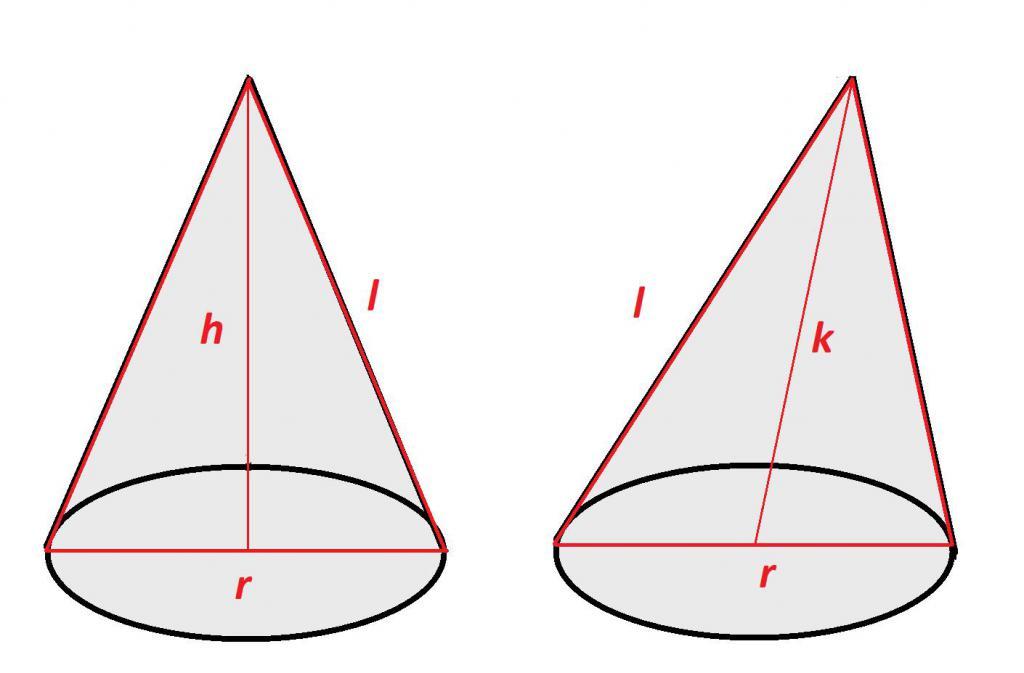
Плоскость осевого сечения в прямом конусе является плоскостью его симметрии. Причиной этому служит то, что его вершина находится над центром его основания, то есть плоскость осевого сечения делит конус на две одинаковые части.
Так как в наклонном объемном теле высота и ось не совпадают, плоскость осевого сечения может не включать в себя высоту. Если осевых сечений в таком конусе можно построить множество, так как для этого необходимо соблюдать лишь одно условие – оно должно проходить только через ось, то осевое сечение плоскости, которому будет принадлежать высота этого конуса, можно провести лишь одно, потому что количество условий увеличивается, а, как известно, две прямые (вместе) могут принадлежать только одной плоскости.
Площадь сечения
Упомянутое ранее осевое сечение конуса представляет собой треугольник. Исходя из этого, его площадь можно рассчитать по формуле площади треугольника:
S = 1/2 * d * h или S = 1/2 * 2r * h
где S – это площадь сечения;
d – диаметр основания;
r – радиус;
h – высота.
В косом, или наклонном конусе сечение по оси также является треугольником, поэтому в нем площадь сечения рассчитывается аналогично.
Объем
Поскольку конус является объемной фигурой в трехмерном пространстве, то можно вычислить его объем. Объемом конуса называется число, которое характеризует это тело в единице измерения объема, то есть в м3. Расчет не зависит от того, прямой он или косой (наклонный), так как формулы для двух этих видов тел не отличаются.
Как указано ранее, образование прямого конуса происходит вследствие вращения прямоугольного треугольника по одному из его катетов. Наклонный же, или косой конус образуется иначе, поскольку его высота смещена в сторону от центра плоскости основания тела. Тем не менее такие отличия в строении не влияют на методику расчета его объема.
Расчет объема
Формула объема любого конуса выглядит следующим образом:
V = 1/3 * π * h * r2
где V – это объем конуса;
h – высота;
r – радиус;
π – константа, равная 3,14.
Для того чтобы рассчитать обьем конуса, необходимо иметь данные о высоте и радиусе основания тела.

Для расчета высоты тела необходимо знать радиус основания и длину его образующей. Поскольку радиус, высота и образующая объединяются в прямоугольный треугольник, то высоту можно рассчитать по формуле из теоремы Пифагора (a2+ b2= c2 или в нашем случае h2+ r2= l2, где l – образующая). Высота при этом будет рассчитываться путем извлечения квадратного корня из разности квадратов гипотенузы и другого катета:
a = √c2- b2
То есть высота конуса будет равна величине, полученной после извлечения квадратного корня из разности квадрата длины образующей и квадрата радиуса основания:
h = √l2 – r2
Рассчитав таким методом высоту и зная радиус его основания, можно вычислить объем конуса. Образующая при этом играет важную роль, так как служит вспомогательным элементом в расчетах.
Аналогичным образом, если известна высота тела и длина его образующей, можно узнать радиус его основания, извлекая квадратный корень из разности квадрата образующей и квадрата высоты:
r = √l2 – h2
После чего по той же формуле, что указана выше, рассчитать объем конуса.
Объем наклонного конуса
Так как формула объема конуса одинакова для всех видов тела вращения, отличие в его расчете составляет поиск высоты.
Для того чтобы узнать высоту наклонного конуса, вводные данные должны включать длину образующей, радиус основания и расстояние между центром основания и местом пересечения высоты тела с плоскостью его основания. Зная это, можно с легкостью рассчитать ту часть диаметра основания, которая будет являться основанием прямоугольного треугольника (образованного высотой, образующей и плоскостью основания). После чего, снова используя теорему Пифагора, произвести расчет высоты конуса, а впоследствии и его объема.
Геометрия является разделом математики, изучающим структуры в пространстве и отношение между ними. В свою очередь она также состоит из разделов, и одним из них является стереометрия. Она предусматривает изучение свойств объемных фигур, находящихся в пространстве: куба, пирамиды, шара, конуса, цилиндра и др.
Конус – это тело в евклидовом пространстве, которое ограничивает коническая поверхность и плоскость, на которой лежат концы ее образующих. Его образование происходит в процессе вращения прямоугольного треугольника вокруг любого из его катетов, поэтому он относится к телам вращения.
Составляющие конуса
Различают следующие виды конусов: косой (или наклонный) и прямой. Косым называется тот, ось которого пересекается с центром его основания не под прямым углом. По этой причине высота в таком конусе не совпадает с осью, так как она является отрезком, который опущен из вершины тела на плоскость его основания под углом 90°.
Тот конус, ось которого расположена перпендикулярно к его основанию, называется прямым. Ось и высота в таком геометрическом теле совпадают по причине того, что вершина в нем расположена над центром диаметра основания.
Конус состоит из следующих элементов:
- Круга, являющегося его основанием.
- Боковой поверхности.
- Точки, не лежащей в плоскости основания, называющейся вершиной конуса.
- Отрезков, которые соединяют точки круга основания геометрического тела и его вершину.
Все эти отрезки являются образующими конуса. Они наклонные к основанию геометрического тела, и в случае прямого конуса их проекции равны, так как вершина равноотдалена от точек круга основания. Таким образом, можно сделать вывод, что в правильном (прямом) конусе образующие равны, то есть имеют одинаковую длину и образуют одинаковые углы с осью (или высотой) и основанием.
Так как в косом (или наклонном) теле вращения вершина смещена по отношению к центру плоскости основания, образующие в таком теле имеют разную длину и проекцию, поскольку каждая из них находится на разном расстоянии от двух любых точек круга основания. Кроме того, углы между ними и высотой конуса также будут отличаться.
Длина образующих в прямом конусе
Как написано ранее, высота в прямом геометрическом теле вращения перпендикулярна плоскости основания. Таким образом, образующая, высота и радиус основания создают в конусе прямоугольный треугольник.
То есть, зная радиус основания и высоту, при помощи формулы из теоремы Пифагора, можно вычислить длину образующей, которая будет равна сумме квадратов радиуса основания и высоты:
l2 = r2+ h2 или l = √r2 + h2
где l – образующая;
r – радиус;
h – высота.
Образующая в наклонном конусе
Исходя из того, что в косом, или наклонном конусе образующие имеют не одинаковую длину, рассчитать их без дополнительных построений и вычислений не получится.
Прежде всего необходимо знать высоту, длину оси и радиус основания.
Имея эти данные, можно рассчитать часть радиуса, лежащую между осью и высотой, по формуле из теоремы Пифагора:
r1= √k2 – h2
где r1 – это часть радиуса между осью и высотой;
k – длина оси;
h – высота.
В результате сложения радиуса (r) и его части, лежащей между осью и высотой (r1), можно узнать полную сторону прямоугольного треугольника, сформированного образующей конуса, его высотой и частью диаметра:
R = r + r1
где R – катет треугольника, образованного высотой, образующей и частью диаметра основания;
r – радиус основания;
r1 – часть радиуса между осью и высотой.
Пользуясь все той же формулой из теоремы Пифагора, можно найти длину образующей конуса:
l = √h2+ R2
или, не производя отдельно расчет R, объединить две формулы в одну:
l = √h2 + (r + r1)2.
Несмотря на то, прямой или косой конус и какие вводные данные, все способы нахождения длины образующей всегда сводятся к одному итогу – использованию теоремы Пифагора.
Сечение конуса
Осевым сечением конуса называется плоскость, проходящая по его оси либо высоте. В прямом конусе такое сечение представляет собой равнобедренный треугольник, в котором высотой треугольника является высота тела, его сторонами выступают образующие, а основание – это диаметр основания. В равностороннем геометрическом теле осевое сечение является равносторонним треугольником, так как в этом конусе диаметр основания и образующие равны.
Плоскость осевого сечения в прямом конусе является плоскостью его симметрии. Причиной этому служит то, что его вершина находится над центром его основания, то есть плоскость осевого сечения делит конус на две одинаковые части.
Так как в наклонном объемном теле высота и ось не совпадают, плоскость осевого сечения может не включать в себя высоту. Если осевых сечений в таком конусе можно построить множество, так как для этого необходимо соблюдать лишь одно условие – оно должно проходить только через ось, то осевое сечение плоскости, которому будет принадлежать высота этого конуса, можно провести лишь одно, потому что количество условий увеличивается, а, как известно, две прямые (вместе) могут принадлежать только одной плоскости.
Площадь сечения
Упомянутое ранее осевое сечение конуса представляет собой треугольник. Исходя из этого, его площадь можно рассчитать по формуле площади треугольника:
S = 1/2 * d * h или S = 1/2 * 2r * h
где S – это площадь сечения;
d – диаметр основания;
r – радиус;
h – высота.
В косом, или наклонном конусе сечение по оси также является треугольником, поэтому в нем площадь сечения рассчитывается аналогично.
Объем
Поскольку конус является объемной фигурой в трехмерном пространстве, то можно вычислить его объем. Объемом конуса называется число, которое характеризует это тело в единице измерения объема, то есть в м3. Расчет не зависит от того, прямой он или косой (наклонный), так как формулы для двух этих видов тел не отличаются.
Как указано ранее, образование прямого конуса происходит вследствие вращения прямоугольного треугольника по одному из его катетов. Наклонный же, или косой конус образуется иначе, поскольку его высота смещена в сторону от центра плоскости основания тела. Тем не менее такие отличия в строении не влияют на методику расчета его объема.
Расчет объема
Формула объема любого конуса выглядит следующим образом:
V = 1/3 * π * h * r2
где V – это объем конуса;
h – высота;
r – радиус;
π – константа, равная 3,14.
Для того чтобы рассчитать обьем конуса, необходимо иметь данные о высоте и радиусе основания тела.
Для расчета высоты тела необходимо знать радиус основания и длину его образующей. Поскольку радиус, высота и образующая объединяются в прямоугольный треугольник, то высоту можно рассчитать по формуле из теоремы Пифагора (a2+ b2= c2 или в нашем случае h2+ r2= l2, где l – образующая). Высота при этом будет рассчитываться путем извлечения квадратного корня из разности квадратов гипотенузы и другого катета:
a = √c2– b2
То есть высота конуса будет равна величине, полученной после извлечения квадратного корня из разности квадрата длины образующей и квадрата радиуса основания:
h = √l2 – r2
Рассчитав таким методом высоту и зная радиус его основания, можно вычислить объем конуса. Образующая при этом играет важную роль, так как служит вспомогательным элементом в расчетах.
Аналогичным образом, если известна высота тела и длина его образующей, можно узнать радиус его основания, извлекая квадратный корень из разности квадрата образующей и квадрата высоты:
r = √l2 – h2
После чего по той же формуле, что указана выше, рассчитать объем конуса.
Объем наклонного конуса
Так как формула объема конуса одинакова для всех видов тела вращения, отличие в его расчете составляет поиск высоты.
Для того чтобы узнать высоту наклонного конуса, вводные данные должны включать длину образующей, радиус основания и расстояние между центром основания и местом пересечения высоты тела с плоскостью его основания. Зная это, можно с легкостью рассчитать ту часть диаметра основания, которая будет являться основанием прямоугольного треугольника (образованного высотой, образующей и плоскостью основания). После чего, снова используя теорему Пифагора, произвести расчет высоты конуса, а впоследствии и его объема.
Поскольку радиус конуса характеризует размер его основания, то зная его, можно найти диаметр, длину окружности и площадь круга, лежащего в основании. Диаметр представляет собой удвоенный радиус, длина окружности – удвоенный радиус, умноженный на число π, а площадь круга – квадрат радиуса, умноженный на число π.
d=2r
P=2πr
S_(осн.)=πr^2
Зная радиус и образующую конуса, можно уже найти его высоту, угол между образующей и основанием, угол раствора конуса. Высота конуса через радиус и образующую ищется по теореме Пифагора в прямоугольном треугольнике, оттуда же можно вычислить и угол β через тригонометрические отношения сторон. Угол α можно найти из равнобедренного треугольника, образованного двумя образующими и диаметром, отняв из 180 градусов два угла β. (рис.40.1, 40.2)
h=√(l^2-r^2 )
cosβ=r/l
α=180°-2β
Площадь боковой поверхности конуса равна произведению полупериметра основания на образующую или произведению числа π на радиус и образующую. Чтобы найти площадь полной поверхности, зная радиус и образующую конуса, необходимо прибавить к площади боковой поверхности произведение числа π на квадрат радиуса, что является площадью основания конуса.
S_(б.п.)=πrl
S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=πr(l+r)
Объем конуса, также как и объем пирамиды рассчитывается как одна треть основания, умноженная на высоту.
V=1/3 S_(осн.) h=(πr^2 h)/3
Радиус сферы, вписанной в конус, вычисляется как произведение высоты на радиус конуса, деленное на сумму радиуса и образующей. Радиус сферы, описанной вокруг конуса, представляет собой отношение квадрата образующей к удвоенной высоте. (рис.40.3, 40.4)
r_1=hr/(l+r)=(r√(l^2-r^2 ))/(l+r)
R=l^2/2h
Площадь круга и его частей. Длина окружности и ее дуг
Основные определения и свойства
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности
Часть окружности, расположенная между двумя точками окружности
Конечная часть плоскости, ограниченная окружностью
Часть круга, ограниченная двумя радиусами
Часть круга, ограниченная хордой
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
| Фигура | Рисунок | Определения и свойства |
| Окружность |  |
|
| Дуга |  |
|
| Круг |  |
|
| Сектор |  |
|
| Сегмент |  |
|
| Правильный многоугольник |  |
|
 |
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности
Дуга
Часть окружности, расположенная между двумя точками окружности
Круг
Конечная часть плоскости, ограниченная окружностью
Сектор
Часть круга, ограниченная двумя радиусами
Сегмент
Часть круга, ограниченная хордой
Правильный многоугольник
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей

где R – радиус круга, D – диаметр круга

если величина угла α выражена в радианах

если величина угла α выражена в градусах

если величина угла α выражена в радианах

если величина угла α выражена в градусах
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |  |
|
| Площадь сектора |  |
|
| Площадь сегмента |
| Площадь круга |
 |

где R – радиус круга, D – диаметр круга
Площадь сектора

если величина угла α выражена в радианах

если величина угла α выражена в градусах
Площадь сегмента

если величина угла α выражена в радианах

если величина угла α выражена в градусах
Формулы для длины окружности и её дуг
где R – радиус круга, D – диаметр круга
если величина угла α выражена в радианах

если величина угла α выражена в градусах
| Длина окружности |
 |
где R – радиус круга, D – диаметр круга
Длина дуги
если величина угла α выражена в радианах

если величина угла α выражена в градусах
Площадь круга
Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .
Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .
Таким образом, площадь круга радиуса R , обозначаемая S , равна
Длина окружности
то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:
откуда вытекает формула для длины окружности радиуса R :
Следствие . Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем
В случае, когда величина α выражена в в радианах, получаем
Длина дуги
На этой странице приведены две формулы для расчета длины дуги окружности — через радиус и угол между ними и по формуле Гюйгенса. Также вы можете рассчитать длину дуги окружности с помощью калькуляторов, которые используют эти формулы.
Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.
Длина окружности
О чем эта статья:
6 класс, 9 класс, ЕГЭ/ОГЭ
Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так – l
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Как найти длину окружности через диаметр
Хорда — это отрезок, который соединяет две точки окружности.
Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:
π— число пи — математическая константа, примерно равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, примерно равное 3,14
r – радиус окружности
Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, примерно равное 3,14
S — площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, примерно равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
π – математическая константа, примерно равная 3,14
a – сторона квадрата
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, примерно равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен Подставим туда наши переменные и получим
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Обучение на курсах по математике поможет закрепить полученные знания на практике.
[spoiler title=”источники:”]
http://mnogoformul.ru/dlina-dugi
http://skysmart.ru/articles/mathematic/dlina-okruzhnosti
[/spoiler]