06
Сен 2019
Категория: 16 (С5) Планиметр. задачиПланиметрияСправочные материалы
Теорема о длине внешней общей касательной к окружностям
2019-09-06
2019-09-08
Данное утверждение может быть очень полезно при решении задач на внешне касающиеся окружности.
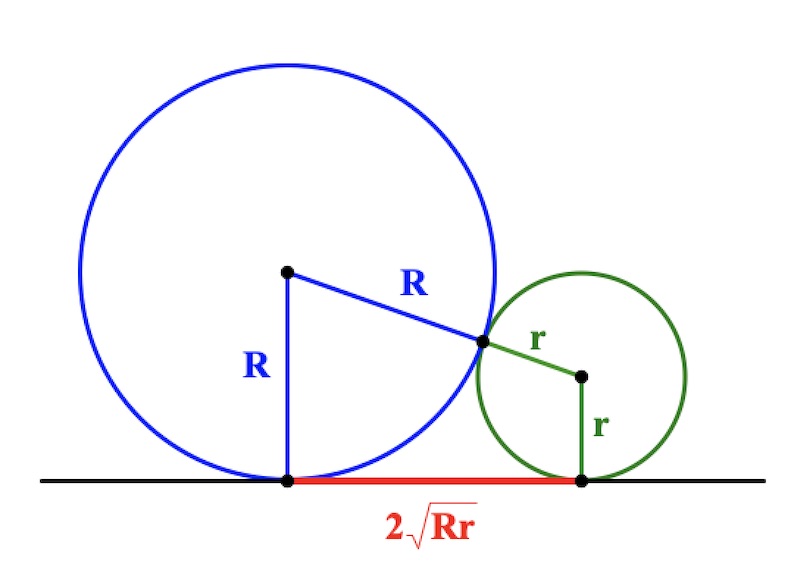
Теорема Если две окружности касаются внешним образом, то длина отрезка общей внешней касательной равна удвоенному среднему пропорциональному их радиусов.
Доказательство смотрите на Youtube канале
Применение теоремы при решении указанной задачи Видео*
О кругах Форда слышали?
Также смотрите применение теоремы при решении задачи
Автор: egeMax |
Нет комментариев
Утверждение
Если две окружности касаются внешне, то длина отрезка общей внешней касательной равна удвоенному среднему пропорциональному их радиусов.
Дано: окр. (O1; R) и окр.(O2; r) касаются внешне в точке D, AB — общая касательная,
окр. (O1; R)∩AB=A, окр.(O2; r)∩AB=B.
Доказать:
![[AB = 2sqrt {Rr} ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-cf2f4d8f376b2053ef7f35661aad2d28_l3.png "Rendered by QuickLaTeX.com")
Доказательство:
Соединим центры окружностей с точками касания.
ABO2O1 — прямоугольная трапеция (по доказанному).
Из точки O2 на сторону AO1 опустим перпендикуляр O2F. Четырёхугольник ABO2F — прямоугольник (так как у него все углы прямые). Поэтому его противоположные стороны равны: FO2=AB, AF=BO2=r.
Рассмотрим прямоугольный треугольник O1O2F.
FO1=AO1-AF=R-r, O1O2=O1D+O2D=R+r.
По теореме Пифагора
![[{O_1}O_2^2 = FO_1^2 + FO_2^2,]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-a4ad956b17fe0defa943421e9d6bb1cf_l3.png "Rendered by QuickLaTeX.com")
![[F{O_2} = sqrt {{O_1}O_2^2 - FO_1^2} ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-86193493aa922364dfb95cc889ad4782_l3.png "Rendered by QuickLaTeX.com")
![[F{O_2} = sqrt {{{(R + r)}^2} - {{(R - r)}^2}} = ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-f5fddf1724f91eaf2955f9d57bca49db_l3.png "Rendered by QuickLaTeX.com")
![[ = sqrt {{R^2} + 2Rr + {r^2} - {R^2} + 2Rr - {r^2}} = 2sqrt {Rr} ,]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-d01ab4343bdb79746a7df104ea202849_l3.png "Rendered by QuickLaTeX.com")
а значит, и
![[AB = 2sqrt {Rr} .]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-a693d008b04ba60271ae2bd2d4e10576_l3.png "Rendered by QuickLaTeX.com")
Что и требовалось доказать.
Угол между касательной и хордой
Угол между касательной и хордой равен половине градусной меры дуги, которая находится внутри угла.
Прежде всего: как это понимать? Подробнее о том, что такое «градусная мера дуги», написано в теме «Окружность. Вписанный угол».
Здесь напомним только, что в дуге столько же градусов, сколько в центральном угле, заключающем эту дугу.
То есть «градусная мера дуги» – это «сколько градусов в центральном угле» – и всё!
Ну вот, как говорит Карлсон, продолжаем разговор. Рисуем ещё раз теорему об угле между касательной и хордой.
Смотри, хорда ( displaystyle AB) разбила окружность на две дуги. Одна дуга находится ВНУТРИ угла ( displaystyle BAC), а другая дуга – внутри угла ( displaystyle BAD).
И теорема об угле между касательной и хордой говорит, что ( displaystyle angle CAB) равен ПОЛОВИНЕ угла ( displaystyle AOB), ( displaystyle angle DAB) равен ПОЛОВИНЕ большего (на рисунке — зеленого) угла ( displaystyle AOB).
При чем же тут тот факт, что радиус, проведенный в точку касания, перпендикулярен касательной?
Сейчас и увидим. ( displaystyle OA) – радиус, ( displaystyle AC) – касательная.
Значит, ( displaystyle angle OAC=90{}^circ ).
Поэтому:( displaystyle angle 1=90{}^circ -angle 4).
Но ( displaystyle angle 2=angle 1) (( displaystyle OA) и ( displaystyle OB) – радиусы)( displaystyle angle 2=90{}^circ -angle 4).
И осталось вспомнить, что сумма углов треугольника ( displaystyle AOB) равна ( displaystyle 180{}^circ ).
Пишем:
Короче:
Здорово, правда? И самым главным оказалось то, что ( displaystyle angle OAC=90{}^circ ).
Равенство отрезков касательных
Задумывался ли ты над вопросом «а сколько касательных можно провести из одной точки к одной окружности»? Вот, представь себе, ровно две! Вот так:
А ещё более удивительный факт состоит в том, что:
Отрезки касательных, проведённых из одной точки к одной окружности, равны.
То есть, на нашем рисунке, ( displaystyle AB=AC).
И для этого факта тоже самым главным является то, что радиус, проведённый в точку касания, перпендикулярен касательной.
Вот, убедись.
Проведём радиусы ( displaystyle OB) и ( displaystyle OC) и соединим ( displaystyle O) и ( displaystyle A).
( displaystyle OB) – радиус.
( displaystyle AB) – касательная, значит, ( displaystyle OBbot AB).
Ну, и так же ( displaystyle OCbot AC).
Получилось два прямоугольных треугольника ( displaystyle AOB) и ( displaystyle AOC), у которых:
- ( displaystyle OB=OC) — равные катеты
- ( displaystyle OA) — общая гипотенуза
( displaystyle Rightarrow Delta AOB = Delta AOC)
(заглядываем в тему «Прямоугольный треугольник«, если не помним, когда бывают равны прямоугольные треугольники).
Но раз ( displaystyle Delta AOB=Delta AOC,) то( displaystyle AB=AC). УРА!
И ещё раз повторим – этот факт тоже очень важный:
Отрезки касательных, проведённых из одной точки, – равны.
И есть ещё один факт, который мы здесь не будем доказывать, но он может оказаться тебе полезен при решении задач.
Для любой прямой ( displaystyle AD), пересекающей окружность,( displaystyle ADcdot AC=A{{B}^{2}}), где ( displaystyle AB) – отрезок касательной.
Хитроумными словами об этом говорят так:
«Квадрат длины отрезка касательной равен произведению секущей на её внешнюю часть».
Страшно? Не бойся, помни только, что в буквах это:
Построение общей внешней касательной к двум окружностям
Построение общей внешней касательной к двум окружностям. Даны две окружности (а это значит, что даны также и их центры O1 и O2). И требуется построить к ним общую внешнюю касательную, то есть такую касательную, что данные окружности лежат от неё по одну сторону. Радиус большей окружности — называем R, радиус меньшей окружности — r. И сначала внутри большей окружности построим вспомогательную окружность вокруг того же центра и радиуса (R-r). Затем построим из центра меньшей окружности вспомогательную касательную к вспомогательной окружности, и требуемая внешняя касательная будет параллельна вспомогательной касательной.
Отложим первый вспомогательный луч с началом в точке A. Замерим циркулем радиус большей окружности, и тем же раствором циркуля от начала первого луча отложим отрезок AB равный R. Теперь циркулем замерим радиус меньшей окружности, и тем же раствором циркуля от точки B отложим отрезок BC, равный r. Получился AC = R — r. Замерим AC циркулем, и тем же раствором циркуля построим первую вспомогательную окружность с центром в O1.
Теперь соединим отрезком центры O1 и O2. Произвольным раствором циркуля строим вторую вспомогательную дугу окружности с центром O1. И тем же раствором циркуля строим третью вспомогательную дугу окружности с центром O2 — так, чтобы третья дуга пересекала вторую в двух точках (называем их D и E). Соединяем D и E отрезком, который пересекает O1O2 в середине — эту точку называем F. Теперь замерим циркулем FO1 и этим раствором циркуля строим четвёртую вспомогательную окружность с центром в F на отрезке O1O2, как на диаметре. Эта четвёртая окружность пересекает первую вспомогательную окружность в двух точках (называем их G и H). Выбираем из этих двух точек ту, которая нам больше нравится (мне нравится точка H), и соединяем прямой с точкой O2. Прямая HO2 — это касательная к первой вспомогательной окружности, проходящая через центр маленькой данной окружности.
Прямая HO2 пересекла меньшую окружность в двух точках (называем их K и L). Эти точки равноотстоят от O2 и помогут нам построить перпендикуляр к HO2. Произвольным раствором циркуля проводим пятую вспомогательную дугу окружности с центром в K. Тем же раствором циркуля проводим шестую вспомогательную дугу окружности с центром в L — так, чтоб шестая дуга пересекала пятую в некоторой точке (называем точку M). Соединяем O2 и M прямой — эта прямая (перпендикуляр к HO2) пересекает меньшую данную окружность в некоторой точке (называем её N).
Теперь через N проведём прямую, параллельную вспомогательной касательной HO2. Произвольным раствором циркуля строим седьмую вспомогательную окружность с центром в точке N — так, чтоб седьмая окружность пересекала HO2 в двух точках (точки называем P и Q). Тем же раствором циркуля строим восьмую вспомогательную окружность с центром в P, и восьмая окружность пересекает вспомогательную касательную HO2 в двух точках (точки называем Z и S). Тем же раствором циркуля проводим девятую вспомогательную дугу окружности с центром в Z — так, чтобы девятая дуга пересекала седьмую окружность в некоторой точке (точку называем T). Соединяем N и Т прямой — эта прямая NT и будет требуемой общей внешней касательной к двум данным окружностям.
И вот почему: NT проходит через конец радиуса O2N, лежащий на окружности. Также по построению NT параллельна HO2 и перпендикулярна радиусу O2N — следовательно, NT — касательная к малой данной окружности. Теперь проведём радиус O1H и продлим его до пересечения с прямой TN (точку пересечения называем U). Радиус O1H перпендикулярен касательной O2H — значит, угол O2HU — прямой. Получилось, что в четырёхугольнике UHO2N есть три прямых угла — значит и четвёртый угол HUN прямой, и UHO2N — прямоугольник, в котором сторона HU равна противоположной стороне O2N, то есть радиусу r. Теперь можем найти длину отрезка O1U (состоящего из O1H и HU). Длина равна сумме длин O1H и HU, то есть (R — r) + r = R. Выходит, что U отстоит от O1 на R, то есть U лежит на большой данной окружности, а это значит, что TN, проходящая через U — проходит через конец радиуса O1U, лежащий на окружности, и перпендикулярна радиусу, то есть TN — касательная к большой данной окружности. Построение закончено.
Найдите длину отрезка общей касательной к двум окружностям, заключенного между точками касания, если радиусы окружностей равны 31 и 17, а расстояние между центрами окружностей равно 50.
Спрятать решение
Решение.
Пусть центры окружностей — точки O1 и O2, а A и B — точки касания. Проведем через точку B прямую, параллельную O1O2. Точку пересечения этой прямой с O1A обозначим K. Треугольник KAB — прямоугольный.
Возможны два случая расположения окружностей и общей касательной.
Случай 1. Окружности лежат по одну сторону от касательной.
Случай 2. Окружности лежат по разные стороны от касательной.
Обозначим радиусы окружностей R и r, расстояние между центрами окружностей l. В первом случае AK = R − r, во втором случае AK = R + r. Из прямоугольного треугольника KAB находим:
в первом случае
во втором случае
Ответ: 48 или 14.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Рассмотрены все возможные геометрические конфигурации, и получен правильный ответ | 3 |
| Рассмотрена хотя бы одна возможная конфигурация, в которой получено правильное значение искомой величины | 2 |
| Рассмотрена хотя бы одна возможная геометрическая конфигурация, в которой получено значение искомой величины, неправильное из-за геометрической ошибки | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
