Как посчитать длину окружности
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать длину окружности
Чтобы посчитать длину окружности (круга) просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Для того чтобы определить длину окружности вам необходимо знать её радиус или диаметр, либо её площадь. Зная хотя бы один из этих параметров, введите его в соответствующие поле и получите результат в виде длины окружности (длины дуги в 360 градусов).
Как посчитать длину окружности зная диаметр
Какая длина у окружности если
её диаметр ?
Ответ:
0
Какова длина окружности (С) если её диаметр d?
Формула
С = π⋅d, где π ≈ 3.14
Пример
Если диаметр круга равен 1 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная радиус
Какая длина у окружности если
её радиус ?
Ответ:
0
Какова длина окружности (С) если её радиус r?
Формула
С = 2⋅π⋅r, где π ≈ 3.14
Пример
Если радиус круга равен 0.5 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная её площадь
Какая длина у окружности если
её площадь ?
Ответ:
0
Какова длина окружности (С) если её площадь S?
Формула
С = 2π⋅√S/π, где π ≈ 3.14
Пример
Если площадь круга равна 6 см2, то его длина примерно равна 8.68 см.
См. также
8 способов найти длину окружности
Выбирайте формулу, ориентируясь на известные величины.
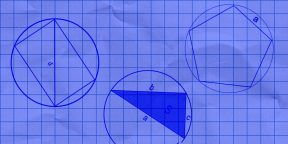
1. Как найти длину окружности через диаметр
Просто умножьте диаметр на число пи.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- d —диаметр окружности.
2. Как найти длину окружности через радиус
Умножьте число пи на два радиуса.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- r — радиус окружности.
3. Как вычислить длину окружности через площадь круга
Умножьте число пи на четыре площади круга.
Найдите корень из результата.
- O — искомая длина окружности.
- S – площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
4. Как найти длину окружности через диагональ вписанного прямоугольника
Умножьте число пи на диагональ.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- d – любая диагональ прямоугольника.
5. Как вычислить длину окружности через сторону описанного квадрата
Умножьте число пи на сторону квадрата.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- a – любая сторона квадрата.
6. Как найти длину окружности через стороны и площадь вписанного треугольника
Перемножьте стороны треугольника.
Поделите результат на площадь и на два.
Умножьте полученное число на пи.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- S – площадь треугольника.
- a, b, c – стороны треугольника.
7. Как найти длину окружности через площадь и полупериметр описанного треугольника
Поделите площадь треугольника на его полупериметр.
Умножьте результат на число пи и на два.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- S – площадь треугольника.
- p – полупериметр треугольника (равен половине от суммы всех сторон).
8. Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разделите 180 градусов на количество сторон многоугольника.
Найдите синус полученного числа.
Разделите сторону многоугольника на результат.
Умножьте получившееся число на пи.
- O — искомая длина окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- π (пи) — константа, равная 3,14.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✏️🎓
- Как найти периметр прямоугольника
- 8 способов найти периметр треугольника
- 7 способов найти площадь прямоугольника
- Как перевести обычную дробь в десятичную
- Как освоить устный счёт школьникам и взрослым
Длина (периметр) окружности калькулятор онлайн умеет вычислять длину восемью способами:
- По радиусу.
- По диаметру.
- По площади окружности.
- По диагонали вписанного прямоугольника.
- По стороне описанного квадрата.
- По сторонам и площади описанного треугольника.
- По площади вписанного треугольника.
- По стороне вписанного многогранника.
Сделав расчет периметра на этом онлайн калькуляторе Вы получите не только ответ, но и детальное, пошаговое решение с выводом формул и промежуточных действий.
Длина окружности или периметр окружности – это длина кривой из множества точек которая ограничивает собой круг.
Длина окружности может быть найдена по длине пути, который проедет круг сделав один полный оборот.
Как найти длину окружности?
Найти длину окружности очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
1) По радиусу
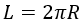
где R – радиус окружности.
2) По диаметру
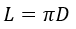
где D – диаметр окружности.
3) По площади окружности
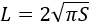
ггде S – площадь окружности.
4) По диагонали вписанного прямоугольника
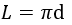
где d – диагональ вписанного прямоугольника.
5) По стороне описанного квадрата
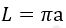
где a – сторона описанного квадрата.
6) По сторонам и площади описанного треугольника
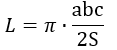
где a,b,c – стороны описанного треугольника, S – его площадь.
7) По площади вписанного треугольника
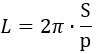
где p – полупериметр вписанного треугольника, S – его площадь.
8) По стороне вписанного многогранника
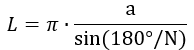
где a – сторона вписанного многогранника, N – количество сторон.
Скачать все формулы в формате Word
Как рассчитать периметр круга или длину окружности
На данной странице калькулятор поможет рассчитать периметр круга или длину окружности онлайн. Для расчета задайте радиус или диаметр.
Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
Через радиус
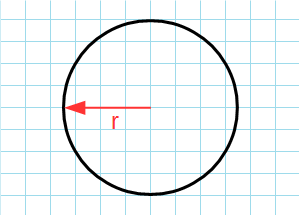
Формула для нахождения длины окружности или периметр круга через радиус:
π – константа равная (3.14); r – радиус круга.
Через диаметр
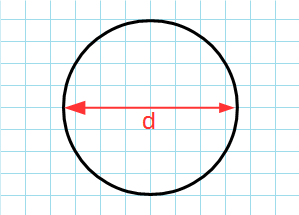
Формула для нахождения длины окружности или периметр круга через диаметр:
π – константа равная (3.14); d – диаметр.
Окружность представляет собой замкнутую кривую, все точки которой находятся на одинаковом расстоянии
от центра. Центр окружности – это точка, которая находится на равном расстоянии от всех точек,
расположенных на одной прямой. Также стоит различать два понятия: окружность и круг. Круг – это
просто часть некого пространства, которое ограничено окружностью. А окружностью представляет собой
совокупность точек на одной прямой. Понятия связаны, но имеют существенные различия.
- Длина окружности через радиус
- Длина окружности через диаметр
- Длина окружности через площадь круга
Через радиус
Для начала стоит сказать, что R- радиус окружности, Р – длина (периметр) окружности. Одним из самых
простых способов для ее вычисления является следующий:
Р = 2R * π
где R — Радиус.
Цифр после
запятой:
Результат в:
Пример. Дана окружность. Учащемуся требуется найти длину окружности, когда у него
есть только радиус. Радиус равен 15 см, тогда длина окружности? Решение. Находим неизвестную
величину по вышеупомянутой формуле: Р = 2R * π, восполняя данные, которые были указаны в условии. К
слову, π — это постоянная математическая величина. Чаще всего в ответах к заданиям она и
остается в таком виде, хотя у нее есть числовое значение, которое равно 3,14. Р = 2 * 15 * 3,14 = 9 см.
см. Решение не вызывает никаких вопросов, так как для нахождения неизвестной требуется только радиус
окружности.
Через диаметр
Диаметр – это радиус, который увеличили в два раза. Он тоже проходит через центр окружности и
касается контура, только уже в двух местах. Но через диаметр можно найти переменную – длину
(периметр) окружности. Это действие выполнимо благодаря следующей формуле:
P = D * π
где D – это диаметр окружности.
Цифр после
запятой:
Результат в:
Пример. Учащемуся необходимо найти длину (периметр) окружности. Из известных данных
только диаметр (D), который равен 20 см. Решение. Используем формулу, которая была указана выше и
подставим известные данные: Р = 20 * 3,14 = 6 см.
Через площадь окружности
Есть еще один способ, который поможет найти длину окружности. Этот способ основан на площади
окружности. Стоит упомянуть, что площадь можно найти по следующей формуле: S= πR², где S – это
площадь окружности, а R – радиус окружности. А длину окружности находят следующим образом:
P = √(S * 4π)
где S — это площадь окружности.
Цифр после
запятой:
Результат в:
Пример. Дана окружность, а учащемуся требуется найти ее длину (периметр). Он имеет
следующие данные: R = 3 см. Тогда чему равна длина окружности. Решение. Сначала требуется найти
площадь вышеуказанной фигуры: S = πR² = 3,14 * 9 = 28,26 см. Далее можно
уже находить и длину окружности, подставляя все уже известные данные в формулу, которая была
упомянута выше: P = √(S * 4π) = √(28,26 * 4 * 3,14) = 1,9 см.
Каждая окружность обладает некоторыми переменными, которые можно и нужно уметь различать. Например,
радиус – это расстояние от центра окружности до любой точки, которая лежит на окружности. Диаметр –
это то понятие, которое связано с радиусом. Он представляет собой отрезок, который проходит через
центр окружности и соединяет точки на этой же окружности, которые лежат напротив друг друга. Диаметр
– это увеличенный вдвое радиус. Любая фигура имеет площадь. Окружность не является
исключением. Таким образом, окружность является довольно важной фигурой, которая имеет множество
составляющих, которые позволяют находить ее длину несколькими способами.
