Длина окружности

О чем эта статья:
6 класс, 9 класс, ЕГЭ/ОГЭ
Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так – l
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Как найти длину окружности через диаметр
Хорда — это отрезок, который соединяет две точки окружности.
Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:
π— число пи — математическая константа, примерно равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, примерно равное 3,14
r – радиус окружности
Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, примерно равное 3,14
S — площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, примерно равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
π – математическая константа, примерно равная 3,14
a – сторона квадрата
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, примерно равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен Подставим туда наши переменные и получим
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Обучение на курсах по математике поможет закрепить полученные знания на практике.
Как посчитать длину окружности
Онлайн калькулятор
Как посчитать длину окружности зная диаметр
Какая длина у окружности если
Какова длина окружности (С) если её диаметр d?
Формула
С = π⋅d , где π ≈ 3.14
Пример
Если диаметр круга равен 1 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная радиус
Какая длина у окружности если
Какова длина окружности (С) если её радиус r?
Формула
С = 2⋅π⋅r , где π ≈ 3.14
Пример
Если радиус круга равен 0.5 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная её площадь
Какая длина у окружности если
Какова длина окружности (С) если её площадь S?
Формула
С = 2π⋅ √ S /π , где π ≈ 3.14
Пример
Если площадь круга равна 6 см 2 , то его длина примерно равна 8.68 см.
Длина окружности через стороны треугольника
Длина окружности

О чем эта статья:
6 класс, 9 класс, ЕГЭ/ОГЭ
Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так — l
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Как найти длину окружности через диаметр
Хорда — это отрезок, который соединяет две точки окружности.
Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:
π— число пи — математическая константа, примерно равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, примерно равное 3,14
r — радиус окружности
Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, примерно равное 3,14
S — площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, примерно равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
π — математическая константа, примерно равная 3,14
a — сторона квадрата
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, примерно равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен Подставим туда наши переменные и получим
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Обучение на курсах по математике поможет закрепить полученные знания на практике.
Треугольник вписанный в окружность

Определение
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.

Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:
Радиус вписанной окружности в треугольник,
если известны площадь и периметр:
Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:
Радиус описанной окружности около треугольника,
если известны все стороны и площадь:
Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:
Площадь треугольника
S — площадь треугольника.
- Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:
Площадь треугольника вписанного в окружность,
если известен полупериметр:
Площадь треугольника вписанного в окружность,
если известен высота и основание:
Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:
Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:
[ S = frac ab cdot sin angle C ]
Периметр треугольника
P — периметр треугольника.
- Периметр треугольника вписанного в окружность,
если известны все стороны:
Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:
Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:
Сторона треугольника
a — сторона треугольника.
- Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:
Сторона треугольника вписанного в
окружность, если известна сторона и два угла:
Средняя линия треугольника
l — средняя линия треугольника.
- Средняя линия треугольника вписанного
в окружность, если известно основание:
Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:
Высота треугольника
h — высота треугольника.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:
Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:
[ h = b cdot sin alpha ]
Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:
Свойства
- Центр вписанной в треугольник окружности
находится на пересечении биссектрис. - В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну. - Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора. - Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров. - Все вершины треугольника, вписанного
в окружность, лежат на окружности. - Сумма всех углов треугольника — 180 градусов.
- Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.
Доказательство
Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.
окружность описана
около треугольника.
- Проведем серединные
перпендикуляры — HO, FO, EO. - O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника. - Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.
окружность описана около треугольника,
что и требовалось доказать.
Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.
Таблица Брадиса — ДЛИНА ОКРУЖНОСТИ ДИАМЕТРА D
Если возникают неполадки в водопроводе, канализации или газовой коммуникации, то приходится заменять и устанавливать новый фрагмент трубопровода. Для реализации операции в домашних условиях учатся находить диаметр труб, вооружившись подручными средствами. Выбирают конкретный метод обмера, опираясь на габариты изделий и расположение трубопровода.

Диаметр трубы можно узнать самостоятельно, нужно знать всего лишь несколько простых способов
- Как в домашних условиях определить овальность трубы большого диаметра
- Правильное измерение диаметра трубы в 3 этапа
- Обмер крупного изделия рулеткой, линейкой, штангенциркулем и без него
- Проверка диаметра труб и остальных параметров в условиях производства: наружный, внутренний показатель
Как найти длину окружности через стороны и площадь вписанного треугольника
Перемножьте стороны треугольника.
Поделите результат на площадь и на два.
Умножьте полученное число на пи.

Иллюстрация: Лайфхакер
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- S – площадь треугольника.
- a, b, c – стороны треугольника.
Расчет объема воды, находящейся во всей системе
Для определения такого параметра, необходимо в формулу подставить значение внутреннего радиуса. Однако сразу появляется проблема. А как рассчитать полный объем воды в трубе всей отопительной системы, в которую входят:
- Радиаторы;
- Расширительный бачок;
- Котел отопления.
Сначала рассчитывается объём радиатора. Для этого открывается его технический паспорт и выписывается значения объема одной секции. Этот параметр умножается на число секций в конкретной батарее. Например, одна равен 1,5 литрам.
Когда установлен биметаллический радиатор, это значение намного меньше. Количество воды в котле можно узнать из паспорта устройства.
Для определения объема расширительного бака, его заполняют измеренным заранее, количеством жидкости.
Очень просто определяется объём труб. Имеющиеся данные для одного метра, определенного диаметра, нужно просто умножить на длину всего трубопровода.
Заметим что в глобальной сети и справочной литературе, можно увидеть специальные таблицы. Они показывают ориентировочные данные изделия. Погрешность приведенных данных достаточно мала, поэтому приведенные в таблице значения, можно смело использовать для вычисления объема воды.
Надо сказать, что при расчете значений, нужно учитывать некоторые характерные отличия. Металлические трубы, имеющие большой диаметр, пропускают количество воды, значительно меньше, чем такие же полипропиленовые трубы.
Причина кроется в гладкости поверхности труб. У стальных изделий она выполнена с большой шероховатостью. ППР трубы не имеют шероховатости на внутренних стенках. Однако при этом стальные изделия имеют больший объем воды, чем в других трубах, одинакового сечения. Поэтому чтобы убедиться, что расчет объема воды в трубах произведен верно, нужно несколько раз перепроверить все данные и подкрепить результат онлайн-калькулятором.
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разделите 180 градусов на количество сторон многоугольника.
Найдите синус полученного числа.
Разделите сторону многоугольника на результат.
Умножьте получившееся число на пи.

Иллюстрация: Лайфхакер
- O — искомая длина окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- π (пи) — константа, равная 3,14.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Таблица. Длина окружности диаметра D.
Таблица. Длина окружности диаметра D. Пример: длина окружности диаметра 1,523 = 4475+9= 4,784
Таблица. Длина окружности диаметра D.
| D | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 1 | 2 | 3 | 4 | 5 |
| 1,0 | 3,142 | 3,173 | 3,204 | 3,236 | 3,267 | 3,299 | 3,330 | 3,362 | 3,393 | 3,424 | 3 | 6 | 9 | 13 | 16 |
| 1,1 | 3,456 | 3,487 | 3,519 | 3,550 | 3,581 | 3,613 | 3,644 | 3,676 | 3,707 | 3,738 | 3 | 6 | 9 | 13 | 16 |
| 1,2 | 3,770 | 3,801 | 3,833 | 3,864 | 3,896 | 3,927 | 3,958 | 3,990 | 4,021 | 4,053 | 3 | 6 | 9 | 13 | 16 |
| 1,3 | 4,084 | 4,115 | 4,147 | 4,178 | 4,210 | 4,241 | 4,273 | 4,304 | 4,335 | 4,367 | 3 | 6 | 9 | 13 | 16 |
| 1,4 | 4,398 | 4,430 | 4,461 | 4,492 | 4,524 | 4,555 | 4,587 | 4,618 | 4,650 | 4,681 | 3 | 6 | 9 | 13 | 16 |
| 1,5 | 4,712 | 4,744 | 4,775 | 4,807 | 4,838 | 4,869 | 4,901 | 4,932 | 4,964 | 4,995 | 3 | 6 | 9 | 13 | 16 |
| 1,6 | 5,027 | 5,058 | 5,089 | 5,121 | 5,152 | 5,184 | 5,215 | 5,246 | 5,278 | 5,309 | 3 | 6 | 9 | 13 | 16 |
| 1,7 | 5,341 | 5,372 | 5,404 | 5,435 | 5,466 | 5,498 | 5,529 | 5,561 | 5,592 | 5,623 | 3 | 6 | 9 | 13 | 16 |
| 1,8 | 5,655 | 5,686 | 5,718 | 5,749 | 5,781 | 5,812 | 5,843 | 5,875 | 5,906 | 5,938 | 3 | 6 | 9 | 13 | 16 |
| 1,9 | 5,969 | 6,000 | 6,032 | 6,063 | 6,095 | 6,126 | 6,158 | 6,189 | 6,220 | 6,252 | 3 | 6 | 9 | 13 | 16 |
| 2,0 | 6,283 | 6,315 | 6,346 | 6,377 | 6,409 | 6,440 | 6,472 | 6,503 | 6,535 | 6,566 | 3 | 6 | 9 | 13 | 16 |
| 2,1 | 6,597 | 6,629 | 6,660 | 6,692 | 6,723 | 6,754 | 6,786 | 6,817 | 6,849 | 6,880 | 3 | 6 | 9 | 13 | 16 |
| 2,2 | 6,912 | 6,943 | 6,974 | 7,006 | 7,037 | 7,069 | 7,100 | 7,131 | 7,163 | 7,194 | 3 | 6 | 9 | 13 | 16 |
| 2,3 | 7,226 | 7,257 | 7,288 | 7,320 | 7,351 | 7,383 | 7,414 | 7,446 | 7,477 | 7,508 | 3 | 6 | 9 | 13 | 16 |
| 2,4 | 7,540 | 7,571 | 7,603 | 7,634 | 7,665 | 7,697 | 7,728 | 7,760 | 7,791 | 7,823 | 3 | 6 | 9 | 13 | 16 |
| 2,5 | 7,854 | 7,885 | 7,917 | 7,948 | 7,980 | 8,011 | 8,042 | 8,074 | 8,105 | 8,137 | 3 | 6 | 9 | 13 | 16 |
| 2,6 | 8,168 | 8,200 | 8,231 | 8,262 | 8,294 | 8,325 | 8,357 | 8,388 | 8,419 | 8,451 | 3 | 6 | 9 | 13 | 16 |
| 2,7 | 8,482 | 8,514 | 8,545 | 8,577 | 8,608 | 8,639 | 8,671 | 8,702 | 8,734 | 8,765 | 3 | 6 | 9 | 13 | 16 |
| 2,8 | 8,796 | 8,828 | 8,859 | 8,891 | 8,922 | 8,954 | 8,985 | 9,016 | 9,048 | 9,079 | 3 | 6 | 9 | 13 | 16 |
| 2,9 | 9,111 | 9,142 | 9,173 | 9,205 | 9,236 | 9,268 | 9,299 | 9,331 | 9,362 | 9,393 | 3 | 6 | 9 | 13 | 16 |
| 3,0 | 9,425 | 9,456 | 9,488 | 9,519 | 9,550 | 9,582 | 9,613 | 9,645 | 9,676 | 9,708 | 3 | 6 | 9 | 13 | 16 |
| 3,1 | 9,739 | 9,770 | 9,802 | 9,833 | 9,865 | 9,896 | 9,927 | 9,959 | 9,990 | 10,022 | 3 | 6 | 9 | 13 | 16 |
| 3,2 | 10,053 | 10,085 | 10,116 | 10,147 | 10,179 | 10,210 | 10,242 | 10,273 | 10,304 | 10,336 | 3 | 6 | 9 | 13 | 16 |
| 3,3 | 10,367 | 10,399 | 10,430 | 10,462 | 10,493 | 10,524 | 10,556 | 10,587 | 10,619 | 10,650 | 3 | 6 | 9 | 13 | 16 |
| 3,4 | 10,681 | 10,713 | 10,744 | 10,776 | 10,807 | 10,838 | 10,870 | 10,901 | 10,933 | 10,964 | 3 | 6 | 9 | 13 | 16 |
| 3,5 | 10,996 | 11,027 | 11,058 | 11,090 | 11,121 | 11,153 | 11,184 | 11,215 | 11,247 | 11,278 | 3 | 6 | 9 | 13 | 16 |
| 3,6 | 11,310 | 11,341 | 11,373 | 11,404 | 11,435 | 11,467 | 11,498 | 11,530 | 11,561 | 11,592 | 3 | 6 | 9 | 13 | 16 |
| 3,7 | 11,624 | 11,655 | 11,687 | 11,718 | 11,750 | 11,781 | 11,812 | 11,844 | 11,875 | 11,907 | 3 | 6 | 9 | 13 | 16 |
| 3,8 | 11,938 | 11,969 | 12,001 | 12,032 | 12,064 | 12,095 | 12,127 | 12,158 | 12,189 | 12,221 | 3 | 6 | 9 | 13 | 16 |
| 3,9 | 12,252 | 12,284 | 12,315 | 12,346 | 12,378 | 12,409 | 12,441 | 12,472 | 12,504 | 12,535 | 3 | 6 | 9 | 13 | 16 |
| 4,0 | 12,566 | 12,598 | 12,629 | 12,661 | 12,692 | 12,723 | 12,755 | 12,786 | 12,818 | 12,849 | 3 | 6 | 9 | 13 | 16 |
| 4,1 | 12,881 | 12,912 | 12,943 | 12,975 | 13,006 | 13,038 | 13,069 | 13,100 | 13,132 | 13,163 | 3 | 6 | 9 | 13 | 16 |
| 4,2 | 13,195 | 13,226 | 13,258 | 13,289 | 13,320 | 13,352 | 13,383 | 13,415 | 13,446 | 13,477 | 3 | 6 | 9 | 13 | 16 |
| 4,3 | 13,509 | 13,540 | 13,572 | 13,603 | 13,635 | 13,666 | 13,697 | 13,729 | 13,760 | 13,792 | 3 | 6 | 9 | 13 | 16 |
| 4,4 | 13,823 | 13,854 | 13,886 | 13,917 | 13,949 | 13,980 | 14,012 | 14,043 | 14,074 | 14,106 | 3 | 6 | 9 | 13 | 16 |
| 4,5 | 14,137 | 14,169 | 14,200 | 14,231 | 14,263 | 14,294 | 14,326 | 14,357 | 14,388 | 14,420 | 3 | 6 | 9 | 13 | 16 |
| 4,6 | 14,451 | 14,483 | 14,514 | 14,546 | 14,577 | 14,608 | 14,640 | 14,671 | 14,703 | 14,734 | 3 | 6 | 9 | 13 | 16 |
| 4,7 | 14,765 | 14,797 | 14,828 | 14,860 | 14,891 | 14,923 | 14,954 | 14,985 | 15,017 | 15,048 | 3 | 6 | 9 | 13 | 16 |
| 4,8 | 15,080 | 15,111 | 15,142 | 15,174 | 15,205 | 15,237 | 15,268 | 15,300 | 15,331 | 15,362 | 3 | 6 | 9 | 13 | 16 |
| 4,9 | 15,394 | 15,425 | 15,457 | 15,488 | 15,519 | 15,551 | 15,582 | 15,614 | 15,645 | 15,677 | 3 | 6 | 9 | 13 | 16 |
| 5,0 | 15,708 | 15,739 | 15,771 | 15,802 | 15,834 | 15,865 | 15,896 | 15,928 | 15,959 | 15,991 | 3 | 6 | 9 | 13 | 16 |
| 5,1 | 16,022 | 16,054 | 16,085 | 16,116 | 16,148 | 16,179 | 16,211 | 16,243 | 16,273 | 16,305 | 3 | 6 | 9 | 13 | 16 |
| 5,2 | 16,336 | 16,368 | 16,399 | 16,431 | 16,462 | 16,493 | 16,525 | 16,556 | 16,588 | 16,619 | 3 | 6 | 9 | 13 | 16 |
| 5,3 | 16,650 | 16,682 | 16,713 | 16,745 | 16,776 | 16,808 | 16,839 | 16,870 | 16,902 | 16,933 | 3 | 6 | 9 | 13 | 16 |
| 5,4 | 16,965 | 16,996 | 17,027 | 17,059 | 17,090 | 17,122 | 17,153 | 17,185 | 17,216 | 17,247 | 3 | 6 | 9 | 13 | 16 |
| 5,5 | 17,279 | 17,310 | 17,342 | 17,373 | 17,404 | 17,436 | 17,467 | 17,499 | 17,530 | 17,562 | 3 | 6 | 9 | 13 | 16 |
| 5,6 | 17,593 | 17,624 | 17,656 | 17,687 | 17,719 | 17,750 | 17,781 | 17,813 | 17,844 | 17,876 | 3 | 6 | 9 | 13 | 16 |
| 5,7 | 17,907 | 17,938 | 17,970 | 18,001 | 18,033 | 18,064 | 18,096 | 18,127 | 18,158 | 18,190 | 3 | 6 | 9 | 13 | 16 |
| 5,8 | 18,221 | 18,253 | 18,284 | 18,316 | 18,347 | 18,378 | 18,410 | 18,441 | 18,473 | 18,504 | 3 | 6 | 9 | 13 | 16 |
| 5,9 | 18,535 | 18,567 | 18,598 | 18,630 | 18,661 | 18,692 | 18,724 | 18,755 | 18,787 | 18,818 | 3 | 6 | 9 | 13 | 16 |
| 6,0 | 18,850 | 18,881 | 18,912 | 18,944 | 18,975 | 19,007 | 19,038 | 19,069 | 19,101 | 19,132 | 3 | 6 | 9 | 13 | 16 |
| 6,1 | 19,164 | 19,195 | 19,227 | 19,258 | 19,289 | 19,321 | 19,352 | 19,384 | 19,415 | 19,446 | 3 | 6 | 9 | 13 | 16 |
| 6,2 | 19,478 | 19,509 | 19,541 | 19,572 | 19,604 | 19,635 | 19,666 | 19,698 | 19,729 | 19,761 | 3 | 6 | 9 | 13 | 16 |
| 6,3 | 19,792 | 19,823 | 19,855 | 19,886 | 19,918 | 19,949 | 19,981 | 20,012 | 20,043 | 20,075 | 3 | 6 | 9 | 13 | 16 |
| 6,4 | 20,106 | 20,138 | 20,169 | 20,200 | 20,232 | 20,263 | 20,295 | 20,326 | 20,358 | 20,389 | 3 | 6 | 9 | 13 | 16 |
| 6,5 | 20,420 | 20,452 | 20,483 | 20,515 | 20,546 | 20,577 | 20,609 | 20,640 | 20,672 | 20,703 | 3 | 6 | 9 | 13 | 16 |
| 6,6 | 20,735 | 20,766 | 20,797 | 20,829 | 20,860 | 20,892 | 20,923 | 20,954 | 20,986 | 21,017 | 3 | 6 | 9 | 13 | 16 |
| 6,7 | 21,049 | 21,080 | 21,112 | 21,143 | 21,174 | 21,206 | 21,237 | 21,269 | 21,300 | 21,331 | 3 | 6 | 9 | 13 | 16 |
| 6,8 | 21,363 | 21,394 | 21,426 | 21,457 | 21,488 | 21,520 | 21,551 | 21,583 | 21,614 | 21,646 | 3 | 6 | 9 | 13 | 16 |
| 6,9 | 21,677 | 21,708 | 21,740 | 21,771 | 21,803 | 21,834 | 21,865 | 21,897 | 21,928 | 21,960 | 3 | 6 | 9 | 13 | 16 |
| 7,0 | 21,991 | 22,023 | 22,054 | 22,085 | 22,117 | 22,148 | 22,180 | 22,211 | 22,242 | 22,274 | 3 | 6 | 9 | 13 | 16 |
| 7,1 | 22,305 | 22,337 | 22,368 | 22,400 | 22,431 | 22,462 | 22,494 | 22,525 | 22,557 | 22,588 | 3 | 6 | 9 | 13 | 16 |
| 7,2 | 22,619 | 22,651 | 22,682 | 22,714 | 22,745 | 22,777 | 22,808 | 22,839 | 22,871 | 22,902 | 3 | 6 | 9 | 13 | 16 |
| 7,3 | 22,934 | 22,965 | 22,996 | 23,028 | 23,059 | 23,091 | 23,122 | 23,154 | 23,185 | 23,216 | 3 | 6 | 9 | 13 | 16 |
| 7,4 | 23,248 | 23,279 | 23,311 | 23,342 | 23,373 | 23,405 | 23,436 | 23,468 | 23,499 | 23,531 | 3 | 6 | 9 | 13 | 16 |
| 7,5 | 23,562 | 23,593 | 23,625 | 23,656 | 23,688 | 23,719 | 23,750 | 23,782 | 23,813 | 23,845 | 3 | 6 | 9 | 13 | 16 |
| 7,6 | 23,876 | 23,908 | 23,939 | 23,970 | 24,002 | 24,033 | 24,065 | 24,096 | 24,127 | 24,159 | 3 | 6 | 9 | 13 | 16 |
| 7,7 | 24,190 | 24,222 | 24,253 | 24,285 | 24,316 | 24,347 | 24,379 | 24,410 | 24,442 | 24,473 | 3 | 6 | 9 | 13 | 16 |
| 7,8 | 24,504 | 24,536 | 24,567 | 24,599 | 24,630 | 24,662 | 24,693 | 24,724 | 24,756 | 24,787 | 3 | 6 | 9 | 13 | 16 |
| 7,9 | 24,819 | 24,850 | 24,881 | 24,913 | 24,944 | 24,976 | 25,007 | 25,038 | 25,070 | 25,101 | 3 | 6 | 9 | 13 | 16 |
| 8,0 | 25,133 | 25,164 | 25,196 | 25,227 | 25,258 | 25,290 | 25,321 | 25,353 | 25,384 | 25,415 | 3 | 6 | 9 | 13 | 16 |
| 8,1 | 25,447 | 25,478 | 25,510 | 25,541 | 25,573 | 25,604 | 25,635 | 25,667 | 25,698 | 25,730 | 3 | 6 | 9 | 13 | 16 |
| 8,2 | 25,761 | 25,792 | 25,824 | 25,855 | 25,887 | 25,918 | 25,950 | 25,981 | 26,012 | 26,044 | 3 | 6 | 9 | 13 | 16 |
| 8,3 | 26,075 | 26,107 | 26,138 | 26,169 | 26,201 | 26,232 | 26,264 | 26,295 | 26,327 | 26,358 | 3 | 6 | 9 | 13 | 16 |
| 8,4 | 26,389 | 26,421 | 26,452 | 26,484 | 26,515 | 26,546 | 26,578 | 26,609 | 26,641 | 26,672 | 3 | 6 | 9 | 13 | 16 |
| 8,5 | 26,704 | 26,735 | 26,766 | 26,797 | 26,829 | 26,861 | 26,892 | 26,923 | 26,955 | 26,986 | 3 | 6 | 9 | 13 | 16 |
| 8,6 | 27,018 | 27,049 | 27,081 | 27,112 | 27,143 | 27,175 | 27,206 | 27,238 | 27,269 | 27,300 | 3 | 6 | 9 | 13 | 16 |
| 8,7 | 27,332 | 27,363 | 27,395 | 27,426 | 27,458 | 27,469 | 27,520 | 27,552 | 27,583 | 27,615 | 3 | 6 | 9 | 13 | 16 |
| 8,8 | 27,646 | 27,677 | 27,709 | 27,740 | 27,772 | 27,803 | 27,835 | 27,866 | 27,897 | 27,929 | 3 | 6 | 9 | 13 | 16 |
| 8,9 | 27,960 | 27,992 | 28,023 | 28,054 | 28,086 | 28,117 | 28,149 | 28,180 | 28,212 | 28,243 | 3 | 6 | 9 | 13 | 16 |
| 9,0 | 28,274 | 28,306 | 28,337 | 28,369 | 28,400 | 28,431 | 28,463 | 28,494 | 28,526 | 28,557 | 3 | 6 | 9 | 13 | 16 |
| 9,1 | 28,588 | 28,620 | 28,651 | 28,683 | 28,714 | 28,746 | 28,777 | 28,808 | 28,840 | 28,871 | 3 | 6 | 9 | 13 | 16 |
| 9,2 | 28,903 | 28,934 | 28,965 | 28,997 | 29,028 | 29,060 | 29,091 | 29,123 | 29,154 | 29,185 | 3 | 6 | 9 | 13 | 16 |
| 9,3 | 29,207 | 29,248 | 29,280 | 29,311 | 29,342 | 29,374 | 29,405 | 29,437 | 29,468 | 29,500 | 3 | 6 | 9 | 13 | 16 |
| 9,4 | 29,531 | 29,562 | 29,594 | 29,625 | 29,657 | 29,688 | 29,719 | 29,751 | 29,782 | 29,814 | 3 | 6 | 9 | 13 | 16 |
| 9,5 | 29,845 | 29,877 | 29,908 | 29,939 | 29,971 | 30,002 | 30,034 | 30,065 | 30,096 | 30,128 | 3 | 6 | 9 | 13 | 16 |
| 9,6 | 30,159 | 30,191 | 30,222 | 30,254 | 30,285 | 30,316 | 30,348 | 30,379 | 30,411 | 30,442 | 3 | 6 | 9 | 13 | 16 |
| 9,7 | 30,473 | 30,505 | 30,536 | 30,568 | 30,599 | 30,631 | 30,662 | 30,693 | 30,725 | 30,756 | 3 | 6 | 9 | 13 | 16 |
| 9,8 | 30,788 | 30,819 | 30,850 | 30,882 | 30,913 | 30,945 | 30,976 | 31,008 | 31,039 | 31,070 | 3 | 6 | 9 | 13 | 16 |
| 9,9 | 31,102 | 31,133 | 31,165 | 31,196 | 31,227 | 31,259 | 31,290 | 31,322 | 31,353 | 31,385 | 3 | 6 | 9 | 13 | 16 |
| 10,0 | 31,416 | ||||||||||||||
| d | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 1 | 2 | 3 | 4 | 5 |
Расчет веса
С расчетом веса трубы все просто: надо знать, сколько весит погонный метр, затем эту величину умножить на длину в метрах. Вес круглых стальных труб есть в справочниках, так как этот вид металлопроката стандартизован. Масса одного погонного метра зависит от диаметра и толщины стенки. Один момент: стандартный вес дан для стали плотностью 7,85 г/см2 — это тот вид, который рекомендован ГОСТом.
В таблице Д — наружный диаметр, условный проход — внутренний диаметр, И еще один важный момент: указана масса обычных стального проката, оцинкованные на 3% тяжелее.
Что следует знать о размерах
И в заключение – немного полезной информации. Обычно трубы имеют стандартные размеры, которые выражаются в дюймах. Для перевода значения из сантиметров в дюймы и обратно пользуемся следующими соотношениями: 1 дюйм = 2,54 см; 1 см = 0,398 дюйма. Но чтобы не ошибиться при выборе труб, необходимо учитывать один важный нюанс. Например, когда речь идет о водопроводной трубе в 1 дюйм (обозначается – 1″), то имеется ввиду не наружный ее диаметр, а так называемый условный проход трубы, который ближе по своему значению ко внутреннему диаметру. Под условным проходом следует понимать средний внутренний диаметр, округленный до значений стандартного ряда: 6, 8, 10, 15, 20, 25, 32, 40, 50, 65, 80, 100, 125, 150, 200, 250, 300, 350, 400, 500, 600, 800, 1000, 1200, 1400, 1600, 2000, 2400, 3000 мм. Для лучшего понимания этого нюанса и для удобства конвертации размеров можно воспользоваться следующей таблицей.
В таблице представлены размеры до 6″, так как большие вам навряд ли понадобятся. Значения наружного диаметра могут немного отличатся от табличных, в зависимости от разных типов изделий.
При строительстве и обустройстве дома трубы не всегда используются для транспортировки жидкостей или газов. Часто они выступают как строительный материал — для создания каркаса различных построек, опор для навесов и т.д. При определении параметров систем и сооружений необходимо высчитать разные характеристики ее составляющих. В данном случае сам процесс называют расчет трубы, а включает он в себя как измерения, так и вычисления.
Измерение труб с помощью фотосъемки (метод копирования)
Этот нестандартный метод применяется при полной недоступности к трубе любого размера. К измеряемой трубе прикладывают линейку или любой другой предмет, размеры которого заранее известны любому мастеру (часто в этом случае используют спичечный коробок, длина которого составляет 5 см, или монету). Далее этот участок трубы с приложенным предметом фотографируют (кроме фотоаппарата в современных условиях доступно использование и мобильного телефона). Следующие вычисления размеров производятся по фотоснимкам: на снимке измеряют визуальную толщину в мм, а затем переводят ее в реальные значения, учитывая масштаб фотографий.
Контроль параметров труб в производственных условиях
Наружный диаметр водопроводных или канализационных труб в условиях больших производств контролируют и проверяют с применением более усложненной формулы: D = L:3,14 — 2∆p — 0,2 мм.
В этой формуле, кроме уже известных значений, символы ∆p означают толщину полотна рулетки в мм, которую вы применяете для измерений диаметра, а «0,2 мм» из формулы – это допустимые отклонения, учитывающие прилегание рулетки к трубе. Значение допустимого отклонения для труб сечением 200 мм составляет ±1,5 мм.
При замерах труб большого диаметра допустимые отклонения измеряются в процентах. Пример, для изделий размером от 820 до 1020 мм допустимое отклонение = 0,7%. При таких замерах используется измерительная установка на основе ультразвука.
Толщину стенок труб в условиях больших производств измеряют штангенциркулем с делением шкалы 0,01 мм. Допустимое отклонение от номинальной толщины в сторону уменьшения не должен превышать 5%.
Контролю подлежат и значения кривизны трубы, которые не должны быть выше 1,5 мм на погонный метр длины трубы. Общая кривизна изделий по отношению к ее длине не должна составлять более 0,15%. Овальность трубных торцов определяется отношением разности наибольшего и наименьшего диаметра к номинальному диаметру трубы.
Значение этого параметра не должен превышать 1% для труб с толщиной стенки до 20 мм и не выше 0,8% для стенок выше 20 мм.
Овальность трубы можно определить, измерив диаметр торца трубы с помощью индикаторной скобы или нутромера в двух взаимно перпендикулярных плоскостях.
Несложные школьные познания и внимательное применение простых инструментов существенно упростят вашу задачу — как измерить диаметр трубы подручными средствами.
[spoiler title=”источники:”]
http://poschitat.online/dlina-okruzhnosti
http://b4.cooksy.ru/articles/dlina-okruzhnosti-cherez-storony-treugolnika
[/spoiler]
8 способов найти длину окружности
Выбирайте формулу, ориентируясь на известные величины.
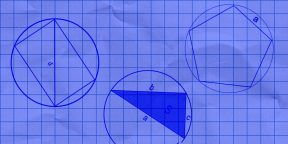
1. Как найти длину окружности через диаметр
Просто умножьте диаметр на число пи.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- d —диаметр окружности.
2. Как найти длину окружности через радиус
Умножьте число пи на два радиуса.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- r — радиус окружности.
3. Как вычислить длину окружности через площадь круга
Умножьте число пи на четыре площади круга.
Найдите корень из результата.
- O — искомая длина окружности.
- S – площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
4. Как найти длину окружности через диагональ вписанного прямоугольника
Умножьте число пи на диагональ.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- d – любая диагональ прямоугольника.
5. Как вычислить длину окружности через сторону описанного квадрата
Умножьте число пи на сторону квадрата.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- a – любая сторона квадрата.
6. Как найти длину окружности через стороны и площадь вписанного треугольника
Перемножьте стороны треугольника.
Поделите результат на площадь и на два.
Умножьте полученное число на пи.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- S – площадь треугольника.
- a, b, c – стороны треугольника.
7. Как найти длину окружности через площадь и полупериметр описанного треугольника
Поделите площадь треугольника на его полупериметр.
Умножьте результат на число пи и на два.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- S – площадь треугольника.
- p – полупериметр треугольника (равен половине от суммы всех сторон).
8. Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разделите 180 градусов на количество сторон многоугольника.
Найдите синус полученного числа.
Разделите сторону многоугольника на результат.
Умножьте получившееся число на пи.
- O — искомая длина окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- π (пи) — константа, равная 3,14.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✏️🎓
- Как найти периметр прямоугольника
- 8 способов найти периметр треугольника
- 7 способов найти площадь прямоугольника
- Как перевести обычную дробь в десятичную
- Как освоить устный счёт школьникам и взрослым
Длина (периметр) окружности калькулятор онлайн умеет вычислять длину восемью способами:
- По радиусу.
- По диаметру.
- По площади окружности.
- По диагонали вписанного прямоугольника.
- По стороне описанного квадрата.
- По сторонам и площади описанного треугольника.
- По площади вписанного треугольника.
- По стороне вписанного многогранника.
Сделав расчет периметра на этом онлайн калькуляторе Вы получите не только ответ, но и детальное, пошаговое решение с выводом формул и промежуточных действий.
Длина окружности или периметр окружности – это длина кривой из множества точек которая ограничивает собой круг.
Длина окружности может быть найдена по длине пути, который проедет круг сделав один полный оборот.
Как найти длину окружности?
Найти длину окружности очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
1) По радиусу
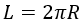
где R – радиус окружности.
2) По диаметру
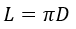
где D – диаметр окружности.
3) По площади окружности
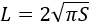
ггде S – площадь окружности.
4) По диагонали вписанного прямоугольника
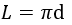
где d – диагональ вписанного прямоугольника.
5) По стороне описанного квадрата
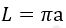
где a – сторона описанного квадрата.
6) По сторонам и площади описанного треугольника
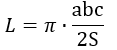
где a,b,c – стороны описанного треугольника, S – его площадь.
7) По площади вписанного треугольника
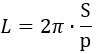
где p – полупериметр вписанного треугольника, S – его площадь.
8) По стороне вписанного многогранника
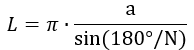
где a – сторона вписанного многогранника, N – количество сторон.
Скачать все формулы в формате Word
Длина окружности по стороне вписанного правильного треугольника
Калькулятор рассчитывает длину окружности по стороне вписанного в неё правильного треугольника.
Введите сторону треугольника a
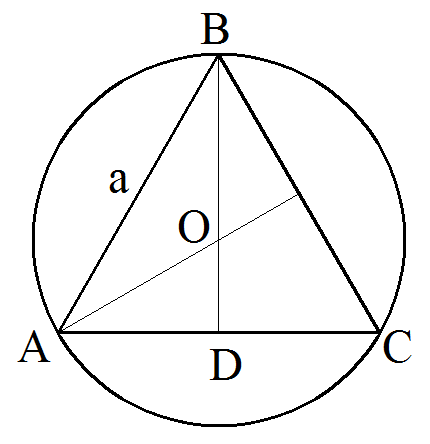
Формула длины окружности по стороне вписанного в неё правильного треугольника
Т.к. в равностороннем треугольнике медианы равны и в точке пересечения делятся в отношении 2:1. А точка пересечения будет центром окружности.
Из этого следует что нам нужно найти радиус окружности, а он будет равен 2/3 от медианы(высоты) BD.
По теореме Пифагора найдём BD.
Подставим полученный радиус в формулу окружности по радиусу
Где a – сторона правильного треугольника, π=3.1415926536
Разберём пример
Дана окружность с вписанным в неё правильным треугольником. Сторона треугольника равна 10. Необходимо найти длину окружности.
Похожие калькуляторы
Содержание материала
- Как найти длину отрезка (расстояние между точками) с помощью онлайн-калькулятора
- Видео
- Как найти длину окружности через стороны и площадь вписанного треугольника
- Свойства и линии
- Как вычислить длину окружности через сторону вписанного правильного многоугольника
- Как найти длину окружности
- Разбор примера
- Разбор примера
- Хорда и дуга окружности
Как найти длину отрезка (расстояние между точками) с помощью онлайн-калькулятора
Рассмотрим пример, наглядно демонстрирующий работу с онлайн-калькулятором. Найдем длину произвольного отрезка, начальная и конечная точки которого имеют координаты (1;4) и (3;0). Для этого:
- Выберем размерность (2 или 3). Калькулятор позволяет задать отрезок соответственно на плоскости, или в пространстве. В нашем конкретном примере выберем плоскость (2):

- Введем в пустые поля координаты начальной и конечной точек отрезка:

- После ввода координат остается нажать «Рассчитать» и получить ответ с решением:

Видео
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:

где:
π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника 
Свойства и линии
Из-за того, что прямоугольник — это параллелограмм, все свойства последнего справедливы и к нему. В первую очередь для него характерно, что противоположные стороны являются параллельными, то есть лежат на непересекающихся прямых. Отсюда следует, что фигуры отличаются друг от друга только размерами двух граней.
К основным свойствам прямоугольника относят:
- противолежащие стороны имеют равную длину: AB = CD, BC = AD;
- все углы равны 90 градусов;
- отрезки, обозначающие ширину и длину, всегда перпендикулярные друг другу: AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB;
- сумма любых двух углов фигуры равняется 180 градусов, соответственно всех четырёх — 360;
- в четырёхугольном теле можно провести 2 диагонали, длины которых будут совпадать по величине: AB = BC;
- сумма квадратов диагональных отрезков равняется удвоенной сумме квадратов сторон фигуры: AC2 + BD2 = 2 (AB2 + BC2);
- построенная диагональ разделяет прямоугольник на 2 одинаковые фигуры — прямоугольные треугольники;
- точка пересечения прямых линий, соединяющая попарно противоположные углы, является центром фигуры и описанной окружности;
- диагонали в месте пересечения разделяются на 4 равных отрезка;
- в многоугольник, у которого длина не равна ширине, вписать окружность нельзя, поэтому её можно построить только для частных случаев прямоугольника.
На свойстве, что сложенные квадраты диагоналей можно найти как сумму квадратов всех его сторон, построено решение многих геометрических задач. Нелишним будет доказательство теоремы. Пусть имеется прямоугольник, у которого линии AC и BD — диагонали. Если изобразить многоугольник на рисунке и построить отрезки, можно увидеть, что каждая диагональ делит фигуру на 2 треугольника: ABC и BDC.
Используя теорему косинусов, можно записать: AC2 = AB2 + BC2 — 2 * AB * BC * cos (ABC); BD2 = CD2 + BC2 — 2 * CD * BC * cos (BCD). После сложения полученных выражений получится запись: AC2 + BD2 = AB2 + BC2 — 2 * AB * BC * cos (ABC) + CD2 + BC2 — 2 * CD * BC * cos (BCD).
Так как по свойству прямоугольной фигуры противоположные стороны равны, уравнение примет вид: AC2 + BD2 = 2AB2 + 2BC2 — 2 * AB * BC * cos (ABC) — 2 * AB * BC * cos (BCD). Учитывая, что сумма двух углов равняется 180, полученное выражение можно переписать так: AC2 + BD 2 = 2 (AB 2 + BC 2). Что и следовало доказать.
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата. Формула вычисления длины окружности: 
где:
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника 
Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Разбор примера
Условие задачи:
Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.
Воспользуемся формулой длины окружности: C = 2πR ≈ 2 · 3,14 · 24 ≈ 150,72 см
Разберем обратную задачу, когда мы знаем длину окружности, а нас просят найти её диаметр.
Разбор примера
Условие задачи:
Определите диаметр окружности, если её длина равна 56,52 дм. (π ≈ 3,14).
Выразим из формулы длины окружности диаметр.
C = πD D = С / π D = 56,52 / 3,14 = 18 дм
Хорда и дуга окружности
На рисунке ниже отметим на окружности две точки «A» и «B». Эти точки делят окружность на две части, каждую из которых называют дугой. Это синяя дуга «AB» и черная дуга «AB». Точки «A» и «B» называют концами дуг.
Соединим точки «A» и «B» отрезком. Полученный отрезок называют хордой.
 Важно!
Важно! 
Точки «A» и «B» делят окружность на две дуги. Поэтому важно понимать, какую дугу вы имеете в виду, когда пишите дуга «AB». Для того чтобы избежать путаницы, часто вводят дополнительную точку на нужной дуге и обращаются к ней по трем точкам.
 Длина окружности. Число Пи Площадь круга Площадь сферы. Объём шара
Длина окружности. Число Пи Площадь круга Площадь сферы. Объём шара
