Перейти к содержанию
Длина эллипса (овала)
На чтение 1 мин
Эллипс – это множество точек плоскости, для которых сумма расстояний до фокусов эллипса постоянна и больше расстояния между фокусами.
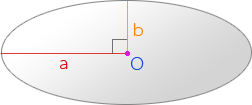
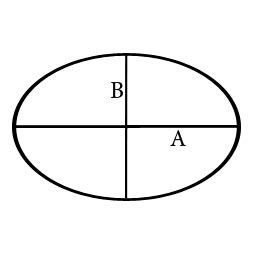
О – центр эллипса
Длина эллипса (L) равна произведению суммы его полуосей (a, b) на число π:
Вам также может понравиться
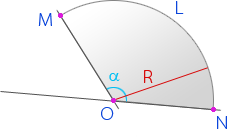
Дуга – это часть окружности, отсекаемая хордой.
0143
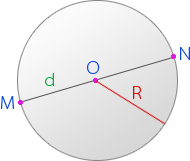
Окружность – геометрическое место точек, равноудаленных
0123
Окружность – геометрическое место точек, равноудаленных
0122
Многоугольник – это геометрическая фигура, которая
0141
Шестиугольник – это многоугольник, который имеет шесть углов.
0436
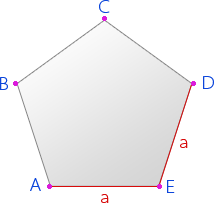
Пятиугольник – это многоугольник, который имеет пять углов.
0338
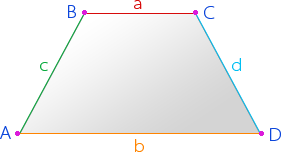
Трапеция – это четырехугольник, у которого параллельна
087
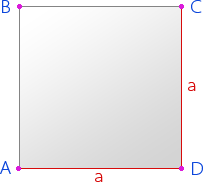
Квадрат – это параллелограмм, у которого все углы и
090
Калькулятор периметра эллипса
Введите длину большой и малой полуосей эллипса, укажите точность расчета и нажмите “Посчитать”. Калькулятор выполнит расчет периметра эллипса (расчет приблизительный).
Калькулятор
Эллипсом называется множество всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек F1 и F2 этой плоскости есть величина постоянная, больше расстояния между F1 и F2.
Точки F1 и F2 называют фокусами эллипса, а расстояние между ними – фокусным расстоянием.
Проходящий через фокусы эллипса отрезок, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a.
Отрезок, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
Точка пересечения большой и малой осей эллипса называется его центром.
Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
Формулу периметра эллипса нельзя выразить при помощи простейших функций.
Периметр эллипса
Эллипс — замкнутая кривая на плоскости, которая может быть получена как пересечение плоскости и кругового цилиндра или как ортогональная проекция окружности на плоскость. Окружность является частным случаем эллипса.
Приближённая формула для нахождения периметра эллипса:

Максимальная погрешность этой формулы
0,63% при эксцентриситете эллипса
0,988 (соотношение осей
1/6,5). Погрешность всегда положительная.
Используя этот онлайн калькулятор, вы сможете найти периметр эллипса, зная длину двух полуосей.
Онлайн калькуляторы
Calculatorium.ru – это бесплатные онлайн калькуляторы для самых разнообразных целей: математические калькуляторы, калькуляторы даты и времени, здоровья, финансов. Инструменты для работы с текстом. Конвертеры. Удобное решение различных задач – в учебе, работе, быту.
Актуальная информация
Помимо онлайн калькуляторов, сайт также предоставляет актуальную информацию по курсам валют и криптовалют, заторах на дорогах, праздниках и значимых событиях, случившихся в этот день. Информация из официальных источников, постоянное обновление.
Что такое эллипс: формула длины окружности эллипса
В астрономии, когда рассматривают движение космических тел по орбитам, часто применяют понятие “эллипс”, поскольку их траектории характеризуются именно этой кривой. Рассмотрим в статье вопрос, что представляет собой отмеченная фигура, а также приведем формулу длины эллипса.
Что такое эллипс?
Согласно математическому определению, эллипс – это замкнутая кривая, для которой сумма расстояний от любой ее точки до двух других определенных точек, лежащих на главной оси, и носящих название фокусов, является постоянной величиной. Ниже приведен рисунок, который поясняет это определение.

На рисунке сумма расстояний PF’ и PF равна 2 * a, то есть PF’ + PF = 2 * a, где F’ и F – фокусы эллипса, “a” – длина его большой полуоси. Отрезок BB’ называется малой полуосью, а расстояние CB = CB’ = b – длина малой полуоси. Здесь точка C определяет центр фигуры.
На рисунке выше также показан простой метод с веревкой и двумя гвоздиками, который широко используется для изображения эллиптических кривых. Другой способ получить эту фигуру заключается в выполнении сечения конуса под любым углом к его оси, который не равен 90o.
Если эллипс вращать вдоль одной из его двух осей, то он образует объемную фигуру, которая зазывается сфероидом.
Формула длины окружности эллипса
Хотя рассматриваемая фигура является достаточно простой, длину ее окружности точно можно определить, если вычислить так называемые эллиптические интегралы второго рода. Однако, индусский математик-самоучка Рамануджан еще в начале XX века предложил достаточно простую формулу длины эллипса, которая приближается к результату отмеченных интегралов снизу. То есть рассчитанное по ней значение рассматриваемой величины будет немного меньше, чем реальная длина. Эта формула имеет вид: P ≈ pi * [3 * (a+b) – √((3 * a + b) * (a + 3 * b))], где pi = 3,14 – число пи.
Например, пусть длины двух полуосей эллипса будут равны a = 10 см и b = 8 см, тогда его длина P = 56,7 см.
Каждый может проверить, что если a = b = R, то есть рассматривается обычная окружность, тогда формула Рамануджана сводится к виду P = 2 * pi * R.
Отметим, что в школьных учебниках часто приводится другая формула: P = pi * (a + b). Она является более простой, но и менее точной. Так, если ее применить для рассмотренного случая, то получим значение P = 56,5 см.
[spoiler title=”источники:”]
http://calculatorium.ru/math/ellipse-perimeter
http://1ku.ru/obrazovanie/10686-chto-takoe-ellips-formula-dliny-okruzhnosti-ellipsa/
[/spoiler]
Помогите рассчитать длину окружности овала
Ольга Кравцова
Знаток
(453),
закрыт
10 лет назад
Помогите, пожалуйста. Простой способ как нарисовать овал на прямоугольном отрезке ткани с помощью трех иголок и веревочки я знаю, а вот как найти длину его границы не знаю. Необходимо рассчитать длину окружности эллипса, который вписан в прямоугольник со сторонами 2,5м и 3,2м. Мне собственно говоря точные формулы не нужны, нужен сам результат, чтобы знать сколько метров ленты для окантовки купить. Это будет коврик для детской игры, если кому интересно.
Дополнен 10 лет назад
3,14*3,2=10,048
3,14*2,5=7,75
10,048-7,75=1,099
10,048-1,099=8,949 м.
Вот до чего я приблизительно дошла вспоминая школьную науку, но так ли это? Ау, кто силен в математике, помогите. 8,95м (или 9 метров если округлить) Верно?
tzorin_b
Мудрец
(12377)
10 лет назад
1) “Окружность овала” – звучит как-то странно.
2) Эллипс и овал – разные вещи. Если три иголки и веревочка – то, видимо, эллипс. Овал – это прямоугольник и два полукруга.
3) Это не школьный курс.
4) С точными формулами у эллипса проблема. Интегрально вычислять не полезу.
5) Проще ниточкой померить.
6) Если брать приблизительные формулы, то 4*(Pi*a*b+(a-b)*(a-b))/(a+b). Погрешность не более 0,63%. Источник – википедия. .
7) По этой формуле выходит примерно 8,99. С учетом погрешности – не более 9,05
8) Я не знаю, как у Вас вышел почти правильный ответ, но 10,048-7,75 никоим образом не равно 1,099.
настя
Мыслитель
(6093)
10 лет назад
Метод 1. Расчет длины окружности, исходя из знания ее радиуса. Радиусом окружности называется отрезок, соединяющий центр О с любой из точек окружности, например, R:
D = πR*2, где
R = OR – радиус этой окружности,
π – постоянное значение, равное, приблизительно, 3.14.
Метод 2. Вытекает из первого метода. Известно, что радиус окружности равен половине ее диаметра. Тогда рассчитать длину окружности можно будет по формуле:
D = πS, где
S – диаметр этой окружности. Диаметр окружности – это отрезок, проходящий через центр окружности О и соединяющие любые 2 противоположные между собой точки.
Ольга КравцоваЗнаток (453)
10 лет назад
В теле вопроса, я не формулы просила, а конечный результат. Но в любом случае, спасибо за старания
Seo Web
Профи
(865)
6 лет назад
Проще всего воспользоваться бесплатным калькулятором периметра эллипса (овала)
https://tamali.net/calculator/2d/ellipse/perimeter/
Для того, что бы узнать периметр эллипса или овала нам необходимо узнать длину двух полуосей или длину двух осей эллипса (максимальную и минимальную длину эллипса). После того как нам стали известны указанные величины мы можем применить формулу для расчета периметра эллипса:
P= 2π√a²+b²/2
формула для вычисления P – периметра по полуосям a, b
P= 2π√A²+B²/8
формула для вычисления P – периметра осям A, B
Казалось бы, что может быть проще. Обычная геометрическая фигура – эллипс. Но эта злодейка скрывает в себе нечто очень интересное и сложное…
Если, к примеру, периметр окружности, т.е. длину окружности можно легко найти по формуле:
То вот с периметром эллипса все многократно сложнее… Но, обо всем по порядку.
Эллипс – замкнутая кривая на плоскости, которая может быть получена сечением круглого цилиндра плоскостью.
Есть и более сложные определения, но, я думаю, они здесь ни к чему.
Каноническое уравнение эллипса, которое вписывается в декартову систему координат имеет такой вид:
Площадь эллипса найти не проблема, формула довольно простая, вот, пожалуйста:
Я подсчитал площадь в CAD-системе с помощью обычной заливки и вычислил на калькуляторе, значения идентичные:
А теперь, приготовьтесь к погружению в мир мук и страданий. Периметр или длина кривой, называйте как хотите…
Суть в том, что не существует абсолютно точной на 100% формулы, которая вычисляла бы периметр эллипса!
Если Вы попробуете поискать в сети, то найдет целую россыпь различных формул, которые с той или иной степенью точности вычисляют периметр эллипса. Самая простая из них выглядит следующим образом:
Без интеграла и на том спасибо… Но и через интеграл можно вычислить, если есть желание, точность будет чуть выше.
Я точно так же как и с площадью решил сравнить результаты непосредственных измерений в CAD системе и вычисленных по формуле и вот что вышло:
Как видите, даже близко не совпадение. Я не знаю, каким образом считает CAD-система длину кривой, но наверняка точность там близка к 100%…
Как я и писал, есть множество формул, которые с той или иной погрешностью считают периметр. Если у вас много времени и неуемное желание достигнуть недостижимое, то пару сот лет назад, шотландский математик Джеймс Айвори и немецкий математик и астроном Фридрих Бессель независимо друг от друг вывели самую точную, близкую к идеалу, формулу для вычисления периметра эллипса…
А теперь представьте, что на уроке геометрии Вам предлагают вместо контрольной вычислить периметр эллипса через эту формулу 🙂
Публикация создавалась в ознакомительно-развлекательных целях. Надеюсь, было интересно!
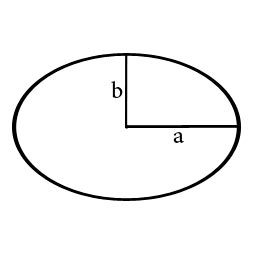
| Вычислить периметр эллипса через: | |
| Длина полуоси a: | |
| Длина полуоси b: | |
Для того, что бы узнать периметр эллипса нам необходимо узнать длину двух полуосей или длину двух осей эллипса (максимальную и минимальную длину эллипса). После того как нам стали известны указанные величины мы можем применить формулу для расчета периметра эллипса:
P= 2π
√
(a2+b2)/2
формула для вычисления P – периметра по полуосям a, b
P= 2π
√
(A2+B2)/8
формула для вычисления P – периметра осям A, B
Где P – периметр, a и b – полуоси, A и B – оси эллипса, π – число Пи которое всегда примерно равно 3,14.