Длина окружности
Длина окружности
Длина любой окружности больше своего диаметра в одно и то же число раз, а именно, приблизительно в 3,14 раза. Для обозначения этой величины используется маленькая (строчная) греческая буква π (пи):
Таким образом, длину окружности (C) можно вычислить, умножив константу π на диаметр (D), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
где C — длина окружности, π — константа, D — диаметр окружности, R — радиус окружности.
Так как окружность является границей круга, то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Решение: Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см).
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Решение: Сначала найдём диаметр окружности, умножив длину радиуса на 2:
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м).
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Решение: Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π:
следовательно, радиус будет равен:
| R | ≈ | 7,85 | = | 7,85 | = 1,25 (м). |
| 2 · 3,14 | 6,28 |
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Решение: Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2 ).
Ответ: 12,56 см 2 .
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Решение: Сначала найдём радиус круга, разделив его диаметр на 2:
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2 ).
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 · | 7 2 | = 3,14 · | 49 | = |
| 4 | 4 | 4 |
| = | 153,86 | = 38,465 (см 2 ). |
| 4 |
Ответ: 38,465 см 2 .
Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .
Решение: Чтобы найти радиус круга по его площади, надо площадь круга разделить π, а затем из полученного результата извлечь квадратный корень:
Длина окружности
О чем эта статья:
6 класс, 9 класс, ЕГЭ/ОГЭ
Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так – l
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Как найти длину окружности через диаметр
Хорда — это отрезок, который соединяет две точки окружности.
Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:
π— число пи — математическая константа, примерно равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, примерно равное 3,14
r – радиус окружности
Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, примерно равное 3,14
S — площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, примерно равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
π – математическая константа, примерно равная 3,14
a – сторона квадрата
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, примерно равная 3,14
S — площадь треугольника
p — полупериметр треугольника
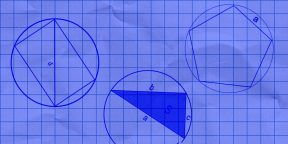
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен Подставим туда наши переменные и получим
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Обучение на курсах по математике поможет закрепить полученные знания на практике.
“Окружность. Длина окружности”, 5-й класс
Разделы: Математика
Класс: 5
Оборудование:
- Игрушечные автомобили с различным диаметром колеса;
- мерки – тесьма или нить.
- линейки.
- листы бумаги с таблицей вида:
Группа С S d C/d
Все перечисленное раздать по количеству подгрупп.
План оформления доски:
| Задача 1. | Окружность
|
Таблица | Задача 2. |
Таблица:
| Группа № | С (длина окружности) | S (путь) | d (диаметр колеса) |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| Т.Н. |
Цель: повторить понятие окружности, ее диаметра; получить формулу длины окружности и научить применять ее при решении задач, число π.
Ход урока
1. Анализ заданий
| Учитель | Дети |
| – На доске изображена геометрическая фигура. Как она называется? | – Окружность. |
| – Дайте определение окружности. | Окружность – это замкнутая линия, все точки которой равноудалены от одной, называемой центром окружности. |
| – Что мы называем ее радиусом? | – Радиус – это расстояние от центра до любой точки окружности. |
| – Что мы называем ее диаметром? | – Диаметр – это отрезок, соединяющий 2 точки окружности и проходящий через центр. |
| – Каким соотношением связаны между собой диаметр и радиус? | – d=2r |
| – Что мы знаем о размере всех d, всех r одной окружности? | – Они равны между собой. |
| –Нам трудно представить свою жизнь без окружности, ведь она является математической моделью многих окружающих нас предметов. Приведите примеры. | – Баранка, обруч, колесо и тд. |
2. Постановка проблемы
| Учитель | Дети |
| –На каждом столе автомашины, моделью каких их частей является окружность? | – Руль, колесо, обода фар и тд. |
| Вашему вниманию предлагается следующая задача (задача 1): Какой путь пройдет ваш автомобиль, если его правое колесо сделает 200 оборотов?Какие варианты решения? |
– Измерить длину окружности, проходящей по поверхности колеса и умножить ее на 200. |
| – Молодцы, но для того, чтобы не забыть измеренные величины, я прошу вас записать их в таблицу, лежащую перед вами. А чтобы иметь возможность обобщить эти результаты, я буду заполнять сводную таблицу на доске. |
(проводятся измерения, вычисления, заполняются таблицы и сводная таблица на доске (графы С и S)). |
| – Почему получили различные длины окружностей? | – Различные размеры колес. |
| – От чего зависит размер? | – От диаметра. |
| – Молодцы. В Республике Беларусь есть город Жодино. Он известен тем, что там расположен завод, выпускающий карьерные самосвалы марки «БелАз», грузоподъемностью 720 тонн (грузоподъемность Жигулей 440 кг). Внимание вопрос: какой путь пройдет такой самосвал, если правое переднее колесо делает 200 оборотов (диаметр колеса 3,7 метров)? (Задача 2 на доске была закрыта) |
– Не знаем как найти длину окружности, чтобы умножить ее на количество оборотов. |
| – Но нам дан диаметр. | – Но неизвестна формула, связывающая диаметр и длину окружности. |
| – Значит, для решения задачи нам нужно установить связь между диаметром и длиной окружности.Значит, тема сегодняшнего урока… | – Нахождение длины окружности, если известен ее диаметр. |
3. Выход из проблемной ситуации
| Учитель | Дети |
| – Измерьте диаметр колес вашего автомобиля. Занесите его в таблицу. | |
| – У каждого автомобиля самая большая длина окружности колеса? | – У того, у кого диаметр больше |
| – Какой вывод можно сделать? | – Чем больше диаметр, тем больше длина окружности. |
| – Посчитайте чему равно отношение С к d? | – Во всех случаях С/d=3 |
| – Оказывается, что если посчитать точнее, то С/d=3, 1/7=3,14159265 C/d=π, C=πd D=2r, C=2 πr |
– π=C/d=3,14 |
| – Как связаны между собой d и с? | – Прямопропорционально. |
| – Мы получили формулы, которые связывают длину окружности с диаметром, теперь мы можем вернуться к нашей задаче. S=C*n C=π*d=3,14*3,7=11,618 метров S=2323,6 метров. Значит, чтобы найти длину любой окружности надо знать радиус и знать формулу: C=2πr |
– Каждая группа считает самостоятельно |
4. Закрепление пройденного
Найти длину окружности, изображенной на рисунке 12, №№ 850, 851, 852.
Домашнее задание: №№ 868, 869, 873(а,б), 866.
5. Итог урока
чему научились сегодня на уроке? (Находить длину любой окружности, зная ее диаметр по формуле: С=π*d.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/dlina-okruzhnosti
http://urok.1sept.ru/articles/521138
[/spoiler]
8 способов найти длину окружности
Выбирайте формулу, ориентируясь на известные величины.
1. Как найти длину окружности через диаметр
Просто умножьте диаметр на число пи.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- d —диаметр окружности.
2. Как найти длину окружности через радиус
Умножьте число пи на два радиуса.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- r — радиус окружности.
3. Как вычислить длину окружности через площадь круга
Умножьте число пи на четыре площади круга.
Найдите корень из результата.
- O — искомая длина окружности.
- S – площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
4. Как найти длину окружности через диагональ вписанного прямоугольника
Умножьте число пи на диагональ.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- d – любая диагональ прямоугольника.
5. Как вычислить длину окружности через сторону описанного квадрата
Умножьте число пи на сторону квадрата.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- a – любая сторона квадрата.
6. Как найти длину окружности через стороны и площадь вписанного треугольника
Перемножьте стороны треугольника.
Поделите результат на площадь и на два.
Умножьте полученное число на пи.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- S – площадь треугольника.
- a, b, c – стороны треугольника.
7. Как найти длину окружности через площадь и полупериметр описанного треугольника
Поделите площадь треугольника на его полупериметр.
Умножьте результат на число пи и на два.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- S – площадь треугольника.
- p – полупериметр треугольника (равен половине от суммы всех сторон).
8. Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разделите 180 градусов на количество сторон многоугольника.
Найдите синус полученного числа.
Разделите сторону многоугольника на результат.
Умножьте получившееся число на пи.
- O — искомая длина окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- π (пи) — константа, равная 3,14.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✏️🎓
- Как найти периметр прямоугольника
- 8 способов найти периметр треугольника
- 7 способов найти площадь прямоугольника
- Как перевести обычную дробь в десятичную
- Как освоить устный счёт школьникам и взрослым
Возьмем циркуль. Установим ножку циркуля с иглой в точку «O», а ножку циркуля с
карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую
линию. Такую замкнутую линию называют — окружность.
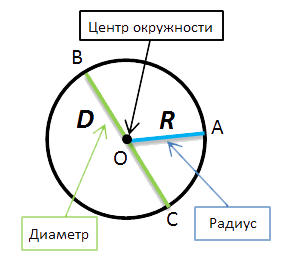
Рассмотрим более подробно окружность. Разберёмся, что называют центром,
радиусом и диаметром окружности.
- (·)O — называется центром окружности.
- Отрезок, который соединяет
центр и любую точку окружности, называется радиусом окружности.
Радиус окружности обозначается буквой «R». На рисунке выше —
это отрезок «OA». - Отрезок, который соединяет
две точки окружности и проходит через её центр, называется
диаметром окружности.Диаметр окружности обозначается буквой «D».
На рисунке выше — это отрезок «BC».На рисунке также видно, что диаметр равен двум радиусам. Поэтому
справедливо выражение «D = 2R».
Число π и длина окружности
Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что
такое число π (читается как «Пи»), которое
так часто упоминают на уроках.
В далекие времена математики Древней Греции внимательно изучали окружность
и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.
Запомните!
Отношение длины окружности к её диаметру является одинаковым
для всех
окружностей и обозначается греческой буквой π
(«Пи»).
π ≈ 3,14…
Число «Пи» относится к числам, точное значение которых записать невозможно
ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам
для наших вычислений достаточно использовать значение π,
округленное до разряда сотых
π ≈ 3,14…
Теперь, зная, что такое число π, мы
можем записать формулу длины окружности.
Запомните!
Длина окружности
— это произведение числа π
и диаметра окружности.
Длина окружности обозначается буквой «С» (читается как «Це»).
C = πD
C = 2πR
, так как D = 2R
Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Разбор примера
Условие задачи:
Найдите длину окружности, радиус которой равен 24 см. Число
π
округлите до сотых.
Воспользуемся формулой длины окружности:
C = 2πR
≈ 2 · 3,14 · 24 ≈ 150,72 см
Разберем обратную задачу, когда мы знаем длину
окружности, а нас просят найти её диаметр.
Разбор примера
Условие задачи:
Определите диаметр окружности, если
её длина равна 56,52 дм.
(π ≈ 3,14).
Выразим из формулы длины окружности диаметр.
C = πD
D = С / π
D = 56,52 / 3,14 = 18 дм
Хорда и дуга окружности
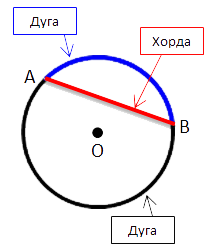
На рисунке ниже отметим на окружности две точки «A» и «B». Эти точки делят окружность
на две части, каждую из которых называют дугой.
Это синяя дуга «AB» и черная дуга «AB».
Точки «A» и «B» называют концами дуг.
Соединим точки «A» и «B» отрезком. Полученный отрезок называют
хордой.
Важно!
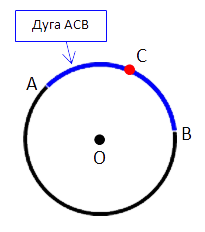
Точки «A» и «B» делят окружность на две дуги. Поэтому важно
понимать, какую дугу вы имеете в виду, когда пишите дуга «AB».
Для того чтобы избежать путаницы, часто вводят дополнительную точку на
нужной дуге и обращаются к ней по трем точкам.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 мая 2020 в 10:27
Владислав Заступневич
Профиль
Благодарили: 0
Сообщений: 1
Владислав Заступневич
Профиль
Благодарили: 0
Сообщений: 1
, Радиус одной окружности равен 12 см, а второй-36см.Чему равно отношения длины первой окружности к длине второй окружности?
0
Спасибо
Ответить
6 мая 2020 в 15:48
Ответ для Владислав Заступневич
Галина Федотова
Профиль
Благодарили: 0
Сообщений: 3
Галина Федотова
Профиль
Благодарили: 0
Сообщений: 3
С=2πR
если длину одной окружности разделить на дилну другой, то 2π сократится, следовательно длины будут относится так же как радиусы, то есть 12:36=
0
Спасибо
Ответить
22 сентября 2016 в 19:03
Вика Камалова
Профиль
Благодарили: 0
Сообщений: 2
Вика Камалова
Профиль
Благодарили: 0
Сообщений: 2
Помогите 2) чему равен деаметр если радиус равен а)12см б)10 децеметров
1) начертить окружность радиусом а)2 см пот буквой б)4см 5мм (начертиь!)
3)Чему равен радиус если деаметр равен а)6см б)9см в)12мСРОЧНО СЕГОДНЯ! ПРОШУ!!!
0
Спасибо
Ответить
23 сентября 2016 в 14:51
Ответ для Вика Камалова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Радиус равен половине диаметра. Обратно диаметр равен двум радиусам. Подробнее здесь.
1) а) 12см · 2=24см б)10дм · 2 = 20дм
2) ответил в теме.
3) а) 6см: 2 = 3см б) 9см: 2 = 4см 5 мм в)12м: 2 = 6м
0
Спасибо
Ответить
22 сентября 2016 в 18:54
Вика Камалова
Профиль
Благодарили: 0
Сообщений: 2
Вика Камалова
Профиль
Благодарили: 0
Сообщений: 2
1)Начертить окружность радиусом а)2 см пот буквой б)4 см 5 мм
0
Спасибо
Ответить
23 сентября 2016 в 14:46
Ответ для Вика Камалова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Радиус окружности это расстояние от центра до любой точки окружности. Подробнее можно посмотреть вот здесь. На линейке циркулем отмеряем необходимый радиус и чертим окружность.
0
Спасибо
Ответить
24 января 2016 в 13:45
Инна Шабрашина
Профиль
Благодарили: 0
Сообщений: 5
Инна Шабрашина
Профиль
Благодарили: 0
Сообщений: 5
Длина окружности и площадь круга.
Я не понимаю как найти площадь круга.
0
Спасибо
Ответить
19 сентября 2016 в 10:56
Ответ для Инна Шабрашина
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
0
Спасибо
Ответить
7 сентября 2015 в 21:08
Игорь Желтоновский
Профиль
Благодарили: 0
Сообщений: 1
Игорь Желтоновский
Профиль
Благодарили: 0
Сообщений: 1
радиус — 2,1 м.Найти длинну круга и его площадь(помогите плз)
0
Спасибо
Ответить
2 сентября 2016 в 15:18
Ответ для Игорь Желтоновский
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Длина окружности(l) вычисляется по формуле: l=2?r
Площадь круга(S) вычисляется по формуле: S=?r2
Подставляем значения и считаем, приняв ?=3,14
l=2 · 3,14 · 2,1 = 13,188
S = 3,14 · 2,12=13,8474
Более подробно можно прочитать здесь: math-prosto.ru/index.php?page=pages/circle/square_of_circle.php
0
Спасибо
Ответить
Сегодня мы говорим про окружность и круг, друзья мои. У многих шестиклассников, да и не только у них, возникают трудности с этой темой. А она-то как раз и есть ваш реальный шанс на получение хорошей отметки. Да, есть там одна заковырка. Вот она не нравится ребятам. Но я сейчас подробно всё расскажу. Давайте приступим)))
Сначала дам несколько определений. Они очень лёгкие, просто посмотрите:
Есть окружность, а есть круг:
Определения, ребята, есть у вас в учебнике. Их надо знать наизусть, учителя это любят. Выучите их, пожалуйста. А я вам простыми словами расскажу, чтобы совсем понятно было.
- Окружность – это линия на бумаге или ещё где-нибудь. На асфальте мелом, например.
- Круг – это часть листа (плоскости).
Как отличить круг от окружности?
Круг я могу вырезать ножницами и у меня в руках будет круглый кусок бумаги. А линию я вам как вырежу?!
Окружность нельзя вырезать ножницами! Она же линия!
Дальше. У вас будут две формулы. Я знаю, что их три, на самом деле – две. Расскажу попозже. Сначала основные определения простыми словами дам:
А это диаметр. Присмотритесь: вам ничего не показалось?)))
Вы молодцы, если вам показалось, что один диаметр – это ДВА РАДИУСА! Так и есть!
Значит, вот эти две формулы одинаковые.
Запомните: один диаметр – это два радиуса! Один радиус – это половина диаметра! Если знаете диаметр – радиус тоже знаете!!! И наоборот!
Что такое C в этой формуле? Это длина окружности. Если я возьму окружность, мысленно её разрежу и разогну, то получится прямая. Тогда я смогу померить её длину. А можно и не разрезать. Возьмите сантиметровую ленту у бабушки или у мамы. Потом найдите чашку на кухне, отметьте точку (незаметно, чтобы потом смыть) и действуйте по схеме:
Есть ещё формула площади круга:
Тоже легко. В статье я уже не буду об этом писать. А вот видео, в нём я задачи разбираю для шестиклассников, именно на эту тему. Там про площадь круга рассказываю подробно. Для других классов тоже подойдёт, кто не понял, забыл или не успел)))
Подведём итог. Если вы будете знать наизусть определение диаметра и радиуса, если вы будете знать 2 формулы (а на самом деле одну!) длины окружности и одну формулу площади круга, то по этой теме у вас точно будет не ниже четвёрки, друзья мои школьники.
Если статья показалась вам полезной, поставьте, пожалуйста, оценку. Она поможет мне дальше помогать вам)))
Вот здесь кое-что про борьбу со списыванием с сайта ГДЗ
А вот здесь – как учить стихи
P. S.: Про число “ПИ” я ничего не говорила в этой статье. Но в видео я про него рассказываю. Это фантастическое, просто удивительное число!!!!! Но мне места не хватило, В другой раз…
Как посчитать длину окружности
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать длину окружности
Чтобы посчитать длину окружности (круга) просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор

Как посчитать длину окружности зная диаметр
Какая длина у окружности если
её диаметр ?
Ответ:
0
Какова длина окружности (С) если её диаметр d?
Формула
С = π⋅d, где π ≈ 3.14
Пример
Если диаметр круга равен 1 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная радиус
Какая длина у окружности если
её радиус ?
Ответ:
0
Какова длина окружности (С) если её радиус r?
Формула
С = 2⋅π⋅r, где π ≈ 3.14
Пример
Если радиус круга равен 0.5 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная её площадь
Какая длина у окружности если
её площадь ?
Ответ:
0
Какова длина окружности (С) если её площадь S?
Формула
С = 2π⋅√S/π, где π ≈ 3.14
Пример
Если площадь круга равна 6 см2, то его длина примерно равна 8.68 см.