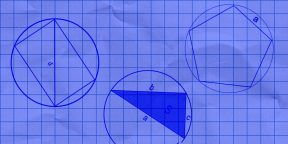
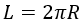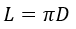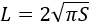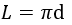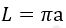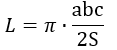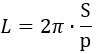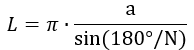8 способов найти длину окружности
Выбирайте формулу, ориентируясь на известные величины.
1. Как найти длину окружности через диаметр
Просто умножьте диаметр на число пи.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- d —диаметр окружности.
2. Как найти длину окружности через радиус
Умножьте число пи на два радиуса.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- r — радиус окружности.
3. Как вычислить длину окружности через площадь круга
Умножьте число пи на четыре площади круга.
Найдите корень из результата.
- O — искомая длина окружности.
- S – площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
4. Как найти длину окружности через диагональ вписанного прямоугольника
Умножьте число пи на диагональ.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- d – любая диагональ прямоугольника.
5. Как вычислить длину окружности через сторону описанного квадрата
Умножьте число пи на сторону квадрата.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- a – любая сторона квадрата.
6. Как найти длину окружности через стороны и площадь вписанного треугольника
Перемножьте стороны треугольника.
Поделите результат на площадь и на два.
Умножьте полученное число на пи.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- S – площадь треугольника.
- a, b, c – стороны треугольника.
7. Как найти длину окружности через площадь и полупериметр описанного треугольника
Поделите площадь треугольника на его полупериметр.
Умножьте результат на число пи и на два.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- S – площадь треугольника.
- p – полупериметр треугольника (равен половине от суммы всех сторон).
8. Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разделите 180 градусов на количество сторон многоугольника.
Найдите синус полученного числа.
Разделите сторону многоугольника на результат.
Умножьте получившееся число на пи.
- O — искомая длина окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- π (пи) — константа, равная 3,14.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✏️🎓
- Как найти периметр прямоугольника
- 8 способов найти периметр треугольника
- 7 способов найти площадь прямоугольника
- Как перевести обычную дробь в десятичную
- Как освоить устный счёт школьникам и взрослым
Длина (периметр) окружности калькулятор онлайн умеет вычислять длину восемью способами:
- По радиусу.
- По диаметру.
- По площади окружности.
- По диагонали вписанного прямоугольника.
- По стороне описанного квадрата.
- По сторонам и площади описанного треугольника.
- По площади вписанного треугольника.
- По стороне вписанного многогранника.
Сделав расчет периметра на этом онлайн калькуляторе Вы получите не только ответ, но и детальное, пошаговое решение с выводом формул и промежуточных действий.
Длина окружности или периметр окружности – это длина кривой из множества точек которая ограничивает собой круг.
Длина окружности может быть найдена по длине пути, который проедет круг сделав один полный оборот.
Как найти длину окружности?
Найти длину окружности очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
1) По радиусу
где R – радиус окружности.
2) По диаметру
где D – диаметр окружности.
3) По площади окружности
ггде S – площадь окружности.
4) По диагонали вписанного прямоугольника
где d – диагональ вписанного прямоугольника.
5) По стороне описанного квадрата
где a – сторона описанного квадрата.
6) По сторонам и площади описанного треугольника
где a,b,c – стороны описанного треугольника, S – его площадь.
7) По площади вписанного треугольника
где p – полупериметр вписанного треугольника, S – его площадь.
8) По стороне вписанного многогранника
где a – сторона вписанного многогранника, N – количество сторон.
Скачать все формулы в формате Word
Как посчитать длину окружности
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать длину окружности
Чтобы посчитать длину окружности (круга) просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор

Как посчитать длину окружности зная диаметр
Какая длина у окружности если
её диаметр ?
Ответ:
0
Какова длина окружности (С) если её диаметр d?
Формула
С = π⋅d, где π ≈ 3.14
Пример
Если диаметр круга равен 1 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная радиус
Какая длина у окружности если
её радиус ?
Ответ:
0
Какова длина окружности (С) если её радиус r?
Формула
С = 2⋅π⋅r, где π ≈ 3.14
Пример
Если радиус круга равен 0.5 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная её площадь
Какая длина у окружности если
её площадь ?
Ответ:
0
Какова длина окружности (С) если её площадь S?
Формула
С = 2π⋅√S/π, где π ≈ 3.14
Пример
Если площадь круга равна 6 см2, то его длина примерно равна 8.68 см.
См. также
Содержание материала
- Как найти длину отрезка (расстояние между точками) с помощью онлайн-калькулятора
- Видео
- Как найти длину окружности через стороны и площадь вписанного треугольника
- Свойства и линии
- Как вычислить длину окружности через сторону вписанного правильного многоугольника
- Как найти длину окружности
- Разбор примера
- Разбор примера
- Хорда и дуга окружности
Как найти длину отрезка (расстояние между точками) с помощью онлайн-калькулятора
Рассмотрим пример, наглядно демонстрирующий работу с онлайн-калькулятором. Найдем длину произвольного отрезка, начальная и конечная точки которого имеют координаты (1;4) и (3;0). Для этого:
- Выберем размерность (2 или 3). Калькулятор позволяет задать отрезок соответственно на плоскости, или в пространстве. В нашем конкретном примере выберем плоскость (2):
- Введем в пустые поля координаты начальной и конечной точек отрезка:
- После ввода координат остается нажать «Рассчитать» и получить ответ с решением:
Видео
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
где:
π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Свойства и линии
Из-за того, что прямоугольник — это параллелограмм, все свойства последнего справедливы и к нему. В первую очередь для него характерно, что противоположные стороны являются параллельными, то есть лежат на непересекающихся прямых. Отсюда следует, что фигуры отличаются друг от друга только размерами двух граней.
К основным свойствам прямоугольника относят:
- противолежащие стороны имеют равную длину: AB = CD, BC = AD;
- все углы равны 90 градусов;
- отрезки, обозначающие ширину и длину, всегда перпендикулярные друг другу: AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB;
- сумма любых двух углов фигуры равняется 180 градусов, соответственно всех четырёх — 360;
- в четырёхугольном теле можно провести 2 диагонали, длины которых будут совпадать по величине: AB = BC;
- сумма квадратов диагональных отрезков равняется удвоенной сумме квадратов сторон фигуры: AC2 + BD2 = 2 (AB2 + BC2);
- построенная диагональ разделяет прямоугольник на 2 одинаковые фигуры — прямоугольные треугольники;
- точка пересечения прямых линий, соединяющая попарно противоположные углы, является центром фигуры и описанной окружности;
- диагонали в месте пересечения разделяются на 4 равных отрезка;
- в многоугольник, у которого длина не равна ширине, вписать окружность нельзя, поэтому её можно построить только для частных случаев прямоугольника.
На свойстве, что сложенные квадраты диагоналей можно найти как сумму квадратов всех его сторон, построено решение многих геометрических задач. Нелишним будет доказательство теоремы. Пусть имеется прямоугольник, у которого линии AC и BD — диагонали. Если изобразить многоугольник на рисунке и построить отрезки, можно увидеть, что каждая диагональ делит фигуру на 2 треугольника: ABC и BDC.
Используя теорему косинусов, можно записать: AC2 = AB2 + BC2 — 2 * AB * BC * cos (ABC); BD2 = CD2 + BC2 — 2 * CD * BC * cos (BCD). После сложения полученных выражений получится запись: AC2 + BD2 = AB2 + BC2 — 2 * AB * BC * cos (ABC) + CD2 + BC2 — 2 * CD * BC * cos (BCD).
Так как по свойству прямоугольной фигуры противоположные стороны равны, уравнение примет вид: AC2 + BD2 = 2AB2 + 2BC2 — 2 * AB * BC * cos (ABC) — 2 * AB * BC * cos (BCD). Учитывая, что сумма двух углов равняется 180, полученное выражение можно переписать так: AC2 + BD 2 = 2 (AB 2 + BC 2). Что и следовало доказать.
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата. Формула вычисления длины окружности:
где:
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Разбор примера
Условие задачи:
Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.
Воспользуемся формулой длины окружности: C = 2πR ≈ 2 · 3,14 · 24 ≈ 150,72 см
Разберем обратную задачу, когда мы знаем длину окружности, а нас просят найти её диаметр.
Разбор примера
Условие задачи:
Определите диаметр окружности, если её длина равна 56,52 дм. (π ≈ 3,14).
Выразим из формулы длины окружности диаметр.
C = πD D = С / π D = 56,52 / 3,14 = 18 дм
Хорда и дуга окружности
На рисунке ниже отметим на окружности две точки «A» и «B». Эти точки делят окружность на две части, каждую из которых называют дугой. Это синяя дуга «AB» и черная дуга «AB». Точки «A» и «B» называют концами дуг.
Соединим точки «A» и «B» отрезком. Полученный отрезок называют хордой.

Точки «A» и «B» делят окружность на две дуги. Поэтому важно понимать, какую дугу вы имеете в виду, когда пишите дуга «AB». Для того чтобы избежать путаницы, часто вводят дополнительную точку на нужной дуге и обращаются к ней по трем точкам.

Теги
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Что такое окружность?
Окружность – это замкнутая плоская кривая, ограничивающая круг.
Или, другими словами, окружность представляет собой множество точек, удаленных на одно и тоже расстояние от центра круга на длину радиуса этого круга. А длина окружности – это длина этой кривой, которую образует это множество точек и которая ограничивает собой круг. Это хорошо видно на иллюстрации выше.
Как найти длину окружности?
Чтобы вычислить длину окружности, нужно знать радиус, диаметр или площадь круга. Причём достаточно только чего-то одного из этих элементов.
По диаметру
Диаметр — это такой отрезок, который соединяет две точки на окружности и проходит через центр круга. Чтобы найти длину окружности через диаметр, просто умножаем диаметр окружности на число Пи и получаем длину окружности.
Формула будет такой:
L = π × d
Где L – длина окружности, π – константа, равная примерно 3,14, а d – это диаметр.
Например, нам нужно посчитать периметр канализационной трубы диаметром 100 мм. Окружность этой трубы можно найти весьма несложными расчётами:
L = 3,14 × 100 = 314 мм.
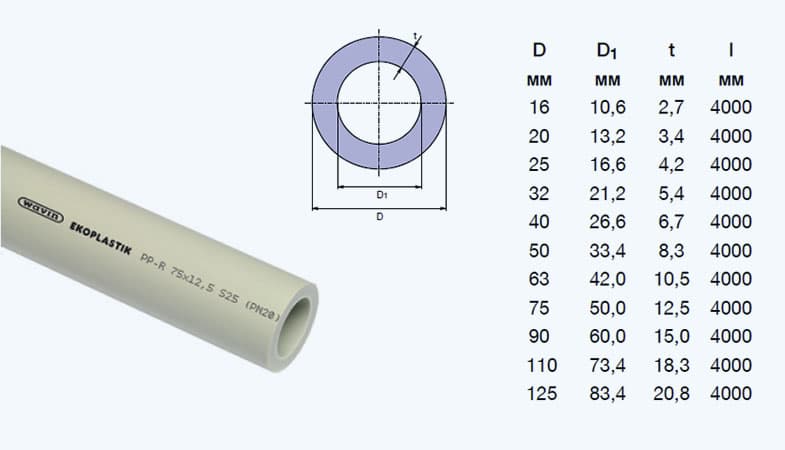
Кстати, у труб есть 2 окружности и 2 диметра: внутренние и внешние. Это хорошо показано на рисунке ниже.
Всегда обращайте внимание, какой именно диаметр известен и какую длину окружности вам требуется вычислить. Часто внутренний диаметр обозначается малой d или D1, а наружный просто – D или DN.
Зная радиус
Радиус окружности — это отрезок, который соединяет центр окружности с точкой на окружности. Радиус равен половине диаметра, поэтому вычисление длины окружности будет похоже на предыдущий случай: умножаем радиус на два и на число пи и получаем длину окружности.
Формула расчёта выглядит следующим образом:
L = 2π × R
Где L – длина окружности, π – константа (приблизительно 3,14), а r – это радиус.
К примеру, нужно посчитать длину внутренней окружности трубы, с внутренним радиусом 26 мм. В этом случае периметр получается следующим образом:
L = 2 × 3,14 × 26 = 163,28 мм.
Также обратите внимание, что в число Пи взято с точностью до двух знаков после запятой, и всегда расчёт через Пи идёт с округлением и является приблизительным.
Через площадь круга
И, пожалуй, самым редким случаем калькуляции периметра круга будет тот, когда нам известна только площадь этого круга. В этом случае, чтобы рассчитать длину окружности, можно воспользоваться следующей формулой:
L = (4Sπ)1/2
Где L – длина окружности, S – площадь круга, а π – константа, равная 3,14.
То есть длина окружности равна квадратному корню произведения площади круга, числу пи, умноженному на четыре. На всякий случай, корень и степень ½ – это одно и то же.
Возьмём пример, к нам прилетели инопланетяне и оставили круги на полях.
Площадь одного из этих кругов составила аж 1146,5 квадратных метра. Чтобы рассчитать длину окружности, нужно сделать следующее:
- Умножить 4 на 3,14, и полученное произведение умножить на площадь круга 1146,5. Получаем 14400,04.
- И теперь находим квадратный корень из этого числа и получаем примерно 120 метров. Это и есть длина окружности.
Как и в прошлых случаях из-за наличия числа Пи, которое является иррациональным, ответ будет считаться с округлением.
❓Вопросы и ответы
И наконец, предлагаем вам прочитать ответы на некоторые часто задаваемые вопросы относительно вычисления длины окружности.
Что что имеет большее значение радиус, диаметр, длина окружности или площадь круга?
Площадь круга. А если выставить всё это по мере убывания, то рейтинг будет таким:
- Площадь круга
- Длина окружности
- Диаметр
- Радиус
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разные калькуляторы, в частности калькуляторы: диаметра, площади круга и длины окружности. Для последней калькулятор находится наверху данной страницы.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Хватит ли чего-то одного (диаметра, радиуса, площади) для расчёта длины окружности?
Да, хватит. Формулы и примеры расчетов периметра круга, в которых используется что-то одно из перечисленного, есть выше на данной странице.
Что такое внутренняя и внешняя окружность? Чем они отличаются?
Внутренняя и внешняя окружность (а также диаметр) чаще всего используются для расчёта параметров труб, у которых есть стенки ненулевой ширины. Поэтому окружность внутри трубы всегда меньше окружности снаружи. Для окружности снаружи используется обозначение L или LN, а диаметра – D или DN. А для периметра и диаметра круга внутри добавляется нижний индекс «единица»: L1 и D1, или используются буквы в нижнем регистре (малые): l и d.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии