Загрузить PDF
Загрузить PDF
Многие характеристики графика функции или многочлена невозможно объяснить без визуального представления. Одна из таких характеристик — ось симметрии: вертикальная линия на графике, которая делит этот график на два зеркально симметричных изображения. Найти ось симметрии для данного многочлена относительно несложно.[1]
Существует два основных способа.
-

1
Определите, какова степень многочлена. Степень многочлена — это наибольшая степень, которую имеют одночлены в этом выражении.[2]
Если степень данного многочлена равна 2 (ни один одночлен в выражении не имеет степени выше, чем x2), вы можете найти ось симметрии, используя данный способ. Если степень многочлена больше двух, применяйте второй способ.- Чтобы наглядно продемонстрировать этот способ, возьмем, например, многочлен вида 2x2 + 3x – 1. Самая высокая степень в многочлене — x2, следовательно, мы имеем дело с квадратным трехчленом и можем воспользоваться первым способом для нахождения оси симметрии.
-

2
Подставьте коэффициенты в формулу расчета оси симметрии. Для нахождения оси симметрии для квадратного трехчлена вида ax2 + bx +c (парабола), применяют базовую формулу x = -b / 2a.[3]
- В нашем примере a = 2, b = 3, and c = -1. Подставим эти значения в нашу формулу, и получаем:
x = -3 / 2(2) = -3/4.
- В нашем примере a = 2, b = 3, and c = -1. Подставим эти значения в нашу формулу, и получаем:
-

3
Запишите уравнение оси симметрии. Значение, которое вы рассчитали по формуле оси симметрии, — это значение точки пересечения оси симметрии с осью абсцисс.
- В вышеприведенном примере ось симметрии равна -3/4.
Реклама
-

1
Определите степень многочлена. Степень многочлена — это наибольшая степень, которую имеют одночлены в этом выражении. Если степень данного многочлена равна 2 (ни один одночлен в выражении не имеет степени выше, чем x2), вы можете найти ось симметрии, используя вышеприведенный способ. Если степень многочлена больше 2, применяйте графический способ.
-

2
Начертите систему координат. Нарисуйте две линии, пересекающиеся под прямым углом в виде знака «плюс». Горизонтальная линия будет осью x, а вертикальная — осью у.
-

3
Отложите единичные числовые отрезки на осях. Отложите на осях числовые отрезки равной величины.
-

4
Рассчитайте значение y = f(x) для каждого значения x. Возьмите данный многочлен или функцию и рассчитайте значения f(x), последовательно подставив в выражение значения x.
-

5
Отметьте точки на графике для каждой пары координат. Теперь у вас есть соответствующее значение y = f(x) для каждого значения на оси абсцисс. Для каждой точки с координатами (x, y), отметьте точку в системе координат — по вертикали отложив значение по оси X, а по горизонтали — на оси Y.
-

6
Нарисуйте график многочлена. Когда вы нанесли все точки на систему координат, можно плавно соединить их между собой. У вас получится непрерывный график вашего многочлена.
-

7
Найдите ось симметрии. Внимательно изучите полученный график. Найдите точку на графике, по которой можно провести линию, разделяющую график на две равные зеркальные половины.[4]
-

8
Отметьте ось симметрии. Если вы нашли такую точку (назовем ее «b») на оси x, которая разделяет график на две зеркальные половины, это значение и будет искомой осью симметрии.
Реклама
Советы
- Длина осей абсцисс и ординат должна быть достаточной, чтобы наглядно отобразить форму графика.
- Некоторые многочлены не имеют оси симметрии. Например, для y = 3x не существует оси симметрии.
- Симметрия многочлена может быть определена как четная или нечетная. Любой график, ось симметрии которого совпадает с осью у имеет «четную» симметрию. Любой график, ось симметрии которого совпадает с осью x, — «нечетный».
Реклама
Об этой статье
Эту страницу просматривали 111 502 раза.
Была ли эта статья полезной?
Кривые второго порядка. Эллипс: формулы и задачи
Понятие о кривых второго порядка
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:
,
где A, B, C, D, E, F – числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Эллипс, заданный каноническим уравнением
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как и на рисунке ниже.
Каноническое уравнение эллипса имеет вид:
,
где a и b (a > b) – длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.
Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат – в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат – малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b , то уравнение эллипса принимает вид . Это уравнение окружности радиуса a , а окружность – частный случай эллипса. Эллипс можно получить из окружности радиуса a , если сжать её в a/b раз вдоль оси Oy .
Пример 1. Проверить, является ли линия, заданная общим уравнением , эллипсом.
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия – эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось – это a = 5 , меньшая полуось – это b = 4 . Получаем каноническое уравнение эллипса:
.
Точки и , обозначенные зелёным на большей оси, где
,
называются фокусами.
называется эксцентриситетом эллипса.
Отношение b/a характеризует “сплюснутость” эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
– если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,
– если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат – каноническое уравнение эллипса:
.
Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет .
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:
.
Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением .
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:
.
Получаем фокусы эллипса:
Решить задачи на эллипс самостоятельно, а затем посмотреть решение
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) расстояние между фокусами 30, а большая ось 34
2) малая ось 24, а один из фокусов находится в точке (-5; 0)
3) эксцентриситет , а один из фокусов находится в точке (6; 0)
Продолжаем решать задачи на эллипс вместе
Если – произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и – расстояния до этой точки от фокусов , то формулы для расстояний – следующие:
.
Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями
,
называются директрисами эллипса (на чертеже – красные линии по краям).
Из двух вышеприведённых уравнений следует, что для любой точки эллипса
,
где и – расстояния этой точки до директрис и .
Пример 7. Дан эллипс . Составить уравнение его директрис.
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. . Все данные для этого есть. Вычисляем:
.
Получаем уравнение директрис эллипса:
Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки , а директрисами являются прямые .
Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:
.
Теперь можем получить и квадрат длины меньшей полуоси:
Уравнение эллипса готово:
Пример 9. Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса.
Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:
.
Получили единицу, следовательно, точка находится на эллипсе.
Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e – эксцентриситет и числа “эр” с подстрочными индексами 1 и 2 – искомые расстояния. Получаем:
Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.
,
так как из исходного уравнения эллипса .
Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
Эллипс – определение и вычисление с примерами решения
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно Согласно определению эллипса имеем Из треугольников и по теореме Пифагора найдем
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим Раскроем разность квадратов Подставим найденное выражение в уравнение и сократим обе части равенства на 4, тогда оно перейдет в уравнение Вновь возведем обе части равенства в квадрат Раскрывая все скобки в правой части уравнения, получим Соберем не- известные в левой части, а все известные величины перенесем в правую часть уравнения, получим Введем обозначение для разности, стоящей в скобках Уравнение принимает вид Разделив все члены уравнения на получаем каноническое уравнение эллипса: Если то эллипс вытянут вдоль оси Ох, для противоположного неравенства – вдоль оси Оу (при этом фокусы тоже расположены на этой оси). Проанализируем полученное уравнение. Если точка М(х; у) принадлежит эллипсу, то ему принадлежат и точки следовательно, эллипс симметричен относительно координатных осей, которые в данном случае будут называться осями симметрии эллипса. Найдем координаты точек пересечения эллипса с декартовыми осями:
- т.е. точками пересечения эллипса с осью абсцисс будут точки
- т.е. точками пересечения эллипса с осью ординат будут точки (Рис. 30).
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если то параметр а называется большой, а параметр b – малой полуосями эллипса.
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству Кроме того, эта характеристика описывает форму эллипса. Для демонстрации этого факта рассмотрим квадрат отношения малой полуоси эллипса к большой полуоси
Если и эллипс вырождается в окружность. Если и эллипс вырождается в отрезок
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр Зная параметр с, можно вычислить малую полуось эллипса Следовательно, каноническое уравнение заданного эллипса имеет вид:
Пример:
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса а третья вершина – в центре окружности
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
Следовательно, большая полуось эллипса а малая полуось Так как то эллипс вытянут вдоль оси ординат Оу. Определим расположение фокусов данного эллипса Итак, Окружность: Выделим полные квадраты по переменным Следовательно, центр окружности находится в точке О(-5; 1).
Построим в декартовой системе координат треугольник Согласно школьной формуле площадь треугольника равна Высота а основание Следовательно, площадь треугольника равна:
Эллипс в высшей математике
где и —заданные положительные числа. Решая его относительно , получим:
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное по абсолютной величине меньше , подкоренное выражение положительно, корень имеет два значения. Каждому значению , удовлетворяющему неравенству соответствуют два значения , равных по абсолютной величине. Значит, геометрическое место точек, определяемое уравнением (2), симметрично относительно оси . Так же можно убедиться в том, что оно симметрично и относительно оси . Поэтому ограничимся рассмотрением только первой четверти.
При , при . Кроме того, заметим, что если увеличивается, то разность уменьшается; стало быть, точка будет перемещаться от точки вправо вниз и попадет в точку . Из соображений симметрии изучаемое геометрическое место точек будет иметь вид, изображенный на рис. 34.
Полученная линия называется эллипсом. Число является длиной отрезка , число —длиной отрезка . Числа и называются полуосями эллипса. Число эксцентриситетом.
Пример:
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом (рис. 35). В каждой из этих плоскостей возьмем систему координат, причем за ось примем прямую пересечения плоскостей, стало быть, ось будет общей для обеих систем. Оси ординат различны, начало координат общее для обеих систем. В плоскости возьмем окружность радиуса с центром в начале координат, ее уравнение .
Пусть точка лежит на этой окружности, тогда ее координаты удовлетворяют уравнению .
Обозначим проекцию точки на плоскость буквой , а координаты ее—через и . Опустим перпендикуляры из и на ось , это будут отрезки и . Треугольник прямоугольный, в нем , ,, следовательно, . Абсциссы точек и равны, т. е. . Подставим в уравнение значение , тогда cos
а это есть уравнение эллипса с полуосями и .
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей с коэффициентами деформации, равными
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам (х, у, z) с текущими координатами х, у, г, причем
Иными словами, линейные размеры сферы в направлении оси Ох уменьшаются в раз, если , и увеличиваются в раз, если и т. д.
Подставляя эти формулы в уравнение (1), будем иметь
где Уравнение (2) связывает текущие координаты точки М’ эллипсоида и, следовательно, является уравнением трехосного эллипсоида.
Величины называются полуосями эллипсоида; удвоенные величины называются осями эллипсоида и, очевидно, представляют линейные размеры его в направлениях деформации (в данном случае в направлениях осей координат).
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Как найти координаты фокусов эллипса
Понятие о кривых второго порядка
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:
,
где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Эллипс, заданный каноническим уравнением
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как и на рисунке ниже.
Каноническое уравнение эллипса имеет вид:
,
где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.
Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат — в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат — малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b , то уравнение эллипса принимает вид . Это уравнение окружности радиуса a , а окружность — частный случай эллипса. Эллипс можно получить из окружности радиуса a , если сжать её в a/b раз вдоль оси Oy .
Пример 1. Проверить, является ли линия, заданная общим уравнением , эллипсом.
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5 , меньшая полуось — это b = 4 . Получаем каноническое уравнение эллипса:
.
Точки и , обозначенные зелёным на большей оси, где
,
называются фокусами.
называется эксцентриситетом эллипса.
Отношение b/a характеризует “сплюснутость” эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,
— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат — каноническое уравнение эллипса:
.
Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет .
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:
.
Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением .
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:
.
Получаем фокусы эллипса:
Решить задачи на эллипс самостоятельно, а затем посмотреть решение
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) расстояние между фокусами 30, а большая ось 34
2) малая ось 24, а один из фокусов находится в точке (-5; 0)
3) эксцентриситет , а один из фокусов находится в точке (6; 0)
Продолжаем решать задачи на эллипс вместе
Если — произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:
.
Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями
,
называются директрисами эллипса (на чертеже — красные линии по краям).
Из двух вышеприведённых уравнений следует, что для любой точки эллипса
,
где и — расстояния этой точки до директрис и .
Пример 7. Дан эллипс . Составить уравнение его директрис.
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. . Все данные для этого есть. Вычисляем:
.
Получаем уравнение директрис эллипса:
Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки , а директрисами являются прямые .
Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:
.
Теперь можем получить и квадрат длины меньшей полуоси:
Уравнение эллипса готово:
Пример 9. Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса.
Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:
.
Получили единицу, следовательно, точка находится на эллипсе.
Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа “эр” с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:
Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.
,
так как из исходного уравнения эллипса .
Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
1. Окружность. 2Окружностью называется геометрическое место точек, равноудаленных от одной фиксированной точки, называемой центром окружности. Расстояние от произвольной точки окружности до его центра называется радиусом окружности.
g Если центр окружности находится в точке , а радиус равен R, то уравнение окружности имеет вид:
. (3.13)
4Обозначим через (рис. 3.5) произвольную точку окружности. Используя формулу расстояния между двумя токами (3.1) и определение окружности, получим: . Возводя полученное равенство в квадрат, мы получим формулу (3.13).3
2. Эллипс. 2 Эллипсом называется геометрическое место точек, сумма расстояний которых до двух фиксированных точек, называемых фокусами, есть величина постоянная.
Для того, чтобы вывести каноническое (простейшее) уравнение эллипса, примем за ось Ox прямую, соединяющую фокусы F1 и F2. Пусть при этом фокусы будут симметричны относительно начала координат, т.е. будут иметь координаты: и . Здесь через 2с обозначено расстояние между фокусами. Обозначим через x и y координаты произвольной точки М эллипса (рис 3.6). Тогда по определению эллипса, сумма расстояний от точки М до точек F1 и F2 равно константе (обозначим эту константу через 2а).
. (3.14)
Уравнение (3.14) является уравнением эллипса. Упростим данное уравнение, избавившись от квадратных корней. Для этого перенесем один из радикалов в правую часть равенства (3.14) и возведем обе части полученного равенства в квадрат:
,
,
,
.
Возводя последнее равенство в квадрат, получим
, или
,
.
Разделим обе части на :
.
Так как сумма расстояний от произвольной точки эллипса до его фокусов больше расстояния между фокусами, т.е. 2а > 2c, то .
Обозначим через b 2 . Тогда простейшее (каноническое) уравнение эллипса будет иметь вид:
, (3.15)
. (3.16)
Оси координат являются осями симметрии эллипса, заданного уравнением (3.15). Действительно, если точка с текущими координатами (x; y) принадлежит эллипсу, то и точки при любом сочетании знаков принадлежат эллипсу.
2Ось симметрии эллипса, на которой расположены фокусы, называется фокальной осью. Точки пересечения эллипса с его осями симметрии называются вершинами эллипса. Подставляя x = 0 или y = 0 в уравнение эллипса найдем координаты вершин:
2Отрезки А1А2 и B1B2, соединяющие противоположные вершины эллипса, а также их длины 2a и 2b, называют соответственно большой и малой осями эллипса. Числа a и b, называют соответственно большой и малой полуосями эллипса.
2Эксцентриситетом эллипса называется отношение расстояния между фокусами (2с) к большой оси (2a), т.е.
. (3.17)
Так как а и с положительны, причем c
2Отрезок 2a, длина которого равна расстоянию между вершинами гиперболы, называют действительной осью гиперболы. Отрезок 2b называют мнимой осью гиперболы. Числа a и b, называют соответственно действительной и мнимой полуосями гиперболы.
Можно доказать, что прямые линии
(3.23)
являются асимптотами гиперболы, т.е. такими прямыми, к которым неограниченно приближаются точки гиперболы при их неограниченном удалении от начала координат ( ).
2Эксцентриситетом гиперболы называется отношение расстояния между фокусами (2с) к действительной оси (2a), т.е., как и в случае эллипса
. (3.24)
Однако в отличии от эллипса эксцентриситет гиперболы больше единицы.
Если фокусы гиперболы расположены на оси Oy, то в левой части уравнения гиперболы изменятся знаки на противоположные:
. (3.25)
В этом случае полуось b будет действительной, а полуось a – мнимой. Ветви гиперболы будут симметричны относительно оси Oy (рис 3.9). Формулы (3.22) и (3.23) не изменятся, формула (3.24) будет выглядеть следующим образом:
. (3.26)
4. Парабола. Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой фокусом и от данной прямой, называемой директрисой (предполагается, что фокус не лежит на директрисе).
Для того, чтобы составить простейшее уравнение параболы примем за ось Ox прямую, проходящую через ее фокус перпендикулярно директрисе, и направленную от директрисы к фокусу. За начало координат примем середину отрезка O от фокуса F до точки А пересечения оси Ox с директрисой. Длина отрезка AF обозначается через p и называется параметром параболы.
В данной системе координат координаты точек А и F будут, соответственно, , . Уравнение директрисы параболы будет . Обозначим через (x; y) координаты произвольной точки М параболы (рис. 3.10). Тогда по определению параболы:
. (3.27)
Возведем обе части равенства (3.27) в квадрат:
, или
, откуда
. (3.28)
Уравнение (3.28) называется каноническим уравнением параболы.
Каноническими являются так же следующие уравнения параболы.
. (3.29)
Ветви параболы, заданной уравнением (3.29), направлены влево, фокус имеет координаты , уравнение директрисы .
. (3.30)
Ветви параболы, заданной уравнением (3.30), направлены вверх, фокус имеет координаты , уравнение директрисы .
. (3.31)
Ветви параболы, заданной уравнением (3.31), направлены вниз, фокус имеет координаты , уравнение директрисы .
Задача 3.3. Найти координаты фокусов и эксцентриситет эллипса:
Решение. В каноническом виде уравнение эллипса выглядит следующим образом: Из этого уравнения видно, что большая полуось эллипса равна а малая полуось равна Расстояние от центра эллипса до его фокусов, находим из формулы (3.16): Таким образом, фокусы эллипса имеют координаты:
Эксцентриситет эллипса найдем по формуле (3.17):
Задача 3.4. Асимптоты гиперболы имеют уравнения и расстояние между фокусами равно 10. Составить каноническое уравнение гиперболы.
Решение. Из условия задачи следует, что
.
Подставляя в равенство (3.22) с = 5 и a = 2b, мы получим уравнение, из которого найдем b:
b 2 = 25 – 4b 2 , 5b 2 = 25, b 2 = 5, . Следовательно, a = 2b = .
Подставляя a 2 = 20 и b 2 = 5 в уравнение (3.21), получим искомое уравнение гиперболы:
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент — человек, постоянно откладывающий неизбежность. 10572 — | 7332 — или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Эллипс – геометрическое место точек M(x;y), сумма расстояний которых до двух данных точек F1F2 имеет одно и то же значение 2a:
точки F1 и F2 – называются фокусами эллипса;
расстояние F1F2 – фокусное расстояние и равно F1F2=2с;
a — большая полуось;
b — малая полуось;
c — фокальный радиус, то есть полу расстояние между фокусами;
p — фокальный параметр;
Rmin – минимальное расстояние от фокуса до точки на эллипсе;
Rmax — максимальное расстояние от фокуса до точки на эллипсе;
где
Длина малой оси эллипса 134 м. Длина большой оси равна 140 м. Найти коэффициент сжатия k и сжатие α этого эллипса
Постройте кривую 4x 2 +9y 2 =36. Найдите фокусы, фокальный параметр и эксцентриситет.
Делим обе части на 36 и получаем каноническое уравнение эллипса
a=3, b=2
c 2 =a 2 -b 2 =3 2 -2 2 =9-4=5
Отсюда находим Фокусы F1(-2,2;0) F2(2,2;0)
Фокальный параметр находим следующим образом
Эксцентриситет эллипса
Пример 3
Постройте кривую . Найдите фокусы и эксцентриситет.
Решение
Уравнение запишем в виде
a=1, b=5
Это уравнение не является каноническим уравнением эллипса, так как b>a, а должно быть b c 2 =a 2 − b 2 =5 2 −1 2 =25 − 1=24
Следовательно, фокусы в системе координат (x’;y’) имеют координаты (-4,9;0) и (4,9;0), а в системе (x;y) координаты
Эксцентриситет эллипса равен
[spoiler title=”источники:”]
http://www.evkova.org/ellips
http://hd01.ru/info/kak-najti-koordinaty-fokusov-jellipsa/
[/spoiler]
Вычисление длины плоской кривой. Основные формулы
Если плоская кривая
задана как график функции y
= f(x),
a
≤ x
≤ b,
и производная y
= f
(x)
непрерывна, то длина дуги этой кривой
выражается интегралом
l
=
![]()
=
![]()
.
Если кривая задана
параметрически x
= x(t),
y
= y(t),
≤ t
≤
и производные x
(t)
и y
(t)
непрерывны на отрезке [,
],
то длина дуги кривой выражается интегралом
l
=![]()
.
Если кривая задана
уравнением r
=
r(),
≤
≤ ,
в полярных координатах и r
()
непрерывна на отрезке [,
],
то длина l
дуги кривой выражается интегралом
l
=
![]()
.
Если
Г –
пространственная
кривая, заданная параметрически: x
= x(t),
y
= y(t),
z
= z(t),
≤ t
≤ ,
производные x
(t),
y
(t)
и z
(t)
непрерывны на отрезке [,
],
то длина Г
находится
по формуле
l
=
![]()
.
Замечание.
Пусть Г – некоторая кривая на плоскости
xOy.
Выражение
dl
=
![]()
,
где dx2
= (dx)2,
dy2
= (dy)2,
называется дифференциалом длины дуги.
Используя это понятие, можно единообразно
записать формулу для вычисления длины
кривой
l
=
![]()
=
![]()
,
где
и ,
≤ ,
обозначают границы изменения параметра,
с помощью которого задается кривая.
Пусть кривая Г есть график функции
x
= x(y),
c
≤ y
≤ d.
Тогда dx
=
x
(y)
dy
и мы получаем
l
=![]()
=
![]()
.
Если кривая Г
задана параметрически, то dx
=
x
(t)
dt,
dy
=
y
(t)
dt
и мы получаем
l
=
=
![]()
=
![]()
.
Задание кривой с
помощью полярных координат r
= r(),
≤ ≤
,
есть частный случай параметрического
задания: x
= r()cos
,
y
=
= r()
sin
.
Параметром здесь является .
Вычисляя дифференциалы dx
= (r cos –
r sin )
d,
dy
= (r sin
+ r
cos ) d,
убеждаемся, что
dl
=
=![]()
.
Для пространственной
кривой Г
дифференциалом
длины дуги называется выражение l
=![]()
и длину кривой
Г
можно выразить
интегралом
l
=
=
![]()
,
где
и
(
≤ ) –
концы отрезка [,
] –
промежутка изменения параметра, с
помощью которого задается кривая.
Рассмотрим примеры.
Вычислить
длину дуги кривой.
5.19.
y
=
1 – ln cos
x,
0 ≤
x ≤
![]()
.
5.20.
y
=
2![]()
,
0 ≤
x ≤
1.
5.21.
x
=
![]()
,
0 ≤
y ≤
4.
5.22.
3y2
=
x(x
– 1)2
(длину петли).
5.23.
y =
![]()
,
0 ≤
x ≤
ln 4.
5.24.
y
=![]()
,
0 ≤ x
≤
![]()
.
Решение.
5.19. Так как y
=![]()
=
tg
x,
то


.
5.20. Так как
![]()
,
то

![]()
.
Можно было
рассмотреть нашу кривую как график
функции
![]()
,
![]()
.
Тогда вычисление длины кривой свелось
бы к нахождению интеграла
![]()
.
5.21. Вычисляем
производную
![]()
=![]()
и далее
![]()
=

=

,
откуда

=

=
![]()
=
![]()
.
5.22. Из условия
следует, что y
= 0 при x
= 0 и x
= 1, причем
линия симметрична относительно оси Ox,
так как y
входит в уравнение в четной степени.
Ясно, что достаточно вычислить длину
половины петли, задаваемой уравнением
y
=![]()
,
![]()
.
(Вторая половина петли есть график
функции
![]()
).
Так как
![]()
,
![]()
= ![]()
,
то мы получаем
![]()
=

=
![]()
.
5.23.
Делаем предварительные вычисления:
![]()
=
![]()
–
![]()
=
![]()
.
Вычисляем длину
кривой
l
=
![]()
=
![]()
=
![]()
= 2.
5.24. Вычисляем
производную:
=

,
тогда
=
![]()
=
![]()
.
Вычисляем длину
кривой
l
=

=

=
![]()
=
=
![]()
=
![]()
=
![]()
=
=
![]()
.
Вычислить длину
кривой, заданной в полярных координатах.
5.25.
r
=
![]()
,
–![]()
≤
≤
.
5.26.
r
= a(1
+ cos
),
0 ≤
≤ 2π
(кардиоида).
5.27.
r
= th![]()
,
0 ≤
≤
2.
5.28.
r
= a cos4![]()
.
Решение.
5.25. Вычисляем длину
кривой по формуле
l
=

=

=

=
=
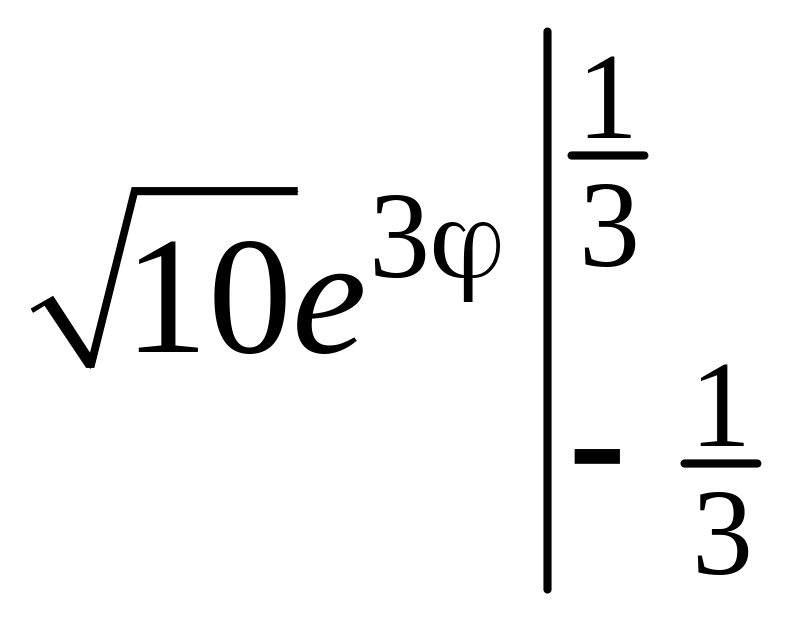
=
![]()
=
![]()
.
5.26.
l
=
![]()
=
![]()
=
=![]()
=
![]()
=
![]()
–![]()
=
= ![]()
–
![]()
= 4a + 4a
= 8a.
5.27.
l
=
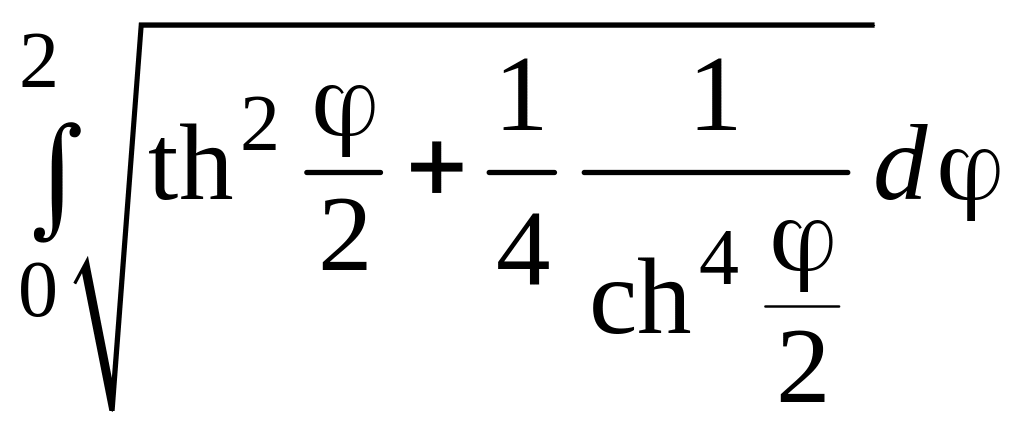
=

=
=

=

=

=
=

=

=
![]()
= 1 – th1.
5

Рис. 2.16
.28. Функция cos
имеет период 8π.
Функции
![]()
,
cos2
,
cos4
и т.п. имеют период 4π.
Поскольку
![]()
=
![]()
,
то линия симметрична относительно
полярной оси и при изменении
от 0 до 2π полярный радиус опишет половину
линии. Найдем длину половины кривой
(рис. 2.16) и затем удвоим результат.
Вычисляем
![]()
= a2![]()
+
![]()
=
![]()
.
Отсюда следует
l
=
![]()
=
![]()
=

=
= ![]()
=
![]()
.
Вычислить длину
кривой, заданной параметрически.
5.29.
x
= 6t5,
y
= 5t(1
– t8),
0 ≤
t
≤ 1.
5.30.
x
= ln(1 +
t2),
y
= 2arctg t –
2t
+
8, 0 ≤
t
≤ 1.
5.31.
x
= t
–
![]()
sh
2t,
y
= 2 ch t,
0 ≤
t
≤ 1.
5.32.
x
= 2 cos3
t,
y
= 2 sin3
t.
5.33.
x
=
t2,
y
= t
– t3
(длину петли).
Решение.
5.29. Вычисляем,
используя соответствующую формулу:
l
=
![]()
=
![]()
=
= 5![]()
= 5![]()
=
![]()
= 10.
5.30.
![]()
=
![]()
+
![]()
=
![]()
.
Поэтому
l
=
![]()
=
![]()
=
![]()
.
5.31.
= (1 – ch 2t)2
+ 4sh2t
= |
ch 2t –
1 = 2 sh2
t |
= 4 sh4 t
+ 4sh2 t
=
= 4 sh2
t
ch2 t
= sh2
2t.
Поэтому
l
=
![]()
=
![]()
=
![]()
= sh2 1.
5.32.
Уравнение линии (астроиды) в декартовых
координатах имеет вид

или
![]()
(рис. 2.17).
О

Рис.
2.17
тсюда следует, что линия симметрична
относительно обеих осей координат.
Вычислим четверть длины астроиды, что
соответствует изменению параметра t
от 0 до
,
и результат учетверим. Вычисляем
= 36 cos4
t
sin2 t
+ 36 sin4 t
cos2 t
=
= 36 sin2
t
cos2 t
= 9 sin2 2t.
Отсюда следует
l
=

=

= 6 + 6 = 12.
5.33. Если выразить
y
через x,
то мы получаем
![]()
,
откуда следует,
что при x
[0,
]
графики симметричных относительно оси
Ox
функций
![]()
и
![]()
образуют замкнутый
контур на плоскости xOy
(петлю). График функции
получается, когда
t
изменяется от –1 до 0, а при изменении t
от 0 до 1 точка (x,
y)
движется по графику функции
от точки O
(0, 0) до точки A(
,
0).
Вычисляем сначала
= 12t2
+ (1 – 3t2)2
= (1 + 3t2)2.
Поэтому
l
=
![]()
=
![]()
= 4.
Вычислить длину
дуги пространственной кривой.
5.34.
x
= 3t
– t3,
y
= 3t2,
z
= 3t
+
t3,
0 ≤ t
≤ 1.
5.35.
x
= at,
y
=
![]()
,
z
=
![]()
,
![]()
≤
t
≤ 1.
5.36.
x
= et,
y
= e-t,
z
=
t,
0 ≤
t
≤ 2.
5.37.
x
= a
(1 + cos
t),
y
=
a(t
– sin
t),
z
= 4
a sin![]()
,
0 ≤
t
≤ 2.
Решение.
5.34. Вычисляем длину
кривой по формуле
l
=
![]()
=
![]()
=
=
![]()
=
![]()
=
![]()
= 4
.
5.35.
![]()
=

=
= ![]()
=
![]()
=
![]()
.
Отсюда получаем
l
=

=

=
![]()
=
![]()
.
5.36. Имеем
![]()
=
e2t+
e–2t
+2
= (et
+
e–t)2.
Откуда
получаем
l
=
![]()
=
![]()
=![]()
= 2 sh
2.
5.37.
Сделаем предварительные вычисления:
= 4![]()
=
=
![]()
=
4a2.
Мы использовали
здесь тригонометрическую формулу 1 –
cos t
= = ![]()
.
Вычисляем длину
кривой
l
=
![]()
= 4a.
Вычисление
объемов и площадей поверхностей. Основные
формулы.
Пусть S(x) –
площадь сечения тела V
плоскостью, перпендикулярной к оси Ox
в точке с абсциссой x,
a
и b –
левая и правая границы изменения x.
Тогда объем тела V
выражается интегралом
V
=
![]()
.
Если тело V
образовано вращением вокруг оси Ox
криволинейной трапеции, ограниченной
кривой y
= f(x)
≥ 0, a
≤ x
≤ b,
осью абсцисс и прямыми x
= a,
x
= b,
то объем тела V
вычисляется по формуле
V
=
![]()
=
![]()
.
Если
тело образовано вращением вокруг оси
Oy
криволинейной трапеции, образованной
подграфиком функции x
= g(y),
c≤
y
≤ d
(g(y)
≥ 0), то
объем тела выражается интегралом
V
=
![]()
=
![]()
.
Если вокруг оси
Oy
вращается криволинейная трапеция,
ограниченная
графиком функции y
= f(x)
≥ 0, a
≤
x
≤
b,
осью абсцисс и прямыми x
=
a,
x
=
b,
то объем получившегося тела выражается
интегралом
V
=
![]()
=
![]()
.
Если кривая задана
параметрически или в полярных координатах,
то следует сделать соответствующую
замену переменных в указанных выше
формулах.
Площадь поверхности,
образованной вращением вокруг оси Ox
дуги Г кривой y
= f(x),
a
≤ x
≤ b,
где f(x)
имеет на отрезке [a,
b]
непрерывную производную
![]()
,
выражается интегралом
S
=
![]()
=
![]()
.
Поскольку
![]()
–
дифференциал длины дуги, то формулу
можно записать в виде
S
=![]()
.
Пусть кривая задана
параметрически x
= x(t),
y
= y(t),
≤ t
≤ ,
где функции
x(t)
и y(t)
имеют на отрезке [,
]
непрерывные производные x(t)
и y(t).
Площадь S
поверхности,
образованной при вращении данной кривой
вокруг оси Ox
равна
S
=![]()
=![]()
.
Задание кривой с
помощью полярных координат r
= r(),
≤
≤ ,
есть частный случай параметрического
задания, так как в этом случае
x
= r()
cos ,
y =
r()
sin .
Рассмотрим примеры.
5.38.
На всех хордах круга радиуса R,
параллельных одному направлению,
построены симметричные параболические
сегменты постоянной высоты h
(рис. 2.18).
Плоскости сегментов перпендикулярны
к плоскости круга. Найти объем образованного
таким образом тела.

а б
Рис. 2.18
Решение.
Найдем вначале площадь параболического
сегмента с основанием a
и высотой h
(рис. 2.18, б).
Расположим оси координат так, что
основание сегмента будет находиться
на оси абсцисс и начало координат делит
это основание пополам. Уравнение параболы
имеет вид
![]()
.
Так как y(0)
= h,
то
= –![]()
.
Тогда уравнение параболы принимает вид
![]()
.
Ищем площадь
сегмента
S
=
=

=

=
ah.
Расположим оси
координат так, как показано на рис. 2.18,
а.
Тогда длина половины хорды, пересекающей
ось абсцисс в точке x,
есть
![]()
.
Следовательно, площадь параболического
сегмента, соответствующего значению
x,
равна S(x)
=
![]()
.
Согласно формуле для объема, получаем
V
=![]()
=
![]()
=
![]()
=
=
=

=
![]()
.
5.39. Найти объем
тела, ограниченного поверхностями z
= 4 – y2,
x
= 0, x
= a,
y
= 0, z
= 0.
Р

Рис. 2.19
ешение. Найдем площадь
сечения тела плоскостью, перпендикулярной
к оси Ox,
(0 ≤ x
≤ a)
(рис. 2.19). Нам необходимо знать площадь
половины параболического сегмента с a
= 2, h
= 4. Как мы знаем из решения предыдущей
задачи, эта площадь равна
S(x)
=
![]()
=
![]()
,
0 ≤ x
≤ a.
Отсюда получаем
V
=
![]()
=
![]()
=
![]()
.
Найти объем тела,
образованного вращением фигуры,
ограниченной следующими линиями.
5.40.
y
= sin
x,
x
= 0, 0 ≤ x
≤ π, вокруг оси: а)
Ox,
б)
Oy.
5.41.
y
= 2x,
y
=
![]()
,
x
= 0,
y
= 0,
вокруг
оси
Ox.
5.42.
y
= x(3
– x),
y
= x,
вокруг оси: а)
Ox,
б)
Oy.
5.43.
y
= cos
x,
y
= 1,
0
≤
x
≤ 2π,
вокруг
оси
Oy.
5.44.
y
= ex+6,
y
= e2x,
x
= 0, вокруг оси: а)
Ox,
б)
Oy.
5.45.
y
=![]()
,
y
= 0, x
≥ 1, вокруг оси Ox.
5.46.
y
=![]()
,
y
= 0, x
≥ 0, вокруг оси Ox.
5.47.
y
=![]()
,
y
= 0, вокруг оси Oy,
![]()
.
5.48.
x
= 4t2,
y
=
![]()
(петля), вокруг оси Ox.
5.49.
x
= a
ch3
t,
y
=
a
sh3
t,
x
=
2
a,
вокруг
оси
Ox.
5.50.
r
= 2cos2
,
вокруг полярной оси.
5.51.
r
=
![]()
,
0 ≤
≤
,
вокруг полярной оси.
Решение.
5.40. Вычислим объем
полученный вращением вокруг оси Ox.
Имеем
V
=
![]()
=
![]()
=
![]()
.
Теперь вычислим
объем тела, получаемого при вращении
фигуры вокруг оси Oy:
V
=
![]()
=
![]()
=

=
= ![]()
.
5.41. Абсцисса точки
пересечения графиков (рис. 2.20) равна 1.
Искомый объем выражается суммой двух
интегралов:
V
=![]()
+
![]()
=![]()
+![]()
.
В

Рис. 2.20
ычислим интегралы с логарифмом
отдельно, применяя формулу интегрирования
по частям. Имеем
![]()
=
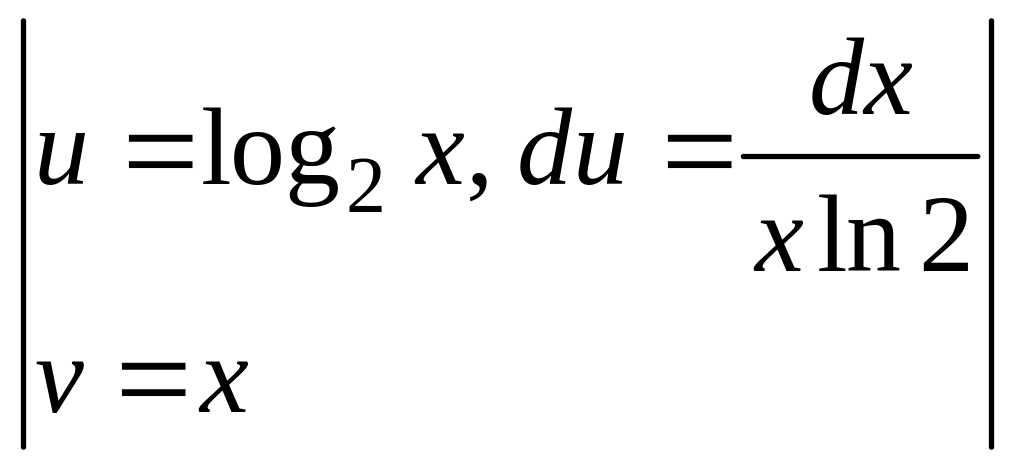
=
=
![]()
.
![]()
=

=
=
![]()
–
![]()
=
=
–
![]()
+
![]()
+ С.
Отсюда получаем,
V
=
![]()
+ 12π –
![]()
+![]()
=

Рис. 2.21
= –
![]()
+
![]()
– 4π.
5.42. Несложно
находится абсцисса точки пересечения
графиков x
= 2 (рис. 2.21). Вычисляем объем, получаемый
при вращении фигуры вокруг
оси Ox:
V
=
![]()
=
=
![]()
=
=![]()
=
![]()
.
При вычислении
объема, получающегося при вращении
вокруг оси Oy,
воспользуемся следующей формулой:
V
=
![]()
–
![]()
,
где y1
= 3x
– x2,
y2
=
x.
Тогда
V
=
![]()
–
![]()
=
![]()
=
![]()
.
5.43. Рассмотрим два
способа вычисления искомого объема.

а б
Рис. 2.22
Решение уравнения
cos
x
= y
при 0≤ x
≤ π относительно x
есть
x
= arccos
y,
решением уравнения cos
x
= y
при π ≤ x
≤ 2π является
x
=2π – arccos
y.
Тогда объем можно вычислить следующим
образом (рис. 2.22, б):
V
=![]()
=
![]()
=
=
![]()
= 4π3.
Но можно, используя
другую формулу, вычислять объем и так
(рис. 2.22, а),
где
![]()
:
V
= 8π3 –
![]()
= 8π3 –
![]()
=
= 8π3 – 4π3
= 4π3,
где слагаемое 8π3
есть объем цилиндра, у которого в
основании – круг радиуса 2π и высота
равна 2.
5

Рис. 2.23
.44. Абсцисса точка пересечения
графиков равна ln
3 (рис. 2.23).
Вычисляем вначале
объем тела, получаемого при вращении
фигуры вокруг оси Ox.
V
=
![]()
=
=
![]()
= (8 + 36 ln 3) .
Для вычисления
объема тела, получаемого вращением
фигуры вокруг оси Oy,
мы, чтобы не искать обратные функции,
воспользуемся следующей формулой:
V
=
![]()
–
![]()
,
где
y1
=
ex
+
6,
y2
=
e2x.
Тогда
V
=
![]()
+
![]()
–
![]()
= 6π ln2
3 +
![]()
–
=
![]()
= 6π ln2
3 +
![]()
=
= 3π
ln 3(ln 9 – 1).
5.45. Объем тела
выражается несобственным интегралом
V
=
![]()
=
![]()
=
![]()
.
5.46. Вычисляем объем
V
=
![]()
=
![]()
=
![]()
=
=
![]()
=
.
5.47. Объем можно
вычислить двумя способами.
Найдя обратную
функцию (x
≥ 0), из
уравнения y
=
,
x
=![]()
,
приходим к интегралу
V
=
![]()
.
Можно использовать
формулу
V
=
![]()
=
![]()
=
![]()
=
![]()
= π.
Мы видим, что в
этом примере второй способ вычисления
предпочтительнее.
5.48. Петля симметрична
относительно оси Ox,
верхняя часть петли есть график функции
y
=
![]()
,
0 ≤ x ≤ 12,
и соответствует
изменению параметра t
от 0 до
.
Вычисляем объем
V
=
![]()
=

=
=
![]()
= 48π.
5.49. В
декартовых координатах уравнение линии
выглядит так:
![]()
=![]()
.
Отсюда заключаем, что линия симметрична
относительно оси Ox,
ясно так же, что a≤
x
≤
![]()
a.
Верхняя ветвь (y
≥ 0)
соответствует изменению параметра t
от 0 до
![]()
(решения уравнений
![]()
).![]()
Вычисляем объем тела, полученного
вращением вокруг оси Ox
верхней ветви кривой (y
≥ 0),
V
=
![]()
=
![]()

![]()
=
![]()
5.50.
Линия представляет собой два симметричных
относительно оси Oy
лепестка, симметричных, в свою очередь,
относительно оси Ox
(рис. 2.24).
Первый соответствует изменению параметра
от –
до
,
второй – от
до π и
от –π до –
.
Вычислим объем тела, получаемого
вращением половины лепестка, и удвоим
результат:
V
=

=

Рис. 2.24
=
=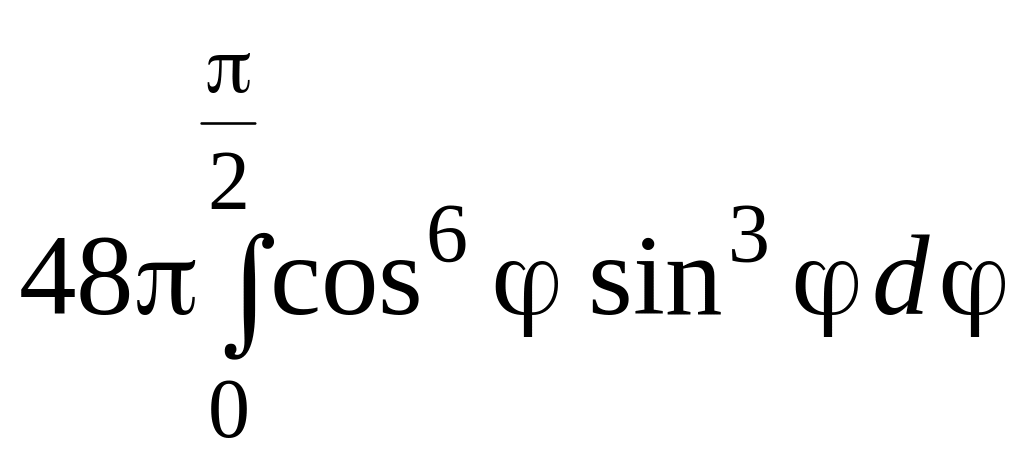
=
=

=

=
=
![]()
=
![]()
=
![]()
=
![]()
.
Минус
перед первым интегралом поставлен
потому, что x
= r
cos
= = 2
cos3
при изменении
от 0 до
![]()
убывает. Действительно,
V
=
![]()
=

=
=

=

.
5.51.
Вычисляем объем
![]()
при
![]()
:
V
=
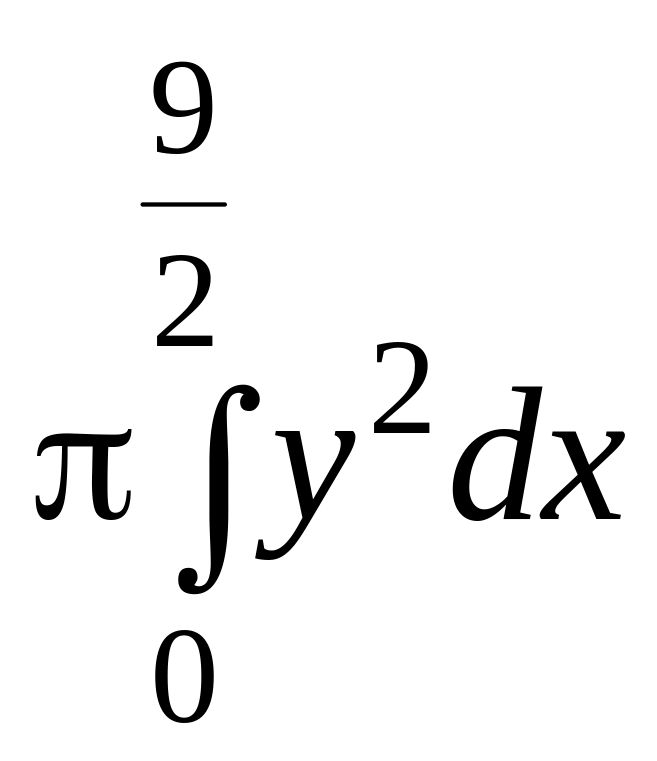
=

=
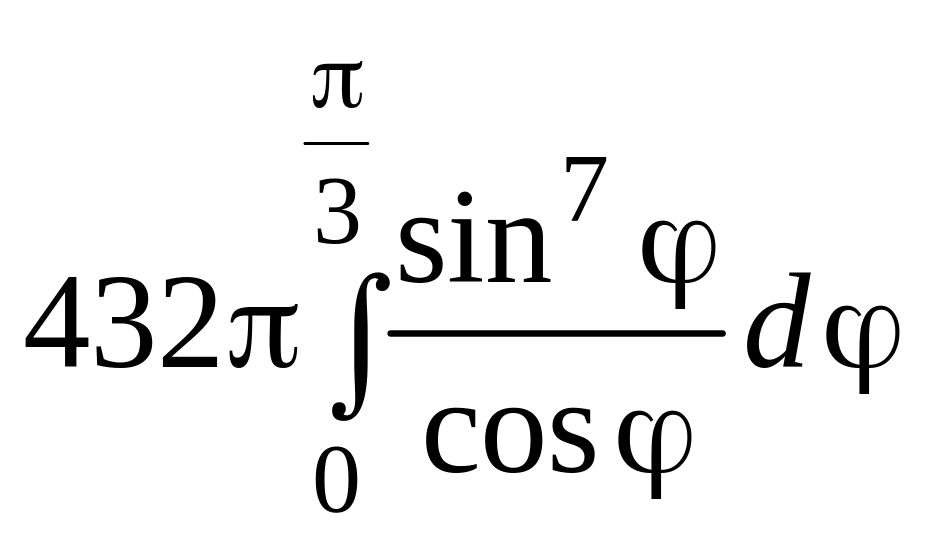
=
=

=

=
= 
=
![]()
.
Найти площадь
поверхности, образованной при вращении
дуги кривой.
5.52.
y2
= 2x,
2x
= 3, вокруг
оси Ox.
5.53.
y
= 3 c
h![]()
,
–1
≤ x
≤ 1, вокруг
оси Ox.
5.54.
y
= cos
2x,
≤ x
≤
![]()
,
вокруг оси Ox.
5.55.
![]()
,
вокруг оси Oy.
5.56.
x
=
![]()
,
y
=
![]()
,
0 ≤
t
≤
π,
вокруг
оси
Ox.
5.57.
x
=
2cos
t
– cos2
t,
y
= 2sin
t
– sin2
t,
0 ≤ t
≤
π,
вокруг
оси
Ox.
5.58.
y
=
(arcsin
x
+
![]()
),
0 ≤
x ≤
1, вокруг
оси
Oy.
5.59.
r
=
![]()
,
вокруг полярной оси.
Решение.
5.52. Достаточно
рассмотреть поверхность, образованную
вращением кривой y
=![]()
,
0 ≤ x
≤ 3/2, вокруг
оси Ox.
Имеем
S
=

=
=

=
=
![]()
=
![]()
.
5.53.
S
=
![]()
=
![]()
=
![]()
=
=
![]()
=
![]()
+6![]()
.
5

Рис. 2.25
.54.
S
=
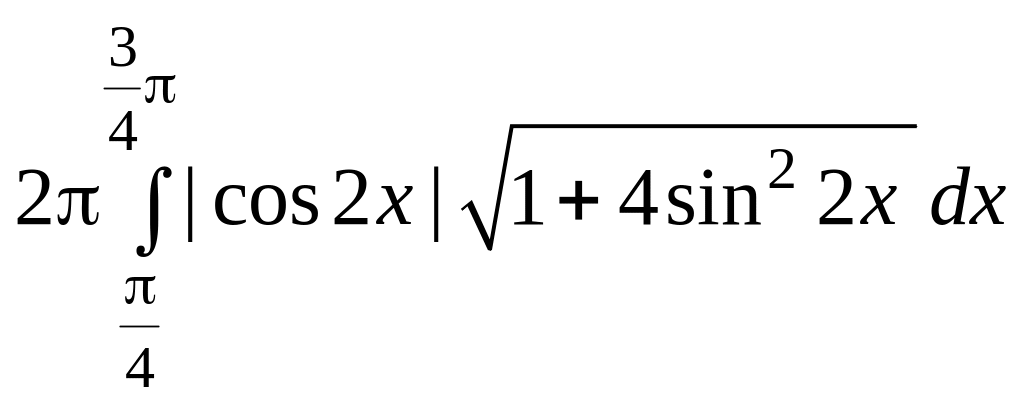
=

=
=

=
![]()
=
=![]()
=
![]()
.
5.55. Используем
формулу
S
=![]()
.
Имеем


Используя результаты
задачи 3.6 из гл. 1, § 3, получаем
![]()
5.56.
y
=![]()
при изменении t
от 0 до
,
при этом x
возрастает от 0 до
.
Когда t
возрастает от
до π,
переменная x
убывает от
до 0, при этом
y
=![]()
.
Таким образом,
наша линия – петля, симметричная
относительно оси Ox.
Поэтому
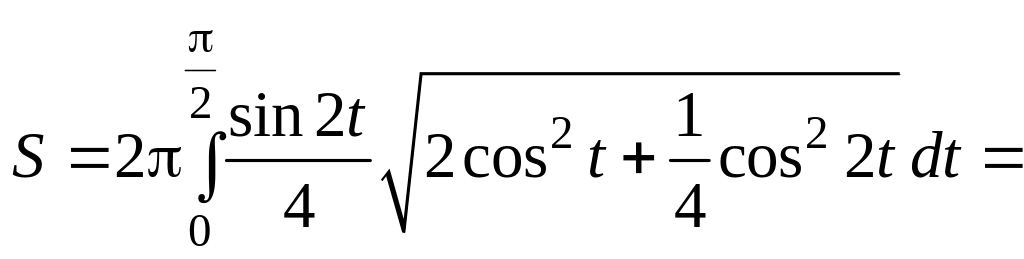
=

=

=
=
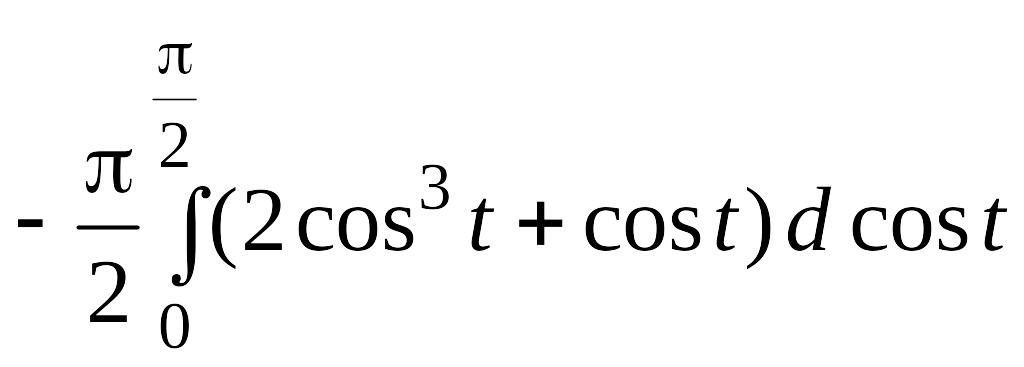
=

=
.
5.57. Вычислим
предварительно дифференциал длины дуги
dl
= = ![]()
.
dl
=
![]()
=
![]()
=
=
4|sin![]()
|dt
= 4 sin
dt,
так как
![]()
.
Вычисляем площадь поверхности вращения
![]()
![]()
5.58. Выражать в
данном случае x
через y
было бы крайне затруднительно. Поэтому
параметризуем кривую, взяв за параметр
x
= t.
Тогда
S
=
![]()
=
![]()
=
=
![]()
=

=
![]()
=
![]()
,
так как
![]()
=
![]()
=
![]()
.
5.59. Линия представляет
собой два лепестка, симметричные
относительно обеих осей координат Ox
и Oy
(x
= r
cos
= 3 cos
![]()
,
y
= r
sin
= 3 sin
).
Достаточно рассмотреть дугу кривой,
соответствующую изменению
от 0 до
![]()
и затем удвоить результат. Вычисляем
площадь поверхности вращения
![]()
S
=

=
=

=
![]()
=
![]()
.
Как найти ось симметрии
2 методика:Нахождение оси симметрии для квадратного трехчленаНахождение оси симметрии графическим способом
Многие характеристики графика функции или многочлена невозможно объяснить без визуального представления. Одна из таких характеристик – ось симметрии: вертикальная линия на графике, которая делит этот график на два зеркально симметричных изображения. Найти ось симметрии для данного многочлена относительно несложно. Существует два основных способа.
Шаги
Метод 1 из 2: Нахождение оси симметрии для квадратного трехчлена
-

1
Определите, какова степень многочлена. Степень многочлена – это наибольшая степень, которую имеют одночлены в этом выражении. Если степень данного многочлена равна 2 (ни один одночлен в выражении не имеет степени выше, чем x2), вы можете найти ось симметрии, используя данный способ. Если степень многочлена больше двух, применяйте второй способ.- Чтобы наглядно продемонстрировать этот способ, возьмем, например, многочлен вида 2×2 + 3x – 1. Самая высокая степень в многочлене – x2, следовательно, мы имеем дело с квадратным трехчленом и можем воспользоваться первым способом для нахождения оси симметрии.
-

2
Подставьте коэффициенты в формулу расчета оси симметрии. Для нахождения оси симметрии для квадратного трехчлена вида ax2 + bx +c (парабола), применяют базовую формулу x = -b / 2a.- В нашем примере a = 2, b = 3, and c = -1. Подставим эти значения в нашу формулу, и получаем:
x = -3 / 2(2) = -3/4.
- В нашем примере a = 2, b = 3, and c = -1. Подставим эти значения в нашу формулу, и получаем:
-

3
Запишите уравнение оси симметрии. Значение, которое вы рассчитали по формуле оси симметрии, это значение точки пересечения оси симметрии с осью абсцисс.- В вышеприведенном примере, ось симметрии равна -3/4.
Метод 2 из 2: Нахождение оси симметрии графическим способом
-

1
Определите степень многочлена. Степень многочлена – это наибольшая степень, которую имеют одночлены в этом выражении. Если степень данного многочлена равна 2 (ни один одночлен в выражении не имеет степени выше, чем x2), вы можете найти ось симметрии, используя вышеприведенный способ. Если степень многочлена больше 2, применяйте графический способ. -

2
Начертите систему координат. Нарисуйте две линии, пересекающиеся под прямым углом в виде знака “плюс”. Горизонтальная линия будет осью х, а вертикальная – осью у. -

3
Отложите единичные числовые отрезки на осях. Отложите на осях числовые отрезки равной величины. -

4
Рассчитайте значение y = f(x) для каждого значения х. Возьмите данный многочлен или функцию и рассчитайте значения f(x), последовательно подставив в выражение значения х. -

5
Отметьте точки на графике для каждой пары координат. Теперь у вас есть соответствующее значение y = f(x) для каждого значения на оси абсцисс. Для каждой точки с координатами (x, y), отметьте точку в системе координат – по вертикали отложив значение по оси Х, а по горизонтали – на оси Y. -

6
Нарисуйте график многочлена. Когда вы нанесли все точки на систему координат, можно плавно соединить их между собой. У вас получится непрерывный график вашего многочлена. -

7
Найдите ось симметрии. Внимательно изучите полученный график. Найдите точку на графике, по которой можно провести линию, разделяющую график на две равные, зеркальные половины. -

8
Отметьте ось симметрии. Если вы нашли такую точку (назовем ее “b”) на оси х, которая разделяет график на две зеркальные половины, это значение и будет искомою осью симметрии.
Советы
- Длина ваших осей абсцисс и ординат должна быть достаточной, чтобы наглядно отобразить форму графика.
- Некоторые многочлены не имеют оси симметрии. Например, для y = 3x не существует оси симметрии.
- Симметрия многочлена может быть определена как четная или нечетная. Любой график, ось симметрии которого совпадает с осью у имеет “четную” симметрию. Любой график, ось симметрии которого совпадает с осью х – “нечетный.”
Длина дуги параболы
Длина дуги параболы — это число, характеризующее протяжённость дуги параболы в единицах измерения длины.
Содержание
[править] Обозначения
x1 — абсцисса первой точки дуги;
y1 — ордината (меньшая) первой точки дуги;
x2 — абсцисса второй точки дуги;
y2 — ордината (большая) второй точки дуги;
y 2 = 2px — каноническое уравнение параболы;
Lдуг.пар — длина дуги параболы.
[править] Формула
- Заметим, что формула верна для точек с положительными и отрицательными ординатами, причём y2 > y1.
[править] Вывод формулы
- Для вывода используется формула длина дуги плоской кривой в прямоугольных координатах.
- Для нахождения интеграла используется формула 1 интегралы функций с корнями.
[править] Другие формулы
- ; ;
- длина дуги параболы; ; ; ; ; ; ; ; ; ; ; ; ; .
Персональные инструменты
Пространства имён
- Статья
- Обсуждение
Варианты
Просмотры
- Читать
- Правка
- История
Действия
Поиск
Навигация
Инструменты
- Последнее изменение этой страницы: 12:42, 6 октября 2021.
- К этой странице обращались 23 168 раз.
Текст страницы доступен по условиям лицензии GNU Free Documentation License. Материалы могут быть скопированы при условии указания активной ссылки на источник копирования в теле статьи (на той же странице). В отдельных случаях могут действовать условия лицензии Creative Commons Attribution-ShareAlike (CC BY-SA 3.0), информацию об этом можно просмотреть на странице обсуждения или в истории правок. В частности, условия лицензии CC BY-SA 3.0 действуют в отношении статей, перенесенных из Википедии (указание на факт переноса всегда есть в истории правок статьи или на ее странице обсуждения).
В текстах упоминаются организации, признанные на территории Российской Федерации террористическими и/или в отношении которых судом принято вступившее в законную силу решение о запрете деятельности. В том числе:
Признаны террористическими организациями: «Исламское государство» (другие названия: «Исламское Государство Ирака и Сирии», «Исламское Государство Ирака и Леванта», «Исламское Государство Ирака и Шама»), «Высший военный Маджлисуль Шура Объединенных сил моджахедов Кавказа», «Конгресс народов Ичкерии и Дагестана», «База» («Аль-Каида»), «Братья-мусульмане» («Аль-Ихван аль-Муслимун»), «Движение Талибан», «Имарат Кавказ» («Кавказский Эмират»), Джебхат ан-Нусра (Фронт победы) (другие названия: «Джабха аль-Нусра ли-Ахль аш-Шам» (Фронт поддержки Великой Сирии), Всероссийское общественное движение «Народное ополчение имени К. Минина и Д. Пожарского», Международное религиозное объединение «АУМ Синрике» (AumShinrikyo, AUM, Aleph) — см. полный список.
Деятельность запрещена по решению суда: Межрегиональная общественная организация «Национал-большевистская партия», Межрегиональная общественная организация «Движение против нелегальной иммиграции», Украинская организация «Правый сектор», Украинская организация «Украинская национальная ассамблея — Украинская народная самооборона» (УНА — УНСО), Украинская организация «Украинская повстанческая армия» (УПА), Украинская организация «Тризуб им. Степана Бандеры», Украинская организация «Братство», Межрегиональное общественное объединение — организация «Народная Социальная Инициатива» (другие названия: «Народная Социалистическая Инициатива», «Национальная Социальная Инициатива», «Национальная Социалистическая Инициатива»), Межрегиональное общественное объединение «Этнополитическое объединение „Русские“», Общероссийская политическая партия «ВОЛЯ», Общественное объединение «Меджлис крымскотатарского народа», Религиозная организация «Управленческий центр Свидетелей Иеговы в России» и входящие в ее структуру местные религиозные организации, Межрегиональное общественное движение «Артподготовка» — см. полный список.
Вычисление длин дуг плоских кривых
В элементарной геометрии измерялись длины прямолинейных отрезков, а также длина окружности и ее частей. За длину окружности принимается предел периметров правильных вписанных в окружность многоугольников при неограниченном увеличении числа их сторон. Обобщим это понятие для любой кривой.
Определение.ДлинойL дуги АВ называется предел, к которому стремится периметр вписанной в эту дугу ломанной, когда число ее звеньев неограниченно растет, а наибольшая из длин звеньев стремится к нулю:
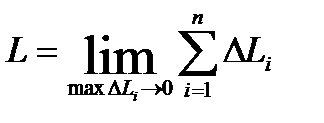
Кривые, для которых этот предел существует, называются спрямляемыми.
Теорема.Пусть криваяАВ задана уравнением y=f(x), где f(x) – непрерывная функция, имеющая непрерывную производную во всех точках сегмента [a;b]. Тогда дуга АВ имеет длину:
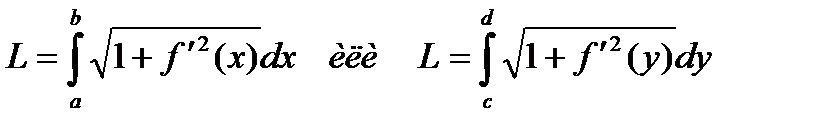 ,
,
Пример 2.Вычислить длину дуги параболы у 2 =4х от х=0 до х=1.
Для наглядности выполним чертеж.
Для этого выразим из уравнения параболы х и найдем производную по «игреку»:
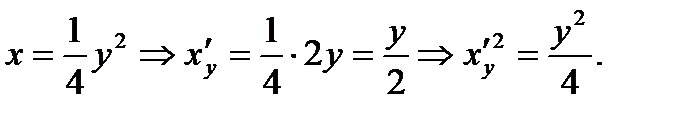
Тогда длина дуги будет равна:
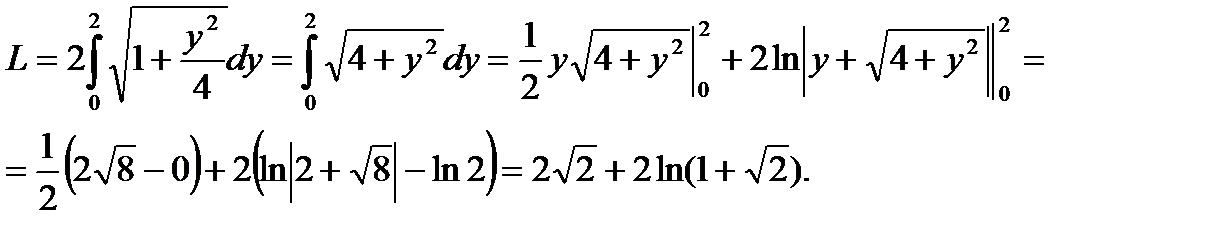
Замечание. 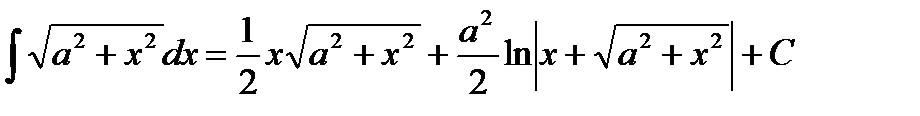
Парабола свойства и график квадратичной функции
Что такое парабола знают, пожалуй, все. А вот как ее правильно, грамотно использовать при решении различных практических задач, разберемся ниже.
Сначала обозначим основные понятия, которые дает этому термину алгебра и геометрия. Рассмотрим все возможные виды этого графика.
Узнаем все основные характеристики этой функции. Поймем основы построения кривой (геометрия). Научимся находить вершину, другие основные величины графика данного типа.
Узнаем: как правильно строится искомая кривая по уравнению, на что надо обратить внимание. Посмотрим основное практическое применение этой уникальной величины в жизни человека.
Что такое парабола и как она выглядит
Алгебра: под этим термином понимается график квадратичной функции.
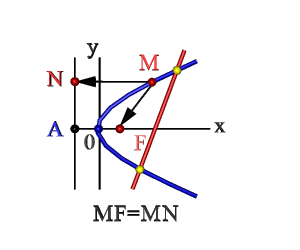
Геометрия: это кривая второго порядка, имеющая ряд определенных особенностей:
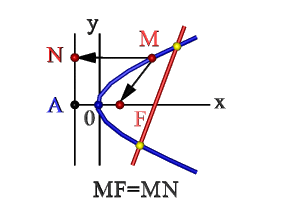
- Любая прямая пересекает на плоскости искомую линию в 2-х точках – так называемые, «нули» (кроме основного экстремума графика).
- Множество точек плоскости ХОY (М), расстояние FM которых до F = расстоянию MN до прямой Где F – фокус, AN – директриса. Эти понятия рассмотрим ниже.
Каноническое уравнение параболы
На рисунке изображена прямоугольная система координат (XOY), экстремум, направление ветвей чертежа функции вдоль оси абсцисс.
Каноническое уравнение имеет вид:
где коэффициент p – фокальный параметр параболы (AF).
В алгебре оно запишется иначе:
y = a x2 + b x + c (узнаваемый шаблон: y = x2).
Свойства и график квадратичной функции
Функция обладает осью симметрии и центром (экстремум). Область определения – все значения оси абсцисс.
Область значений функции – (-∞, М) или (М, +∞) зависит от направления ветвей кривой. Параметр М тут означает величину функции в вершине линии.
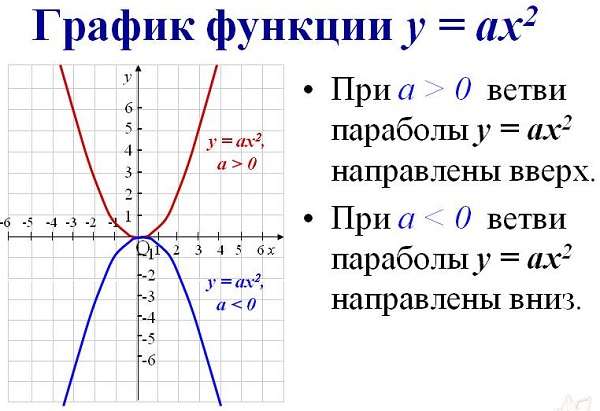
Как определить, куда направлены ветви параболы
Чтобы найти направление кривой такого типа из выражения, нужно определить знак перед первым параметром алгебраического выражения. Если а ˃ 0, то они направлены вверх. Если наоборот – вниз.
Как найти вершину параболы по формуле
Нахождение экстремума является основным этапом при решении множества практических задач. Конечно, можно открыть специальные онлайн калькуляторы, но лучше это уметь делать самому.

Как же ее определить? Есть специальная формула. Когда b не равно 0, надо искать координаты этой точки.
Формулы нахождения вершины:
- x0 = -b / (2 * a),
- y0 = y (x0).
Пример.
Имеется функция у = 4 * x2 + 16 * x – 25. Найдём вершины этой функции.
Для такой линии:
- х = -16 / (2 * 4) = -2,
- y = 4 * 4 — 16 * 2 — 25 = 16 — 32 — 25 = -41.
Получаем координаты вершины (-2, -41).
Смещение параболы
Классический случай, когда в квадратичной функции y = a x2 + b x + c, второй и третий параметры равны 0, а = 1 – вершина находится в точке (0, 0).
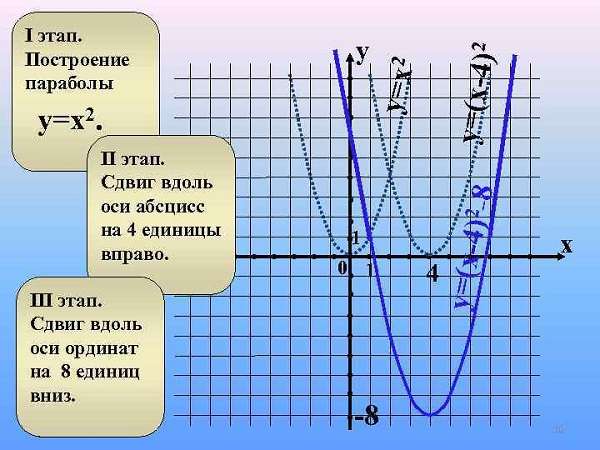
Движение по осям абсцисс или ординат обусловлено изменением параметров b и c соответственно. Сдвиг линии на плоскости будет осуществляться ровно на то количество единиц, чему равно значение параметра.
Пример.
Имеем: b = 2, c = 3.
Это означает, что классический вид кривой сдвинется на 2 единичных отрезка по оси абсцисс и на 3 по оси ординат.
Как строить параболу по квадратному уравнению
Школьникам важно усвоить, как правильно начертить параболу по заданным параметрам.
Анализируя выражения и уравнения, можно увидеть следующее:
- Точка пересечения искомой линии с вектором ординат будет иметь значение, равное величине с.
- Все точки графика (по оси абсцисс) будут симметричны относительно основного экстремума функции.
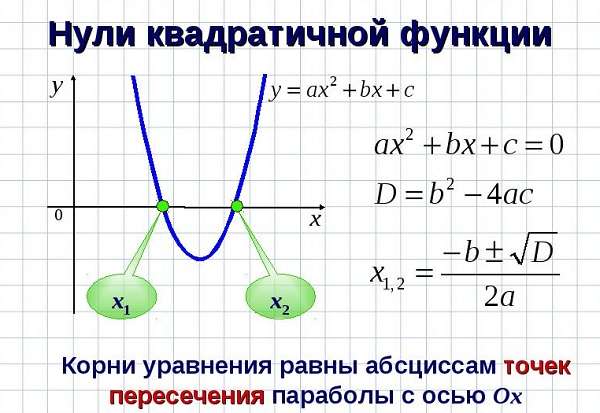
Кроме того, места пересечения с ОХ можно найти, зная дискриминант (D) такой функции:
Для этого нужно приравнять выражение к нулю.
Наличие корней параболы зависит от результата:
- D ˃ 0, то х1, 2 = (-b ± D0,5) / (2 * a),
- D = 0, то х1, 2 = -b / (2 * a),
- D ˂ 0, то нет точек пересечения с вектором ОХ.
Получаем алгоритм построения параболы:
- определить направление ветвей,
- найти координаты вершины,
- найти пересечение с осью ординат,
- найти пересечение с осью абсцисс.
Пример 1.
Дана функция у = х2 5 * х + 4. Необходимо построить параболу. Действуем по алгоритму:
- а = 1, следовательно, ветви направлены вверх,
- координаты экстремума: х = (-5) / 2 = 5/2, y = (5/2)2 — 5 * (5/2) + 4 = -15/4,
- с осью ординат пересекается в значении у = 4,
- найдем дискриминант: D = 25 — 16 = 9,
- ищем корни:
- Х1 = (5 + 3) / 2 = 4, (4, 0),
- Х2 = (5 — 3) / 2 = 1, (1, 0).
По полученным точкам можно построить параболу.
Пример 2.
Для функции у = 3 * х2 2 * х 1 нужно построить параболу. Действуем по приведенному алгоритму:
- а = 3, следовательно, ветви направлены вверх,
- координаты экстремума: х = (-2) / 2 * 3 = 1/3, y = 3 * (1/3)2 — 2 * (1/3) — 1 = -4/3,
- с осью у будет пересекаться в значении у = -1,
- найдем дискриминант: D = 4 + 12 = 16. Значит корни:
- Х1 = (2 + 4) / 6 = 1, (1,0),
- Х2 = (2 — 4) / 6 = -1/3, (-1/3, 0).
По полученным точкам можно построить параболу.
Директриса, эксцентриситет, фокус параболы
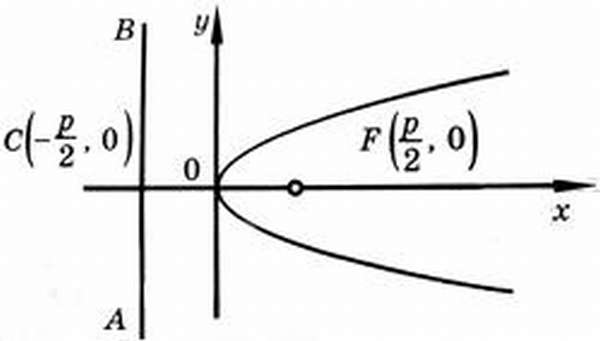
Исходя из канонического уравнения, фокус F имеет координаты (p/2, 0).
Прямая АВ – директриса (своего рода хорда параболы определенной длины). Ее уравнение: х = -р/2.

Эксцентриситет (константа) = 1.
Заключение
Мы рассмотрели тему, которую изучают школьники в средней школе. Теперь вы знаете, глядя на квадратичную функцию параболы, как найти её вершину, в какую сторону будут направлены ветви, есть ли смещение по осям, и, имея алгоритм построения, сможете начертить её график.

