Содержание
- 23. Масштаб
- 70. Определить длину отрезка на местности, если на плане она равна 2,5см, а масштаб 1:1000.
- 71. Особенности проектирования безнапорной канализации и автодороги.
- 72. Определение расстояния до недоступного предмета.
- Масштабы
- Масштабы.
- Понятие карты, плана, профиля.
- Стандартные масштабы
- Решение задач по топогра- фическим планам
- Масштабы: численный, линейный и поперечный
- Масштабом
- горизонтальным проложением линии
- численный, линейный и поперечный.
- Численным масштабом
- Линейный масштаб
- Поперечный масштаб
- Чтение топографических планов
- Задачи, решаемые по топографическим планам
- Определение прямоугольных координат точек
- Измерение длин линий
- Определение дирекционного угла
- Определение отметок точек и крутизны ската линии местности
23. Масштаб

Участки земной поверхности изображают на бумаге в уменьшенном виде. Например, отрезок 1000 м изображают на карте (рис. 35) отрезком в 1 см. Так как 1000 м = 100000 см, то каждый отрезок на карте в 100000 раз меньше соответствующего отрезка на местности.
- Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.
В рассмотренном нами примере масштаб карты равен  Говорят, что карта сделана в масштабе одна стотысячная.
Говорят, что карта сделана в масштабе одна стотысячная.
Задача 1. Длина отрезка на карте 3 см. Найдём длину соответствующего отрезка на местности, если масштаб карты 1 : 1 000000.
Р е ш е н и е. Обозначим длину отрезка на местности (в сантиметрах) буквой х и найдём отношение длины отрезка на карте к длине отрезка на местности: 3:*, которое и будет равно масштабу карты.
Значит, 3 : х = 1 : 1 000000.
Решив уравнение, получим х = 3 • 1 000000 = 3000000. Но 3000000 см = = 30000 м = 30 км.
Ответ: длина отрезка на местности 30 км.
Задача 2. Длина отрезка на местности 4,5 км. Чему равна длина этого отрезка на карте, сделанной в масштабе 1 : 100000?
Р е ш е н и е. Обозначим длину (в километрах) отрезка на карте буквой х и составим пропорцию: х : 4,5 = 1 : 100000.
Решив уравнение, получим х = 4,5 : 100000 = 0,000045.
Но 0,000045 км = 0,045 м = 4,5 см.
Ответ: длина отрезка на карте 4,5 см.
Что называют масштабом карты?
Чему равен масштаб чертежа, если на нём детали увеличены в 5 раз? уменьшены в 50 раз?

820. Определите по карте (рис. 36) расстояние от опушки леса (точка А) до точки пересечения дороги с рекой. Масштаб карты 1 : 100 000.
821. Расстояние между городами А и Б на карте равно 8,5 см. Найдите расстояние между городами на местности, если масштаб карты 
Источник
70. Определить длину отрезка на местности, если на плане она равна 2,5см, а масштаб 1:1000.
2,5*1000 = 2500см = 25м
71. Особенности проектирования безнапорной канализации и автодороги.
Проектирование линейных сооружений сводится к построению проектной линии будущего сооружения на продольном профиле земли.
Трассы делятся на участки в пределах которых сохраняется постоянный уклон.
На опорные трубопроводы проектируют в соответствии с профилем земли, т.е. горизонтальные и вертикальные кривые отсутствуют.
Для подземных трубопроводов есть ряд ограничений. Для каждого вида индивидуальны, например:
Безнапорные трубопроводы (канализация) проектируют с постоянным понижением.
Смотровые колодцы проектируют через определенные расстояния. От одного колодца до другого уклон постоянный. Если трасса поворачивает, то в определенном месте ставится переносный колодец (вода поступает на одной отметке, а вытекает на более низкой)
Уклоны проектируют в диапазоне от min до max. Горизонтальные участки отсутствуют.
Автомобильные дороги тоже проектируются по участкам, здесь возможны горизонтальные участки, дороги могут проектироваться как выше, так и ниже профиля земли (досыпают или срезают) .
72. Определение расстояния до недоступного предмета.
Метод обхода реализуют проложение теодолитного хода по контуру снимаемого объекта с привязкой этого хода к съемочному обоснованию. Углы 1,…, n снимают при одном положении круга теодолита, а измерения длин сторон осуществляют землемерной лентой или рулеткой, нитяным дальномером или светодальномером электронного тахеометра.
Метод обхода используют, как правило, в закрытой местности для обозначения недоступных объектов значительной площади.
Источник
Масштабы



Масштабы.
Понятие карты, плана, профиля.
При изображении физической поверхности Земли на картах её проектируют на поверхность эллипса, а затем его разворачивают в плоскость. Таким образом, картой называют уменьшенное и закономерно искаженное изображение Земли или отдельных частей её поверхности на плоскости.
Иначе поступают с изображением плана. Физическую поверхность Земли ортогонально проектируют на горизонтальную плоскость. Таким образом, планомназывают уменьшенное и подобное изображение ортогональной проекции местности, в пределах которой кривизна уровенной поверхности не учитывается Ортогональная проекция—изображение пространственного объекта на плоскости посредством проектирующих лучей, перпендикулярных к плоскости проектирования. Длина ортогональной проекции линии на горизонтальную плоскость называется горизонтальным проложением. По назначению топографические карты и планы делятся на основные и специализированные. К основным относятся карты и планы общегосударственного картографирования. Эти материалы многоцелевого назначения, поэтому на них отображают все элементы ситуации и рельефа. Специализированные карты и планы создают для решения конкретных задач отдельной отрасли. Так, дорожные карты содержат более детальную характеристику дорожной сети. К специализированным относят и изыскательские планы, используемые только в период проектирования и строительства зданий и сооружений. На этих картах только часть нумерованных объектов изображаются точно, все остальные — схематически. Кроме планов и карт к топографическим материалам относят профили местности, представляющие собой уменьшенное изображение вертикального разреза земной поверхности вдоль выбранного направления. Профили местности являются топографической основой при составлении проектно-технической документации, необходимой при строительстве подземных и наземных трубопроводов, дорог и других коммуникаций.
На топографических картах все объекты земного изображаются максимальной точностью, независимо от значимости объекта.
Стандартные масштабы
Масштабы топокарт: Масштабы планов:
Отношение длины линии на плане к длине горизонтального проложения этой линии на местности называется численным масштабом топографического плана. Его обычно представляют в виде правильной дроби, числитель которой равен единице, а знаменатель — некоторому числу N, показывающему, во сколько раз расстояние на плане ab уменьшено по сравнению с соответствующим горизонтальным проложением Ао Во линии местности.
Так, при аЬ=5см и АоВо=250м имеем
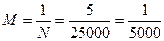 (1.1)
(1.1)
При сравнении численных масштабов различных планов употребляют термины: «мельче» и «крупнее». Если N1 * 100+4(0,1 * 100)+3,5(0,01 * 100)=143,5м
Невооруженный глаз человека способен на чертеже, на расстоянии 20-25см увидеть точку равную 0,1мм. Поэтому точностью масштаба называют длину горизонтальной проекции на местности, соответствующую 0,1мм на карте или плане. Для масштаба 1:500; 1:1000; 1:10000; 1:25000; точность масштаба соответственно равно 0,05м; 0,1м; 1,0м; 2,5м.
Пример1. Дано расстояние между двумя точками на карте равное 56,4мм. Определить длину горизонтального проложения соответствующей линии местности, если масштаб карты равен 1:2000.
Решение. Вычисление производится по формуле
где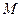 — знаменатель численного масштаба, показывающий во сколько раз линии местности уменьшены при их изображении на карте;
— знаменатель численного масштаба, показывающий во сколько раз линии местности уменьшены при их изображении на карте;
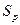 — длина линии на плане или карте;
— длина линии на плане или карте;
Sm — горизонтального проложения соответствующий линии на местности.
Пример2. Дано горизонтальное проложение линий местности равное 78,0м. Определить с точностью 0,1 мм длину соответствующей линии на карте в масштабе 1:2 000
Решение. Вычисление выполняют по формуле:
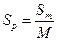
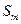 =78,0м=78000мм, то
=78,0м=78000мм, то 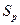 =78000:2000=39,0мм на карте масштаба 1:2000.
=78000:2000=39,0мм на карте масштаба 1:2000.
Пример3. Определить длину отрезка на плане масштаба 1:1000, если длина линии на местности равна 35.6м.
Так же как и в предыдущей задаче необходимо мысленно оцифровать деления поперечного масштаба. Так, если масштаб плана 1:1000, то основание поперечного масштаба равно 20 м., АВ=2м и наименьшее деление (а1 в1) равно 0.2м. А затем суммированием этих отрезков набрать длину линии на поперечном масштабе. Т.е.35.6:20м =1 (целое основание масштаба). Осталась длина линии 15.6. Ее делим на цену деления основания масштаба 15.6:2м=7 (целых делений основания масштаба. 7х2м=14м. 15.6-14м=1.6м. 1.6м:0.2м=8 (наименьших делений масштаба). После этого устанавливаем измеритель на поперечном масштабе так, чтобы между иголками измерителя уложилось 1 целое основание масштаба, 7 целых целений основания масштаба и 8 наименьших делений масштаба.
Пример4.На карте масштаба 1:2000 был измерен отрезок, длинной 2.5 см. Найти длину линии на местности, соответствующую этому отрезку.
Так как задан численный масштаб 1:2000 значит в этом масштабе 1см. на карте соответствует 2000 см. или 20 м на местности, тогда в 2.5см будет 2.5х20=50м . Ответ: 50м.
Пример5. Найти длину отрезка на плане масштаба 1:500, если длина горизонтального проложения линии на местности 28.50м.
В масштабе 1:500 1см на плане соответствует 5м на местности. По условию задачи на местности 28.5м. Следовательно
1 основание -10м
1 наименьшее деление — 0,1м
Пример6.Определить точность масштаба 1:10 000.
Решение. Так как точность масштаба это длина горизонтальной проекции линии на местности, соответствующая 0.1мм на карте или плане, необходимо вычислить длину линии на местности, соответствующую 0.1мм на карте или плане. По аналогии с предыдущими задачами рассуждаем так 1см на карте масштаба 1:10 000 соответствует 100м на местности, соответственно
Пример7: Перевести численный масштаб 1:10000 в пояснительный.
Решение : Для перевода численного масштаба в пояснительный необходимо от сантиметров в знаменателе перейти к метрам;
1/10000:100 или 1 см-100 м .
Вопросы для самопроверки:
1. Что изучает геодезия?
2. Виды геодезии?
3. Какие задачи решает инженерная геодезии?
4. Что представляет собой действительная фигура Земли?
5. Почему изображение фигуры Земли заменяют референц-эллипсоидом или шаром?
6. Что такое уровенная поверхность?
7. Что называется планом?
8. Что называется картой?
9. В чем отличия между картой и планом?
10. Что называется профилем местности?
11. Что называется масштабом?
12. Что представляют собой численный и пояснительный масштабы?
13. Перечислите масштабы топографических карт и планов.
14. Что такое точность масштаба?
15. Как построить нормальный сотенный поперечный масштаб?
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: 


Познавательно:
Финансовая система и ее структура Совокупность финансовых отношений в рамках национальной экономики образует финансовую систему государства.
Обстоятельства, исключающие преступность деяния Обстоятельства, исключающие преступность деяния — деяния, формально содержащие в себе признаки объективной стороны.
Метод узловых потенциалов Ток в любой ветви схемы можно найти по обобщенному закону Ома.
Устройство светового микроскопа Микроскоп (от греч. mikros — малый и skopeo — смотрю) — оптический прибор для получения увеличенного изображения мелких объектов и их.
Воспитание, обучение, образование, Среди понятий науки выделяют основные (базовые) категории. Категории пронизывают все научное знание и связывают его в целостную.
Источник
Решение задач по топогра- фическим планам
Масштабы: численный, линейный и поперечный
Масштабом
горизонтальным проложением линии
С помощью масштаба решаются две задачи: 1 — определение длины линии на топографическом плане (карте); 2 — построение заданной линии на топографическом плане (карте).
Применяется три типа масштаба:
численный, линейный и поперечный.
Численным масштабом
Численный масштаб – величина неименованная. Он записывается так: 1:1000, 1:2000, 1: 5000 и т.д., причём в такой записи 1000, 2000 и 5000 называется знаменателем масштаба М.
Численный масштаб говорит о том, что в одной единице длины линии на плане (карте ) содержится точно столько же единиц длины на местности. Так, например, в одной единице длины линии на плане 1:5000 содержится точно 5000 таких же единиц длины на местности, а именно: один сантиметр длины линии на плане 1:5000 соответствует 5000 сантиметрам на местности (т.е. 50 метрам на местности); в одном миллиметре длины линии на плане 1:5000 содержится 5000 миллиметров на местности (т.е. в одном миллиметре длины линии на плане 1:5000 содержится 500 сантиметров или 5 метров на местности) и т.д.
При работе с планом в ряде случаев пользуются линейным масштабом.
Линейный масштаб

Рис.1
Основанием линейного масштаба называется отрезок АВ линейного масштаба (основная доля масштаба), равный обычно 2 см. Он переводится в соответствующую длину на местности и подписывается. Крайнее левое основание масштаба делят на 10 равных частей.
Наименьшее деление основания линейного масштаба равно 1/10 основания масштаба.
Пример: для линейного масштаба (использующегося при работе на топоплане масштаба 1:2000), показанного на рисунке 1, основание масштаба АВ равно 2 см (т.е. 40 метрам на местности), а наименьшее деление основания равно 2 мм, что в масштабе 1:2000 соответствует 4 м на местности.
Отрезок cd (рис. 1), взятый с топографического плана масштаба 1:2000, состоит из двух оснований масштаба и двух наименьших делений основания, что, в итоге, соответствует на местности 2х40м+2х2м = 88 м.
Более точное графическое определение и построение длин линий можно сделать с помощью другого графика — поперечного масштаба (рис. 2).
Поперечный масштаб
Основание AB нормального поперечного масштаба равно, как и в линейном масштабе, также 2 см. Наименьшее деление основания равно CD =1/10 АВ= 2мм. Наименьшее деление поперечного масштаба равно cd = 1/10 CD =1/100 АВ = 0,2мм (что следует из подобия треугольника BCD и треугольника Bcd).
Таким образом, для численного масштаба 1:2000 основание поперечного масштаба будет соответствовать 40 м, наименьшее деление основания (1/10 основания) равно 4 м, а наименьшее деление масштаба 1/100 АВ равно 0,4 м.
Пример: отрезок ав (рис. 2), взятый с плана масштаба 1:2000, соответствует на местности 137,6 м (3 основания поперечного масштаба (3х40=120 м), 4 наименьших деления основания (4х4=16 м) и 4 наименьших деления масштаба (0.4х4=1.6 м), т.е. 120+16+1.6=137.6 м) .
Остановимся на одной из важнейших характеристик понятия «масштаб».
Точностью масштаба называется горизонтальный отрезок на местности, который соответствует величине 0,1 мм на плане данного масштаба. Эта характеристика зависит от разрешающей способности невооруженного человеческого глаза, которая (разрешающая способность) позволяет рассмотреть минимальное расстояние на топографическом плане в 0.1мм. На местности эта величина будет уже равна 0.1 мм х М, где М – знаменатель масштаба.

Рис.2
Поперечный масштаб, в частности, позволяет измерить длину линии на плане (карте) масштаба 1:2000 именно с точностью данного масштаба.
Пример: в 1 мм плана 1:2000 содержится 2000 мм местности, а в 0,1мм, соответственно, 0,1 x М (мм) = 0.1 х 2000 мм = 200 мм = 20 см, т.е. 0,2 м.
Поэтому при измерении (построении) на плане длины линии ее значение следует округлить с точностью масштаба. Пример: при измерении (построении) линии длиной 58,37 м (рис. 3), ее значение в масштабе 1:2000 (с точностью масштаба 0,2 м) округляется до 58,4 м, а в масштабе 1:500 (точность масштаба 0,05 м) – длина линии округляется уже до 58,35 м.

Рис.3
Чтение
топографических планов
Для пользования топографическими планами необходимо изучить условные знаки, принятые для данного масштаба. Условные знаки – графические обозначения, которые показывают местоположение предметов и явлений, а также их количественные и качественные характеристики. Они издаются в виде отдельных таблиц или таблиц на учебных планах. Условные знаки делятся на масштабные (контурные), и внемасштабные.
Масштабными называются условные знаки, которыми местные предметы изображаются в масштабе данного плана, т.е. крупные объекты, например, пашни, луга, леса, моря, озера и т.п.
Внемасштабные условные знаки – знаки, показывающие предметы, которые вследствие своей малости не могут быть изображены в масштабе плана (ширина дорог, колодцы, родники, мосты, опоры ЛЭП, столбы электросети и т.д.). Величина этих знаков не соответствует истинным размерам изображаемых предметов.
Линейные знаки — картографические условные знаки, применяемые для изображения объектов линейного характера, длина которых выражается в масштабе карты, но ширина значительно превышает их фактическую ширину.
Площадные условные знаки — картографические условные, применяемые для заполнения площадей объектов, выражающихся в масштабе карты.
Внемасштабные линейные знаки — картографические условные знаки, применяемые для изображения объектов линейного характера, длина которых не выражается в масштабе карты.
Внемасштабные площадные условные знаки — картографические условные знаки, применяемые для изображения объектов, площади которых не выражаются в масштабе карты (плана).
Пояснительные подписи — подписи, поясняющие вид или род изображенных на карте объектов, а также их количественные и качественные характеристики.
Штриховые элементы карты (плана) — элементы карты (плана), выполненные линиями, штрихами или точками.
Фоновые элементы карты (плана) — элементы карты (плана), выполненные каким-либо цветовым фоном.
Задачи, решаемые
по топографическим планам
По топографическому плану можно решить ряд задач, в том числе определить: прямоугольные координаты точки; длину линии; дирекционный угол и румб линии; отметку точки; уклон, крутизну ската и др. Порядок решения этих задач показан на примере учебного плана масштаба 1:2000.
Определение прямоугольных
координат точек
На топографических планах наносится координатная сетка, образующая квадраты со сторонами 10 см. Вертикальные линии сетки параллельны оси абсцисс, а горизонтальные — оси ординат. Координаты вершин квадратов координатной сетки подписываются. Для быстрого нахождения какой-нибудь точки на топографическом плане указывают нижний левый угол соответствующего квадрата сетки координат.
Пример: запись 79,2 означает, что абсцисса линии сетки Х = 79,2 км, т.е. отстоит по оси Х от начала координат на 79200 м. Запись 66,2 означает, что ордината линии сетки Y = 66,2 км, т.е. отстоит по оси У от начала координат на 66200 м.
Для быстрого нахождения какой-нибудь точки на топогра-фическом плане указывают нижний левый угол соответствующего квадрата сетки координат.
Пример: пользуясь координатной сеткой, циркулем и поперечным масштабом, по топографическому плану можно определить прямоугольные координаты точки А (рис. 4), находящейся в квадрате 79,2 – 66,2. Необходимо помнить, что абсциссы возрастают к северу, а ординаты — к востоку.
Сначала записывают в метрах абсциссу Х(южной линии сетки) нижней (южной) линии квадрата, в котором находятся точка А, т.е. Х(южной линии сетки) =79200,0 м. Циркулем и поперечным масштабом определяют расстояние Δх = Y(а)-Y(А) также в метрах с точностью масштаба. Полученную величину Δх=64,8 м прибавляют к абсциссе нижней (южной) линии квадрата Х(южной линии сетки) =79200,0 м и находят абсциссу точки А: Х(А) = 79200,0 + 64,8 = 79264,8 м.

Рис.4
Аналогично определяют ординату точки А: к значению ординаты западной линии сетки квадрата У(западной линии сетки) =66200,0 м прибавляют длину отрезка Δy =y(A)-y(b), равную 141,6 м, и получают Y(А) = 66200,0 + 141,6 = 66341,6 м.
Измерение длин линий
Расстояние между точками А и В измеряется циркулем, значение длины линии АВ находится по поперечному масштабу и записывается с точностью масштаба.
Определение
дирекционного угла
Дирекционным углом α называется горизонтальный угол, отсчитываемый от северного направления оси ОХ координатной сетки, по ходу часовой стрелки, до направления данной линии.
Дирекционный угол α линии АВ можно измерить с помощью транспортира. На рис. 5 представлены дирекционные углы α1, α2, α3, и α4 четырех линий М-1, М-2, М-3, М-4.

Рис.5
Дирекционным угол заданного направления α пр называется прямым , а противоположного – обратным α обр (рис. 6).

Рис.6
Связь между прямым и обратным дирекционными углами выглядит так

Румбом r называется острый горизонтальный угол между северным или южным направлением оси ОХ координатной сетки и направлением данной линии. Румбы могут иметь значения от 0 до 90 градусов и сопровождаются названием четверти, в которой находится линия. На рис. 7 показаны румбы четырех линий М-1, М-2, М-3, М-4. Румбы этих линий записывают: СВ: r1; ЮВ: r2; ЮЗ: r3; и СЗ: r4, где, например, СВ — наименование румба, а r1 — значение румба.

Рис.7
Румб заданного направления r пр называется прямым , а противоположного – обратным r обр. Прямой и обратный румбы равны по величине и отличаются только наименованием (рис. 8).
Например, если прямой румб равен r пр = СВ: 350 градусов, то обратный румб равен r обр= ЮЗ: 350 градусов.

Рис.8
Таблица перехода от дирекционных углов α к румбам r приведена ниже.
Формулы перехода от дирекционных углов к румбам

Определение отметок точек
и крутизны ската линии местности
Высотой Н точки местности называется расстояние по направлению отвесной линии от точки до уровенной поверхности.
Например, Н(А) = A(a) – высота точки А над уровенной по-верхностью PQ, Н(В) = B(b) — высота точки B над уровенной по-верхностью PQ (рис. 9).
Отметкой точки местности называется численное значение высоты точки. Например, Н(А) = 150 м, Н(В) =149 м.
На топографическом плане рельеф изображается надписями отметок отдельных характерных точек, условными знаками (промоина, обрыв и т. п.) и горизонта-лями.
Горизонталями называются замкнутые кривые линии, со-единяющие точки местности с одинаковыми отметками. Горизонтали образуются путём пересечения поверхности местности секущими горизонтальными плоскостями, проведенными через заданное расстояние, которое называется высотой сечения рельефа h.
Заложением называется расстояние d на плане между двумя соседними горизонталями (рис. 9 – 11).

Рис.9
По отметкам двух смежных (соседних) горизонталей можно определить отметку точки, лежащей между ними. Например: отметка первой точки В на нижней (рис. 10) горизонтали H1 = 161 м, отметка второй точки А на верхней (рис. 10) горизонтали H2 = 162 м (т.е. высота сечения рельефа h = 1 м), заложение d = 16,8 м, расстояние от первой горизонтали до точки С равно с = 7,6 м (рис. 10). Тогда (с требуемой точностью до 0,1 м) вычисляем отметку НС точки С по формуле


Крутизна ската — это угол, образуемый направлением ската с горизонтальной плоскостью в данной точке А. Уклон u линии местности – это тангенс угла наклона ν линии местности (тангенс крутизны ската) к горизонтальной плоскости (рис. 11).

Рис.11

Чем больше угол наклона, тем скат круче.
Для нашего примера уклон линии местности между горизонталями равен
Источник
Практическое
занятие № 1 Определение расстояний по картам с применением числового и
линейного масштабов
Цель
занятия
– научиться определять расстояний по картам с применением числового, линейного,
поперечного масштабов
Дидактическое
оснащение: карта
местности, линейка, калькулятор.
Задание:
рассчитать
длину линии на местности и длину отрезка на плане.
Краткие теоретические сведения
Масштаб – это отношение длины линии на карте, плане
(чертеже) Sp к длине горизонтального приложения соответствующей линии в
натуре (на местности) Sm.
Численный масштаб – 1/ М, правильная дробь, у которой
числитель равен 1, а знаменатель М показывает во сколько раз уменьшены линии
местности по сравнению с планом.
Например, масштаб 1:10000 означает, что все линии местности
уменьшены в 10000 раз, т.е. 1 см плана соответствует 10000 см на местности
или 1 см плана = 100 м на местности,
или 1 мм плана = 10 м на местности.
Следовательно, зная длину отрезка Sp плана по
формуле Sm=Sp*M можно вычислить длину линии на местности или по формуле Sp= Sm:M определить длину
отрезка на плане.
Например, длина линии на местности 252 м; масштаб плана
1:10000. Тогда длина линии на плане Sр=252м : 10000=0,0252м = 25,2мм.
И обратно, длина отрезка на плане равна 8,5 мм; масштаб
плана 1:5000. Требуется определить длину линии местности. Она будет 8,5 мм *
5000 = 42,5м.
Порядок
работы:
1.
Вычислите длину линии на местности Sm, длину
отрезка на плане Sp для данных, приведенных в таблице 1. Результаты запишите в
соответствующую графу таблицы.
2.
Замерить линейкой длину отрезка на плане Sp между городами, используя карту.
Определить длину линии на местности Sm для данных. Результаты запишите в
соответствующую графу таблицы.
Таблица
1
|
Масштаб |
Длина |
Длина |
Масштаб |
Длина |
Длина |
|
1:2000 |
80,4 |
1:10000 |
62,5 |
||
|
1:5000 |
380,5 |
1:25000 |
20,2 |
||
|
1:10000 |
536 |
1:5000 |
12,5 |
||
|
1:25000 |
625 |
1:50000 |
6,2 |
||
Содержание отчета: укажите номер практической работы, тему, цель, оборудование,
выполните задания методических указаний, сформулируйте и запишите вывод.
Контрольные вопросы
1. Виды масштабов, их практическое значение
для картографии.
2. Дайте понятие графические
масштабы.
Пример построения поперечного масштаба.
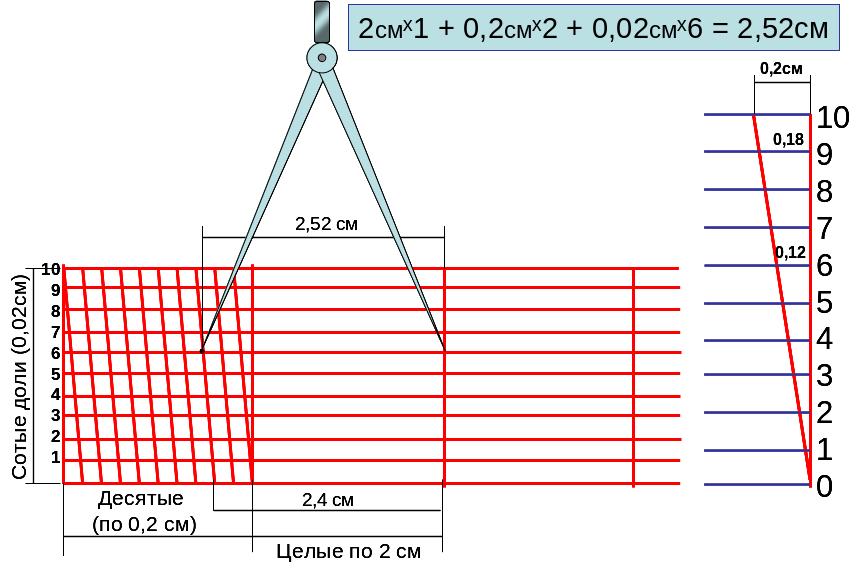
Рис.3
Точность
масштаба.
Карта
или план – это графические документы.
Принято считать, что точность графических
построений оценивается величиной 0.1
мм. Длина горизонтального проложения
линии местности, соответствующего на
карте отрезку 0.1 мм, называется точностью
масштаба. Практический смысл этого
понятия заключается в том, что детали
местности, имеющие размеры меньше
точности масштаба, на карте в масштабе
изобразить невозможно, и приходится
применять так называемые внемасштабные
условные знаки.
На
плане невооруженным глазом можно
различить две точки, если они расположены
на расстоянии 0,1 мм и более. Поэтому
величину t
= 0,1 мм х N называют точностью
масштаба плана.
Она показывает расстояние на местности,
соответствующее отрезку длиной 0,1мм
на плане.
Например,
для плана М 1 : 5 000 точность масштаб равна
t
= 0,1мм х 5000=500мм =50см =0,5м или 1см соответствует
50м на местности. 1мм – 5м, 0,1мм -0,5м.
Кроме
понятия “точность масштаба”
существует понятие “точность плана”.
Точность плана показывает, с какой
ошибкой нанесены на план или карту
точечные объекты или четкие контуры.
Точность плана оценивается в большинстве
случаев величиной 0.5 мм; в нее входят
ошибки всех процессов создания плана
или карты, в том числе и ошибки графических
построений.
Задание
-
Вычислить длину линии на местности (данные в таблице по варианту)
|
Вариант |
Sn, |
Масштаб карты |
Вариант |
Sn, |
Масштаб карты |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
12,1 |
1:1 000 |
11 |
15,1 |
1:50 000 |
|
2 |
13.1 |
1:10 000 |
12 |
1,5 |
1:100 000 |
|
3 |
5,0 |
1:5000 |
13 |
2,4 |
1:500 |
|
4 |
5,1 |
1:500 |
14 |
14,1 |
1:5 000 |
|
5 |
25,2 |
1:5 000 |
15 |
25,6 |
1:50 000 |
|
6 |
12,5 |
1:50 000 |
16 |
31,7 |
1:1 000 |
|
7 |
3,2 |
1:100 000 |
17 |
11,7 |
1:10 000 |
|
8 |
2,3 |
1:500 |
18 |
6,5 |
1:5000 |
|
9 |
13,4 |
1:5 000 |
19 |
4,7 |
1:500 |
|
10 |
6,2 |
1:50 000 |
20 |
18,6 |
1:5 000 |
2. Вычислить длину отрезка на плане (данные в таблице по варианту).
|
Вариант |
SM, |
Масштаб карты |
Вариант |
SM, |
Масштаб карты |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
2,5 |
1:50 000 |
11 |
165,2 |
1:1 000 |
|
2 |
5,0 |
1:100 000 |
12 |
945,1 |
1:10 000 |
|
3 |
125,2 |
1:500 |
13 |
2000,4 |
1:5000 |
|
4 |
730,5 |
1:5 000 |
14 |
1845,0 |
1:500 |
|
5 |
800,0 |
1:50 000 |
15 |
790,5 |
1:5 000 |
|
6 |
3,6 |
1:1 000 |
16 |
45,5 |
1:50 000 |
|
7 |
35.0 |
1:10 000 |
17 |
843,8 |
1:100 000 |
|
8 |
600,2 |
1:5000 |
18 |
891,4 |
1:500 |
|
9 |
1000,2 |
1:500 |
19 |
468,2 |
1:5 000 |
|
10 |
35,5 |
1:5 000 |
20 |
6,8 |
1:50 000 |
3. Вычислить
точность масштаба, заполнить таблицу
по форме;
-
Масштаб
1см
плана соответствуетМ
местностиТочность
масштаба, t1
2
3
Данные в таблице
по варианту
-
№ варианта
Масштаб
№ варианта
Масштаб
Все четные
варианты1:100
Все четные
варианты1:200
1:50
1:500
1:500
1:1000
~1:25000
1:2000
1:500
1:5000
1:10
0001:10000
1:25 000
1:25
0001:250 000
1:50 000
1:500 000
1: 100 000
1:
1 000 0001:200 000
4.
Построить номограмму линейного масштаба,
указать длину линии на местности,
вычислить эту же длину на плане (данные
в таблице по
варианту).
-
Вариант
Основание
масштаба, см
п
Масштаб
Sм,м
1
1,0
5
1:1000
25,0
2
2,0
5
1:10 000
540,0
3
2,0
10
1:100
7,5
4
2,0
10
1:100
0005350,0
5
1,0
5
1:1000
66
6
2,0
10
1:50
000840.0
7
1,0
5
1:200
9,6
8
2,0
10
1:200 000
6870.0
9
2,0
10
1:50000
163.0
10
2,0
5
1:50 000
2320,0
11
1,0
20
1:500
19.6
12
2,0
20
1:500 000
20720,0
13
1,0
5
1:100
9.9
14
2,0
5
1:1000
34,5
15
2,0
5
1:100 000
3340,0
16
2,0
5
1:10000
430,0
17
1,0
10
1:200
5,4
18
2,0
10
1:10
000150.3
19
2,0
10
1:50
000650.0
20
2,0
10
1:1000
37.5
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Масштабы планов и карт. Численный и линейный масштаб
Страницы работы
Содержание работы
Дисциплина:
ИНЖЕНЕРНАЯ ГЕОДЕЗИЯ
Раздел: МАСШТАБЫ ПЛАНОВ И КАРТ
Цель работы: научиться пользоваться стандартными масштабами,
строить номограммы линейного и поперечного масштабов и применять их в
геодезической практике, производить по карте измерение длин линий..
Необходимые материалы и
принадлежности: учебная карта
У-42-73-В, учебная карта У-41-144-Б, фрагменты карт комплекта №7-100,
циркуль-измеритель, линейка, карандаш.
Тема: ЧИСЛЕННЫЙ И ЛИНЕЙНЫЙ МАСШТАБ
Основные положения
Используя
значение 1/М числового масштаба и зная длину S проложения
линии на местности, можно по формуле
s=S/М
(1.1)
определить ее длину на плане
или по формуле
S=sМ
(1.2)
определить длину линии на
местности, зная длину s этого отрезка на плане.
Пример 1.
Длина отрезка S= 142 м. Найти величину изображения этого отрезка на
плане масштаба 1:2000.
По формуле (1.1) получим
s = 142 м/2000 = 0,071 м = 7,1 см.
Пример 2. На плане
масштаба 1:500 величина отрезка между двумя точками s=14,6 см. Определить длину S этой линии на
местности.
По
формуле (1.2) находим S=14,6 см x 500=7300 см =73 м.
ЗАДАНИЕ №1
Дано расстояние между двумя
точками на карте l. Определить длину
горизонтального проложения соответствующей линии местности S, если масштаб карты 1
: М равен: 1) 1 : 2000; 2) 1 : 5000; 3) 1 : 10 000; 4) 1 : 25 000 (табл.
1).
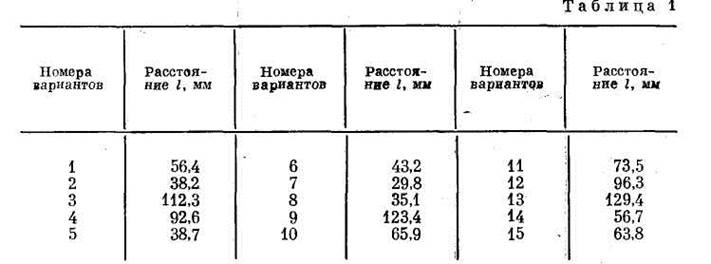
Решение. Вычисление
производится по формуле
S = lM,
где М —
знаменатель численного масштаба, показывающий, во сколько раз линии
местности уменьшены при их изображении на карте.
Например, если 1 : М
= 1 : 2000 и l = 56,4 мм, то d =56,4 мм ×2000 = 112 800 мм = 112,8 м.
ЗАДАНИЕ №2
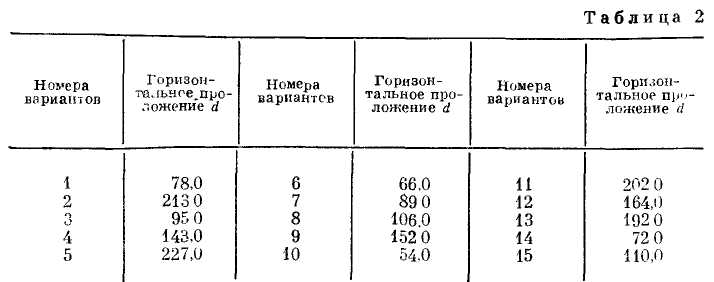
Дано горизонтальное
проложение dлиний местности. Определить с точностью 0,1 мм длину соответствующих линий на картах следующих масштабов: 1) 1 : 2000; 2) 1 : 5000;
3) 1 : 10 000 (табл. 2).
![]() Решение. Вычисления выполняют по формуле
Решение. Вычисления выполняют по формуле
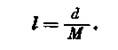
Если, например, d= 78,0 м = 78 000 мм, то I= 78 000 : 2000 = = 39,0 мм на карте масштаба 1 : 2000.
Тема: ОПРЕДЕЛЕНИЕ РАССТОЯНИЙ НА ТОПОГРАФИЧЕСКОЙ
КАРТЕ
С ПОМОЩЬЮ ЛИНЕЙНОГО И ПОПЕРЕЧНОГО МАСШТАБОВ
Рассмотрим
пример построения линейного масштаба и пользования им, если численный масштаб
равен 1 : 5000. Приняв за основание отрезок в 1 см, соответствующий 50 м на местности, откладывают его несколько раз по прямой и подписывают, как
указано на рис. 1, а. Левое основание делят на пять или десять частей.
Теперь, взяв расстояние на плане в раствор циркуля-измерителя, одну его ножку
устанавливают на штрих, разделяющий основания, но так, чтобы другая ножка
попала слева от 0 до 50.
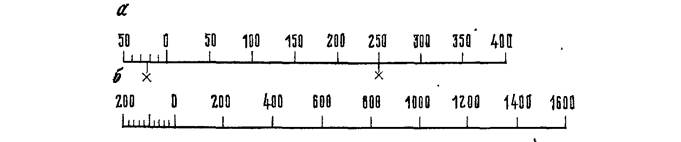
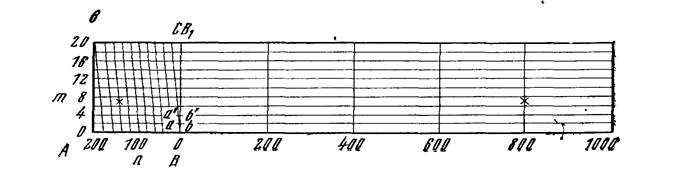
Рис. 1. Номограммы масштабов
Построение
линейного масштаба, когда знаменатель численного масштаба не выражается
круглым числом, что бывает при пользовании аэрофотоснимком местности, по
существу ничем не отличается от только что сказанного. Например, масштаб аэрофотоснимка
1 : 17 380. Согласно условиям, указанным выше, основание линейного масштаба
должно соответствовать 200 м, а длина его определится из соотношения
1 см соответствует 173,8 м, х см – 200,0 м, следовательно,
![]()
Величину
этого отрезка несколько раз откладывают на прямой, левое основание делят на
части и масштаб вычерчивают, как показано на рис. 1, б.
Так
как доли деления по линейному масштабу оценивают на глаз, что снижает точность
измерения расстояний, то пользуются поперечным масштабом (рис. 8, в),
который строят следующим образом. Выбирают основание масштаба АВ (см.
рис. 8, в), как и линейного, и откладывают его несколько раз на прямой.
Из полученных точек восставляют перпендикуляры к этой прямой (или проводят
параллельные линии, не перпендикулярные к прямой). Левое основание делят на 5
или 10 равных делений, в общем случае на п делений, а на перпендикулярах
откладывают т равных делений (тоже 5 или 10) произвольной длины, но в
целом не более 3 см. Через полученные точки на перпендикулярах проводят линии,
параллельные основанию.
Затем на левом основании
через все деления проводят линии, параллельные ВС, как показано на рис.
8, в, называемые трансверсалями. Отрезок ab
называется наименьшим делением поперечного масштаба. Величина его
зависит от длины основания АВ и числа делений п . Из подобия
треугольников ВСВ1 и Ваb следует,
что
![]()
откуда
![]()
![]()
поэтому
![]()
т. е. наименьшее деление поперечного масштаба равно
основанию, деленному на произведение чисел п и т.
Для масштаба 1 : 10 000, изображенного на рис. 1, в,
основание АВ, равное 2 см, соответствует 200 м на местности. Число делений п = 10 и m = 10, поэтому
наименьшее деление поперечного масштаба соответствует ab =200/(10х10) = 2 м на местности.



