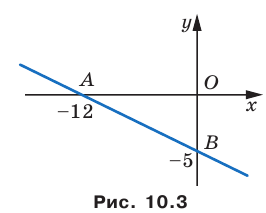
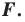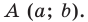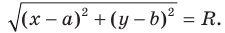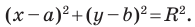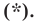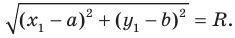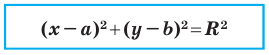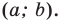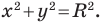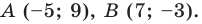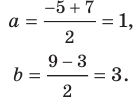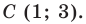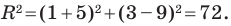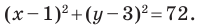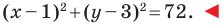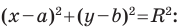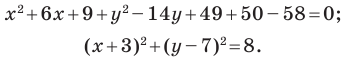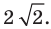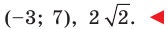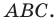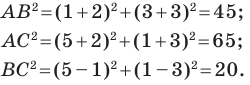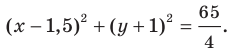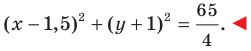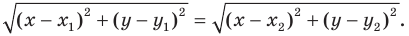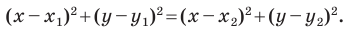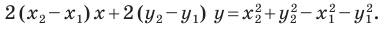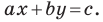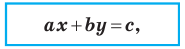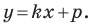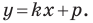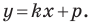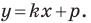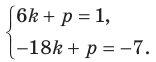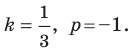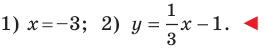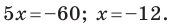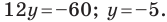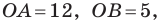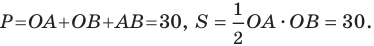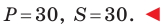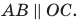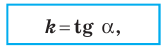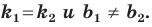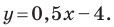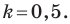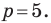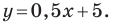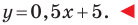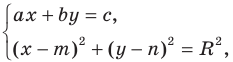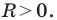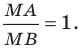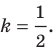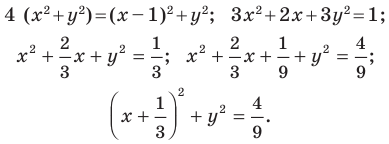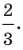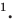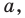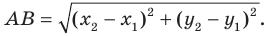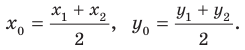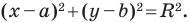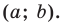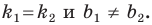Длина отрезка. Существует целая группа заданий (входящих в экзаменационные типы задач), связанная с координатной плоскостью. Это задачи начиная с самых элементарных, которые решаются устно (определение ординаты или абсциссы заданной точки, либо точки симметричной заданной и другие), заканчивая задачами в которых требуется качественное знание, понимание и хорошие навыки (задачи связанные с угловым коэффициентом прямой).
Постепенно мы с вами рассмотрим все их. В этой статье начнём с элементарных. Это простые задачи на определение: абсциссы и ординаты точки, длинны отрезка, середины отрезка, синуса или косинуса угла наклона прямой. Большинству эти задания будут не интересны. Но изложить их считаю необходимым.
Дело в том, что не все учатся в школе. Очень многие сдают ЕГЭ спустя 3-4 и более лет после её окончания и что такое абсцисса и ордината помнят смутно. Будем разбирать и другие задачи, связанные с координатной плоскостью, не пропустите, подпишитесь, на обновление блога. Теперь немного теории.
Построим на координатной плоскости точку А с координатами х= 6, y=3.
Говорят, что абсцисса точки А равна шести, ордината точки А равна трём.
Если выразиться просто, то ось ох это ось абсцисс, ось оу это ость ординат.
То есть, абсцисса это точка на оси ох в которую проецируется точка заданная на координатной плоскости; ордината это точка на оси оу в которую проецируется оговоренная точка.
Длина отрезка на координатной плоскости
Формула для определения длины отрезка, если известны координаты его концов:
Как вы видите, длина отрезка — это длина гипотенузы в прямоугольными треугольнике с катетами равными
ХВ – ХА и УВ – УА
* * *
Середина отрезка. Её Координаты.
Формула для нахождения координат середины отрезка:
Уравнение прямой проходящей через две данные точки
Формула уравнения прямой походящей через две данные точки имеет вид:
где (х1;у1) и (х2;у2) координаты заданных точек.
Подставив значения координат в формулу, она приводится к виду:
y = kx + b, где k — это угловой коэффициент прямой
Эта информация нам понадобиться при решении другой группы задач связанных с координатной плоскостью. Статья об этом будет, не пропустите!
Что ещё можно добавить?
Угол наклона прямой (или отрезка) это угол между осью оХ и этой прямой, лежит в пределах от 0 до 180 градусов.
Рассмотрим задачи.
Из точки (6;8) опущен перпендикуляр на ось ординат. Найдите ординату основания перпендикуляра.
Основание перпендикуляра опущенного на ось ординат будет иметь координаты (0;8). Ордината равна восьми.
Ответ: 8
Найдите расстояние от точки A с координатами (6;8) до оси ординат.
Расстояние от точки А до оси ординат равно абсциссе точки А.
Ответ: 6.
Найдите ординату точки, симметричной точке A(6;8) относительно оси Ox.
Точка симметричная точке А относительно оси оХ имеет координаты (6;– 8).
Ордината равна минус восьми.
Ответ: – 8
Найдите ординату точки, симметричной точке A(6;8) относительно начала координат.
Точка симметричная точке А относительно начала координат имеет координаты (– 6;– 8).
Её ордината равна – 8.
Ответ: –8
Найдите абсциссу середины отрезка, соединяющего точки O (0;0) и A(6;8).
Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (0;0) и (6;8).
Вычисляем по формуле:
Получили (3;4). Абсцисса равна трём.
Ответ: 3
*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку. Середину отрезка несложно будет определить по клеткам.
Найдите абсциссу середины отрезка, соединяющего точки A(6;8) и B(–2;2).
Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (–2;2) и (6;8).
Вычисляем по формуле:
Получили (2;5). Абсцисса равна двум.
Ответ: 2
*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку.
Найдите длину отрезка, соединяющего точки (0;0) и (6;8).
Длина отрезка при данных координатах его концов вычисляется по формуле:
в нашем случае имеем О(0;0) и А(6;8). Значит,
*Порядок координат при вычитании не имеет значения. Можно из абсциссы и ординаты точки О вычесть абсциссу и ординату точки А:
Ответ:10
Найдите косинус угла наклона отрезка, соединяющего точки O (0;0) и A (6;8), с осью абсцисс.
Угол наклона отрезка – это угол между этим отрезком и осью оХ.
Из точки А опустим перпендикуляр на ось оХ:
То есть, угол наклона отрезка это угол ВОА в прямоугольном треугольнике АВО.
Косинусом острого угла в прямоугольном треугольнике является
отношение прилежащего катета к гипотенузе
Необходимо найти гипотенузу ОА.
По теореме Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Таким образом, косинус угла наклона равен 0,6
Ответ: 0,6
Из точки (6;8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра.
Посмотреть решение
Через точку (6;8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью оУ.
Посмотреть решение
Найдите расстояние от точки A с координатами (6;8) до оси абсцисс.
Посмотреть решение
Найдите расстояние от точки A с координатами (6;8) до начала координат.
Посмотреть решение
Найдите абсциссу точки, симметричной точке A(6,8) относительно оси оУ.
Посмотреть решение
Найдите абсциссу точки, симметричной точке A(6,8) относительно начала координат.
Посмотреть решение
Найдите ординату середины отрезка, соединяющего точки O (0;0) и A (6;8).
Посмотреть решение
Найдите ординату середины отрезка, соединяющего точки A (6;8) и B (-2;2).
Посмотреть решение
Найдите ординату точки пересечения оси оУ и отрезка, соединяющего точки A (6;8) и B (- 6;0).
Посмотреть решение
Найдите длину отрезка, соединяющего точки А(6;8) и В(-2;2).
Посмотреть решение
Найдите синус угла наклона отрезка, соединяющего точки O (0;0) и A (6;8), с осью абсцисс.
Посмотреть решение
Это даже не задача, а вопрос.
Частенько Александр Васильевич Суворов, встречая любого подчинённого, который случайно попадался ему на глаза задавал вопрос, порой неожиданный. Однажды спросил офицера своей армии:”Сколько вёрст до луны?”. Что тот ответил?
Первый, кто даст правильный ответ получит поощрительный приз — 100 рублей. Ответы пишите в комментариях.
На этом всё. Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
ось u, если даны его длина d и угол j наклона к оси:
/3;
/3;
/2;
;
/3.
чертеже отрезки, исходящие из начала координат,
зная их проекции на координатные оси:
чертеже отрезки, имеющие началом точку M(2; -1), зная
их проекции на координатные оси:
4), М5(0; -3). Найти проекции на координатные оси
следующих отрезков:
отрезка
что его начало в точке М1(-2; 3), найти координаты его конца.
отрезка
что его конец в точке B(1; -3), найти координаты его
начала.
чертеже отрезки, исходящие оиз начала координат,
зная длину d и полярный угол q каждого из них:
/6;
/3;
/3.
чертеже отрезки, имеющие началом точку М(2; 3), зная
длину и полярный угол каждого из них (координаты
точки М декартовы):
/9;
/2ж
на координатные оси отрезков, зная длину d и
полярный угол q каждого из них:
/6;
/4.
отрезков на координатные оси. Вычислить длину
каждого из них.
отрезков на координатные оси. Вычислить длину d и
полярный угол q каждого из них.
Y=
Y=2.
8). Вычислить длину и полярный
угол слдующих отрезков:
равна 5, его проекция на ось абсцисс равна 4. Найти
проекцию этого отрезка на ось ординат при
условии, что он образует с осью ординат:
проекция на ось абсцисс равна –12. Найти
координаты конца этого отрезка при условии, что
он образует с осью ординат:
проекция на ось ординат равна 15. Найти координаты
начала этого отрезка при условии, что он образует
с осью абсцисс:
его проекцию на ось, которая составляет с осью Ox
угол q =2p /3.
проекцию отрезка
с осью Ox угол q =-p
/6.
Q(3; 1). Найти проекцию отрезка
ось, которая составляет с осью Ox угол
проекцию отрезка
точки A(5; -4), B(-7; 1) и направленную:
-4), C(-3; 4), D(-2; 2), E(10; -3). Определить расстояние d между
точками:
вершины квадрата A(3; -7) и В(-1; 4). Вычислить его
площадь.
противоположные вершины квадрата P(3; 5), Q(1; -3).
Вычислить его площадь.
правильного треугольника, две вершины которого
суть A(-3; 2), B(1; 6).
-7), В(5; -7), С(-2; 5) параллелограмма ABCD, четвертая
вершина которого D противоположна B. Определить
длины диагоналей того параллелограмма.
суть точки P(4; 9), Q(-2; 1). Вычислить площадь этого
ромба.
суть точки P(3; -4), Q(1; 2). Вычислить длину высоты
этого ромба.
А(3; -5), В(-2; -7), С(18; 1) лежат на одной прямой.
треугольник с вершинами A1(1; 1), A2(2;
3), A3(5; -1) прямоугольный.
А(2; 2), В(-1; 6), С(-5; 3), D(-2; -1) являются вершинами
квадрата.
среди внутренних углов треугольника с вершинами
M1(1; 1), M2(0; 2), M3(2; -1) тупой угол.
внутренние углы треугольника с вершинами M(-1; 3),
N(1; 2), P(0, 4) острые.
треугольника суть точки A(5; 0), B(0; 1), C(3; 3). Вычислить
его внутренние углы.
треугольника суть точки А(
его внешний угол при вершине А.
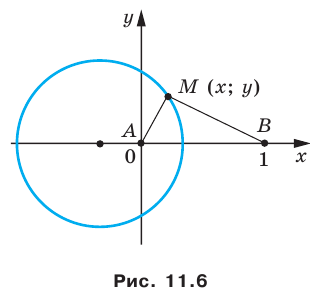
найти такую точку М, расстояние от которой до
точки N(2; -3) равнялось бы 5.
найти такую точку М, расстояние от которой до
точки N(-8; 13 равнялось бы 17.
N(5; -2); на оси абсцисс найти такую точку Р, чтобы
угол MPN был прямым.
проведена окружность, касающаяся обеих
координатных осей. Определить ее центр С и радиус
R.
окружность радиуса 5, касающаяся оси Ox.
Определить центр С окружности.
координаты точки М2, симметричной точке М1(1; 2) относительно прямой, проходящей
через точки А(1; 0), В(-1; -2).
противоположные вершины квадрата А(3; 0) и С(-4; 1).
Найти две его другие вершины.
веришны квадрата А(2; -1) и В(-1; 3). Определить две его
другие вершины.
треугольника M1(-3; 6), M2(9;
-10), M3(-5; 4). Определить центр
С и радиус R круга, описанного около этого
треугольника.
Чтобы найти на плоскости какой-то объект, его описывают двумя значениями. Так каждое место в зале кинотеатра имеет два параметра: ряд и место. Каждая клетка на шахматной доске или при игре в «морской бой» описывается номером строки и буквой, обозначающей столбец.
В математике определение местоположения объекта на плоскости придумали быстро находить с помощью системы координат, образованной двумя прямыми, называемых координатными осями (или осями координат).
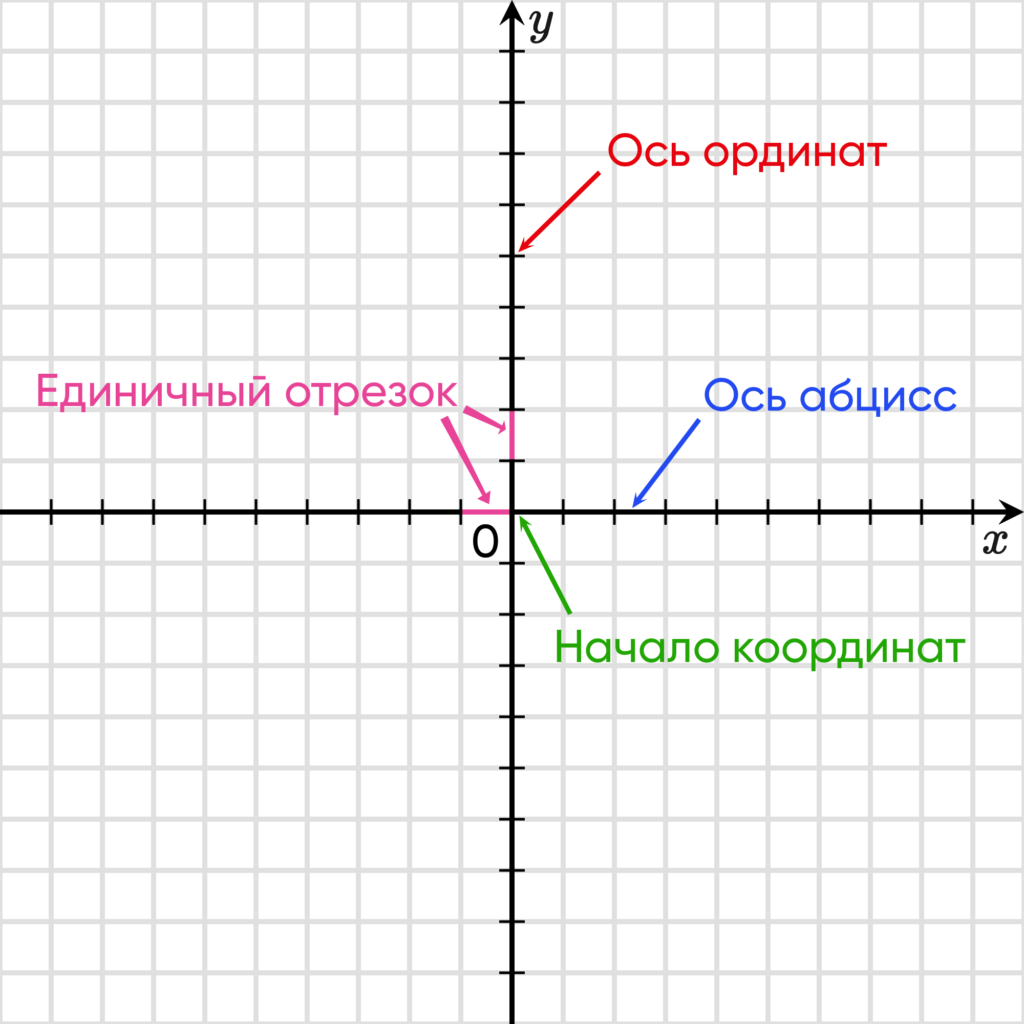
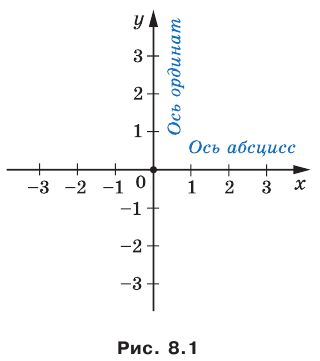
Абсцисса, ордината, начало координат и единичный отрезок
Эти оси имеют общепринятые наименования. А именно, горизонтальную ось именуют осью абсцисс и на письме обозначают $Оx$
Вертикальную ось называют осью ординат и на письме обозначают $Оy$
Оси пересекаются под прямым углом перпендикулярно друг к другу, поэтому такая система координат и называется прямоугольной.
Место пересечения осей координат является началом отсчета. Обычно эту точку обозначают буквой $О$ и называют началом координат. Ее называют еще иногда нулевой точкой.
На каждой оси выбирается единичный отрезок, с помощью которого вычисляются координаты объекта. Длиной единичного отрезка может выступать любая единица измерения, но она должна быть одинаковой на каждой из осей. То есть, если единичный отрезок на оси абсцисс задан, например, равным 1 см, то и на оси ординат единичный отрезок тоже должен быть равен одному сантиметру.
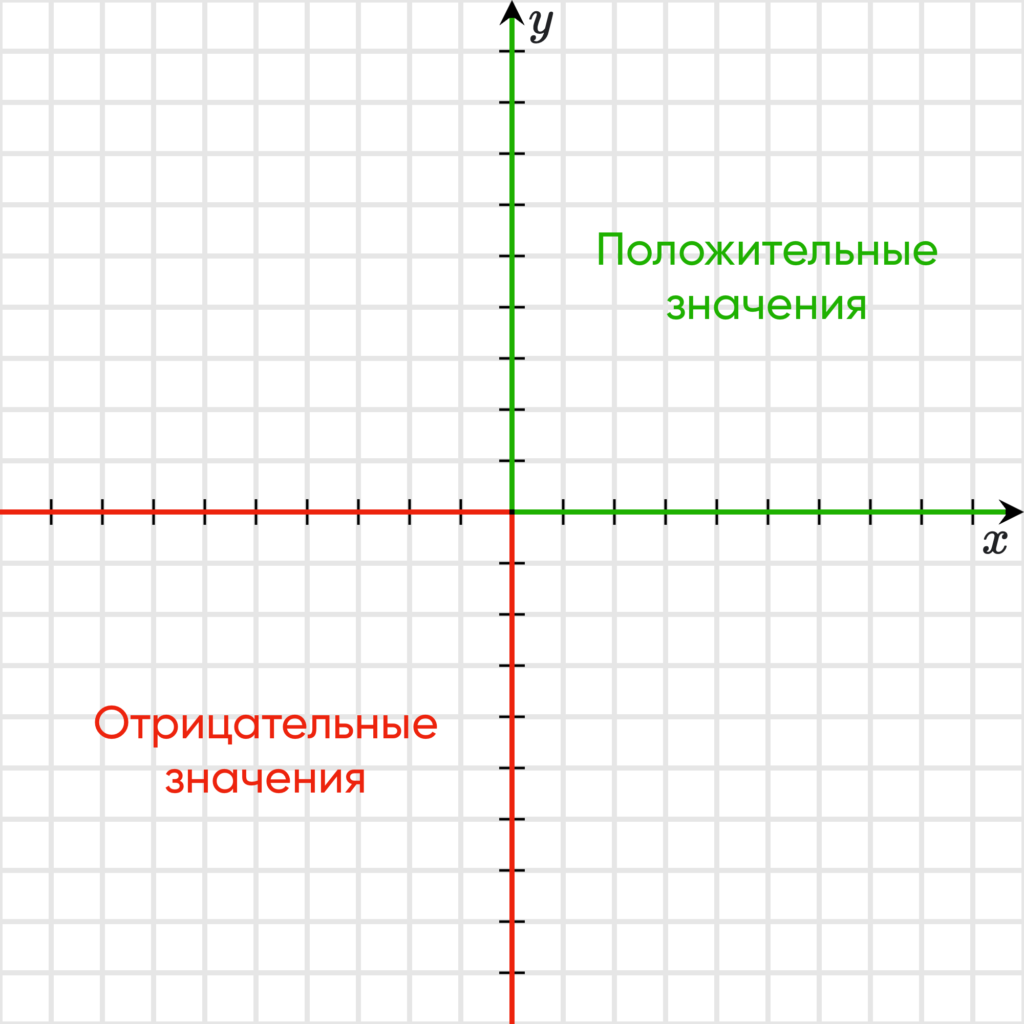
Положительное и отрицательное направление
У осей стрелкой задается положительное направление:
- так обычно у оси $Оx$ положительным считается направление вправо;
- у оси $Оy$ положительным считается направление снизу вверх.
В таком случае часть прямой $Оx$ левее точки $О$ будет принимать отрицательные значения. Аналогично часть прямой $Оy$ ниже точки отсчета $О$ будет также принимать отрицательные значения.
Таким образом, все вместе:
- начало координат $О$
- пересекающиеся под прямым углом оси $Оx$ и $Оy$ с заданными направлениями
- заданный единичный отрезок
образуют в математике прямоугольную систему координат, плоскость называют координатной.
Или другими словами:
Прямоугольная система координат – это две взаимно перпендикулярные координатные оси с заданными направлениями, единицей длины и точкой отсчета в месте их пересечения.
На письме система координат обозначается $Оxy$
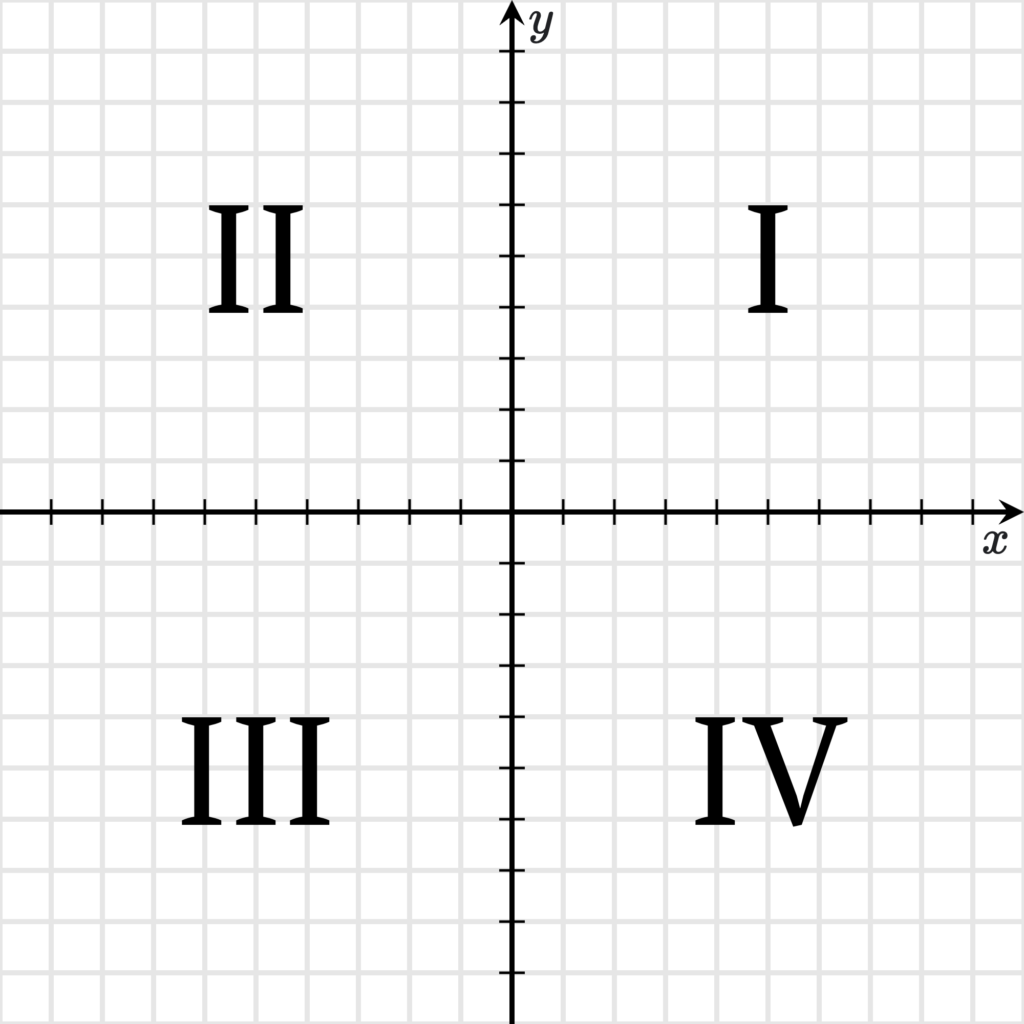
Четверти
Осями координат плоскость делится на 4 части, их обозначают римскими цифрами. Каждая часть называется «квадрант». Другие названия: «координатный угол» или «четверть». Нумерация четвертей принята против часовой стрелки в том порядке, в котором указано на рисунке ниже.
В квадранте I значения $x$ и $y$ будут положительными. Отсюда следует, что если координаты объекта $x$ и $y$ – числа положительные, то он находится в I квадранте.
В квадранте II значение $y$ будет положительными, а $x$ отрицательным.
В квадранте III обе координаты $x$ и $y$ будут иметь отрицательные значения.
В последнем IV квадранте значение $x$ будет положительным, а $y$ отрицательным.
Немного из истории
В латинском языке слово «координаты» получилось из двух других: co – «совместно» и ordinatus – «определенный», «упорядоченный».
Впервые необходимость нахождения координат объектов возникла в географии и астрономии. Для этого использовали широту и долготу, определяющие расположение точки на небесной сфере или на поверхности земного шара.
Таким образом начали вычислять координаты точек еще в 14 веке. Но упорядочил и систематизировал все знания в 17 веке французский математик по имени Рене Декарт. Поэтому прямоугольную систему координат также называют еще и «декартовой».
Содержание:
Декартовы координаты на плоскости:
Изучая материал этой лекции, вы расширите свои знания о координатной плоскости.
Вы научитесь находить длину отрезка и координаты его середины, зная координаты его концов.
Сформируете представление об уравнении фигуры, выведете уравнения прямой и окружности.
Ознакомитесь с методом координат, позволяющим решать геометрические задачи средствами алгебры.
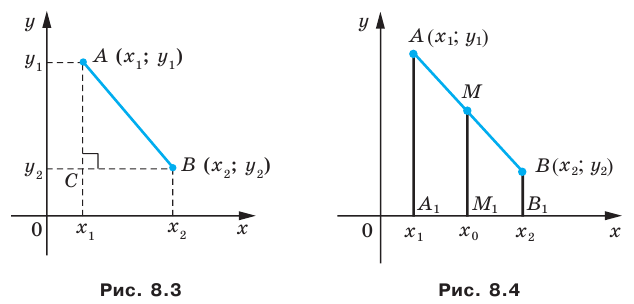
Расстояние между двумя точками с заданными координатами. Координаты середины отрезка
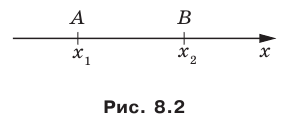
В 6 классе вы ознакомились с координатной плоскостью, то есть с плоскостью, на которой изображены две перпендикулярные координатные прямые (ось абсцисс и ось ординат) с общим началом отсчета (рис. 8.1). Вы умеете отмечать на ней точки по их координатам и наоборот, находить координаты точки, отмеченной на координатной плоскости.
Договорились координатную плоскость с осью
Координаты точки на плоскости 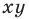
Вы знаете, как находить расстояние в между двумя точками, заданными своими координатами на координатной прямой. Для точек 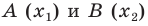
Научимся находить расстояние между точками 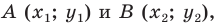
Рассмотрим случай, когда отрезок 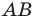
Через точки 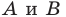
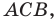
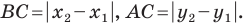
Тогда формулу расстояния между точками 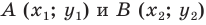
Докажите самостоятельно, что эта формула остается верной и для случая, когда отрезок 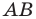
Пусть 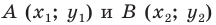
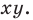
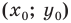
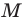
Рассмотрим случай, когда отрезок 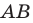
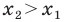
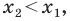
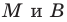
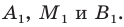
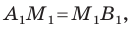
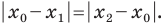
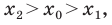
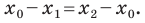

Формулы для нахождения координат середины отрезка остаются верными и для случая, когда отрезок 
Пример №1
Докажите, что треугольник с вершинами в точках 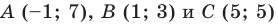
Решение:
Используя формулу расстояния между двумя точками, найдем стороны данного треугольника:
Следовательно, 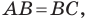
Поскольку 
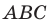
Пример №2
Точка 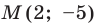
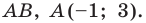
Решение:
Обозначим 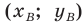
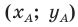
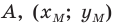
Поскольку 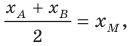
Аналогично
Ответ:
Пример №3
Докажите, что четырехугольник 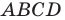
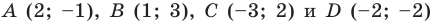
Решение:
Пусть точка 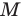
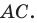
Следовательно,
Пусть точка 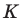
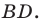
Следовательно,
Таким образом, точки 
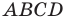
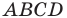
Найдем диагонали параллелограмма:
Следовательно, диагонали параллелограмма 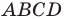
Уравнение фигуры. Уравнение окружности
Из курса алгебры 7 класса вы знаете, какую фигуру называют графиком уравнения. В этом пункте вы ознакомитесь с понятием уравнения фигуры.
Координаты 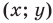
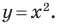
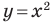
Определение. Уравнением фигуры 
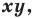
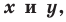
- если точка принадлежит фигуре
то ее координаты являются решением данного уравнения;
- любое решение
данного уравнения является координатами точки, принадлежащей фигуре
Например, уравнение прямой, изображенной на рисунке 9.2, имеет вид 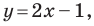
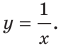
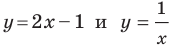
Если данное уравнение является уравнением фигуры 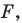
Пользуясь этими соображениями, выведем уравнение окружности радиуса 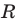
Пусть 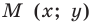
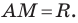
Отсюда
Мы показали, что координаты 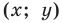
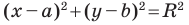
Пусть пара чисел 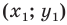
Тогда 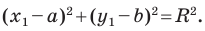
Это равенство показывает, что точка 
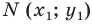
Итак, мы доказали следующую теорему.
Теорема 9.1. Уравнение окружности радиуса 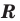
Верно и такое утверждение: любое уравнение вида 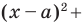
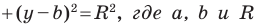
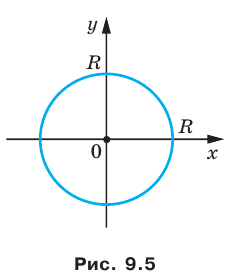
Если центром окружности является начало координат (рис. 9.5), то 
Пример №4
Составьте уравнение окружности, диаметром которой является отрезок 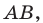
Решение:
Поскольку центр окружности является серединой диаметра, то можем найти координаты 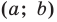
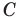
Следовательно,
Радиус окружности 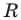
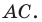
Следовательно, искомое уравнение имеет вид
Ответ:
Пример №5
Докажите, что уравнение 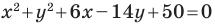
Решение:
Представим данное уравнение в виде
Следовательно, данное уравнение является уравнением окружности с центром в точке 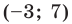
Ответ:
Пример №6
Докажите, что треугольник с вершинами в точках 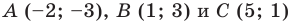
Решение:
Найдем квадраты сторон данного треугольника:
Поскольку 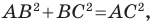
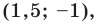
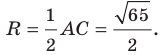
Ответ:
Уравнение прямой
В предыдущем пункте, рассматривая окружность как ГМТ, равноудаленных от данной точки, мы вывели ее уравнение. Для того чтобы вывести уравнение прямой, рассмотрим ее как ГМТ, равноудаленных от двух данных точек.
Пусть 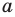
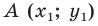
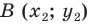
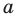
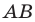
Пусть 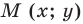
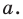
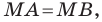
Мы показали, что координаты 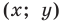
Теперь покажем, что любое решение уравнения 
Пусть 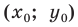
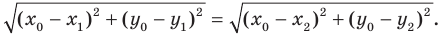
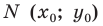
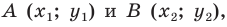
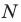
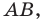
Итак, мы доказали, что уравнение 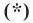
Однако из курса алгебры 7 класса вы знаете, что уравнение прямой выглядит гораздо проще, а именно: 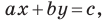
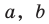
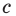
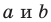
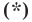
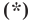
Раскроем скобки и приведем подобные слагаемые. Получим:
Обозначив 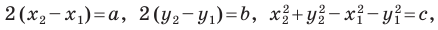
Поскольку точки 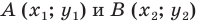
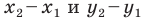
Итак, мы доказали следующую теорему.
Теорема 10.1. Уравнение прямой имеет вид?
где 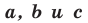
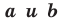
Верно и такое утверждение: любое уравнение вида 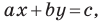
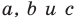
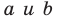
Если 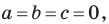
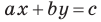
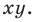
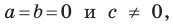
Из курса алгебры 7 класса вы знаете, что уравнение вида 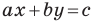
на уроках алгебры в 7 классе мы приняли без доказательства тот факт, что графиком линейной функции 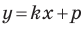
Перепишем уравнение 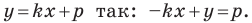
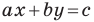
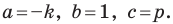
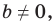
А любую ли прямую на плоскости можно задать уравнением вида 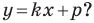
Дело в том, что прямая, перпендикулярная оси абсцисс, не может являться графиком функции, а следовательно, не может быть задана уравнением вида
Вместе с тем, если в уравнении прямой 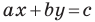
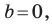
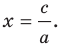
Если 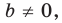
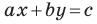
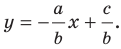
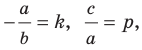
Следовательно, если 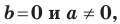
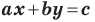
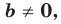
Уравнение невертикальной прямой удобно записывать в виде
Данная таблица подытоживает материал, рассмотренный в этом пункте.
Пример №7
Составьте уравнение прямой, проходящей через точки:
Решение:
1) Поскольку данные точки имеют равные абсциссы, то прямая 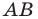
2) Поскольку данные точки имеют разные абсциссы, то прямая 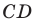
Подставив координаты точек 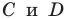
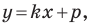
Решив эту систему уравнений, находим, что
Ответ:
Пример №8
Найдите периметр и площадь треугольника, ограниченного прямой 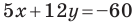
Решение:
Найдем точки пересечения данной прямой с осями координат.
С осью абсцисс: при 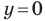
С осью ординат: при 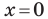
Следовательно, данная прямая и оси координат ограничивают прямоугольный треугольник 
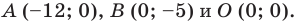
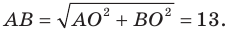
Ответ:
Угловой коэффициент прямой
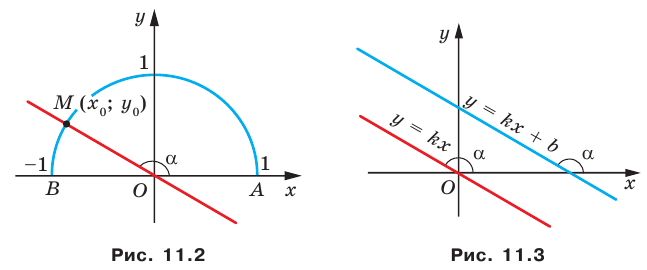
Рассмотрим уравнение 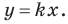
Покажем, что прямые 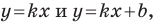
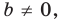
Точки 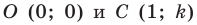
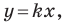
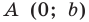
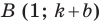
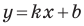
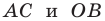
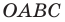
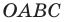
Теперь мы можем сделать такой вывод: если 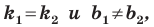
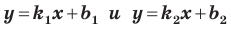
Пусть прямая 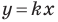
Если прямая 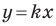
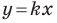
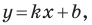
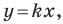
Рассмотрим прямую 
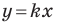
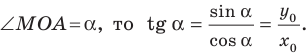
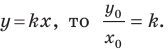
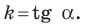
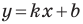
где 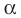
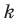
Если невертикальные прямые параллельны, то они образуют равные углы с положительным направлением оси абсцисс. Тогда тангенсы этих углов равны, следовательно, равны и их угловые коэффициенты. Таким образом,
если прямые 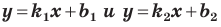
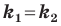
Выводы (1) и (2) объединим в одну теорему.
Теорема 11.1. Прямые 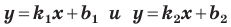
Пример №9
Составьте уравнение прямой, которая проходит через точку 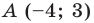
Решение:
Пусть уравнение искомой прямой 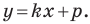
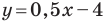
Следовательно, искомое уравнение имеет вид 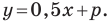
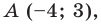
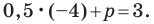
Искомое уравнение имеет вид
Ответ:
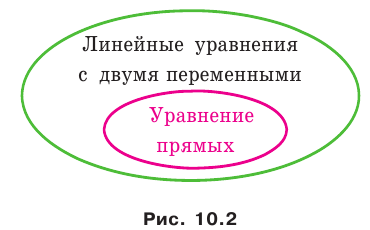
Метод координат
Мы часто говорим: прямая 
Проиллюстрируем сказанное на таком примере.
Из наглядных соображений очевидно, что прямая и окружность имеют не более двух общих точек. Однако это утверждение не является аксиомой, поэтому его надо доказывать.
Эта задача сводится к исследованию количества решений системы уравнений
где числа 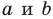
Решая эту систему методом подстановки, мы получим квадратное уравнение, которое может иметь два решения, одно решение или вообще не иметь решений. Следовательно, для данной системы существует три возможных случая:
- система имеет два решения — прямая и окружность пересекаются в двух точках;
- система имеет одно решение — прямая касается окружности;
- система не имеет решений — прямая и окружность не имеют общих точек.
С каждым из этих случаев вы встречались, решая задачи 10.17-10.19.
Метод координат особенно эффективен в тех случаях, когда требуется найти фигуру, все точки которой обладают некоторым свойством, то есть найти геометрическое место точек.
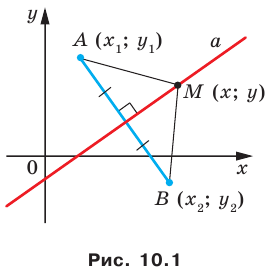
Отметим на плоскости две точки 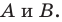
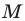
Это серединный перпендикуляр отрезка 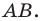
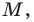
Плоскость, на которой отмечены точки 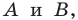
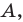
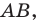
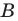
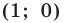
Пусть 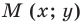
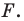
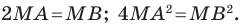
Следовательно, если точка 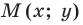
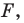
Пусть 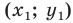
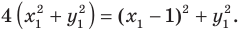
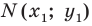
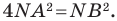
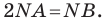
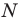
Таким образом, уравнением фигуры 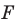
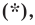
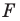
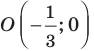
Мы решили задачу для частного случая, когда 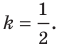
Как строили мост между геометрией и алгеброй
Идея координат зародилась очень давно. Ведь еще в старину люди изучали Землю, наблюдали звезды, а по результатам своих исследований составляли карты, схемы.
Во II в. до н. э. древнегреческий ученый Гиппарх впервые использовал идею координат для определения места расположения объектов на поверхности Земли.
Только в XIV в. французский ученый Николя Орем (ок. 1323-1382) впервые применил в математике идею Гиппарха: он разбил плоскость на клетки (как разбита страница вашей тетради) и стал задавать положение точек широтой и долготой.
Однако огромные возможности применения этой идеи были раскрыты лишь в XVII в. в работах выдающихся французских математиков Пьера Ферма и Рене Декарта. В своих трудах эти ученые показали, как благодаря системе координат можно переходить от точек к числам, от линий к уравнениям, от геометрии к алгебре.
Несмотря на то что П. Ферма опубликовал свою роботу на год раньше Р. Декарта, систему координат, которой мы сегодня пользуемся, называют декартовой. Р. Декарт в своей работе «Рассуждение о методе» предложил новую удобную буквенную символику, которой с незначительными изменениями мы пользуемся и сегодня. Вслед за Декартом мы обозначаем переменные последними буквами латинского алфавита 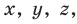
Справочный материал
Расстояние между двумя точками
Расстояние между точками 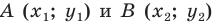
Координаты середины отрезка
Координаты 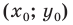
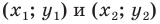
Уравнение фигуры
Уравнением фигуры 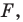
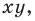
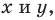
1) если точка принадлежит фигуре 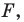
2) любое решение 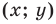
Уравнение окружности
Уравнение окружности радиуса 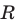
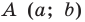
Любое уравнение вида 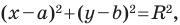
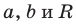
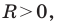
Уравнение прямой
Уравнение прямой имеет вид 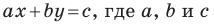
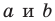
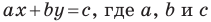
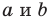
Если 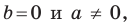
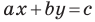
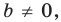
Угловой коэффициент прямой
Коэффициент 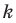
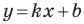
Необходимое и достаточное условие параллельности невертикальных прямых
Прямые 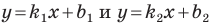
- Декартовы координаты в пространстве
- Геометрические преобразования в геометрии
- Планиметрия – формулы, определение и вычисление
- Стереометрия – формулы, определение и вычисление
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование
Геометрия,
вопрос задал tillaevmatakubzon7,
5 лет назад
Ответы на вопрос
Ответил marty70
0
Ответ:
8щулклкщкащвдвдадчззцждудвщвщь2лузвдуьдйзыьа клудутщв удалуьудудыжубткылудвьтвыьуддулуя
Предыдущий вопрос
Следующий вопрос
Новые вопросы
Химия,
9 месяцев назад
у пробірку налийте 2мл розчину натрій карбонату та долийте 2мл нітратної кислоти …
Английский язык,
9 месяцев назад
1 задание
Составьте вопросы из следующих утверждений
1)There is a swimming pool.
1)___________________________________
2)There are five books on the table.
Литература,
5 лет назад
Война и мир.
Расскажите 1)Сватовство Денисова к Наташе
2) Долохова к Соне…
Алгебра,
5 лет назад
Срочно!!!100 баллов!!
Решите 58 номер.
География,
6 лет назад
Чем отличаются природные зоны суши от природных зон в горах?
Литература,
6 лет назад
прочитайте поработайте в парах образуйте От данных корней однокоренные слова хлеба вход в море лед час свет…


































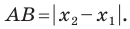
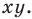
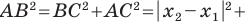
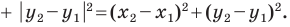

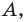
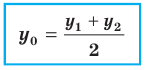
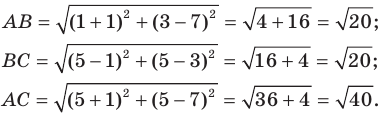

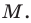
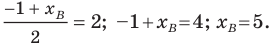
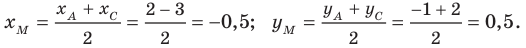
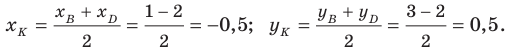
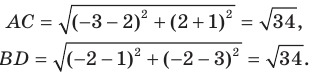

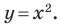
 то ее координаты являются решением данного уравнения;
то ее координаты являются решением данного уравнения;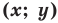 данного уравнения является координатами точки, принадлежащей фигуре
данного уравнения является координатами точки, принадлежащей фигуре