0 голосов
458 просмотров
Чему равна длина отрезка, отсекаемого прямой 7x+15y-21=0 на оси Ox?
- равна
- длина
- отрезка
- отсекаемого
- 10 – 11 классы
- алгебра
Алгебра
Miska156_zn
19 Март, 18
|
458 просмотров
0
отсекаемого прямой от нуля?
оставил комментарий
аноним
19 Март, 18
0
я написала полное условие. Видимо от нуля до прямой
оставил комментарий
Miska156_zn
19 Март, 18
Дано ответов: 2
0 голосов
Правильный ответ
Решение на фото, рисунок-схематический
RepetitorUFA_zn
19 Март, 18
0 голосов
Длина отрезка от нуля до точки пересечения с осью х равна абциссе точки пересечения. Ордината ее равна 0. Находим х
7x+15*0-21=0
7x=21
x=21:7=3
Ответ: 3
аноним
19 Март, 18
Условие
Запишите уравнение прямой, проходящей через точку M0(12,−16) параллельно прямой y=12x−15.
В ответ введите длину отрезка, отсекаемого найденной прямой от оси OY.
математика колледж
183
Решение
★
y=[b]12[/b]x−15 – уравнение прямой с угловым коэффициентом k=[b]12[/b]
Параллельные прямые имеют одинаковые угловые коэффициенты.
Общий вид прямых параллельных прямой y=[b]12[/b]x−15 :
y=[b]12[/b]x + b
Чтобы найти уравнение прямой, проходящей через точку М_(o) подставляем координаты точки M_(o) в общее уравнение
-16=[b]12[/b]*1,2 + b
Тогда
b=-30,4
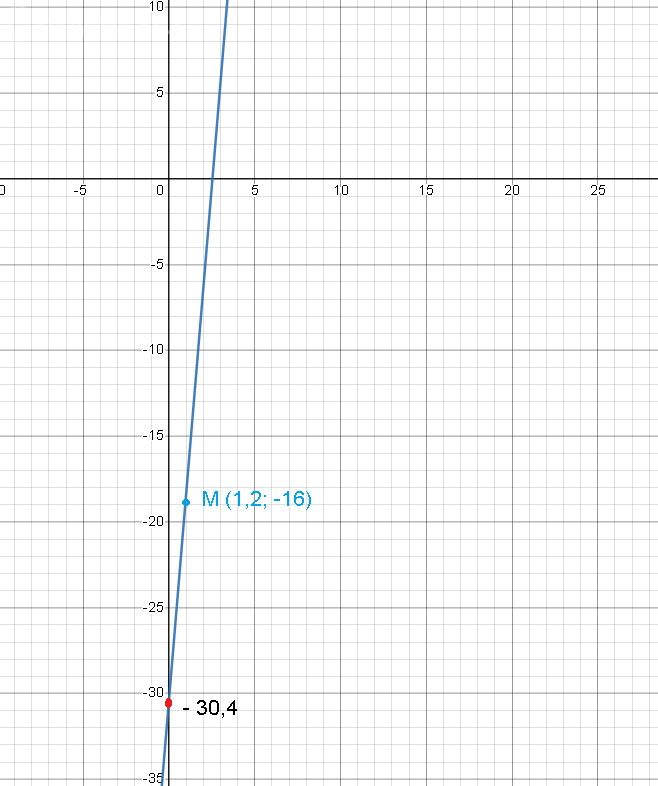
y=[b]12[/b]x -30,4 – уравнение прямой, проходящей через точку М_(o) и параллельной данной прямой y=[b]12[/b]x−15
О т в е т.
длина отрезка, отсекаемого найденной прямой от оси Oy равна |-30,4|=30,4
Написать комментарий
Чему равна длина отрезка, отсекаемого прямой 7x + 15y – 21 = 0 на оси Ox?
Вы зашли на страницу вопроса Чему равна длина отрезка, отсекаемого прямой 7x + 15y – 21 = 0 на оси Ox?, который относится к
категории Алгебра. По уровню сложности вопрос соответствует учебной
программе для учащихся 10 – 11 классов. В этой же категории вы найдете ответ
и на другие, похожие вопросы по теме, найти который можно с помощью
автоматической системы «умный поиск». Интересную информацию можно найти в
комментариях-ответах пользователей, с которыми есть обратная связь для
обсуждения темы. Если предложенные варианты ответов не удовлетворяют,
создайте свой вариант запроса в верхней строке.
-
- 0
-
-
- 0
-
Решение задания приложено
-
Комментариев (0)
По данному уравнению прямой 1 определить величины отрезков отсекаемых прямой 1 на осях координат
Общее уравнение прямой 4x – 3y + 12 = 0 представить в виде: 1) с угловым коэффициентом; 2) в отрезках на осях и 3) в нормальном виде. Построить эту прямую.
1) Уравнение прямой с угловым коэффициентом имеет вид y = kx + b. Чтобы заданное уравнение преобразовать к этому виду, разрешим его относительно y: 3y = 4x + 12, .
Сравнивая с уравнением y = kx + b, видим, что здесь угловой коэффициент прямой , а величина отрезка, отсекаемого прямой на оси ординат, b = 4 (если уравнение прямой дано в общем виде Ax + By + C = 0, то ее угловой коэффициент легко получить, если разделить коэффициент при x на коэффициент при y и взять полученное частное с обратным знаком ).
2) В отрезках на осях уравнение прямой имеет вид
(1)
Чтобы определить величины отрезков, отсекаемых заданной прямой 4x – 3y + 12 = 0, поступим так: в уравнении прямой положим y = 0. Получаем 4x + 12 = 0, а x = -3. Значит, наша прямая пересекает ось Ox в точке с координатами (-3, 0) и в уравнении (1) величина отрезка a = -3.
Полагая в нашем уравнении x = 0, определим ординату точки пересечения прямой с осью ординат. Будем иметь
Точка пересечения прямой с осью ординат имеет координаты (0, 4), и в уравнении (1) величина отрезка b = 4.
Таким образом, наше уравнение в отрезках на осях будет иметь вид
Уравнение прямой в отрезках: описание, примеры, решение задач
Продолжаем изучение раздела «Уравнение прямой на плоскости» и в этой статье разберем тему «Уравнение прямой в отрезках». Последовательно рассмотрим вид уравнения прямой в отрезках, построение прямой линии, которая задается этим уравнением, переход от общего уравнения прямой к уравнению прямой в отрезках. Все это будет сопровождаться примерами и разбором решения задач.
Уравнение прямой в отрезках – описание и примеры
Пусть на плоскости расположена прямоугольная система координат O x y .
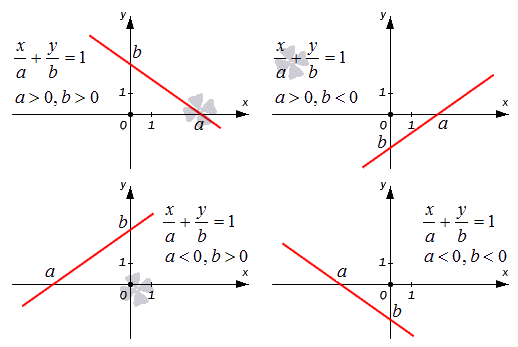
Прямая линия на плоскости в декартовой системе координат O x y задается уравнением вида x a + y b = 1 , где a и b – это некоторые действительные числа, отличные от нуля, величины которых равны длинам отрезков, отсекаемых прямой линией на осях O x и O y . Длины отрезков считаются от начала координат.
Как мы знаем, координаты любой из точек, принадлежащих прямой линии, заданной уравнением прямой, удовлетворяют уравнению этой прямой. Точки a , 0 и 0 , b принадлежат данной прямой линии, так как a a + 0 b = 1 ⇔ 1 ≡ 1 и 0 a + b b = 1 ⇔ 1 ≡ 1 . Точки a , 0 и b , 0 расположены на осях координат O x и O y и удалены от начала координат на a и b единиц. Направление, в котором нужно откладывать длину отрезка, определяется знаком, который стоит перед числами a и b . Знак « – » обозначает, что длину отрезка необходимо откладывать в отрицательном направлении координатной оси.
Поясним все вышесказанное, расположив прямые относительно фиксированной декартовой системы координат O x y на схематическом чертеже. Уравнение прямой в отрезках x a + y b = 1 применяется для построения прямой линии в декартовой системе координат O x y . Для этого нам необходимо отметить на осях точки a , 0 и b , 0 , а затем соединить эти точки линией при помощи линейки.
На чертеже показаны случаи, когда числа a и b имеют различные знаки, и, следовательно, длины отрезков откладываются в разных направлениях координатных осей.
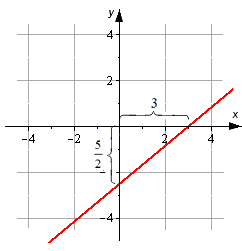
Прямая линия задана уравнением прямой в отрезках вида x 3 + y – 5 2 = 1 . Необходимо построить эту прямую на плоскости в декартовой системе координат O x y .
Решение
Используя уравнение прямой в отрезках, определим точки, через которые проходит прямая линия. Это 3 , 0 , 0 , – 5 2 . Отметим их и проведем линию.
Приведение общего уравнения прямой к уравнению прямой в отрезках
Переход от заданного уравнения прямой к уравнению прямой в отрезках облегчает нам решение различных задач. Имея полное общее уравнение прямой, мы можем получить уравнение прямой в отрезках.
Полное общее уравнение прямой линии на плоскости имеет вид A x + B y + C = 0 , где А , В и C не равны нулю. Мы переносим число C в правую часть равенства, делим обе части полученного равенства на – С . При этом, коэффициенты при x и y мы отправляем в знаменатели:
A x + B y + C = 0 ⇔ A x + B y = – C ⇔ ⇔ A – C x + B – C y = 1 ⇔ x – C A + y – C B = 1
Для осуществления последнего перехода мы воспользовались равенством p q = 1 q p , p ≠ 0 , q ≠ 0 .
В результате, мы осуществили переход от общего уравнения прямой A x + B y + C = 0 к уравнению прямой в отрезках x a + y b = 1 , где a = – C A , b = – C B .
Разберем следующий пример.
Осуществим переход к уравнению прямой в отрезках, имея общее уравнение прямой x – 7 y + 1 2 = 0 .
Решение
Переносим одну вторую в правую часть равенства x – 7 y + 1 2 = 0 ⇔ x – 7 y = – 1 2 .
Делим обе части равенства на – 1 2 : x – 7 y = – 1 2 ⇔ 1 – 1 2 x – 7 – 1 2 y = 1 .
Преобразуем полученное равенство к нужному виду: 1 – 1 2 x – 7 – 1 2 y = 1 ⇔ x – 1 2 + y 1 14 = 1 .
Мы получили уравнение прямой в отрезках.
Ответ: x – 1 2 + y 1 14 = 1
В тех случаях, когда прямая линия задана каноническим или параметрическим уравнением прямой на плоскости, то сначала мы переходим к общему уравнению прямой, а затем уже к уравнению прямой в отрезках.
Перейти от уравнения прямой в отрезках и общему уравнению прямой осуществляется просто: мы переносим единицу из правой части уравнения прямой в отрезках вида x a + y b = 1 в левую часть с противоположным знаком, выделяем коэффициенты перед неизвестными x и y .
x a + y b = 1 ⇔ x a + y b – 1 = 0 ⇔ 1 a · x + 1 b · y – 1 = 0
Получаем общее уравнение прямой, от которого можно перейти к любому другому виду уравнения прямой на плоскости. Процесс перехода мы подробно разобрали в теме «Приведение общего уравнения прямой к другим видам уравнения прямой».
Уравнение прямой в отрезках имеет вид x 2 3 + y – 12 = 1 . Необходимо написать общее уравнение прямой на плоскости.
Решение
Действует по заранее описанному алгоритму:
x 2 3 + y – 12 = 1 ⇔ 1 2 3 · x + 1 – 12 · y – 1 = 0 ⇔ ⇔ 3 2 · x – 1 12 · y – 1 = 0
Ответ: 3 2 · x – 1 12 · y – 1 = 0
Уравнение прямой в отрезках на осях
Уравнение прямой в отрезках на осях позволяет строить прямую в координатной плоскости без каких-либо дополнительных вычислений.
при условии a≠0, b≠0, c≠0 (то есть прямая не параллельна ни одной из осей координат и не проходит через начало отсчёта).
Перепишем уравнение в виде
и разделим обе части на -с:
Это — уравнение прямой в отрезках на осях, так как числа m и n соответствуют длинам отрезков (с соответствующими знаками), которые прямая отсекает на осях координат (считая от начала отсчёта).
В самом деле, в точке пересечения с осью Ox y=0:
В точке пересечения с осью Oy x=0:
отсекает на оси Ox отрезок -2, на оси Oy — отрезок 4.
Отмечаем на координатной плоскости точки (-2; 0) и (0;4) и проводим через них прямую.
Прямая
отсекает на оси Ox отрезок 3, на оси Oy — отрезок -6.
Отмечаем точки (3;0) и (0;-6) и проводим через них прямую.
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/uravnenie-prjamoj-v-otrezkah/
[/spoiler]