Как найти длину отрезка параболы - Сайт, где вы сможете решить свои вопросы

Приближение длины дуги эллипса с помощью ломаных

Длина кривой (или, что то же, длина дуги кривой) — числовая характеристика протяжённости этой кривой^[1]. Исторически вычисление длины кривой называлось спрямлением кривой (от лат. rectificatio, спрямление).

Определение[править | править код]

Для евклидова пространства длина отрезка кривой определяется как точная верхняя грань длин вписанных в кривую ломаных.

Например, пусть непрерывная кривая gamma в трёхмерном пространстве задана параметрически:

(1)

Приближение кривой ломаными

где , все три функции непрерывны и нет кратных точек, то есть разным значениям соответствуют разные точки кривой. Построим всевозможные разбиения параметрического интервала [a,b] на отрезков: ${displaystyle a=t_{0}<t_{1}<dots <t_{m}=b}$ . Соединение точек кривой ${displaystyle gamma (t_{0}),dots ,gamma (t_{m})}$ отрезками прямых даёт ломаную линию. Тогда длина отрезка кривой определяется как точная верхняя грань суммарных длин всех таких ломаных^[2].

Длина дуги циклоиды (s) в зависимости от её параметра (θ)

Связанные определения[править | править код]

Всякая кривая имеет длину, конечную или бесконечную. Если длина кривой конечна, то говорят, что кривая спрямляемая, в противном случае — неспрямляемая. Снежинка Коха — классический пример ограниченной, но неспрямляемой кривой; более того, любая, сколь угодно малая её дуга неспрямляема^[3].
Параметризация кривой длиной её дуги называется естественной.
Кривая есть частный случай функции из отрезка в пространство. Вариация функции, определяемая в математическом анализе, является обобщением длины кривой (см. ниже).

Свойства[править | править код]

Если все функции в (1) являются функциями ограниченной вариации, то длина кривой существует и конечна.

В математическом анализе выводится формула для вычисления длины отрезка кривой, заданной уравнениями (1), при условии, что все три функции непрерывно дифференцируемы:

$s=int limits _{a}^{b}{sqrt {{x'}^{2}(t)+{y'}^{2}(t)+{z'}^{2}(t)}},dt$

(2)

Формула подразумевает, что

и длина отсчитывается в сторону возрастания параметра t. Если рассматриваются два разных направления отсчёта длины от точки кривой, то часто удобно приписать дуге на одном из этих направлений знак минус.

В n-мерном случае вместо (2) имеем аналогичную формулу:

$s=int limits _{a}^{b}{sqrt {sum limits _{{k=1}}^{n}{f'_{k}}^{2}(t)}},dt$

${displaystyle s=int limits _{a}^{b}{sqrt {1+(f'(x))^{2}}},dx.}$

В полярных координатах

$s=int limits _{a}^{b}{sqrt {r^{2}+left({frac {dr}{dvarphi }}right)^{2}}},dvarphi .$

Формула Крофтона позволяет связать длину кривой на плоскости и интеграл числа её пересечений с прямыми по естественной мере на пространстве прямых.

История[править | править код]

Задача спрямления оказалась гораздо сложнее, чем вычисление площади, и в античные времена единственное успешное спрямление было выполнено для окружности. Декарт даже высказывал мнение, что «отношение между прямыми и кривыми неизвестно и, даже, думаю, не может быть познано людьми»^[4]^[5].

Первым достижением стало спрямление параболы Нейла (1657), выполненное Ферма и самим Нейлом. Вскоре была найдена длина арки циклоиды (Рен, Гюйгенс). Джеймс Грегори (ещё до открытия математического анализа) создал общую теорию нахождения длины дуги, которая немедленно была использована для различных кривых.

Вариации и обобщения[править | править код]

Риманово пространство[править | править код]

В n-мерном римановом пространстве с координатами $x^{1}cdots x^{n}$ кривая задаётся параметрическими уравнениями:

$x^{i}=x^{i}(t)qquad qquad$

((3))

Длина кривой в римановом пространстве задаётся формулой:

$s=int limits _{a}^{b}{sqrt {g_{{ij}}{dx^{i} over dt}{dx^{j} over dt}}},dt$

где : $g_{ij}$ — метрический тензор.
Пример: кривая на поверхности в $mathbb {R} ^{3}$ .

Общее метрическое пространство[править | править код]

В более общем случае произвольного метрического пространства (X,rho) длиной кривой называется вариация задающего кривую отображения, то есть длина кривой определяется согласно формуле:

$s=sup sum limits _{{k=0}}^{m}rho (gamma (x_{{k+1}}),gamma (x_{k})),$

где верхняя грань берётся, как и ранее, по всем разбиениям $a=x_{0}<x_{1}<dots <x_{m}=b$ отрезка [a,b] .

См. также[править | править код]

Дифференциальная геометрия кривых
Объём
Определённый интеграл
Площадь
Дуга окружности
Кривая Пеано

Примечания[править | править код]

↑ Длина // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 2.
↑ Шибинский, 2007, с. 199.
↑ Шибинский, 2007, с. 201—202.
↑ Ренэ Декарт. Геометрия. С приложением избранных работ П. Ферма и переписки Декарта / Перевод, примечания и статьи А. П. Юшкевича. — М.—Л.: Гостехиздат, 1938. — С. 49. — 297 с. — (Классики естествознания).
↑ Оригинал цитаты на французском языке: «la proportion qui est entre les droites et les courbes n’étant pas connue, et même, je crois, ne le pouvant être par les hommes», см. Descartes, René. Discours de la méthode…. — 1637. — С. 340.

Литература[править | править код]

Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973.
Мерзон Г. А., Ященко И. В. Длина, площадь, объем. — МЦНМО, 2011. — ISBN 9785940577409.
Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления в трёх томах. — Изд. 6-е. — М.: Наука, 1966.
Шибинский В. М. Примеры и контрпримеры в курсе математического анализа. Учебное пособие. — М.: Высшая школа, 2007. — 543 с. — ISBN 978-5-06-005774-4.

Источник

Парабола

Длина дуги параболы — это число, характеризующее протяжённость дуги параболы в единицах измерения длины.

Содержание

1 Обозначения
2 Формула
3 Вывод формулы
4 Другие формулы

Обозначения[править]

Введём обозначения:

x₁ — абсцисса первой точки дуги;

y₁ — ордината (меньшая) первой точки дуги;

x₂ — абсцисса второй точки дуги;

y₂ — ордината (большая) второй точки дуги;

y² = 2px — каноническое уравнение параболы;

L_{дуг.пар} — длина дуги параболы.

Формула[править]

${displaystyle L_{text{дуг.пар}}={frac {y_{2}{sqrt {y_{2}^{2}+p^{2}}}-y_{1}{sqrt {y_{1}^{2}+p^{2}}}}{2p}}+{frac {p}{2}}ln left|{frac {y_{2}+{sqrt {y_{2}^{2}+p^{2}}}}{y_{1}+{sqrt {y_{1}^{2}+p^{2}}}}}right|Leftrightarrow }$

${displaystyle Leftrightarrow L_{text{дуг.пар}}={frac {y_{2}{sqrt {2px_{2}+p^{2}}}-y_{1}{sqrt {2px_{1}+p^{2}}}}{2p}}+{frac {p}{2}}ln left|{frac {y_{2}+{sqrt {2px_{2}+p^{2}}}}{y_{1}+{sqrt {2px_{1}+p^{2}}}}}right|Leftrightarrow }$

${displaystyle Leftrightarrow L_{text{дуг.пар}}=signy_{2}{sqrt {x_{2}}}{sqrt {x_{2}+{frac {p}{2}}}}-signy_{1}{sqrt {x_{1}}}{sqrt {x_{1}+{frac {p}{2}}}}+{frac {p}{2}}ln left|{frac {signy_{2}{sqrt {x_{2}}}+{sqrt {x_{2}+{frac {p}{2}}}}}{signy_{1}{sqrt {x_{1}}}+{sqrt {x_{1}+{frac {p}{2}}}}}}right|}$

Заметим, что формула верна для точек с положительными и отрицательными ординатами, причём y₂ > y₁.

Вывод формулы[править]

${displaystyle L_{text{дуг.пар}}=int limits _{y_{1}}^{y_{2}}{sqrt {1+left[left({frac {y^{2}}{2p}}right)'right]^{2}}}dy=int limits _{y_{1}}^{y_{2}}{sqrt {1+left({frac {y}{p}}right)^{2}}}dy=int limits _{y_{1}}^{y_{2}}{sqrt {1+{frac {y^{2}}{p^{2}}}}}dy=}$

${displaystyle ={frac {1}{p}}int limits _{y_{1}}^{y_{2}}{sqrt {y^{2}+p^{2}}}dy=left.{frac {1}{2p}}left(y{sqrt {y^{2}+p^{2}}}+p^{2}ln left|y+{sqrt {y^{2}+p^{2}}}right|right)right|_{y_{1}}^{y_{2}}=}$

${displaystyle ={frac {1}{2p}}left(y_{2}{sqrt {y_{2}^{2}+p^{2}}}+p^{2}ln left|y_{2}+{sqrt {y_{2}^{2}+p^{2}}}right|-y_{1}{sqrt {y_{1}^{2}+p^{2}}}-p^{2}ln left|y_{1}+{sqrt {y_{1}^{2}+p^{2}}}right|right)}$

${displaystyle ={frac {y_{2}{sqrt {y_{2}^{2}+p^{2}}}-y_{1}{sqrt {y_{1}^{2}+p^{2}}}}{2p}}+{frac {p}{2}}ln left|{frac {y_{2}+{sqrt {y_{2}^{2}+p^{2}}}}{y_{1}+{sqrt {y_{1}^{2}+p^{2}}}}}right|Rightarrow }$

${displaystyle Rightarrow L_{text{дуг.пар}}={frac {y_{2}{sqrt {y_{2}^{2}+p^{2}}}-y_{1}{sqrt {y_{1}^{2}+p^{2}}}}{2p}}+{frac {p}{2}}ln left|{frac {y_{2}+{sqrt {y_{2}^{2}+p^{2}}}}{y_{1}+{sqrt {y_{1}^{2}+p^{2}}}}}right|}$

Для вывода используется формула длина дуги плоской кривой в прямоугольных координатах.
Для нахождения интеграла используется формула 1 интегралы функций с корнями.

Другие формулы[править]

длина дуги плоской кривой;
длина дуги окружности;
длина дуги параболы;
длина дуги эллипса;
длина дуги гиперболы;
длина дуги синусоиды;
длина дуги косинусоиды;
длина дуги циклоиды;
длина дуги кардиоиды;
длина дуги астроиды;
длина дуги эпициклоиды;
длина дуги гипоциклоиды;
длина дуги эвольвенты окружности;
длина дуги цепной линии;
длина дуги трактрисы;
длина дуги лемнискаты Бернулли.

Источник

2.1. Определение спрямляемой кривой и длины кривой

Пусть
на плоскости задана кривая
.
Разобьём эту кривую точкаминачастей и впишем в кривую ломаную,
соединяющую эти точки. Длинаэтой ломанной равна сумме длин
прямолинейных звеньев, соединяющих
точки разбиения:.
Устремим теперь количествоточек разбиения к бесконечности так,
чтобы максимальная длина звенастремилась к нулю. Если при этом
существует конечный предел последовательности
длин ломаных,
не зависящий от способа разбиения
кривой, то кривая называется спрямляемой,
а значение этого предела называется
длиной кривой.

2.2. Длина кривой в декартовых координатах

Пусть
теперь кривая
_–график
функции
,
имеющей непрерывную производную,.
Тогда длина кривой, заданной декартовым
уравнением,,
определяется формулой.

Типовой
пример

Найти
длину отрезка параболы
от точкидо точки.

►Здесь
,
поэтому

◄.

2.3.
Кривая задана параметрически
.
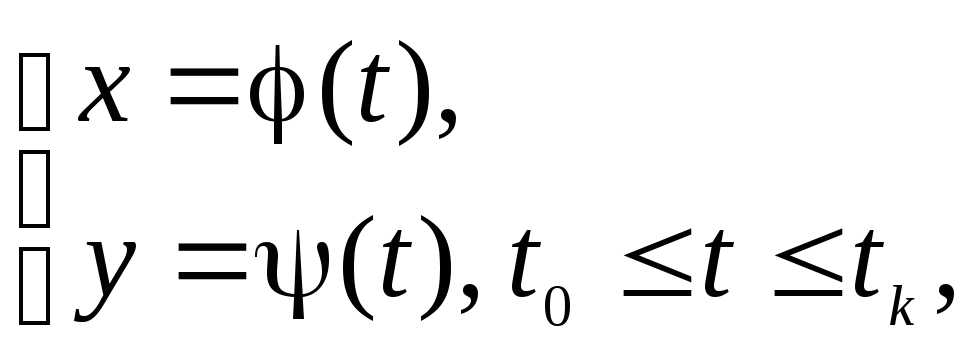
Заменим впеременнуюна переменную.
Так как,
то.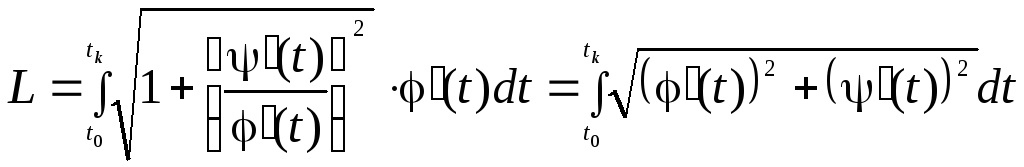
Итак, длина кривой, заданной параметрически,
определяется формулой.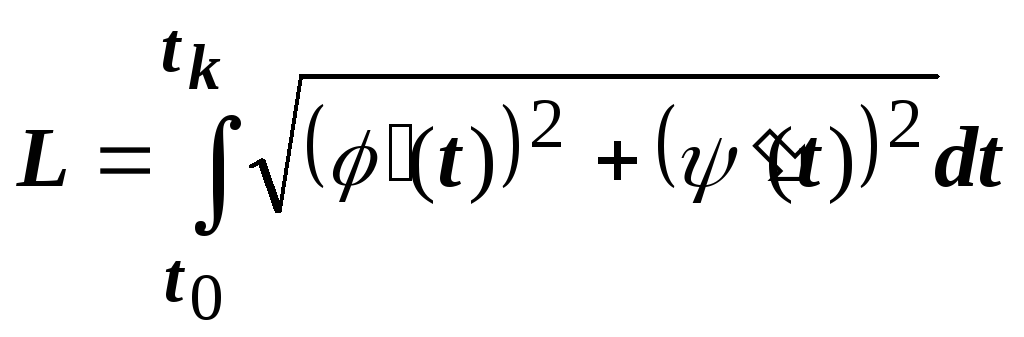

Типовой
пример

Вычислить
длину дуги кривой, заданной параметрическими
уравнениями
.

►Используем
формулу
.
Вычислим,.

Тогда
.◄

2.4. Кривая задана в полярных координатах

Случай,
когда кривая задаётся уравнением
,,
легко сводится к предыдущему. Так как,
то, рассматривая полярный уголкак параметр, получим,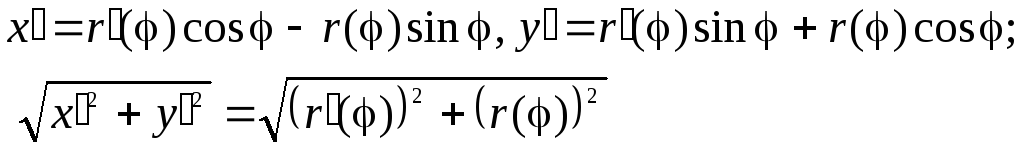

поэтому

Типовой
пример

Найти
длину кардиоиды
.

►Имеем
,
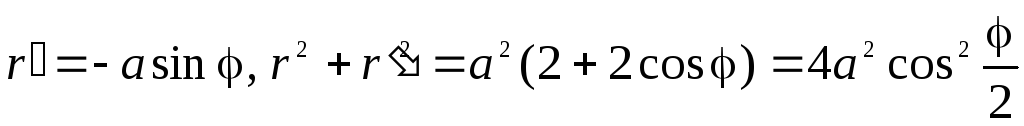поэтому.
Ответ явно бессмысленен. Где ошибка?
Ошибка в том, что упущен знак модуля при
извлечении корня из.
Правильное решение: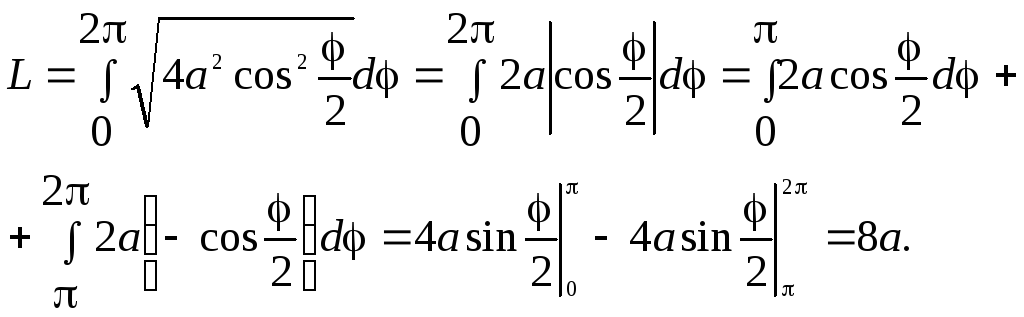

Однако,
как и в предыдущих случаях, проще
воспользоваться симметрией фигуры,
найти длину верхней ветви и удвоить её:
◄

3. Объёмы тел вращения

3.1.
Вычисление объёма тела по площадям
поперечных сечений
Пусть тело
расположено в пространстве между
плоскостямии,
и дляизвестна площадь его поперечного сечения.
Объём этого тела.

3.2. Объём тела, получающегося при вращении кривой вокруг координатной оси

Если
объём
получается в результате вращения кривой,,
вокруг оси,
то, очевидно,,
поэтому.

Типовой
пример

Вычислить
объем тела, полученного вращением кривых
ивокруг оси.

►Выполним
рисунок

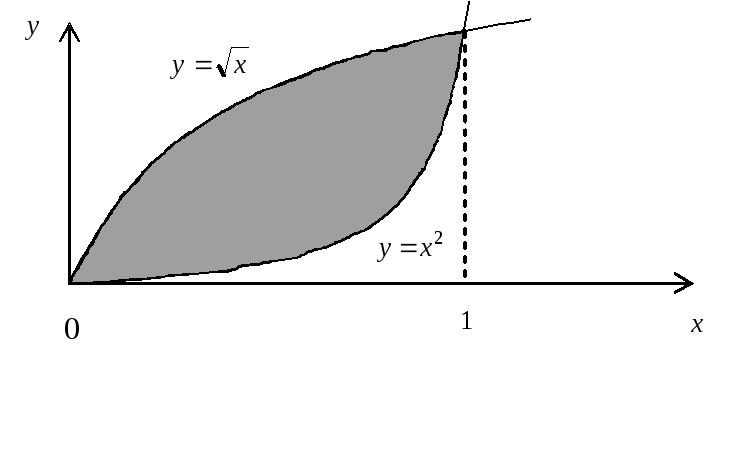
Находим
точку пересечения кривых:
;
;

.
Объем искомого тела получится вычитанием
из объема тела, полученного вращением
кривой
,
объема тела, полученного вращением
кривой:

ед.
куб. 
ед. куб. ◄

3.3.
Объём тела, получающийся при вращении
сектора, ограниченного кривой
и двумя полярными радиусамии,
вокруг полярной осинаходится
по формуле
.

Типовой
пример

Найти
объём тора, полученного вращением
окружности
вокруг полярной оси.

►

.◄

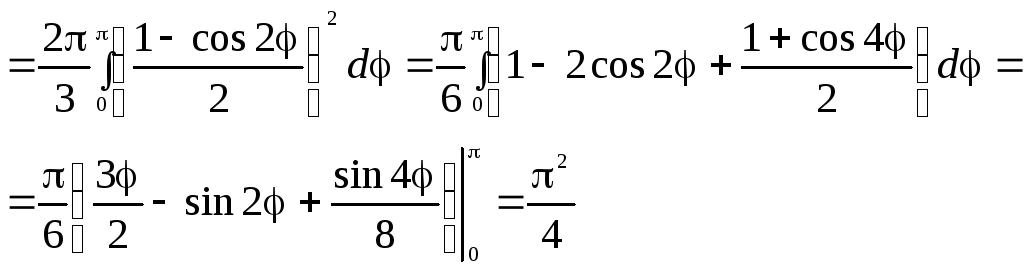4. Площадь поверхности вращения

Площадь
поверхности вращения, образующейся при
вращении вокруг оси
дифференцируемой кривой, определяется
по формулам (в зависимости от способа
задания кривой)

(–
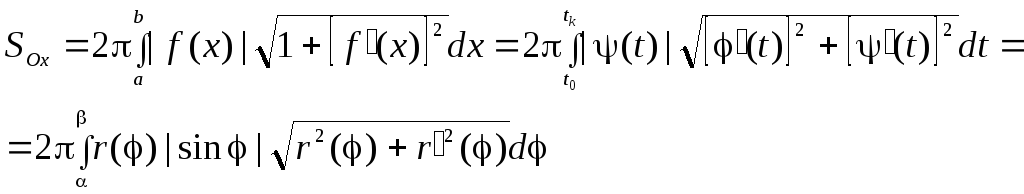
длина окружности кольца,–
его ширина).

Типовой
пример

Найти
площадь тора, образующегося при вращении
окружности
вокруг оси.

►Имеем
.◄

§4. Определенный интеграл в экономике

1. Экономический смысл определенного интеграла

Пусть
функция
описывает изменение производительности
некоторого производства с течением
времени. Найдем объем продукции,
произведенной за промежуток времени.
Если производительность не изменяется
с течением времени (– постоянная функция), то объем продукции,
произведенной за некоторый промежуток
времени,
задается формулой.
В общем случае справедливо равенство,
где,
которое оказывается тем более точным,
чем меньше.
Разобьем отрезокна промежутки времени точками:.
Для величины объема продукции,
произведенной за промежуток времени,
имеем,
где,,.

Тогда

При стремлении
к нулю каждое из использованных
приближенных равенств становится все
более точным, поэтому
.

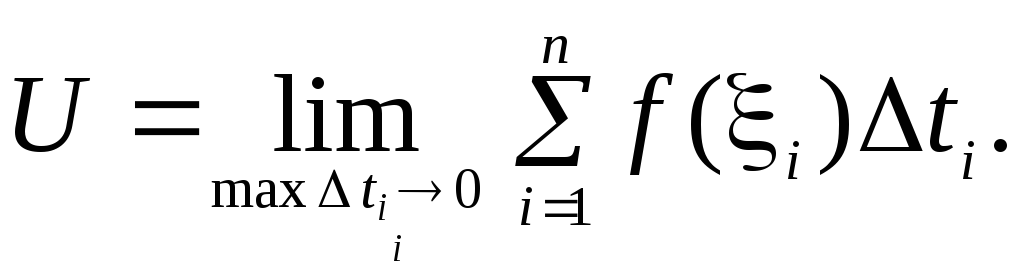Используя
определение определенного интеграла,
окончательно получаем:
,
т.е. если
– производительность труда в момент,
то

есть объем выпускаемой продукции за
промежуток
.

Величина
и объем продукции, произведенной за
промежуток
,
численно равны площади под графиком
функции,
описывающей изменение производительности
труда с течением времени, на промежутке.

Пример

Известно,
что численность населения определяется
формулой
,
где
–
число жителей в начальный момент
времени. Известно также, что потребление
населением в единицу времени некоторого
продукта пропорционально числу жителей.
Пусть коэффициент пропорциональности
равен
,
тогда функция потреблениябудет иметь вид:.
Найти объем продукта, необходимого для
потребления на промежуток времени.

►В
малый промежуток времени
количество жителей будем считать
постоянным, следовательно, за этот
элементарный промежуток времени
потребляется количество продукта.
Интегрируя это равенство, получим
количествопродукта, необходимое для населения на
весь промежуток времени отдо
.◄

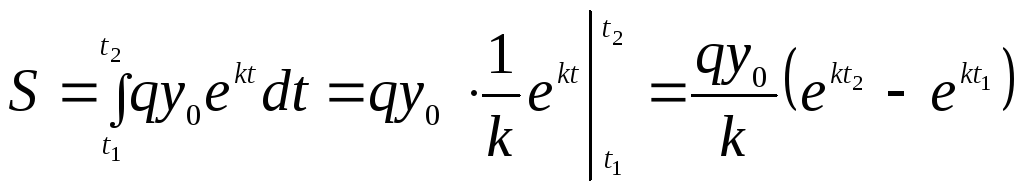Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Одним из приложений определенного интеграла является вычисление длины дуги плоской кривой. На рисунке изображен график функции
:

Для того, чтобы узнать длину дуги кривой линии изображенной на рисунке, необходимо
вычислить определенный интеграл:

В более общем случае, если у нас задана функция

в декартовых координатах и стоит задача найти длину дуги этой кривой между точками

и
,
нам необходимо вычислить интеграл:

В приведенной выше формуле, выражение

означает, что сначала нужно вычислить производную функции
,
а затем полученное выражение возвести в квадрат.

Наш онлайн калькулятор позволяет вычислить длину кривой, заданной в декартовых координатах для любой, даже очень сложной функции.

Источник

Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. “Практикум из математического анализа” (рядом стоит номер из сборника Б. П. Демидовича).

Для запоминания основных моментов схема интегрирования и вычисление дуги кривой из примера в пример будет повторяться. По возможности сами решения будут проиллюстрированы графиками кривых.

Найти длины дуг кривых в прямоугольной системе координат

Пример 2.117 (2431) Вычислить длину дуги кривой y=x^3/2 (полукубическая парабола Нейля) xє[0;4] .
Вычисление: Найдем производную заданной функции по переменной x:

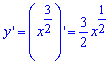
График полукубической параболы Нейля имеет вид

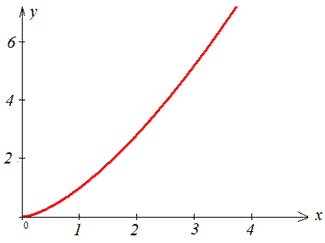
Выписываем пределы интегрирования:
a=0, b=4 (известны из начального условия).
По формуле находим длину дуги на заданном отрезке:

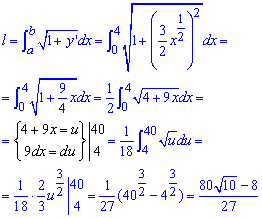
Во время интегрирования для приведения подынтегральной функции к табличному виду выполнили замену переменных.
При этом нужно перечислять пределы интегрирования.
В результате пришлось интегрировать корневую функцию, а длина дуги после вычислений приблизительно равна l=9,07.
Помните, что все длины измеряются в единицах (од.) !!!

Пример 2.118 (2432) Найти длину дуги кривой y²=2px (парабола) xє[0;x₀].
Вычисление: Поскольку отрезок дуги параболы задан в пределах [0;x₀], то заданная функция будет иметь вид положительной ветки корневой функции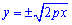
Вычислим производную функции по переменной x:

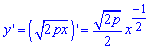
Запишем пределы интегрирования:
a=0, b=x₀ .

График параболы приведен ниже

Вычислим длину дуги через определенный интеграл:
для сведения к простым формулам интегрирования применяем замену переменных, при этом не забываем перечислить изменение пределов интегрирования:

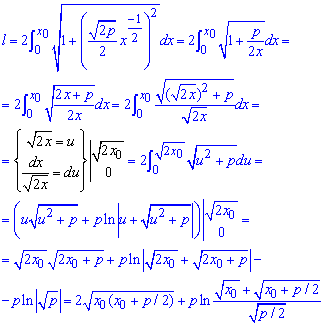
В конце вычислений применено интегрирование частями.

Пример 2.119 (2434) Найти длину дуги кривой y=e^x, [0;x₀].
Вычисление: Для интегрирования находим производную (по переменной x) экспоненты :
y’=(e^x)’=e^x.
Поскольку показатель не содержит никаких коэффициентов при переменной, то производная равна самой экспоненте.
Из начального условия выписываем пределы интегрирования:
a=0, b=x₀.
График экспоненты имеет вид

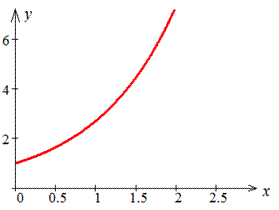
Чтобы вычислить длину дуги экспоненты переходим к новой переменной.
Это ведет к изменению и пределов интегрирования и самого дифференциала:

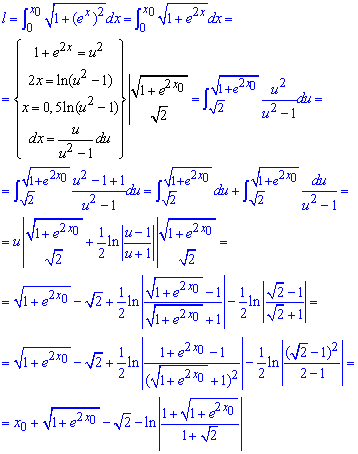
Напоследок расчетов приходим к формуле дуги, которая содержит корневую и логарифмическую зависимости от бегущей координаты.

Пример 2.120 ( 2435) Найти длину дуги кривой x=1/4y²-ln(y)/2, yє[1;e].
Вычисление: Вычислим производную (по переменной y ) заданной функции:

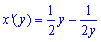
Приведенная формула работает и для обратных функций x=x(y), особенно если функция изменяется как показано на графике

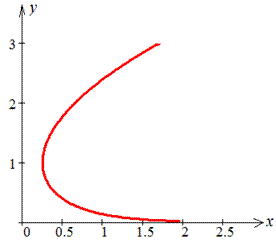
Пределы интегрирования: a=1, b=e .
Находим длину дуги кривой на заданном отрезке:

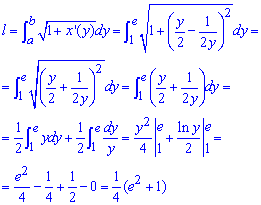
При возведении к квадрату производной получим простую для интегрирования функцию, которая в результате дает l=(e²+1)/4.

Пример 2.121 (2436) Вычислить длину дуги кривой

Вычисление: Найдем производную по переменной x функции:

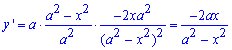
Пределы интегрирования для этой дуги равны [0;b].
График исследуемого логарифма имеет вид

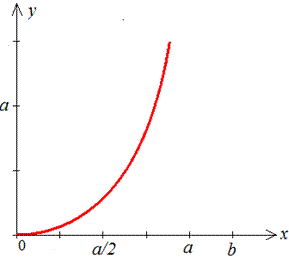
Интегрированием находим длину дуги кривой:

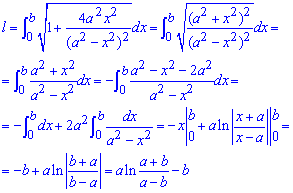
Со всеми превращениями подинтегральной функции попробуйте разобраться самостоятельно.

Пример 2.122 (2437) Вычислить длину дуги кривой y=ln(cos(x)), 0<x<a<Pi/2.
Вычисление: Найдем производную (по переменной x) заданной функции :

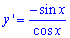
Запишем пределы интегрирования: 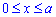(известны за условием).

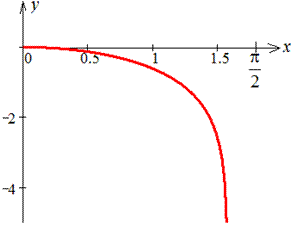
Вычислим длину дуги кривой на заданном отрезке:

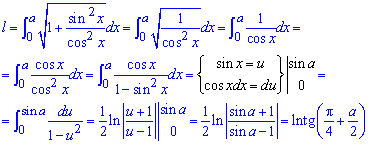
Если воспользоваться тригонометрическими формулами то перейдем к тангенсу, а сама длина дуги равна
l=ln(tg (Pi/4+a/2)).

Пример 2.123 Найти длину дуги кривой y=ln(x),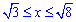
Вычисление: Вычисляем производную от логарифма:
y’=1/x.
Пределы интегрирования переписываем из условия: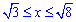

График логарифма имеет вид

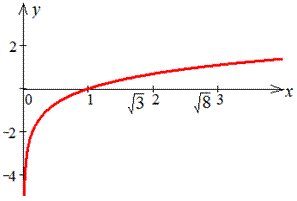
Интегрирование по длине дуги достаточно непростое, требует добрых умений.
Расписав подынтегральную функцию, и применив замену переменных к одному из интегралов, приходим к логарифмам, которые при указанных пределах интегрирования несколько упрощаются.

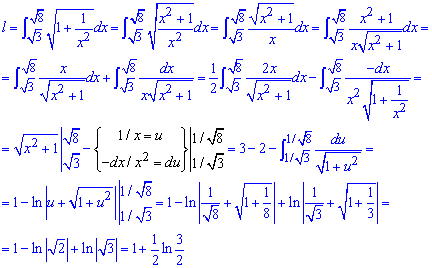
Невзирая на трехэтажные выражения конечное значение длины дуги выраженно простой зависимостью.

Пример 2.124 Найти длину дуги кривой y=ln(1-x₂), x[0;0,5].
Вычисление: Найдем производную (по переменной x) заданной функции :

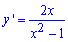
Из начального условия имеем такие пределы интегрирования: [0;0,5].
График исследуемого логарифма имеет вид

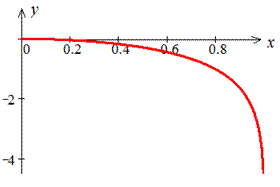
Вычисляем длину дуги логарифма:

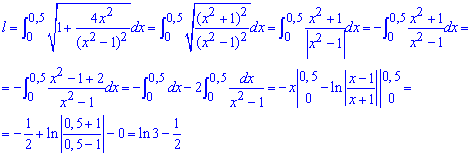
Если округлить конечное значение, то будем иметь l=0,5986.

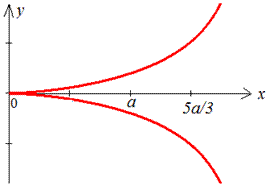
Пример 2.125 (2439) Вычислить длину дуги кривой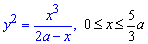
Вычисление: Поскольку график заданной функции симметричен относительно оси Ox, то вычислим длину дуги для положительной части функции

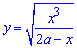
и результат умножим на 2.
Найдем производную функции и саму подинтегральную функцию:

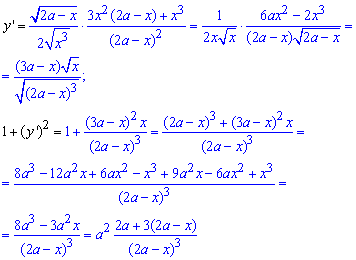
Пределы интегрирования известны: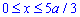

График веток в декартовой плоскости имеет вид.

При нахождении длины дуги дважды выполняем замену переменных.
Как и в предыдущих примерах ответ получаем через логарифмы

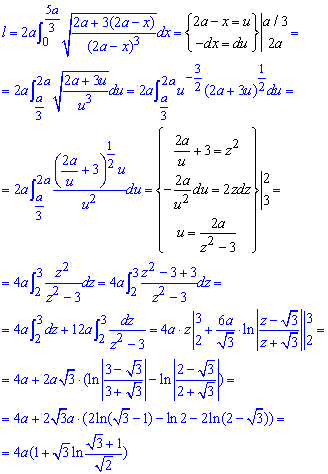
Кому в учебе придется вычислять подобное задание, просьба разобраться с превращениями.
А еще лучше – придумать и решить подобный пример.

Пример 2.126 (2438) Найти длину дуги кривой 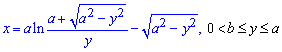(трактриса).
Вычисление: Запишем производную по переменной y трактрисы (см. 2408):

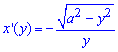
Пределы интегрирования:

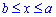
График трактрисы имеет вид

По формуле дуги кривой интегрируем и находим длину трактрисы:

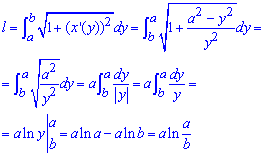
Конечная формула достаточно простая для расчетов.
От края следует несколько отойти, в ином случае длина трактрисы направляется к безконечности.

Пример 2433 Найти длину дуги кривой 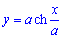(цепная линия) от точки A(0;a) к точке B(b;h) .
Вычисление: Цепная линия – это кривая, форму которой принимает цепь (нить) под действием силы притяжения, которая подвешена за оба конца.
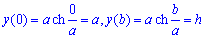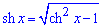Поскольку и , то

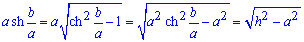
Найдем производную трактрисы:

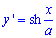
Пределы интегрирования по аргументу следующие:

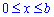
Рисунок цепной линии приведен ниже

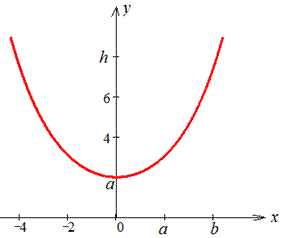
Вычислим длину дуги кривой на заданном отрезке:

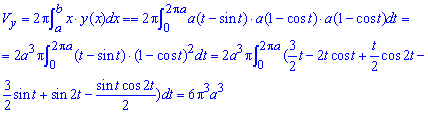
Пример 2440 Найти длину дуги астроиды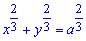
Вычисление: Для астроиды оси прямоугольной системы координат делят линию на 4 части (смотри 2429), поэтому длину будем искать для чверти и результат умножим на 4.
Выражаем функцию для чверти астроиды

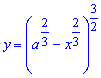
Найдем производную от полученной зависимости и подинтегральную функцию:

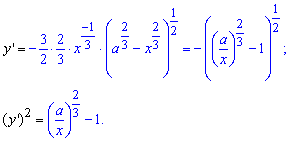
Пределы интегрирования: [0;a] (для чверти астроиды).
Вычислить длину дуги астроиды на практике достаточно легко:

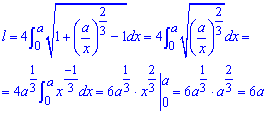
Дело в том, что единицы сокращаются и получаем простой табличный интеграл.
В результате длина астроиды равна l=6a.

Источник

Определение[править | править код]

Связанные определения[править | править код]

Свойства[править | править код]

История[править | править код]

Вариации и обобщения[править | править код]

Риманово пространство[править | править код]

Общее метрическое пространство[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Содержание

Обозначения[править]

Формула[править]

Вывод формулы[править]

Другие формулы[править]

2.1. Определение спрямляемой кривой и длины кривой

2.2. Длина кривой в декартовых координатах

2.4. Кривая задана в полярных координатах

3. Объёмы тел вращения

3.2. Объём тела, получающегося при вращении кривой вокруг координатной оси

4. Площадь поверхности вращения

§4. Определенный интеграл в экономике

1. Экономический смысл определенного интеграла

Найти длины дуг кривых в прямоугольной системе координат

Вам также может понравиться

Как исправить все ошибки в itunes

Пучок прямых как найти центр

Как найти степень окисления вещества hno3

Добавить комментарий Отменить ответ