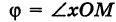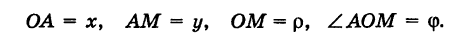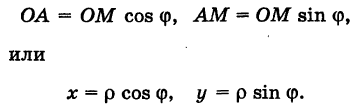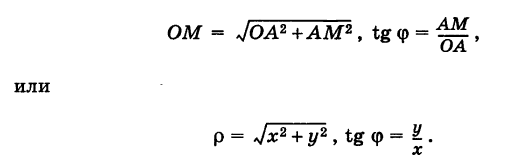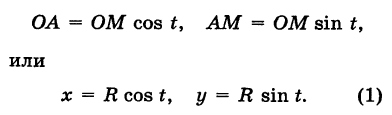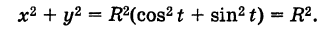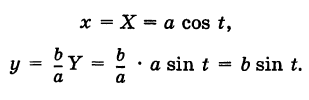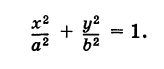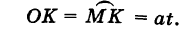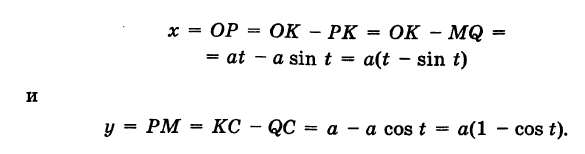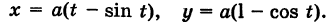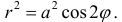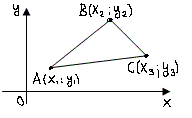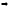How to find the distance between two points in polar Co-ordinates?
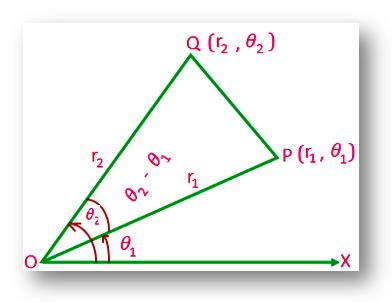
Let OX be the initial line through the pole O of the polar system and (r₁, θ ₁) and (r₂, θ₂) the polar co-ordinates of the points P and Q respectively. Then, OP₁ = r₁, OQ = r₂, ∠XOP = θ₁ and ∠XOQ = θ₂, Therefore, ∠POQ = θ₂ – θ₁.
From triangle POQ we get,
PQ² = OP² + OQ² – 2 ∙ OP ∙ OQ ∙ cos∠POQ
= r₁² + r₂² – 2r₁ r₂ cos(θ₂ – θ₁)
Therefore, PQ = √[r₁² + r₂ ² – 2r₁ r₂ cos(θ₂ – θ₁)].
Second Method: Let us choose origin and positive x-axis of the cartesian system as the pole and initial line respectively of the polar system. If (x₁, y₁) , (x₂, y₂) and (r₁, θ₁) (r₂, θ₂) be the respective Cartesian and polar co-ordinates of the points P and Q, then we shall have,
x₁ = y₁ cos θ₁, y₁ = r₁ sin θ₁
and
x₂ = r₂ cos θ₂, y₂ = r₂ sin θ₂.
Now, the distance between the points P and Q is
PQ = √[(x₂ – x₁)² + (y₂ – y₁)²]
= √[(r₂ cos θ₂ – r₁ cos θ₁)² + (r₂ sin θ₂ – r₂ sin θ₂)²]
= √[r₂² cos² θ₂ + r₁ ² cos² θ₁ – 2 r₁r₂ cos θ₁ cos θ₂ + r₂² sin² θ₂ + r₁²sin² θ₁ – 2 r₁r₁ sin θ₁ sin θ₂]
= √[r₂² + r₁² – 2r₁ r₂ Cos(θ₂ – θ₁)].
Example on distance between two points in polar Co-ordinates:
Find the length of the line-segment joining the points (4, 10°) and (2√3 ,40°).
Solution:
We know that the length of the line-segment joining the points (r₁, θ₁),and (r₂, θ₂), is
√[ r₂² + r₁² – 2r₁ r₂ Cos(θ₂ – θ₁)].
Therefore, the length of the line-segment joining the given points
= √{(4² + (2√3)² – 2 ∙ 4 ∙ 2√(3) Cos(40 ° – 10°)}
= √(16 + 12 – 16√3 ∙ √3/2)
= √(28 – 24)
= √4
= 2 units.
● Co-ordinate Geometry
- What is Co-ordinate Geometry?
- Rectangular Cartesian Co-ordinates
- Polar Co-ordinates
- Relation between Cartesian and Polar Co-Ordinates
- Distance between Two given Points
- Distance between Two Points in Polar Co-ordinates
- Division of Line Segment: Internal & External
- Area of the Triangle Formed by Three co-ordinate Points
- Condition of Collinearity of Three Points
- Medians of a Triangle are Concurrent
- Apollonius’ Theorem
- Quadrilateral form a Parallelogram
- Problems on Distance Between Two Points
- Area of a Triangle Given 3 Points
- Worksheet on Quadrants
- Worksheet on Rectangular – Polar Conversion
- Worksheet on Line-Segment Joining the Points
- Worksheet on Distance Between Two Points
- Worksheet on Distance Between the Polar Co-ordinates
- Worksheet on Finding Mid-Point
- Worksheet on Division of Line-Segment
- Worksheet on Centroid of a Triangle
- Worksheet on Area of Co-ordinate Triangle
- Worksheet on Collinear Triangle
- Worksheet on Area of Polygon
- Worksheet on Cartesian Triangle
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
Полярные координаты – определение и вычисление с примерами решения
Содержание:
Полярные координаты. параметрические уравнения линии
Полярные координаты
Основная идея метода координат состоит в том, что положение точки на плоскости однозначно определяется с помощью двух чисел. Конкретный геометрический смысл этих чисел дает ту или иную систему координат. Наиболее важной после прямоугольной системы, исключительно употреблявшейся нами до сих пор, является полярная система координат, к рассмотрению которой мы и переходим.
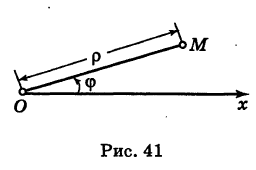
Возьмем на плоскости точку О, которую назовем полюсом. Проведем из полюса О направленную полупрямую Ох, называемую полярной осью (рис. 41).
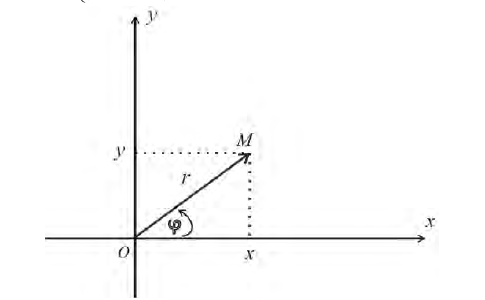
Пусть М — произвольная точка плоскости. Соединим точку М с полюсом О отрезком ОМ. Длина отрезка ОМ = р называется полярным радиусом точки М, а угол
Точка М с полярными координатами риф записывается следующим образом: М (р, ф), причем на первом месте ставится полярный радиус р, а на втором — полярный угол ф.
Что касается значений, принимаемых полярными координатами, то достаточно, очевидно, рассматривать значения р от 0 до 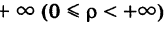
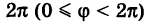
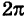
Связь между прямоугольными и полярными координатами
Рассмотрим переход от полярных координат к прямоугольным и обратно.
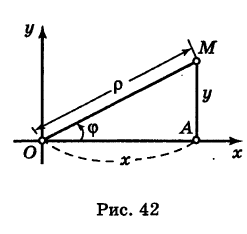
Предположим, что полюс полярной системы совпадает с началом прямоугольной системы координат Оху, а полярная ось является положительной полуосью Ох (рис. 42).
Тогда для произвольной точки М имеем
Считая угол ф острым, из прямоугольного треугольника АОМ находим
Полученные формулы справедливы для любого угла ф. Так выражаются прямоугольные координаты точки М через ее полярные координаты. Далее, из этого же прямоугольного треугольника АОМ получаем
Так выражаются полярные координаты точки через ее прямоугольные координаты.
Заметим, что при определении полярного угла ф по tg ф нужно учитывать знаки координат х и у.
Ранее мы видели, что линии могут быть заданы с помощью уравнений, связывающих их текущие прямоугольные координаты. Покажем теперь на простейшем примере, что линии могут определяться и уравнениями относительно полярных координат.
Пример:
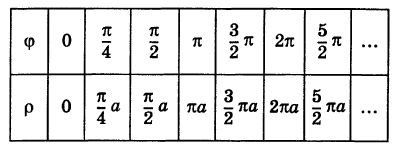
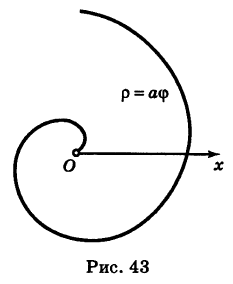
Рассмотрим кривую 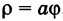
По этой таблице наносим точки и соединяем их линией, уточняя, если в этом есть необходимость, положение промежуточных точек (рис. 43).
Параметрические уравнения линии
Иногда бывает удобнее вместо уравнения линии, связывающего прямоугольные координаты 
Пример:
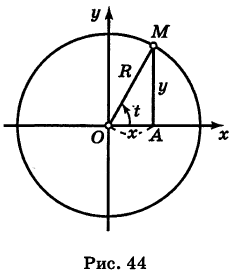
Выведем параметрические уравнения окружности.
Пусть М 
Это и есть параметрические уравнения окружности.
Чтобы получить обычное уравнение окружности, нужно исключить параметр t. Для этого возводим уравнения (1) в квадрат и складываем их:
Пример:
Выведем параметрические уравнения эллипса.
Эллипс с полуосями а и b можно рассматривать как равномерно сжатую вдоль вертикального диаметра окружность радиуса а, где коэффициент сжатия k = b/a. Пусть М (х, у) — точка эллипса, N (X, У) — соответствующая точка окружности (рис. 45), где
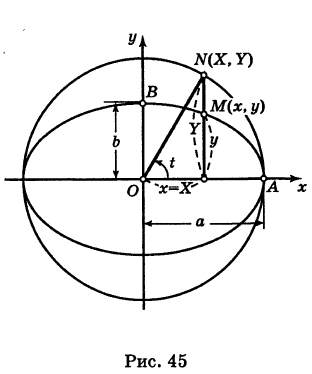
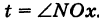
Таким образом, параметрические уравнения эллипса с полуосями а и b есть
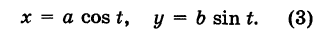
Имея параметрические уравнения линии, можно по точкам построить ее.
Пример:
Решение:
Составляем таблицу значений:
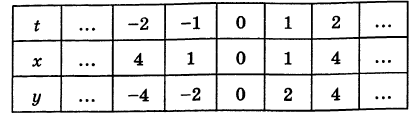
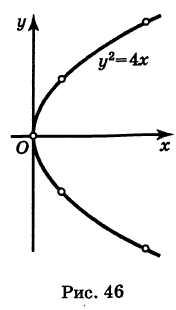
Эта кривая— парабола. В самом деле, исключив параметр t из уравнений (4), получим 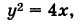
Параметрические уравнения циклоиды
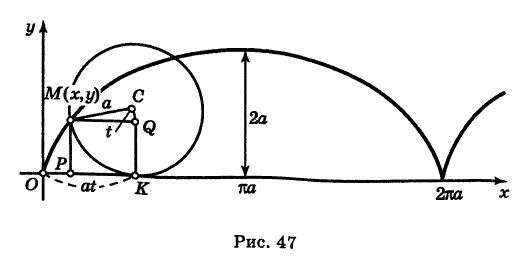
Определение: Циклоидой называется кривая, описываемая точкой окружности, катящейся без скольжения по прямой линии (рис. 47).
Выведем параметрические уравнения циклоиды, приняв прямую за ось Ох, предполагая, что радиус катящейся окружности равен айв начальном положении движущаяся точка М совпадает с началом координат. За параметр t примем угол поворота (в радианах) подвижного радиуса МС окружности относительно вертикального радиуса КС, где К — точка касания окружности с осью Ох (рис. 47). Так как качение окружности происходит без скольжения, то, очевидно, имеем
Отсюда на основании рис. 47 для координат текущей точки М циклоиды получаем следующие выражения:
Таким образом, параметрические уравнения циклоиды есть
Полярная система координат
Определение 1. Рассмотрим плоскость с прямоугольной декартовой системой координат Оху . Пусть М(х, у) – точка на плоскости, M ≠ 0. Полярными координатами точки М называются числа r − длина ее радиус-вектора (полярный
радиус) и ϕ − угол, образованный радиус-вектором с положительным направлением оси Ох (полярный угол), 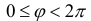
полюсом, а полуось Ох – полярной осью.
Замечание. Зависимость между прямоугольными (х, у) и полярными ( , ) r ϕ
координатами точки М задается в виде: 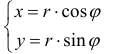
Рис.1. Полярные координаты точки.
Полярный полюс О и полярную ось можно выбрать на плоскости и не вводя
прямоугольную систему координат:
Пример 1.
Построим на плоскости линию, заданную уравнением:
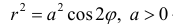
Решение.
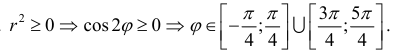
Вычислим значения r при различных значениях ϕ : 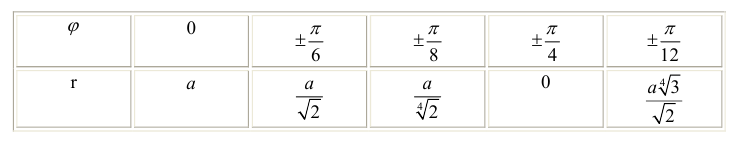
Проводим лучи из начала координат под углами ϕ к оси Ох и на них откладываем
отрезки длины r , получим :
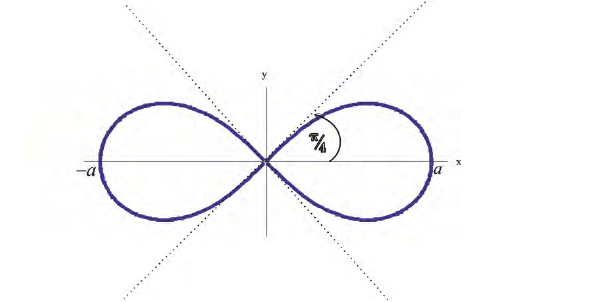
Рис.3. Лемниската
Пример 2.
а) Построим кривую 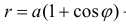
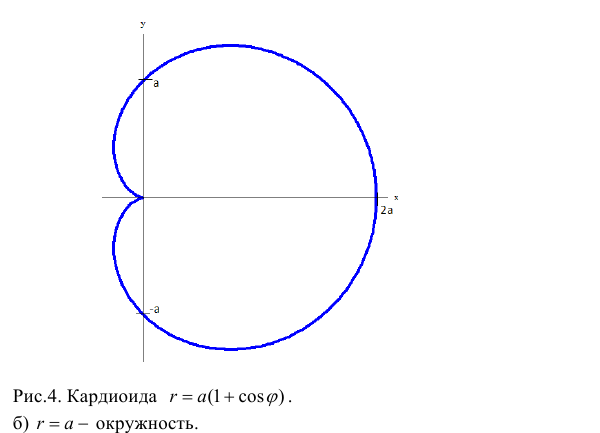
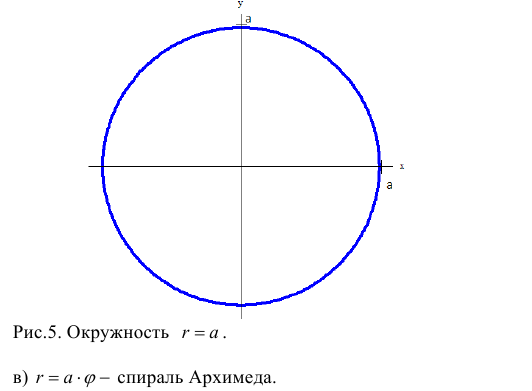
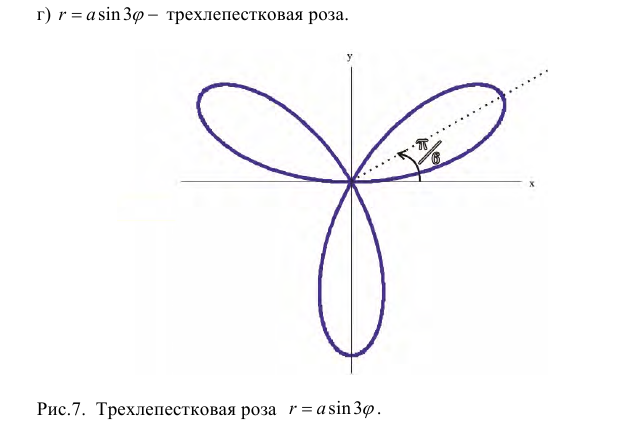
Замечание. Если в определении 1 отбросить требование 0 ≤ ϕ 0, то формулы (1) будут задавать непрерывное отображение точек плоскости (O, r, ϕ) на точки плоскости (x, O, y).
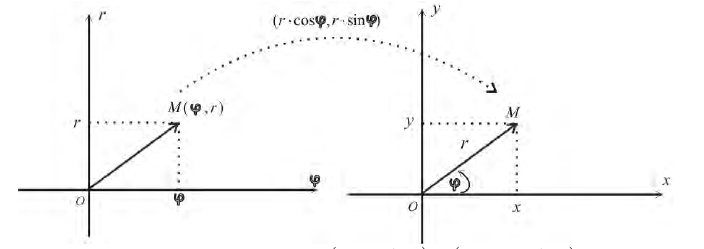
При этом, если r > 0, то векторы 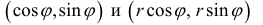
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Полярная система координат (полярные координаты)
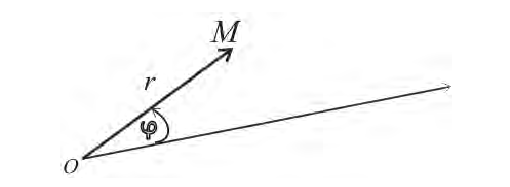
Полярная система координат на плоскости — это совокупность точки , называемой полюсом , и полупрямой , называемой полярной осью . Кроме того, задается масштабный отрезок для измерения расстояний от точек плоскости до полюса. Как правило, на полярной оси выбирается вектор , приложенный к точке , длина которого принимается за величину масштабного отрезка, а направление вектора задает положительное направление на полярной оси (рис.2.28,а).
Положение точки в полярной системе координат определяется расстоянием ( полярным радиусом ) от точки до полюса (т.е. ) и углом ( полярным углом ) между полярной осью и вектором . Полярный радиус и полярный угол составляют полярные координаты точки , что записывается в виде . Полярный угол измеряется в радианах и отсчитывается от полярной оси:
– в положительном направлении (против направления движения часовой стрелки), если значение угла положительное;
– в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.
Полярный радиус определен для любой точки плоскости и принимает неотрицательные значения . Полярный угол определен для любой точки плоскости, за исключением полюса , и принимает значения , называемыми главными значениями полярного угла . В некоторых случаях целесообразно считать, что полярный угол определен с точностью до слагаемых , где . В этом случае значениям полярного угла для всех соответствует одно и то же направление радиус-вектора.
С полярной системой координат можно связать прямоугольную систему координат , начало которой совпадает с полюсом, а ось абсцисс (точнее положительная полуось абсцисс) — с полярной осью. Ось ординат достраивается перпендикулярно оси абсцисс так, чтобы получилась правая прямоугольная система координат (рис.2.28,б). Длины базисных векторов определяются масштабным отрезком на полярной оси.
Наоборот, если на плоскости задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим полярную систему координат <связанную с данной прямоугольной).
Выведем формулы, связывающие между собой прямоугольные координаты точки , отличной от точки , и ее полярные координаты . По рис.2.28,б получаем
Эти формулы позволяют найти прямоугольные координаты по известным полярным координатам. Обратный переход выполняется по формулам:
Последние два равенства определяют полярный угол с точностью до слагаемых , где . При из них следует, что . Главное значение полярного угла находится по формулам (рис.2.29):
Пример 2.9. В полярной системе координат :
а) изобразить координатные линии ;
б) изобразить точки с полярными координатами . Найти главные значения полярных углов этих точек;
в) найти прямоугольные координаты точек .
Решение. а) Координатные линии представляют собой окружности соответствующих радиусов, а линии и — полупрямые (рис.2.30,а).
б) Построим точки и (рис.2.30,б,в). Их координаты отличаются полярным углом, однако, имеют одно и то же главное значение . Следовательно, это одна и та же точка, которая совпадает с точкой , изображенной на рис.2.30,а.
в) Учитывая пункт “б”, найдем прямоугольные координаты точки . По формулам (2.17) получаем:
1. Главное значение полярного угла можно выбрать иначе, например, .
2. Расстояние между двумя точками и (длина отрезка ) вычисляется по формуле
что следует из теоремы косинусов (рис.2.31).
3. Ориентированная площадь параллелограмма (рис.2.31), построенного на радиус-векторах и , находится по формуле
Она положительна, если (при этом ориентация пары радиус- векторов и правая), и отрицательна, если varphi_2″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAEcAAAASBAMAAAD73d5oAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMAwPxBoV0BgTEhELHR4JFxAbyQhgAAASJJREFUKM9jYCAdsEYRoyqmCqvwUgYGa1E4jy3mJczQCQzLRRZAOY8ZWBUPTUCoCvSEMGYzcJ0VcoCwOQUY1jZwFyAZbegBppwZ+Bw41CBC/AFALjuyIgZrCZCJxxgmMjBAFTFO4NrAwGLAwIlQNAWkiNkB6BCgNcYgZzE2sAYw9CSYX0cYJJwAVsQmwMAdsO7LDSCHbxt3A8dlhpniMIdDncSlwbGB7SHDbwZHEOdskalTAAMDTFEM1HMMnxyda6UYPjEUgThLlJRAeqGK4MHEwHpJ6T6I9gHzvNsY4IpYkQK8yQrkNg4NMEefAaEIGXwCqWFY2ADWrIxD0UGw+yVYQRS7Gg5FYBv4gq3B8QKONzvdSnRFBmA7lRQJJx22NKDLACxqN6Lf3w5xAAAAAElFTkSuQmCC” style=”vertical-align: middle;” /> (ориентация пары радиус-векторов и левая).
Пример 2.10. Даны полярные координаты и точек и (рис.2.32). Требуется найти:
а) скалярное произведение ;
б) длину отрезка ;
в) внешнее произведение ;
г) площадь треугольника ;
д) координаты середины отрезка в прямоугольной системе координат, связанной с данной полярной.
Решение. а) По определению скалярного произведения находим
б) Находим длину отрезка (см. пункт 2 замечаний 2.8):
в) Внешнее произведение находим как ориентированную площадь параллелограмма, построенного на векторах и :
Площадь положительная, так как векторы и образуют правую пару .
г) Площадь треугольника находим как половину площади параллелограмма, построенного на радиус-векторах и .
д) По формулам (2.17) находим прямоугольные координаты точек и :
а затем координаты середины отрезка (см. пункт 3 замечаний 2.1):
Пример 2.11. На координатной плоскости отмечена точка . Найти:
а) полярные координаты точки , образа точки при повороте радиус-вектора на угол вокруг начала координат (рис.2.33);
б) полярные координаты точки , образа точки при инверсии плоскости относительно окружности единичного радиуса с центром в начале координат (см. пример б преобразований плоскости в разд. 2.2.4).
Решение. а) Найдем полярные координаты точки . По формулам (2.17), учитывая рис.2.29, получаем:
так как точка лежит в четверти.
При повороте радиус-вектора вокруг полюса на угол полярный радиус не изменяется, а полярный угол увеличивается. Следовательно, полярные координаты точки : , , причем — главное значение полярного угла .
б) При инверсии относительно окружности радиуса полярные координаты образа выражаются через полярные координаты прообраза следующими формулами:
Поэтому, учитывая пункт “а”, находим (для ):
4.4. Уравнение линии в полярных координатах
По существу, уравнение линии в полярной системе координат представляет собой функцию полярного радиуса 





Полярную функцию можно сравнить со своеобразным радаром – когда луч света, исходящий из полюса, вращается против часовой стрелки и «прорисовывает» линию.
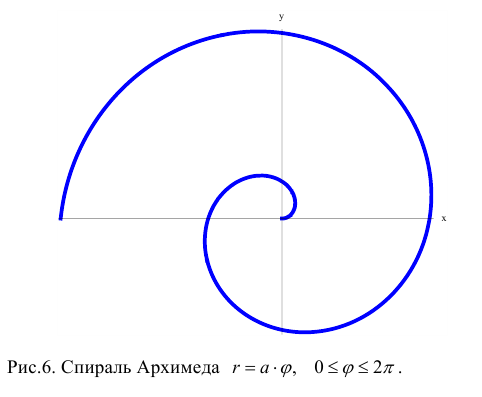
«Дежурным» примером полярной кривой является Архимедова спираль 


В первом же примере мы сталкиваемся и с понятием области определения полярной функции: поскольку полярный радиус неотрицателен , то отрицательные углы у функции рассматривать нельзя.
! Примечание: в ряде случаев принято использовать обобщённые полярные координаты, где радиус может быть отрицательным, и такой подход мы вкратце изучим чуть позже
Кроме спирали Архимеда, есть множество других известных кривых, но искусством, как говорится, сыт не будешь, поэтому я подобрал примеры, которые очень часто встречаются в реальных практических заданиях.
Сначала простейшие уравнения и простейшие линии:
Уравнение вида задаёт луч, исходящий из полюса. Действительно, вдумайтесь, если значение угла всегда (каким бы ни было «эр») постоянно, то какая это линия?
Примечание: в обобщённой полярной системе координат данное уравнение задаёт прямую, проходящую через полюс.
Уравнение вида определяет… догадайтесь с первого раза – если для любого угла «фи» радиус остаётся постоянным? Фактически это определение окружности с центром в полюсе радиуса .
Например, . Для наглядности найдём уравнение этой линии в прямоугольной системе координат. Используя полученную ранее формулу , проведём замену:
Возведём обе части в квадрат:
– уравнение окружности с центром в начале координат радиуса 2, что и требовалось проверить.
А теперь оценИте удобство – с окружностью значительно выгоднее работать именно в полярных координатах по причине предельной простоты уравнения .
Рассмотрим более содержательные задачи на построение:
Задача 116
Построить линию
Решение: в первую очередь найдём область определения. Так как полярный радиус неотрицателен, то должно выполняться неравенство . Можно вспомнить школьные правила решения тригонометрических неравенств, но в простых случаях как этот,
я советую более быстрый графический метод решения:
– Посмотрим на график функции (см. Приложение Тригонометрия). Что означает неравенство ? Оно означает, что нас устраивает тот кусок графика, который не ниже оси абсцисс , а именно, его часть на отрезке . И, соответственно, интервал не подходит. Таким образом, область определения нашей функции: , то есть график расположен справа от полюса (по терминологии декартовой системы – в правой полуплоскости).
В полярных координатах часто бывает смутное представление о том, какую линию определяет то или уравнение, поэтому чтобы её построить, необходимо найти принадлежащие ей точки – и чем больше, тем лучше. Обычно ограничиваются десятком-другим (а то и меньшим количеством). Проще всего, конечно же, взять табличные значения угла.
Для бОльшей ясности к отрицательным значениям угла я буду «прикручивать» один оборот (левая колонка), и в силу чётности косинуса соответствующие положительные значения можно заново не считать (справа):
Изобразим полярную систему координат и отложим найденные точки, при этом одинаковые значения «эр» удобно откладывать за один раз, делая парные засечки циркулем по рассмотренной ранее технологии:
В принципе, линия отчётливо прорисовывается, но чтобы стопроцентно подтвердить догадку, давайте найдём её уравнение в декартовой системе координат. Можно применить недавно выведенные формулы , но я расскажу вам о более хитром приёме.
Обе части уравнения искусственно домножаем на «эр»: и используем более компактные формулы перехода:
Выделяя полный квадрат, приводим уравнение к понятному виду:
– уравнение окружности с центром в точке , радиуса 2.
Коль скоро по условию требовалось просто выполнить построение и всё, плавно соединяем найденные точки линией. Ничего страшного, если получится немного неровно, вы же не обязаны были знать, что это окружность 😉
Почему мы не рассмотрели значения угла вне промежутка ?
Ответ прост: нет смысла. Ввиду периодичности функции нас ждёт бесконечный «бег» по построенной окружности.
Несложно провести нехитрый анализ и прийти к выводу, что уравнение вида задаёт окружность диаметра с центром в точке .
Образно говоря, все такие окружности «сидят» на полярной оси и обязательно проходят через полюс. Если же , то весёлая компания перекочует налево – на продолжение полярной оси (подумайте, почему).
Похожая задача для самостоятельного решения:
Задача 117
Построить линию и найти её уравнение в декартовой системе координат.
Систематизируем порядок решения задачи:
Находим область определения функции, для этого удобно посмотреть на синусоиду (Приложение Тригонометрия), чтобы сразу же понять, где синус неотрицателен.
На втором шаге рассчитываем полярные координаты точек, используя табличные значения углов; проанализируйте, нельзя ли сократить количество вычислений?
На третьем шаге откладываем точки в полярной системе координат и аккуратно соединяем их линией.
И, наконец, находим уравнение линии в декартовой системе координат.
Примерный образец решения в конце книги.
Общий алгоритм и технику построения в полярных координатах мы детализируем и существенно ускорим совсем скоро, но перед этим познакомимся ещё с одной распространённой линией:
[spoiler title=”источники:”]
http://mathhelpplanet.com/static.php?p=polyarnye-koordinaty
http://mathter.pro/angem/4_4_uravnenie_linii_v_polyarnyh_koordinatah.html
[/spoiler]
Полярная система координат (полярные координаты)
Полярная система координат на плоскости — это совокупность точки , называемой полюсом, и полупрямой
, называемой полярной осью. Кроме того, задается масштабный отрезок для измерения расстояний от точек плоскости до полюса. Как правило, на полярной оси выбирается вектор
, приложенный к точке
, длина которого принимается за величину масштабного отрезка, а направление вектора задает положительное направление на полярной оси (рис.2.28,а).
Положение точки в полярной системе координат определяется расстоянием
(полярным радиусом) от точки
до полюса (т.е.
) и углом
(полярным углом) между полярной осью и вектором
. Полярный радиус и полярный угол составляют полярные координаты точки
, что записывается в виде
. Полярный угол измеряется в радианах и отсчитывается от полярной оси:
– в положительном направлении (против направления движения часовой стрелки), если значение угла положительное;
– в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.
Полярный радиус определен для любой точки плоскости и принимает неотрицательные значения . Полярный угол
определен для любой точки плоскости, за исключением полюса
, и принимает значения
, называемыми главными значениями полярного угла. В некоторых случаях целесообразно считать, что полярный угол определен с точностью до слагаемых
, где
. В этом случае значениям
полярного угла для всех
соответствует одно и то же направление радиус-вектора.
С полярной системой координат можно связать прямоугольную систему координат
, начало
которой совпадает с полюсом, а ось абсцисс (точнее положительная полуось абсцисс) — с полярной осью. Ось ординат достраивается перпендикулярно оси абсцисс так, чтобы получилась правая прямоугольная система координат (рис.2.28,б). Длины базисных векторов определяются масштабным отрезком на полярной оси.
Наоборот, если на плоскости задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим полярную систему координат {связанную с данной прямоугольной).
Выведем формулы, связывающие между собой прямоугольные координаты точки
, отличной от точки
, и ее полярные координаты
. По рис.2.28,б получаем
(2.17)
Эти формулы позволяют найти прямоугольные координаты по известным полярным координатам. Обратный переход выполняется по формулам:
(2.18)
Последние два равенства определяют полярный угол с точностью до слагаемых , где
. При
из них следует, что
. Главное значение полярного угла
находится по формулам (рис.2.29):
Пример 2.9. В полярной системе координат :
а) изобразить координатные линии ;
б) изобразить точки с полярными координатами
. Найти главные значения полярных углов этих точек;
в) найти прямоугольные координаты точек .
Решение. а) Координатные линии представляют собой окружности соответствующих радиусов, а линии
и
— полупрямые (рис.2.30,а).
б) Построим точки и
(рис.2.30,б,в). Их координаты отличаются полярным углом, однако, имеют одно и то же главное значение
. Следовательно, это одна и та же точка, которая совпадает с точкой
, изображенной на рис.2.30,а.
в) Учитывая пункт “б”, найдем прямоугольные координаты точки . По формулам (2.17) получаем:
то есть
Замечания 2.8
1. Главное значение полярного угла можно выбрать иначе, например, .
2. Расстояние между двумя точками и
(длина отрезка
) вычисляется по формуле
что следует из теоремы косинусов (рис.2.31).
3. Ориентированная площадь параллелограмма (рис.2.31), построенного на радиус-векторах
и
, находится по формуле
Она положительна, если (при этом ориентация пары радиус- векторов
и
правая), и отрицательна, если
(ориентация пары радиус-векторов
и
левая).
Пример 2.10. Даны полярные координаты и
точек
и
(рис.2.32). Требуется найти:
а) скалярное произведение ;
б) длину отрезка ;
в) внешнее произведение ;
г) площадь треугольника
;
д) координаты середины отрезка
в прямоугольной системе координат, связанной с данной полярной.
Решение. а) По определению скалярного произведения находим
б) Находим длину отрезка (см. пункт 2 замечаний 2.8):
в) Внешнее произведение находим как ориентированную площадь параллелограмма, построенного на векторах и
:
Площадь положительная, так как векторы и
образуют правую пару
.
г) Площадь треугольника находим как половину площади параллелограмма, построенного на радиус-векторах
и
.
Так как (см. пункт “в”), то
.
д) По формулам (2.17) находим прямоугольные координаты точек и
:
а затем координаты середины отрезка
(см. пункт 3 замечаний 2.1):
Пример 2.11. На координатной плоскости отмечена точка
. Найти:
а) полярные координаты точки , образа точки
при повороте радиус-вектора
на угол
вокруг начала координат (рис.2.33);
б) полярные координаты точки , образа точки
при инверсии плоскости относительно окружности единичного радиуса с центром в начале координат (см. пример б преобразований плоскости в разд. 2.2.4).
Решение. а) Найдем полярные координаты точки . По формулам (2.17), учитывая рис.2.29, получаем:
так как точка лежит в
четверти.
При повороте радиус-вектора вокруг полюса на угол
полярный радиус не изменяется, а полярный угол увеличивается. Следовательно, полярные координаты точки
:
,
, причем
— главное значение полярного угла
.
б) При инверсии относительно окружности радиуса полярные координаты
образа выражаются через полярные координаты
прообраза следующими формулами:
Поэтому, учитывая пункт “а”, находим (для ):
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Простейшие задачи аналитической геометрии на плоскости
1. Расстояние между двумя точками.
Теорема
1.
Для любых двух точек




(1.1)
Например,
если
даны точки
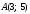
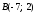
то расстояние между ними:

2. Площадь треугольника.
Теорема
2.
Для любых точек

не лежащих на одной прямой, площадь
треугольника


(1.2)
Например,
найдем площадь треугольника, образованного
точками




Замечание.
Если площадь треугольника равна нулю,
это означает, что точки лежат на одной
прямой.
3. Деление отрезка в заданном отношении.
Пусть
на плоскости дан произвольный отрезок
и
пусть

точка этого отрезка, отличная от точек
концов. Число

определенное равенством
называетсяотношением,
в
котором точка

.
Задача
о делении отрезка в данном отношении
состоит в том, чтобы по данному отношению
и данным координатам точек
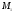


Теорема
3.
Если
точка
делит отрезок
в
отношении
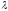
то
координаты этой точки определяются
формулами:





Следствие:
Если
– середина отрезка

где

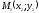
то

Например.
Даны точки
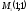

Найти координаты точки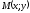
которая в два раза ближе к
чем к
Решение:
Искомая точка
делит
отрезок
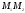
отношении

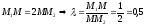
тогда
,
получили

Полярные координаты
Наиболее
важной после прямоугольной системы
координат является полярная система
координат. Она состоит из некоторой
точки
называемойполюсом,
и исходящего из нее луча

оси.
Кроме того, задается единица масштаба
для измерения длин отрезков.
Пусть
задана полярная система координат и
пусть

–
расстояние от точки
точки
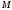

полярную ось для совмещения с лучом
Полярными
координатами точки

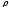

При этом число
радиусом,
число

углом.
Обозначается

Полярный радиус может иметь любое
неотрицательное значение:
Обычно считают, что полярный угол
изменяется в следующих пределах:
Однако в ряде случаев приходится
определять углы, отсчитываемые от
полярной оси по часовой стрелке.
Связь между полярными координатами точки и ее прямоугольными координатами.
Будем
считать, что начало прямоугольной
системы координат находится в полюсе,
а положительная полуось абсцисс совпадает
с полярной осью.
Пусть


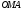

Тогда(1.5).
Эти формулы выражают прямоугольные
координаты через полярные.
С
другой стороны, по теореме Пифагора

(1.6)
– эти формулы, выражают полярные
координаты через прямоугольные.
Заметим,
что формула


так как
Из этих двух значений угла
равенства
Например,
найдем полярные координаты точки




т.к.
четверти
Пример
1:
Найти точку, симметричную точке
относительно
биссектрисы первого координатного
угла.
Решение:
Проведем
через точку А
прямую l1,
перпендикулярную биссектрисе l
первого координатного угла. Пусть

На прямой
l1
отложим отрезок
СА1,
равный
отрезку
АС.
Прямоугольные треугольники
АСО
и
А1СО
равны
между собой (по двум катетам). Отсюда
следует, что |ОА|
= |OA1|.
Треугольники
ADO
и
ОЕА1
также равны между собой (по гипотенузе
и острому углу). Заключаем, что
|AD|
= |ОЕ|
= 4,
|OD| = |EA1|
=
2, т.е. точка имеет координаты х
= 4, у = -2,
т.е. А1(4;-2).
Отметим,
что имеет место общее утверждение: точка
A1,
симметричная точке
относительно биссектрисы первого и
третьего координатных углов, имеет
координаты
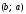
то есть
Пример
2:
Найти точку, в которой прямая, проходящая
через точки

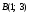
пересечет ось
Ох.
Решение:
Координаты
искомой точки
С
есть (x;
0). А так как точки
А,
В и
С
лежат на одной прямой, то должно
выполняться условие (x2-x1)(y3-y1)-(x3-x1)(y2-y1)=0
(формула (1.2), площадь треугольника ABC
равна
нулю!), где
–
координаты точки А,
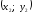
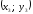
Получаем

т.е.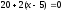


Следовательно, точка
С
имеет координаты


т.е.
Пример
3: В
полярной системе координат заданы точки


Найти:
а)
расстояние между точками
и

б)
площадь треугольника
ОМ1М2
(О
– полюс).
Решение:
а)
Воспользуемся формулами (1.1) и (1.5):

то
есть,
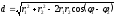
б)
пользуясь формулой для площади
треугольника со сторонами
а
и
b
и углом


находим площадь треугольника
ОМ1М2.

Наиболее важной после прямоугольной системы является полярная система координат.
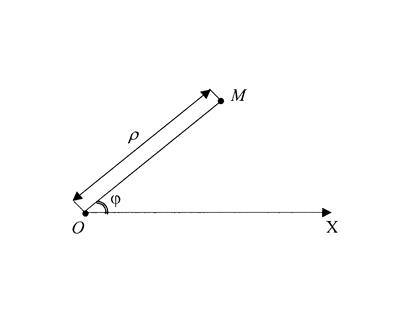
, которая называется полюсом. Проведем из полюса
направленную полупрямую
, называемую полярной осью (рис.18). Пусть
– произвольная точка плоскости. Соединим точку
С полюсом
Отрезком
. Длина отрезка
, т. е. расстояние точки
от полюса, называется
Полярным радиусом
точки , а угол
, отсчитываемый от полярной оси к отрезку
Против движения часовой стрелки,
Полярным углом
.
и полярный угол
и Составляют Полярные координаты точки
, и записывается следующим образом
.
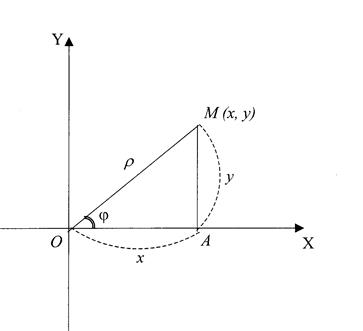
Рассмотрим переход от полярных координат к прямоугольным и обратно.
Пусть полюс полярной системы совпадает в началом прямоугольной системы координат , а полярная ось является положительной полуосью
(рис.19). Тогда для произвольной точки
имеем:
Считая угол острым, из прямоугольного
находим
Или
Полученные формулы справедливы для любого угла и выражают прямоугольные координаты точки
через ее полярные координаты.
Выразим полярные координаты точки через прямоугольные координаты из того же прямоугольника
Или
Пример 1. Найти полярное уравнение прямой
Решение. Так как , то
или
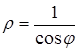
Пример 2. Написать уравнение линии в полярных координатах.
Решение. Так как , а
Подставим эти выражения в данное уравнение линии
или
Это уравнение данной линии в полярных координатах.
Иногда бывает удобнее вместо уравнения линии в прямоугольных координатах, рассматривать параметрические уравнения линии, дающие выражения текущих координат и
в виде функций от некоторой переменной величины
(параметра).
Пример 1. Выведем параметрическое уравнение окружности.
Решение. Пусть – произвольная точка окружности радиуса
с центром в начале координат (рис.20). В прямоугольном треугольнике
обозначим угол
через
. Будем иметь равенства
Или
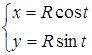
Это и есть параметрическое уравнение окружности.
Пример 2. Параметрическое уравнение эллиса.
Решение. Эллипс с полуосями и
можно рассматривать как равномерно сжатую вдоль вертикального диаметра окружность радиуса
, где коэффициент сжатия
. Пусть
– точка эллипса и
– соответствующая точка окружности (рис.21), где
. (1)
За параметр Примем угол, образованный радиусом
окружности с положительным направлением оси
:
Используя формулы (1) имеем
Таким образом, параметрические уравнения эллипса с полуосями и
есть
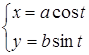
| < Предыдущая | Следующая > |
|---|