Числовой отрезок – это отрезок, по длине которого отложены равные отрезки, обозначенные цифрами.
Давайте взглянем на рисунок:
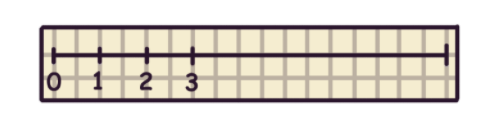 Характерной чертой числового отрезка является его конечность. Как видно на изображении, прямая ограничена с обеих сторон. Также мы замечаем числа – благодаря им отрезок и носит название числового. Каждый короткий отрезочек – расстояние от 0 до 1, от 1 до 2, от 2 до 3 – равен друг другу и называется единичным отрезком.
Характерной чертой числового отрезка является его конечность. Как видно на изображении, прямая ограничена с обеих сторон. Также мы замечаем числа – благодаря им отрезок и носит название числового. Каждый короткий отрезочек – расстояние от 0 до 1, от 1 до 2, от 2 до 3 – равен друг другу и называется единичным отрезком.
Но если Вы видите, что отрезок начинается нулём, а заканчивается стрелкой, знайте – это числовой луч.
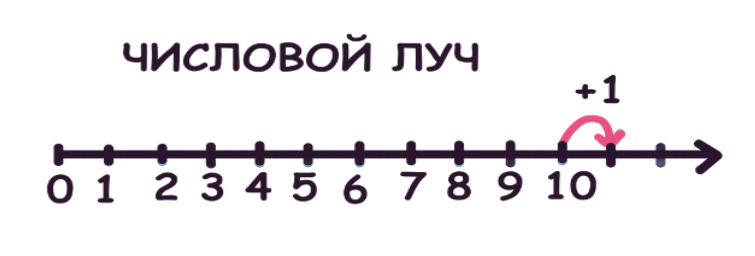 Числовой луч – это часть прямой линии, разъединённой на единичные отрезки.
Числовой луч – это часть прямой линии, разъединённой на единичные отрезки.
Особенностью числового луча является то, что он бесконечен.
А теперь давайте посмотрим, как умение работать с числовыми отрезками может помочь нам при счёте.
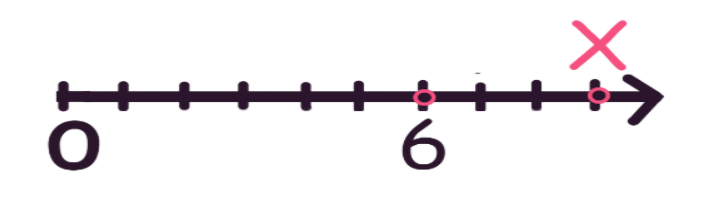
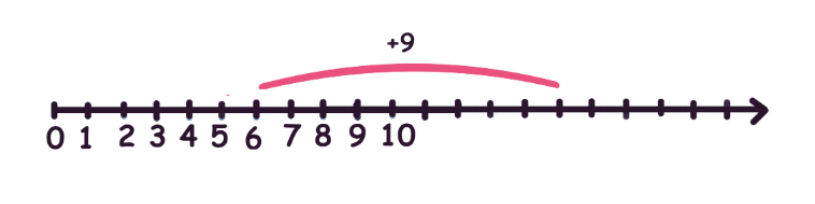 6 – точка, в которой мы изначально находимся. От этой точки предлагают сделать ещё 9 шагов. Наша задача – определить, какая длина числового отрезка получится после того, как мы переместимся на 9 единичных отрезков вправо.
6 – точка, в которой мы изначально находимся. От этой точки предлагают сделать ещё 9 шагов. Наша задача – определить, какая длина числового отрезка получится после того, как мы переместимся на 9 единичных отрезков вправо.
Рассуждаем:
Один единичный отрезок равен единице. Каждый единичный отрезок равен между собой. Длина известного числового отрезка составляет 6 единичных отрезков. Нам необходимо прибавить 9 единичных отрезков, чтобы узнать длину увеличенного числового отрезка.
На этом этапе можно поставить пальчик ребёнка на начало пути – точку 6 – и, двигаясь вправо, переходить с числа на число, считая каждый шаг и проговаривая, на каком числе Вы оказались:
Один шаг – 7, два шага – 8, три шага – 9 и так далее. До тех пор, пока Вы не сделаете все 9 шагов и не окажетесь в нужной нам точке – числе 15, которое станет известно благодаря пошаговому счёту. Так, длина интересующего нас числового отрезка составляет 15 единичных отрезков.
Вне числового луча этот пример имеет вид:
6 + 9 = 15
Помимо того, что числовые лучи и отрезки помогают при счёте, они приходятся очень кстати при сравнении чисел.
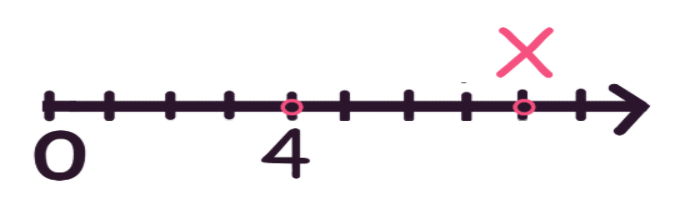 На числовом луче мы видим две отмеченные точки: 4 и Х. Х – неизвестное число. Узнать его не составляет труда: надо к 4 прибавить то количество единичных отрезков, которое расположено между 4 и Х:
На числовом луче мы видим две отмеченные точки: 4 и Х. Х – неизвестное число. Узнать его не составляет труда: надо к 4 прибавить то количество единичных отрезков, которое расположено между 4 и Х:
4 + 4 = 8
Очевидно, что число 8, которое пряталось за переменной Х, больше числа 4. Но если бы нас попросили дать быстрый ответ, значение какой из точек – 4 или Х – больше, мы бы смогли ответить без долгих раздумий. Потому что значение точки, которая на числовом луче или числовом отрезке стоит правее, всегда больше, чем значение точки слева.
Попробуйте определить, значение какой точки – 6 или Х – меньше?
Преподаватели онлайн-школы World of Math подготовили для Вашего чада задания, которые помогут систематизировать знания по теме “Числовой отрезок”. Много практики и толковое разъяснение материала ждут Вас на бесплатном уроке!
Записаться можно здесь
Ответ 1 группы. На заранее начерченной числовой прямой отмечают необходимые точки, цветным мелом выделяют изменения веса ребёнка. Дают ответ.
Учитель: Какую геометрическую фигуру вы выделили?
Учащиеся: Отрезок
Учитель: Как найти длину этого отрезка?
Учащиеся: Посчитать количество единичных отрезков или из большей координаты вычесть меньшую.

Ответ 2 группы. На заранее начерченной числовой прямой отмечают необходимые точки, цветным мелом выделяют изменения задолженности. Дают ответ.
Учитель: Какую геометрическую фигуру вы выделили?
Учащиеся: Отрезок
Учитель: Как найти длину этого отрезка?
Учащиеся: Посчитать количество единичных отрезков или из большей по модулю координаты вычесть меньшую.

Ответ 3 группы. На заранее начерченной числовой прямой отмечают необходимые точки, цветным мелом выделяют изменения веса ребёнка. Дают ответ.
Учитель: Какую геометрическую фигуру вы выделили?
Учащиеся: Отрезок
Учитель: Как найти длину этого отрезка?
Учащиеся: Посчитать количество единичных отрезков или сложить модули координат точек.

Учитель: Итак, какова тема нашего урока?
Учащиеся формулируют тему: Нахождение длины отрезка на координатной прямой.
Учитель: Запишите тему урока в тетрадь. Методы нахождения длины отрезка в каждой группе различны за исключением способа подсчёта количества единичных отрезков, что для больших чисел нерационально. Каковы цели урока.
Учащиеся:
-
Сформулировать правило нахождения длины отрезка на координатной прямой.
-
Научиться применять его при решении задач.
-
Привести примеры его использования в жизни.
Учитель: Продолжим работу в группах. По заданному рисунку составьте уравнение и решите его.

1 группа 2 группа 3 группа
3+х=9 -7+х= -2 -3+х=5
Решение всех уравнений записать в тетрадь.
Учитель: Чем является неизвестное в уравнении? Как его найти? Сформулируйте правило нахождения длины отрезка на координатной прямой. Если известно А(а) и В(b), чему равна длина отрезка АВ?
Может длина отрезка быть отрицательным числом? Подведём итог: Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца.

AC = 4 – ( – 2) = 4 + 2 = 6 .
Наше правило использует приёмы сложения и вычитания положительных и отрицательных чисел.
Учитель: Продолжим работу в группах. Приведите пример из жизни, который можно оформить и решить с помощью координатной прямой. Можно использовать такие предметы как география и история.
Учащиеся предлагают варианты.
Учитель: Оцените работу в группе каждого и на полях тетради карандашом поставьте оценку.
Фронтальная работа с классом.
1 ученик

2 ученик

Работа с учебником №1081 а, в, д – ученик у доски, класс работает одновременно с ним, б, г, е – самостоятельно на дополнительной доске другой ученик с последующей проверкой.
Самостоятельная работа на закрепление с самопроверкой по эталону.
Задание №1
Найдите длину отрезка АВ на координатной прямой, если:
-
A(-3,5); B(1.4)
-
А(-4,3); В(-5.4)
-
А(1,18); В(-5,2)
Задание №2
Начертите координатную прямую, отметите на ней точку А(-2) и отрезок АВ, длина которого 4 единичных отрезка. Запишите координату точки В.
5б – оценка 5
|
1 |
2 |
3 |
Задание 2 |
|
4,9 |
1,1 |
6,38 |
В(-6) и В(2) |
4б – оценка 4
3б – оценка 3
Менее3б – оценка 2
Домашнее задание №1095, 1096
Подведение итогов, повторение правила
Привет! Сегодня посмотрим задачи на отрезки из 15 задания ЕГЭ по информатике.
Решим с помощью шаблона на Python и помощью рассуждений. Повторите основные логические операции в этой статье.
Покажу Вам уникальный и понятный способ для борьбы с задачами на отрезки из 15 задания ЕГЭ по информатике.
Приступим к тренировочным задачам на отрезки.
Задача (Fight)
На числовой прямой даны два отрезка B=[10; 15] и С=[20; 27]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение
¬(((x ∈ B) ∨ (x ∈ C)) ⟶ (x ∈ A))
ложно (т.е. принимает значение 0) при любом значении переменной x.
Решение:
Решение с помощью шаблона на языке Python.
Приведу собственную разработку, как можно решить задачи на отрезки из 15 задания ЕГЭ по информатике с помощью шаблона на языке Python (Питон).
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 100): for b in range(a, 100): k=0 for i in range(1, 200): x = i/2 if not( (F(10, 15, x) or F(20, 27, x)) ) or F(a, b, x): k=k+1 if k==199: mn=min(mn, b-a) print(mn)
Здесь заводим функцию F(a, b, x). Она принимает три параметра: начало отрезка a, конец отрезка b и точку x. Если точка x лежит в отрезке [a;b], то функция вернёт True, иначе False.
Затем делаем два вложенных цикла. Это поиск отрезка A. Переменная a – это начало отрезка A. Переменная b – это конец отрезка A. Для каждой точки a пробуем различные точки b, которые находится правее, чем точка a. Мы начинаем проходить переменной b со значения a, потому что в некоторых задачах длина искомого отрезка A может быть равна нулю.
Для каждого отрезка-кандидата заводим счётчик k. Прокручиваем переменную i в диапазоне от 1 до 199 включительно. А x будет крутится от 0.5 до 99.5 с шагом 0.5, тем самым имитируя фразу при любых значениях x.
Внутри “цикла i” проверяем логическое выражение. Если выражение удовлетворяет условию задачи, то прибавляем к счётчику k единицу для данного отрезка A=[a; b].
При составлении логического выражения может помочь табличка.
| Логическая операция | Представление в Питоне |
| Отрицание ¬ | not() |
| Логическое умножение ∧ | and |
| Логическое сложение ∨ | or |
| Следование A ⟶ B | not(A) or B |
| Равносильность ≡ | == |
После окончания “цикла i” проверяем счёт k. Если логическое выражение сработало при всех значениях x, то в счётчике будет число 199. Это количество итераций в “цикле i”. Если такое выполняется, то нам подходит этот отрезок A.
Среди всех отрезков A, которые удовлетворяют условию задачи, выбираем с наименьшей длиной с помощью функции min.
Примечание: У нас всегда получается отрезок A c квадратными скобками на концах A=[a, b]. Даже, если в задачке должен быть отрезок с выколотыми точками, то на длину это никак не влияет, если мы ищем минимальный отрезок, поэтому всё равно будет получатся правильный ответ. Если же мы ищем наибольшую длину, нужно получать всегда отрезок A=(a,b) c выколотыми точками. Об этот речь пойдёт ниже.
Получается 17.
Решение с помощью рассуждений.
Видим, что ко всему выражению применяется логическое отрицание. Мы можем убрать это отрицание, но тогда нужно будет сделать, чтобы выражение было истинным, а не ложным.
В подобных задачах идём от обратного. Нам нужно найти, когда выражение будет истинным, но мы исследуем случай, когда выражение будет стремится ко лжи.

Найдём, при каких значениях x левое выражение будет выдавать 1.
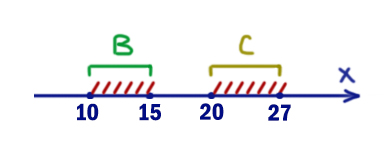
Здесь заштрихованы те иксы, которые приводят к тому, что левое выражение выдаёт 1. Это опасные x. Они “приближают” всё выражение к нулю.
Наша задача этого не допустить. У нас есть только один инструмент: подобрать такой отрезок A, чтобы правое выражение при опасных иксах выдавало 1. Тогда мы получим желаемый результат.
Т.е. при опасных иксах правое выражение должно выдавать 1. Чтобы покрыть все иксы приходится брать отрезок A=[10, 27].
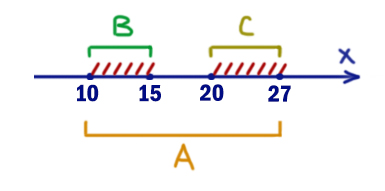
В ответе напишем длину отрезка A: 27 – 10 = 17. Здесь достаточно из наибольшей точки отнять наименьшую.
Ответ: 17
Задача (Раунд 2)
На числовой прямой даны два отрезка: B = [14; 20] и С = [15; 27]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение
¬(x ∈ A) ⟶ ((x ∈ B) ≡ (x ∈ C))
истинно (т.е. принимает значение 1) при любом значении переменной x.
Решение:
Решение с помощью шаблона на языке Python.
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 100): for b in range(a, 100): k=0 for i in range(1, 200): x=i/2 if F(a, b, x) or (F(14, 20, x) == F(15, 27, x)): k=k+1 if k==199: mn=min(mn, b-a) print(mn)
Получается ответ 13.
Решение с помощью рассуждений.
“Главной скрипкой” логического выражение является следование. Именно эта операция соединяет большие блоки логического выражения.
Нас будет интересовать тот случай, когда логическое выражение, наоборот, будет стремится к 0. Тогда правое логическое подвыражение должно равняться 0, а с помощью левого подвыражения, где находится отрезок A, мы будем исправлять ситуацию.

Заштрихуем те значения x, при которых правое подвыражение даёт ноль. Равносильность даёт ноль, когда два выражения имеют разные значения. Т.е. если x находится в одном отрезке, то в другом отрезке его не должно быть.
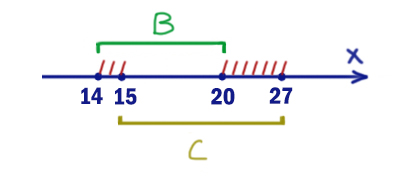
В подобных задачах можно не обращать внимание на закрашенные и выколотые точки на концах отрезков, потому что в дальнейшем нужно найти длину отрезка A, а длина от этого не зависит. Поэтому пишем и рисуем отрезки с некоторым приближением до одной точки.
Получаются два отрезка [14; 15) и (20; 27]. Это и есть “опасные” значения x. При этих значениях выражение уже “наполовину” ложно. Но с помощью A мы не дадим превратится ему в 0 при любых иксах.
Если левое подвыражение будет равно 1 при опасных значениях икс, то как раз получится то, что нам не нужно. Поэтому при опасных значениях иск, в левом выражении должен быть ноль.
Т.к. там стоит отрицание, убрав его, можно сказать, что в левом подвыражении должна стоять 1 при опасных значениях икс.
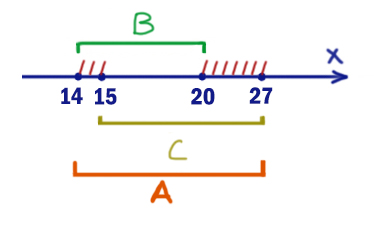
Чтобы покрыть все два отрезка опасных значений, выбираем A=[14; 27]. Нас просили найти минимальный отрезок A. Меньше не можем взять, т.к. тогда не все заштрихованные иксы будут закрыты.
Длина получается 27 – 14 = 13.
Ответ: 13
Задача (Отрезок максимальной длины)
На числовой прямой даны два отрезка: P = [43; 49] и Q = [44; 53]. Укажите наибольшую возможную длину такого отрезка A, что формула
((x ∈ A) → (x ∈ P)) ∨ (x ∈ Q)
тождественно истинна, то есть принимает значение 1 при любых x.
Решение:
Решение с помощью шаблона на языке Python.
def F(a, b, x): if a <= x <= b: return True else: return False def F2(a, b, x): if a < x < b: return True else: return False mx=0 for a in range(0, 100): for b in range(a, 100): k=0 for i in range(1, 200): x=i/2 if (not(F2(a, b, x)) or F(43, 49, x)) or F(44, 53, x): k=k+1 if k==199: mx=max(mx, b-a) print(mx)
Ответ получается 10. Здесь ищем максимальный отрезок A. При поиске отрезка максимальной длины, нужно создать функцию F2, и её применять к отрезку A, чтобы получался всегда отрезок с выколотыми точками A=(a, b).
Решение с помощью рассуждений.
Главная скрипка – это логическое или. Эта логическая операция соединяет два больших выражения.
Идём от обратного. Исследуем, когда выражение будет стремится к 0.

Логическое или выдаёт ноль, когда оба выражения равны нулю.
В начале лучше разобраться с тем выражением, где нет отрезка A. Это правое подвыражение. Там должен получаться ноль. Заштрихуем те иксы, которые выдают в правом подвыражении ноль.
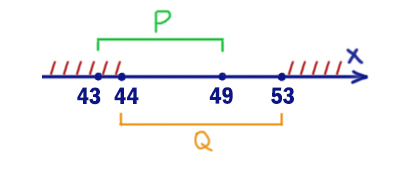
В левом выражение стоит следование. Эта операция равна нулю, когда из 1 следует 0. С помощью отрезка A мы будем спасать ситуацию. Заштрихуем, когда икс НЕ принадлежит P. Добавим это действие к предыдущей штриховке.
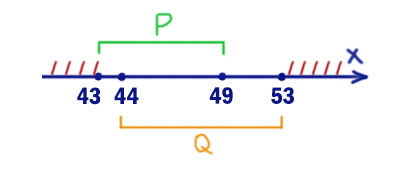
Таким образом, мы получили опасные иксы. Это все иксы, кроме отрезка [43; 53].
Именно при этих иксах выражение (x ∈ A) не должно выдавать 1. Выбираем отрезок A=[43; 53].
Мы могли бы взять отрезок и меньше, например [44; 49], но нас просили взять наибольший отрезок.
Длина равна 53 – 43 = 10.
Ответ: 10
Задача (Крепкий орешек)
На числовой прямой даны три интервала: P=[10,15], Q=[5,20] и R=(15,25]. Определите наименьшую возможную длину отрезка A, при выборе которого выражение
((x ∉ A) → (x ∈ P)) ≡ ((x ∈ Q) → (x ∈ R))
будет ложно при любых x.
Решение:
Решение с помощью шаблона на языке Python.
def F(a, b, x): if a <= x <= b: return True else: return False def F2(a, b, x): if a < x <= b: return True else: return False mn=10**9 for a in range(0, 100): for b in range(a, 100): k=0 for i in range(1, 200): x = i / 2 if not( (F(a, b, x) or F(10, 15, x)) == (not(F(5, 20, x)) or F2(15, 25, x)) ): k=k+1 if k==199: mn=min(mn, b-a) print(mn)
Здесь заводим ещё одну функцию F2 для отрезка R с выколотой левой точкой. Ответ получается 5.
Решение с помощью рассуждений.
Нужна ложь, но мы рассмотрим, когда равносильность выдаёт 1.
1) Рассмотрим первый случай 1 ≡ 1.
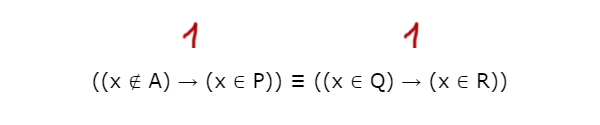
Рассмотрим левое выражение. Узнаём, когда оно выдаёт ноль, а потом сделаем инверсию, чтобы не рассматривать 3 случая.
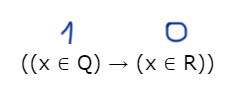
Получается, что в отрезке Q иксы должны находится, а в R нет.
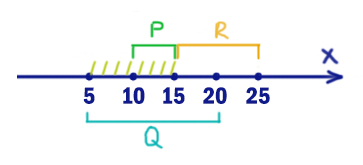
Сделаем инверсию.
Получается интервал x ∈ (-∞ 5) U (15; ∞). Это те иксы, при которых в правом выражении будет 1.
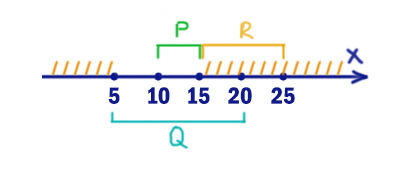
Рассмотрим, когда левое выражение выдаёт 1.
a) 0 → 0
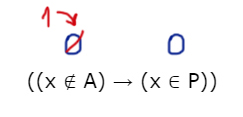
Учитывая вышеописанный интервал, понимаем, что иксы и так не лежат в отрезке P. Чтобы спаси ситуацию, нужно, чтобы выражение (x ∉ A) выдавало 1, при x ∈ (-∞ 5) U (15; ∞). Тогда левое выражение будет выдавать 0, а правое 1.
Следовательно, можем выбрать любой отрезок A в интервале [5; 15].
б) 0 → 1
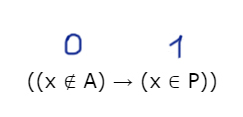
При x ∈ (-∞ 5) U (15; ∞) выражение (x ∈ P) никогда не выдаст 1. Значит, в этом варианте 1 ≡ 1 никогда не будет.
в) 1 → 1
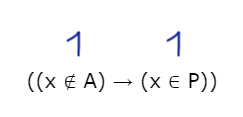
Аналогично невозможна и эта ситуация.
Перейдём ко второму случаю.
2) Рассмотрим случай 0 ≡ 0.
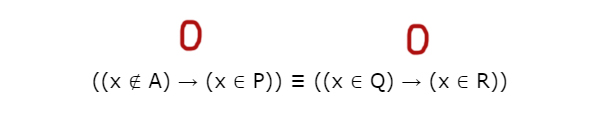
Когда правое выражение выдаёт ноль, мы уже смотрели. Это отрезок [5; 15].
Изучим те значения x, при которых левое выражение тоже будет выдавать 0 на отрезке [5; 15].
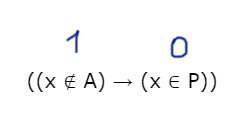
Тогда опасные иксы будут выглядеть следующим образом:
Т.е. это интервал [5; 15], но без отрезка P. Именно при x ∈ [5; 10) мы должны получать 0 в выражении (x ∉ A), чтобы спасти ситуацию. Получается A=[5;10). Меньше взять отрезок не можем, иначе не все опасные иксы будут покрыты.
Этот отрезок хорошо соотносится с первым вариантом 1) 1 ≡ 1.
Ответ получается 10 – 5 = 5.
Ответ: 5
Задача (Вперёд к победе!)
На числовой прямой даны два отрезка: D = [17; 58] и C = [29; 80]. Укажите
наименьшую возможную длину такого отрезка A, для которого логическое
выражение.
(x ∈ D) → ((¬(x ∈ C) ∧ ¬(x ∈ A)) → ¬(x ∈ D))
истинно (т.е. принимает значение 1) при любом значении переменной х.
Решение:
Решение с помощью шаблона на языке Python.
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 100): for b in range(a, 100): k=0 for i in range(1, 200): x = i / 2 if not(F(17, 58, x)) or (not((not(F(29, 80, x)) and not(F(a, b, x)))) or not(F(17, 58, x))): k=k+1 if k==199: mn=min(mn, b-a) print(mn)
Решение с помощью рассуждений.
“Главной скрипкой” данного логического выражения является следование, потому что эта операция соединяет различные логические блоки.
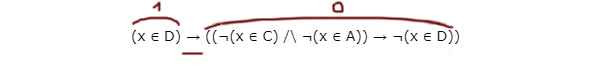
Нам нельзя допустить, чтобы первое выражение принимало 1, а второе 0, одновременно.
Рассмотрим при каких значениях x реализуется этот страшный вариант.
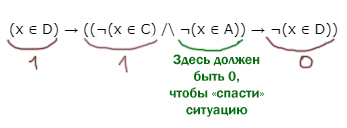
Видно, что, если левое выражение (x ∈ D) равно 1, то ¬(x ∈ D) в правой части автоматически выдаёт 0.
Чтобы умножение в правой части давало 1, необходимо, чтобы выражение ¬(x ∈ C) было истинным.
Тогда опасные значения – это отрезок D без отрезка C. Т.е., чтобы иксы были в отрезке D, но не были в отрезке С одновременно.
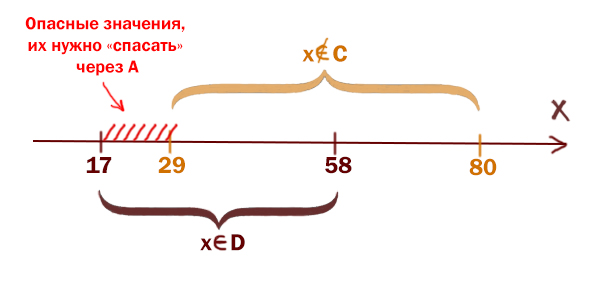
Опасные значения получаются [17; 29]. Чтобы опасный сценарий нейтрализовать, выражение ¬(x ∈ A) должно принимать значение 0. Тогда (x ∈ A) должно выдавать 1. Чтобы это происходило всегда при опасных значениях, принимаем A=[17, 29]. Длина получается 12.
Ответ: 12
Александр, а вот зачем в первой задаче учитывать вещественные x(я про деление i на 2), ведь если брать x целыми, то ответ не меняется. Это может быть критично в других задачах? И в каких случаях это повлияет на ответ?
Да, ответ может совпадать, но, например, в задаче “Крепкий орешек”, из этой статьи, уже целыми числами не обойтись
Вам понадобится:
- Линейка
- Умение проводить элементарные арифметические операции
#1
Отрезок – геометрическое место точек, находящихся на одной прямой и заключенных в пределах его концов. Концами отрезка являются точки. Отрезок является замкнутым множеством, следовательно, можно определить его размер. Мерой размера для отрезка является его длина. Вычислить длину отрезка можно точно и приблизительно. Для приблизительного вычисления необходимо использовать подручные средства. Как найти длину отрезка используя линейку? Достаточно приложить начало линейки к началу отрезка и посмотреть на какой цифре кончается отрезок. Это и будет его длина. Но следует учесть некоторые нюансы: . Длину отрезка невозможно абсолютно точно вычислить. . Масштабы и единицы измерения могут не совпадать
#2
Но как найти длину отрезка с высокой или абсолютной точностью? Для пространства каждой размерности существуют свои формулы. Рассмотрим простейший, одномерный случай. Декартовой системой для одномерного случая является обыкновенная координатная прямая. В реальной жизни мы сталкиваемся с сотнями примеров различных координатных прямых. Это и линейки, и строительные рулетки, и лента портного и даже трасса, где каждый километр отмечен порядковым номером. Нет ничего проще, чем измерить отрезок в одномерном пространстве. Особо легко, если начало отрезка совпадает с началом отсчёта (нулём) координатной прямой. В таком случае его длина будет совпадать с модулем координаты его конца. К примеру: если отрезок выходит из нуля, а конец его имеет координату 5, то длина отрезка будет равна пяти.
#3
Также нет задачи легче, чем как сравнить два отрезка, исходящих из нуля. Больше будет тот отрезок, модуль чьей координаты будет большим. Например: из нуля на координатной плоскости в разные стороны выходят два отрезка. Координата отрезка, выходящего влево равна -7, а выходящего вправо – 4. Модуль первого отрезка равен 7 со знаком “+” , а модуль второго – 4 с тем же знаком. Следовательно первый отрезок длиннее второго. Если отрезок начинается не в нуле, тогда следует пользоваться универсальной формулой вычисления длины для одномерного пространства. Звучит она следующим образом: “Для того чтобы найти длину отрезка в одномерном пространстве необходимо из значения координаты правого конца вычесть значение координаты левого конца”.
#4
Задача схожа с тем, как найти координаты середины отрезка, только в нашем случае координаты вычитаются, а не складываются и делятся пополам. Рассмотрим пример. Пусть отрезок имеет начало в точке 2, а конец в точке 11. Найти длину отрезка. Для этого вычтем из правой координаты значение левой: 11-2 = 9. Ответ: 9. Следует отметить, что можно наоборот, вычитать координату правого конца из левого, но тогда придётся брать результат по его абсолютному значению (модулю) . 2-11 = -9. Модуль -9 равен 9. Результат не изменился. Такой приём может помочь в решении специальных задач. Также следует рассмотреть примеры для двумерного пространства.
#5
Для двумерного пространства существуют специальные формулы, которые являются обобщением одномерного случая. Сразу рассмотрим конкретный пример, по пути решения объясняя формулы. Для её решения необходимо знать как называется отрезок, соединяющий 2 точки окружности. Такой отрезок называется хордой. Дана хорда с концами А (1;1) и B (4;5) . Найти длину отрезка AB. Длина отрезка АВ будет равна арифметическому квадратному корню из суммы квадратов разностей соответствующих координат точек. Эта форму выводится из теоремы Пифагора. Теперь по порядку. Чтобы найти разность соответствующих координат необходимо из x-координаты точки В вычесть x-координату точки А. Получим 4-1 = 3. Проводим такую же операцию и для y-координаты. Получим 5-1 = 4. Теперь каждую полученную разность возводим в квадрат: 3*3=9,4*4=16. Полученные результаты складываем: 9+16=25. Далее извлекаем квадратный корень. Корень из 25 = 5. Ответ: длина АВ = 5.
Алгебра
7 класс
Урок № 11
Длина отрезка. Координатная ось
Перечень вопросов, рассматриваемых в теме:
• Действительное число как мера длины отрезка.
• Координатная ось.
• Точки с действительными координатами на числовой оси.
• Сравнение действительных чисел на числовой оси.
Тезаурус:
Измерение длины отрезка – это сравнение длины отрезка с выбранной единицей измерения.
Длиной отрезка называется положительная величина, определённая для каждого отрезка. Любой отрезок имеет определённую длину, большую нуля.
Для каждого положительного действительного числа существует отрезок, длина которого выражается этим числом.
Отрезок, принятый за единицу измерения, называется единичным отрезком.
Прямую, на которой выбрано начало отсчета, положительное направление и единичный отрезок, называют координатной осью.
Координатой точки Р, лежащей на оси Ох, называется действительное число х = ±ОР, взятое со знаком «плюс», если точка Р лежит на положительной полуоси, и со знаком «минус», если эта точка лежит на отрицательной полуоси (где ОР означает длину отрезка ОР).
Основная литература:
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
Дополнительная литература:
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Длина отрезка
Рассмотрим несколько примеров измерения длины отрезка.
За единицу измерения возьмём 1 дм.

Длина отрезка АВ = 2 дм

Это значит, что на отрезке АВ укладывается ровно 2 дм.
Пусть длина отрезка АВ будет > 2дм, например, 2,1 дм

Пусть следующий отрезок имеет длину 2,14 дм.
Можно указать, что длина отрезка АВ ≈ 2,1дм с точностью до 0,1дм с недостатком.

Далее можно рассматривать отрезок
АВ ≈ 2,14 дм с точность до 0,01 и т.д.
В таких случаях длина отрезка АВ может быть выражена приближённо. Точное значение длины отрезка АВ выражается бесконечной десятичной дробью: AB = a0, a1, a2, a3… Говорят, что отрезок AB имеет длину a, где a = a0, a1, a2, a3…
Подведём итог.
Если задан единичный отрезок, то произвольный отрезок АВ имеет длину, равную некоторому положительному действительному числу а.
Верно обратное утверждение:
если задано любое положительное действительное число а, то можно указать отрезок АВ, длина которого равна этому числу.
Координатная ось
Далее зададим прямую, на которой выбрано положительное направление, начальная точка отсчета О и единичный отрезок.
Её называют координатной осью.

Точка О делит координатную ось на два луча. Один из них, идущий от точки О в положительном направлении, называют положительной полуосью, другой – отрицательной полуосью.
Каждой точке координатной оси поставим в соответствие действительное число х по следующему правилу:
начальной точке поставим в соответствие число ноль;
точке А, если она находится на положительном луче, поставим в соответствие число х, равное длине отрезка ОА.
Точке В, если она находится на отрицательном луче, поставим в соответствие отрицательное число х, равное длине отрезка ОВ, взятой со знаком «–».

На рисунке изображена координатная ось ОХ, где О – начало отсчёта.
Таким образом,
• каждой точке оси соответствует действительное число – координата этой точки;
• две различные точки А и В оси имеют разные координаты х1 и х2;
• каждое действительное число есть координата некоторой точки оси.
Это означает, что установлено взаимно – однозначное соответствие между точками оси и действительными числами.
Замечание: ранее на координатной прямой нами рассматривались точки, имеющие рациональные координаты. Теперь каждой точке соответствует действительное число.
Разбор решения заданий тренировочного модуля
Задача 1. Длина отрезка
Дано: А (2,6), В (-3,8)
Найдите: длину АВ, координату точки С – середины АВ.
Решение:

1. Чтобы найти длину отрезка надо из большей координаты вычесть меньшую, т.е. 2,6 – (-3,8) = 2,6 + 3,8 = 6,4
2. Чтобы найти координаты середины отрезка, надо сложить координаты и разделить на 2, т.е. (-3,8 +2,6) : 2 = -1,2 : 2 = -0,6.
Ответ: АВ = 6,4; С(-0,6).
Задача 2. Координатная ось.
Дано: на координатной оси расположены точки a, b, c.
Сравните:
1) a и b
Число a больше b, т.к. оно правее.
2) c – a и 0
Число c меньше a, значит, разность отрицательная, т.е.
c – a< 0
3) b • c и 0
Числа b и c отрицательные, значит, их произведение – число положительное, т.е. b • c > 0.
