Как найти длину отрезков разными способами

Длина отрезка

Отрезок — это геометрическая фигура, которая имеет начало и конец, значит отрезки можно измерять.

Измерить отрезок — значит найти его длину (расстояние между его концами).

Для того, чтобы найти длину отрезка, его сравнивают с отрезком принятым за единицу измерения, который носит название единичный отрезок.

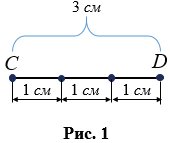
Если за единицу измерения принять сантиметр, то, чтобы определить длину отрезка, нужно узнать сколько раз в этом отрезке укладывается сантиметр. На рис.1 в отрезке СD сантиметр укладывается ровно три раза, значит, длина отрезка СD равна 3 см, можно записать СD = 3 см. В данном случае, для измерения удобно использовать сантиметровую линейку.

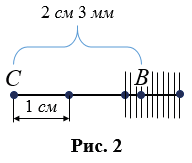
Бывает, что единичный отрезок не укладывается целое число раз в измеряемый отрезок, тогда единичный отрезок делят на 10 равных частей и определяют сколько раз одна десятая часть укладывается в остатке измеряемого отрезка. На рис.2 в отрезке СВ сантиметр укладывается 2 раза и в остатке 3 раза укладывается одна десятая часть сантиметра, значит, длина отрезка СВ равна 3,3 см или, учитывая что для сантиметра десятая часть равна миллиметру, 3 см 3 мм, т.е. можно записать СВ = 3,3 см (СВ = 3 см 3 мм).

Может получится так, что и в миллиметрах остаток не укладывается целое число раз, тогда:

• Если нужны более точные измерения, то процесс деления продолжается, т.е. миллиметр также можно разделить на 10 равных частей и т.д. Такая точность в повседневной жизни не нужна, поэтому пользуются приближенными значениями, но имеет важную роль при проведении каких-либо исследований для совершения научных открытий.

За единицу измерения можно принимать не только сантиметр, но и другие отрезки, например, дециметр, метр и т.д.

Длина отрезка — это всегда какое-то положительное число.

Свойства длин отрезков:

1. Равные отрезки имеют равные длины.
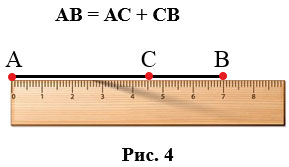
2. Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих двух отрезков. Так на Рис.4 точка С делит отрезок АВ на два отрезка АС и СВ. Приложим линейку и видим, что АС = 4,5 см, СВ = 2,5 см, АВ = 7 см, т.е. АС + СВ = АВ.

1. Если длина одного отрезка MN в n раз больше длины другого отрезка PQ, то записываютMN = nPQ. На Рис.5 даны два отрезка MN и PQ, приложим к ним линейку и видим, что MN = 8 см, PQ = 2 см, т.е. MN больше PQ в 4 раза, тогда можно записать, что MN = 4PQ.

Поделись с друзьями в социальных сетях:

Источник

Узнай длину каждого отрезка. Какой из них длиннее и на сколько сантиметров? Решить задачу разными способами.

Ответ или решение 1

Нам дан рисунок на котором изображены два отрезка http://bit.ly/2BiFMZ3 красный и зеленый. Нужно найти длины отрезков и на сколько один отрезок длиннее второго разными способами.

Чтобы решить задачу будем действовать по следующему алгоритму действий

• на рисунке помимо отрезков изображена еще и линейка, с помощью нее мы можем ответить на вопрос какая длина красного отрезка;
• вторым шагом мы можем с помощью линейка найти на сколько длина красного отрезка больше длинны зеленого;
• третьим шагом зная длину красного отрезка и на сколько зеленый отрезок меньше красного мы можем найти длину зеленого отрезка;
• второй способ решения задачи измерить длину двух отрезков, а затем найти на сколько один отрезок длиннее второго.

Узнаем длины отрезков и на сколько один отрезок длиннее второго

Первый способ решения задачи.

Смотрим на рисунок и определяем длину красного отрезка. Она равна 10 см.

Длину зеленого отрезка вычислить сложнее, так как его начало не совпадает с началом числового луча.

Зато мы можем сна рисунке увидеть на сколько красный отрезок длиннее зеленого.

Смотрим на рисунок и видим, что эта разница в длинах равна 3 см.

Теперь мы можем легко найти длину зеленого отрезка. Для этого из длины красного отрезка вычтем разницу в длинах красного и зеленого отрезков и получим длину зеленого отрезка.

10 см — 3 см = 7 см длина зеленого отрезка.

Второй способ решения задачи.

Длинна красного отрезка видна с рисунка и равна 10 см, берем линейку и меряем длину зеленого отрезка — он равен 7 см.

Разница в длине: 10 см — 7 см = 3 см.

Ответ: красный отрезок 10 см, зеленый отрезок 7 см, разница в длине 3 см.

Источник

Как узнать на сколько сантиметров один отрезок длиннее другого, разными способами

Ответ или решение 2

Рассмотрим варианты определения разности длины отрезков.

Первый способ

Предположим, что у нас имеют два отрезка, каждый из которых имеет свою длину. Наша задача определить определить на сколько сантиметров один из отрезков больше другого.

определяемся с отрезками и первым способом решения:

• первый отрезок имеет длину X см и он больше второго отрезка;
• второй отрезок имеет длину Y cм и он меньше первого отрезка;
• нужно определить на сколько см первый отрезок больше второго.

В результате решением будет: X-Y= Z, где Z это величина в сантиметрах на которую первый отрезок больше другого. И характерность этого способа в том, что мы узнавали насколько именно сантиметров первый отрезок длиннее второго.

Второй способ

Второй способ также подразумевает наличие двух отрезков разной длинны. Но во втором способе нашей задачей будет определение длины отрезка, который нужно добавить до величины второго отрезка, чтобы достичь длины первого отрезка

В этом способе решение будет выглядеть как: Y+Z=X

Разница способов заключается в подходе, который зависит от условия задачи. Если нужно определить, на сколько один отрезок больше другого, мы пользуемся первым способом. Если нужно определить, какой длинны отрезок нужно добавить до второго отрезка, чтобы получить первым, тогда мы используем второй способ.

Оба способа одинаково хороши и отличаются лишь акцентом в задаче, который изначально ставиться для задания пути желаемого решения. В обеих случаях используется одинаковый логический подход, одна общая формула.

Способ 1. Необходимо измерить длину каждого отрезка, а затем вычислить их разность математическим способом.

Способ 2. Нужно совместить начала отрезков (при этом они должны располагаться на одной прямой) и измерить расстояние от конца одного отрезка до другого.

Источник

Урок 3 Бесплатно Отрезок. Длина отрезка

Начнем знакомство с одним из разделов математики, который называется геометрия.

Слово геометрия древнегреческого происхождения, оно означает «землемерие» («гео» — земля, «метрео» — измерять).

Геометрия — древняя наука, возникла в результате практической деятельности человека: строительства зданий и дорог, установления земельных наделов и определения их размеров.

Становление данной науки происходило тысячелетиями.

В настоящее время геометрия — наука, занимающаяся изучением геометрических фигур, их свойствами, размерами и преобразованиями.

Сегодня обратим внимание на основные, базовые геометрические фигуры, такие как точка и отрезок.

Узнаем, что называют ломаной линией, какие геометрические фигуры называют многоугольниками, рассмотрим их основные элементы и характеристики.

Научимся сравнивать, находить длины отрезков.

Познакомимся с различными единицами измерения отрезков.

Рассмотрим свойства измерения длин отрезков.

Отрезок

Геометрическая фигура- это математическая модель, в которой рассматривается только форма и размер, не обращая внимания на иные свойства и состояния (цвет, из какого материала изготовлены, в каком состоянии находятся).

Как здания складываются из кирпичиков, так и сложные геометрические фигуры состоят из базовых фигур.

Одной такой элементарной фигурой является точка.

Точка — это неделимая фигура, не имеет частей и размеров (высоты, радиуса, длины и т.д.), направления и других характеристик.

В реальности моделью, которая дает представление о точке может стать, например, след, оставленный острием карандаша, или отверстие на бумаге от швейной иглы.

Слово «точка» с латинского языка означает мгновенное касание, укол.

Точку принято рассматривать как некоторое место в пространстве или на плоскости.

Принято обозначать точки заглавными латинскими буквами (А, В, С и т.д.).

Две точки на плоскости можно соединить бесконечным множеством линий.

Самой короткой линией, соединяющей две точки на плоскости, будет прямая, проведенная по линейке через эти две точки.

Кратчайшая линия между двумя точками называется отрезком.

Любые две точки можно соединить только одним отрезком.

Отрезок — это часть прямой линии, ограниченной двумя точками.

Точки, ограничивающие отрезок, называются концами отрезка.

Отрезок обозначают указанием имен его концов.

Через точки А и В с помощью линейки провели прямую.

А и В — концы отрезка.

Так как отрезок обозначают именами точек, получим отрезок АВ или ВА.

Пишут и говорят так: «Отрезок АВ» или «Отрезок ВА».

В названии отрезка не важно в каком порядке указываются его концы.

Отрезок АВ и ВА — это один и тот же отрезок.

Отрезок можно построить с помощью линейки.

Для этого необходимо к отмеченным на плоскости точкам приложить линейку и провести прямую от одного конца отрезка до другого.

Чтобы с помощью линейки начертить отрезок, который длиннее чем сама линейка, нужно поступить следующим образом:

Между точками А и В отметить точку С.

Затем передвинем линейку так, чтобы левый конец линейки оказался около точки С, по правому концу линейки отложим точку D.

Последовательно соединив концы отрезков, получится отрезок AD, который длиннее, чем линейка.

У меня есть дополнительная информация к этой части урока!

Давайте разберемся, как могут располагаться точки по отношению к отрезку:

1. Точка лежит на отрезке.

Говорят: «Точка G принадлежит отрезку ».

Записывают это так: G ∈ AB

2. Точка не лежит на отрезке.

Говорят: «Точка не принадлежит отрезку ».

Записывают это так: R ∉ AB

Пройти тест и получить оценку можно после входа или регистрации

Длина отрезка

Каждый отрезок имеет определенную длину, значение которой является числом.

Длина в геометрии — это величина, которая характеризует протяженность.

Длина отрезка — это расстояние между концами отрезка.

Так как каждый отрезок имеет длину, отрезки можно измерять и сравнивать.

Существует несколько способов сравнения отрезков.

1. Приблизительный способ сравнения.

Данный способ сравнения применяют только в том случае, когда длины отрезков явно отличаются.

Пример: Даны два отрезка АВ и ЕР

Очевидно, что отрезок АВ длиннее отрезка ЕР, значит, АВ > ЕР

2. Совмещение отрезков — более точный способ сравнения отрезков.

Метод заключается в следующем: совмещаются два отрезка друг с другом так, чтобы совпали их концы с одной стороны.

По расположению других концов относительно друг друга можно оценить какой из отрезков длиннее, а какой короче.

Если при наложении отрезков друг на друга длины отрезков совпадут, то отрезки равны (отрезки в этом случае будут равными фигурами).

Если при наложении отрезков друг на друга один из отрезков будет составлять часть второго, то первый отрезок является короче второго (т.е. длина первого меньше длины второго).

Пример: Даны два отрезка АВ и ОЕ

Сравним данные отрезки методом совмещения отрезков.

Совместим левый конец А отрезка АВ и левый конец О отрезка ОЕ.

Можно заметить, что отрезок ОЕ составляет часть отрезка АВ.

Значит, отрезок ОЕ короче отрезка АВ.

Данный метод удобен, если есть возможность перемещать отрезки, совмещать один с другим.

3. Сравнение отрезков с помощью измерителя.

Если нет возможности перемещать сравниваемые отрезки, то можно использовать промежуточный измеритель.

В математике для этих целей используют специальный чертежный инструмент, который называется циркулем.

Чтобы сравнить отрезки с помощью циркуля, необходимо совместить концы отрезка с ножками циркуля.

Не меняя раствор циркуля, приложить его ко второму отрезку и сравнить.

1. Если ножки циркуля совпадают с концами сравниваемого отрезка, то отрезки считаются равными.
2. Если отрезок выходит за пределы расставленных ножек циркуля, то он больше исходного отрезка.
3. Если же отрезок находится между концами измерителя, то сравниваемый отрезок меньше исходного.

Если нет возможности сравнить отрезки наложением и нет циркуля под рукой, то в качестве измерителя можно использовать нитку.

В таком случае нужно нитку приложить к исходному отрезку, на нитке по отрезку сделать замер, затем нитку приложить ко второму отрезку, оценить расположение замера на нитке по отношению к исследуемому отрезку, сделать вывод.

Пусть даны три отрезка СD, АЕ, BG

Сравним эти отрезки с помощью циркуля.

Соединим ножки циркуля с концами С и D отрезка СD.

Приложим циркуль с заданным раствором к отрезку АЕ.

Концы измерителя совпали с точками отрезка АЕ, значит, отрезки CD и AE равны: (CD = AE).

Приложим циркуль с заданным раствором к отрезку BG.

Отрезок выходит за концы измерителя, т.е. является частью отрезка BG, следовательно, отрезок BG длиннее отрезка СD: (BG > СD).

Все рассмотренные способы сравнения длины отрезков проводят без определения значения длины сравниваемых отрезков.

4. Существует еще один способ сравнения длины отрезков путем измерения их длинны.

Для этого необходимо сначала измерить длину каждого отрезка, далее сравнить полученные значения их длины и сделать вывод.

Большим будет являться тот отрезок, длина которого больше.

Соответственно, если длины измеряемых отрезков равны, то и отрезки равны.

У меня есть дополнительная информация к этой части урока!

Ломаная линия

Если последовательно соединить отрезки так, чтобы конец одного отрезка являлся началом следующего (при этом соседние отрезки не лежат на одной прямой), то образуется геометрическая фигура, которая называется ломаной линией.

Отрезки, из которых состоит ломаная линия, называют звеньями.

Концы отрезков называют вершинами ломаной.

Самые крайние вершины ломаной называют концами ломаной

Обозначение ломаной линии составляют из названий вершин этой ломаной, называя их по порядку.

Длиной ломаной называется сумма длин всех ее звеньев.

На рисунке изображена ломаная линия АBCDE.

Вершины ломаной АBCDE: А, B, C, D, Е.

Звенья ломаной АBCDE: AB, BC, CD, DE.

A и E — концы ломаной.

Найдем длину ломаной АВСDE:

АВСDE = AB+ BC+ CD+ DE = 2 см + 3 см + 4 см + 5 см = 14 см

Ломаная, концы которой совмещаются, называется замкнутой.

Многоугольником называется фигура, ограниченная замкнутой ломаной линией, звенья которой не пересекаются.

Отрезки (звенья) ломаной линии называют сторонами многоугольника.

Общие точки двух отрезков (сторон) многоугольника называют его вершинами.

Каждая пара сторон многоугольника, сходящиеся в одной точке, образуют углы многоугольника.

Количество сторон и количество углов в многоугольнике совпадают.

Вершины, стороны и углы многоугольника обозначаются аналогично ломаной линии.

Многоугольник принято обозначать и называть по его вершинам, начиная с любой вершины и называя их последовательно, в любом порядке.

На рисунке изображен многоугольник АBCDEF.

Вершины многоугольника АBCDEF: А, B, C, D, Е, F.

Стороны многоугольника АBCDEF: AB, BC, CD, DE, EF, FA.

Любые многоугольники можно сравнить: два многоугольника называются равными, если они совпадают при наложении.

Зная длину каждой стороны многоугольника, можно найти периметр этого многоугольника.

Периметр многоугольника — это сумма длин всех сторон.

Периметр многоугольника принято обозначать заглавной латинской буквой Р

Найдем периметр многоугольника АBCDEF (изображенного на рисунке):

Р_АВСDEF = AB+ BC+ CD+ DE+ EF+ FA = 2 см + 3 см + 2 см + 2 см + 3 см + 2 см = 14 см.

Существует огромное множество различных видов многоугольников.

Обычно многоугольники различают по числу сторон и углов.

Например: пятиугольник имеет 5 углов и 5 сторон, шестиугольник — 6 углов и 6 сторон.

Многоугольник с наименьшим числом вершин, сторон и углов называют треугольником.

Треугольник — плоская геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих эти точки.

Треугольник часто обозначают символом «Δ» и тремя заглавными латинскими буквами, которые обозначают его вершины.

На рисунке изображен треугольник АBC (Δ АBC).

А, В, С — вершины треугольника АBC.

Отрезки AB, BC, АC— стороны треугольника АBC.

Периметр треугольника- это сумма длин трех его сторон.

Найдем периметр треугольника АBC (изображенного на рисунке):

Р_АВС = AB+ BC+ АС = 4 см + 6 см + 3 см = 13 см.

Пройти тест и получить оценку можно после входа или регистрации

Источник

• 24
  

  Окт 16

• 

Узнай на сколько сантиметров один отрезок длиннее другого разными способами?

Узнай на сколько сантиметров один отрезок длиннее другого разными способами.

1 см это две клетки пошетать клетки и если клеток 10 то на 5 см.

На этой странице находится вопрос Узнай на сколько сантиметров один отрезок длиннее другого разными способами?, относящийся к категории Математика. По уровню сложности данный вопрос соответствует знаниям учащихся 1 — 4 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Математика. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

Лови бро все расписано.

Пусть х деталей бригада изготовила за 1 неделю. Тогда за 2 неделю было изготовлено 3х деталей. Зная, что за две недели было изготовлено 356 деталей, составим уравнение. Х + 3х = 356 4х = 356 х = 356÷4 х = 89 Ответ : за 1 неделю было изготовлено 89..

X деталей — изготовлено за первую неделю ; 3x деталей — изготовлено за вторую неделю. Составляем уравнение : x + 3x = 356 ; 4x = 356 ; x = 356 / 4 = 89(деталей). Ответ : за первую неделю изготовлено 89 деталей.

4800 * 74 — (506 — 399) * 301 + 30075 : 15 * 42 = 407203.

Х — трехместные лодки 6 — х — двухместные 3х + 2(6 — х) = 14 3х + 12 — 2х = 14 х = 14 — 12 х = 2 (лодки) трехместные 6 — 2 = 4 (лодки) двухместные.

Т. к. DM||KH, то расстояние от точки D до плоскостиα равно расстоянию от точки Н до прямой DM, высоте треугольника DMH к гипотенузе. HO = DH * HM / DM. DH = 4, HM = 3, DM = 5. HO = 4 * 3 / 5 = 2. 4. Чертеж и ход решения в файле.

108 * 55 / 297 = 20 108 * 55 = 5940 5940 / 297 = 20 2838 / 86 * 204 = 6732 2838 / 86 = 33 33 * 204 = 6732 245 + 315 — 28 * 15 = 140 28 * 15 = 420 245 + 315 = 560 560 — 420 = 140 (1237 + 108 — 126) * 61 = 74359 1237 + 108 = 1345 1345 — 126 = 1219 1219..

10кг = 10000г 10000 / 150 = 66(ост. 100) Ответ : 100г осталось нерасфасованным, 66 пачек получилось.

Нам надо найти сколько всего учащихся в школе, то есть 100% 45% = 180 100% = x x = 100% * 180 : 45% x = 400 (учеников) всего Ответ : В школе 400 учеников.

Узнай, на сколько сантиметров один отрезок длиннее другого, не измеряя их.

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Как узнать на сколько сантиметров один отрезок длиннее другого, разными способами

Рассмотрим варианты определения разности длины отрезков.

Первый способ

Предположим, что у нас имеют два отрезка, каждый из которых имеет свою длину. Наша задача определить определить на сколько сантиметров один из отрезков больше другого.

определяемся с отрезками и первым способом решения:

• первый отрезок имеет длину X см и он больше второго отрезка;
• второй отрезок имеет длину Y cм и он меньше первого отрезка;
• нужно определить на сколько см первый отрезок больше второго.

В результате решением будет: X-Y= Z, где Z это величина в сантиметрах на которую первый отрезок больше другого. И характерность этого способа в том, что мы узнавали насколько именно сантиметров первый отрезок длиннее второго.

Второй способ

Второй способ также подразумевает наличие двух отрезков разной длинны. Но во втором способе нашей задачей будет определение длины отрезка, который нужно добавить до величины второго отрезка, чтобы достичь длины первого отрезка

В этом способе решение будет выглядеть как: Y+Z=X

Разница способов заключается в подходе, который зависит от условия задачи. Если нужно определить, на сколько один отрезок больше другого, мы пользуемся первым способом. Если нужно определить, какой длинны отрезок нужно добавить до второго отрезка, чтобы получить первым, тогда мы используем второй способ.

Оба способа одинаково хороши и отличаются лишь акцентом в задаче, который изначально ставиться для задания пути желаемого решения. В обеих случаях используется одинаковый логический подход, одна общая формула.

Открытый урок 1вкласс . Учитель:  Андреева
Л.В.

Тема: Измерение длины
отрезка.

Цель урока:

-познакомить учащихся с понятием
мерка-единица измерения длины отрезка,

-установить общий принцип измерения
величин на примере измерения длин отрезков,

-познакомить с различными
старинными единицами измерения длины

Задачи:

-научить измерять и сравнивать
отрезки с помощью различных мерок,

Развивать практические умения,
интеллектуальные и коммуникативные умения, математическую речь,

Воспитывать у учащихся отношения
делового сотрудничества

Планируемые
результаты (целевые установки)

Предметные
—
усвоить понятие мерка; измерять длину отрезка различными мерками;
упорядочивать объекты по

длине
(на глаз, наложением, с использованием мерок); сравнивать длины отрезков на
глаз, с помощью полоски бумаги, общей мерки.

Метапредметные:

(Р)
—
формулировать цель, осознавать и сохранять учебную задачу; оценивать результаты
своей деятельности (чертить отрезки и измерять их длины);

(П)
—
проводить сравнение и осуществлять анализ объектов, делать выводы;

(К)
—
включаться в диалог, в коллективное обсуждение; проявлять инициативу и
активность, интегрироваться в

группу
(пару) сверстников, проявлять стремление ладить с собеседниками, вежливо
общаться; признавать свои ошибки.

Тип урока: изучение нового

Методы работы на уроке:

по виду источника информации:
словесные (беседа на этапе самоопределения,  при подготовке к активной
познавательной деятельности, при анализе слов,  когда делают выводы).

-наглядные (при подготовке к активной
познавательной деятельности, на основном этапе)

-практические (соотнесение слов и схем)

по виду учебной деятельности: самостоятельная
работа  (работа с рисунками, геометрическими фигурами),

работа в парах , фронтальная работа .

Используемые технологии   сотрудничество,
проблемный диалог.

Оборудование: модели
геометрических фигур, мерки, интерактивная доска, презентация из электронного
приложения к учебнику для 1 класса по программе «Перспектива»,  птицы из
бумаги, конверты с лентами разной длины, учебник Математика 1класс, авторы:
Г.В.Дорофеев, Т.Н.Миракова, Москва «Просвещение» 2015г. Рабочая тетрадь на
печатной основе часть 1 авторы: Г.В.Дорофеев, Т.Н.Миракова, Москва
«Просвещение» 2016г , тетрадь в клетку.

Ход урока.

Этап урока; задачи	Деятельность учителя.	Деятельность обучающихся	УУД
1. Актуализация	Доброе утро, ребята! – К уроку готовы? -Вспомним пословицу : Не стыдно не знать, … -Мы продолжаем узнавать новое. – Ребята скажите, какое сейчас время года? -Поздняя осень. Совсем недавно в нашем школьном дворе был листопад, и всё было так красиво, вот и у нас на доске дерево. Кто узнал ?  Жаль листочки с него облетели, да прямо на ваши парты. -На дереве у нас число 6, а на листочках состав чисел 2-6.У кого листочек с составом числа 6, повесьте его на дерево. Остальные покажите на экранах, состав какого числа у вас. Молодцы справились. – Ребята у вас на листочках написано слово «и». Каким математическим знаком можно заменить? Как называется такое действие? Как называется выражение чисел? -Подул сильный ветер и сорвал все листья с веток . Но к нам прилетела гостья. Кто это ?  -Почему синичка не улетела в теплые страны? Синичка принесла вам задания в конвертиках. Посмотрите на свои парты. Откройте конверты. 2. Достаньте листы из конверта. У меня такой же лист на доске. -Назовите, что изображено  ? -Какие линии вы видите? Доска:                                                                                               ·                                                                 – Обведите плавной линией все элементы множества отрезков. – Что о них можете сказать об их длине? – Как вы это определили?  – Как ещё можно узнать длину отрезка? Достаньте из конвертов ленты. -А все ли они одинаковой длины? – Как вы их сравнили? – Верно, длину сравнивают на глаз, а если возможно, то и наложением друг на друга – Наложите ленты друг на друга и сравните их по длине? Какие они? -Сегодня на уроке эти ленты нам послужат для измерения длины отрезков. Это мерки которыми можно измерить длину наших отрезков. Произнесите хором « мерка».	Стыдно не учиться. Осень Береза. + Сложение Сумма Синичка. Она- не перелетная птица. Геометрические фигуры, линии,… Учащиеся рассматривают фигуры, высказываются и приводят доказательства: -Изображена прямая (у прямой линии нет концов). -Изображены отрезки (две точки, соединённые прямой). -Кривые: замкнутые и незамкнутые. Один длинный, второй средний и короткий На глаз Мы не знаем, затрудняемся Ленты Разные, На глаз и наложили друг на друга Короткие и длинные Хоровое проговаривание Мерка	Познавательные  Научится  перерабатывать полученную информацию: сравнивать и группировать математические объекты на основе существенных признаков Проводить аналогии между изучаемым материалом и собственным опытом.  Выделение  необходимой информации из ранее изученного материала Коммуникативные Умение выслушать партнёра, корректно исправить ошибки
2. Постановка учебной задачи	– Кто определит задачу нашего урока? -Сегодня на уроке мы будем учиться измерять отрезки разными способами в том числе и мерками, потому что тема нашего урока «Измерение длины отрезка»	Дети отвечают	Регулятивные Научится определять и формулировать цель деятельности на уроке с помощью учителя
3. Создание проблемной ситуации. Работа в парах (каждой паре предлагаются полоски – мерки разные по цвету и длине)	– Предлагаю поработать в парах. – Как я назвала ленты – которые вам принесла синица? – Измерим длину отрезка на листе . Каждый своей меркой. Как работать меркой? – Какой результат получился? Поменяйтесь мерками. Почему разные результаты? – С помощью мерки измерим  длину ствола дерева на доске.(один ученик -оранжевой меркой, второй-белой меркой) – Что можно сказать о длине ствола? – Почему результат разный? Дерево ведь одно? Чтобы результат был одинаковый, что необходимо соблюдать? Физ. минутка(дети выполняют движения) Скачет шустрая синица, Ей на месте не сидится, Прыг-скок,прыг-скок, Завертелась ,как волчок. Вот присела на минутку, Почесала клювом грудку, И с дорожки- на плетень, Тири-тири. Тень-тень-тень.	Мерки Разные мерки – Чтобы измерять длину, надо пользоваться одинаковыми мерками.	Коммуникативные учиться осуществлять взаимный контроль и оказывать в сотрудничестве необходимую помощь. Познавательные Проводить аналогии между изучаемым материалом и собственным опытом. Регулятивные УУД: принимать и сохранять учебную задачу и активно включаться в деятельность.
4. Закрепление. 4.1.Работа по учебнику (в парах). Практическая работа	Как измерить длину класса? 1 ребенок и учитель измеряют. Какие результаты получились? Посему? Оказывается, не только мы решаем эту проблему, в старину люди тоже искали различные (мерки) меры измерения.  Историческая справка. Единицы измерения длины. В старину русские меры длины были основаны на размерах разных частей тела человека. Электронное приложение 1 класс матем.к учебнику  Дорофеева Г.В. СЛАЙД «Старинные русские меры»: пядь, локоть, фут  и др -Удобно ли было пользоваться такими мерками? -Представим себе что мы попали в далёкое прошлое и нам нужно измерить длину верёвки пядью. Измерим пядью ширину парты. Кто же прав? Почему разная ширина? Почему? -Поэтому, было неудобно пользоваться такими мерками, из-за этого возникали споры и ссоры. -Чтобы у нас не возникли споры, мы, договоримся измерять наши отрезки клетками	Можно шагами. Шаги разные Разные руки у взрослого человека рука большая и пядь больше, чем у детей	Познавательные ориентироваться в учебнике; устанавливать причинно-следственные связи Регулятивные  высказывать своё предположение на основе работы с иллюстрацией учебника Коммуникативные уметь выражать в речи свои мысли и действия. Учиться  осуществлять взаимный контроль и оказывать в сотрудничестве необходимую помощь.
4.2.Работа в рабочей тетради	Откроем  рабочую тетрадь на странице 68 №2 -Как предлагают измерить длину отрезка? (посчитать клетки и записать справа длину отрезка) Вслух по цепочке с проговариванием выполняем задание. Почему результаты получились одинаковые?	Необходимо посчитать сколько вмещает клеточек каждый отрезок ВЕ=4 клетки, ГК=5клеток, ДН=9клеток, ИС=7клеток, МО=6кл,  ЛТ=1 клетка	Регулятивные УУД: принимать и сохранять учебную задачу. Познавательные Проводить аналогии между изучаемым материалом и собственным опытом.
4.3. Практическая работа в тетрадях в клетку (это же задание вынести на интерактивную доску)	А можно ли самим по клеткам начертить отрезки? -Поставим в тетради точку и начертим отрезок в 4 клетки, на конце опять поставим точку, (учитель выполняет задание на интерактивн. доске) -Начертим 2 отрезка длиной 4 клетки, 2 отрезка  длиной 2 клетки) -Посмотрите , что я сделать из этих отрезков? (учитель переносит отрезки на дерево и составляет из них кормушку) – Ну вот птичья столовая готова, осталось насыпать в неё корм.	Да (Выполнение задания в  тетради. От руки чертят по клеткам отрезки по клеткам)	Регулятивные  учиться самостоятельно адекватно оценивать правильность выполнения действия и вносить необходимые коррективы. Коммуникативные задавать вопросы; использовать речь для регуляции своего действия
5. Повторение. Решение примеров на знание состава числа от 5 до 7	Тетрадь с. 68 задания 3,4	1+1=2 5-1=4 3+1=4 6-1=5	Познавательные Применение знаний полученных на предыдущих уроках
6. Итог урока	–  Какие задачи мы ставили в начале урока? – А как можно найти длину отрезка? -На каких уроках пригодятся, вам, эти знания? -Где это может нам в жизни пригодиться?	Как можно измерить длину отрезка На глаз, меркой, по клеткам На уроках технологии При покупки длины материала, ленты, в магазине	Коммуникативные уметь выражать в речи свои мысли.
7. Рефлексия.Самооценка	-Ребята, что было сложным на уроке? Оцените свою работу на уроке: -Мне было интересно и всё понятно; -Мне было интересно, но ещё не всё понял; -Мне было непонятно и неинтересно.	Учащиеся высказываются.	Регулятивные УУД: учиться самостоятельно адекватно оценивать правильность выполнения действия

Самоанализ  урока  математики для 1 класса
по теме «Измерение длины отрезков».

Ф.И.О. учителя: Андреева
Л.В.

Класс 1в.

Предмет:
математика.

Дата поведения
: 14.11.19.

Программа «Перспектива»

Тема урока: «Измерение 
длины  отрезков».

Тип урока: Изучение
нового материала.

Место и роль урока в изучаемой теме: 1 урок
по теме «Длина и её измерение».

Цель урока:

-познакомить учащихся с понятием мерка-единица
измерения длины отрезка,

-установить общий принцип измерения
величин на примере измерения длин отрезков,

-познакомить с различными старинными
единицами измерения длины

Задачи:

-научить измерять и сравнивать отрезки с
помощью различных мерок,

Развивать практические умения,
интеллектуальные и коммуникативные умения, математическую речь,

Воспитывать у учащихся отношения делового
сотрудничества

В соответствии с типом урока предусмотрена
следующая структура его проведения:

1.     Организационное
начало урока.

2.     Актуализация

3.     Постановка
учебной задачи

4.     Создание
проблемной ситуации.

5.     Закрепление.

5.1. Работа по учебнику .
Практическая работа

5.2. Работа в рабочей
тетради

5.3.         
Практическая работа в тетрадях в клетку

6.     Повторение.
Решение примеров на знание состава числа от 5 до 7

7.     Итог
урока

8.     Рефлексия.

 Используемые методы обучения

Методы управления учебной деятельностью и
восприятия информации:

а) по источнику передачи и восприятия
информации – словесные, наглядные, практические;

б) по логике передачи и восприятия
информации – индуктивные и дедуктивные;

в) по степени самостоятельности учащихся –
репродуктивные и проблемно-поисковые;

г) по степени управления учебной
деятельностью – учебная деятельность, организованная и управляемая учителем,
самостоятельная деятельность уч-ся, работа с учебником.

 Методы контроля и самооценки:

а) фронтальная работа, опрос;

б) экспресс-опрос;

в) самоконтроль.

8. Планируемые результаты:

предметные: усвоить
понятие мерка; измерять длину отрезка различными мерками;
упорядочивать объекты по

длине
(на глаз, наложением, с использованием мерок); сравнивать длины отрезков на
глаз, с помощью полоски бумаги, общей мерки.

метапредметные:

 (Р) —
формулировать цель, осознавать и сохранять учебную задачу; оценивать результаты
своей деятельности (чертить отрезки и измерять их длины);

(П)
—
проводить сравнение и осуществлять анализ объектов, делать выводы;

(К)
—
включаться в диалог, в коллективное обсуждение; проявлять инициативу и
активность, интегрироваться в

группу
(пару) сверстников, проявлять стремление ладить с собеседниками, вежливо
общаться; признавать свои ошибки.

Универсальные учебные действия:

Личностные:
учебное сотрудничество с учителем и одноклассниками; ориентация на образец
поведения «хорошего ученика» как пример для подражания; осознание своих
возможностей в учении, способность адекватно судить о причинах своего
успеха/неуспеха в учении; уважать себя и верить в успех.

Регулятивные:
определять умения, которые будут сформированы на основе изучаемой темы,
определять круг своего незнания; определять цель урока, планировать свои
действия для реализации задач, прогнозировать результаты; осуществлять итоговый
и пошаговый контроль результатов; оценивать результаты собственной
деятельности, объяснять по каким критериям проводилась оценка.

Познавательные:
анализировать, сравнивать, группировать отвлеченные и именованные числа;
самостоятельно делать выводы, перерабатывать информацию, преобразовывать ее и
представлять информацию в виде схем.

Коммуникативные:
учитывать разные мнения и стремиться к координации различных позиций при работе
в паре, договариваться и приходить к общему решению.

Оборудование: компьютер,
мультимедийный проектор, презентация к уроку, учебник, тетрадь, конверты с
лентами-мерками, лист с изображениями разных линий.

    Данный урок разработан в соответствии
с требованиями, предъявляемыми к современному уроку в рамках реализации ФГОС,
рабочей программой по математике для 1 класса УМК «Перспектива».  Урок
разработан с учетом возрастных особенностей учащихся, в который включены
элементы современных педагогических технологий: здоровьесберегающей,
личностно-ориентированной, ИКТ, а именно: положительный эмоциональный настрой,
мотивация, развитие познавательного интереса, проведение физминуток, работа в
парах , использование компьютера, практическая работа, связь с жизнью.

     Такой урок способствует развитию
творческих способностей и личностных качеств: оценить самому роль знаний и
увидеть их применение на практике, это самостоятельность и совсем другое
отношение к своему труду. Нужно дать возможность научиться наблюдать, понимать,
успевать, систематически повторять и закреплять учебный материал, чтобы на
уроке справляться с предложенным объёмом учебного материала. Кроме того, в ходе
решения задач важным является не только сам факт выполнения задания, но и
выбранный учащимся способ решения. Существенным является умение ученика
максимально точно и выразительно излагать свои мысли. Для введения в тему урока
была предложена проблемная ситуация, с которой учащиеся успешно справились. На
уроке не забывала и о физическом здоровье детей: следила за осанкой, чередовала
виды деятельности, смена слайдов, проведена физкультминутка.

   Содержание урока соответствует теме и поставленным задачам и
целям. Все они реализованы в ходе урока.

   Вся деятельность учащихся была направлена на ознакомление с
новым приёмом измерения отрезков.

     При подборе материала опиралась на зону ближайшего развития,
стремилась к тому, чтобы при выполнении учебной задачи каждый ученик приложил
определённое доступное усилие, умел использовать в собственной деятельности
результаты коллективной работы и проявлял самостоятельность. Организация
учебной деятельности строилась таким образом, чтобы каждый ученик с помощью
учителя пытался ставить цели, добивался определённых успехов, стремилась
сделать каждого ученика соучастником научного поиска. Для этого использовались
различные методы и приёмы работы:

·        
частично –
поисковый метод при составлении алгоритма

·        
проблемный при
открытии нового знания

·        
аналитико –
синтетический

·        
самостоятельная
работа при проверке усвоения знаний.

·        
самоконтроль
при проверке самостоятельно выполненных заданий, при работе в парах.

На уроке происходила смена одного вида деятельности другим:

·        
устные упражнения
чередовались с письменными, использовались минутки отдыха

·        
применялись
различные формы организации деятельности учеников: фронтальная, индивидуальная,
работа в парах.

         Мотивационная часть.

Формирование познавательной мотивации происходило на основе
создания проблемной ситуации . Познавательная мотивация формировалась с опорой
на эмоциональную мотивацию (при знакомстве с планом работы через зрительное
восприятие, использование наглядности, компьютера. Заложена смена деятельности
детей: они слушают, думают, отвечают на вопросы.

       В течение урока ученики
класса находились в поле зрения учителя, все первоклассники были заняты. Урок
выдержан по времени, этапы распределен по минутам.  Дети были
заинтересованы изложенным материалом, т.к. это первый урок, когда они сами
рассмотрели материал и преподнесли его другим. Атмосфера в классе положительная,
доброжелательная. На уроке была активная работа учащихся.
Дети показывали умение работать под руководством учителя, самостоятельно
выполнять задания. Но, все-таки некоторая скованность
у ребят присутствовала, не все выложились на 100%.

        Мои взаимоотношения с учащимися на
уроке носили характер сотрудничества и взаимопонимания. Во время работы я дала
возможность ученикам высказывать своё мнение. Спорные высказывания старалась не
опровергать, а предлагать ученикам провести обсуждение. На протяжении урока
учила детей быть аккуратными и трудолюбивыми, соблюдать правила поведения на
уроке.

      Урок был проведён в достаточном
темпе. Всё запланированное на данный урок было осуществлено. На этапе подведения
итогов урока была проведена рефлексия.

       Урок достиг целей, что подтверждают
осознанные ответы учащихся на итоговые вопросы урока. Считаю, что задачи урока
были мною успешно реализованы, урок удался.

14.11.19. Учитель начальных классов       
           Андреева Л.В.