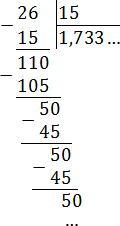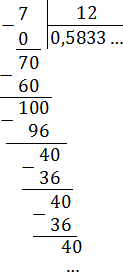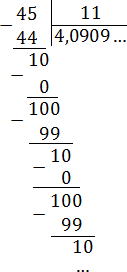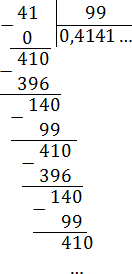Как найти длину периода десятичной дроби - Сайт, где вы сможете решить свои вопросы

Это очень просто

Время на прочтение
2 мин

Количество просмотров 19K

Рассмотрим следующую задачу. Найти период дроби 1/81. Уверяю, что для решения не потребуется ни калькулятор, ни деление столбиком. Для начала вспомним чему равно 81*(Период). Пусть длина периода n, тогда исходная дробь запишется как:

$frac{1}p=frac{Период}{10^n}+frac{Период}{10^{2n}}+frac{Период}{10^{3n}}+...$

Перепишем данное представление в следующем виде:

$frac{1}p=frac{Период}{10^n}+frac{1}{10^n} cdotleft(frac{Период}{10^{n}}+frac{Период}{10^{2n}}+..right)$

Последнее выражение можно представить так:

$frac{1}p=frac{Период}{10^n}+frac{1}{10^n} cdotfrac{1}p$

Ну а теперь то соотношение, которое мы искали:

Для нашего случая это тождество будет следующим:

Разделим левую и правую часть на 9, получим:

Первое число, составленное из одних единиц, которое делится на 9 равно 111111111, это следует из признака делимости на 9. Делить будем через сумму цифр исходного числа. Двигаемся слева направо, складываем цифры делимого и на каждом шаге записываем полученную сумму. Результат работы данного алгоритма — число 12345678,9999… Здесь надо пояснить, что когда мы достигаем крайней правой цифры, то ставим запятую и полученную сумму цифр исходного числа дублируем как бесконечную десятичную дробь. Вспоминаем, что 0,999…=1 и получаем ответ, который мы искали 12345679. Если рассмотреть более общую задачу нахождения периода дроби $frac{1}{9^n}$ , то окажется, что период такой дроби имеет длину ${9^{n-1}}$ и если известен период для случая n-1, то следующий равен произведению данного периода на число вида 11111… (повторяется ${9^{n-1}}$ раз)22222… (повторяется ${9^{n-1}}$ раз)33333… (повторяется ${9^{n-1}}$ раз). Самая правая секция будет иметь вид 8888..889. Последняя цифра девятка.
И еще одно наблюдение, теперь для дробей вида $frac{1}{11^{n}}$ . В этом случае длина периода равна $2cdot{11^{n-1}}$ . И если известен период для случая n-1, то следующий период равен произведению данного периода на число, составленное из 10 блоков, где длина каждого блока $2cdot{11^{n-2}}$ . Блоки имеют следующую структуру:
09090909…
18181818…
27272727…
36363636…
…
последний блок 90909091. Для $frac{1}{11}$ период 09, для $frac{1}{11^{2}}$ период будет 09182736455463728191*9=0082644628099173553719.
Проверил формулу для $frac{1}{11^{3}}$ . Получил

75131480090157776108189331329827197595792637114951164537941397445529676934635612
32156273478587528174305033809166040570999248685199098422238918106686701728024042
0736288504883546205860255447032306536438767843726521412471825694966190833959429,

что совпадает с периодом без ведущих нулей.

Приведу код процедур, которые я использовал для проверки своих выводов.

Function GreatestCommonDivisor(x,y)

    if x=y then
        return x;
    endif;  

    a=min(x,y);
    if a=1 then
        return 1;
    endif;  
    b=x+y-a;

    while TRUE do
     c=b%a; 
     if c=0 then
         return a;
     endif;  
     b=a;
     a=c;
    enddo;

EndFunction

Function NumeratorFractionPeriod(numerator,denumerator)

    // дробь a/b

    a=numerator;
    b=denumerator;

    while b%2=0 do
        b=b/2;
        a=a*5;
    enddo;  

    while b%5=0 do
        b=b/5;
        a=a*2;
    enddo;  
    //наибольший общий делитель
    c=GreatestCommonDivisor(a,b);
    a=a/c;
    b=b/c;

    if b=1 then
        Period=string(a);
        return Period;
    endif;

    if a>b then
        Period=string((a-a%b)/b);
        a=a%b;
        if a=0 then
            return Period;
        endif;  
        Period=Period+"(";
    else
        Period="(";
    endif;      

    while a%10=0 do
        a=a/10;
    enddo;  

    i=a;
    while TRUE do
        j=0;
        while i<b do
            i=i*10;
            j=j+1;
            if j>1 then
             Period=Period+"0";
            endif; 
        enddo;  

        check=i-a;
        if (check%b)=0 then
            Period=Period+(check)/b;
            break;
        else
            j=i%b;
            Period=Period+(i-j)/b;
            i=j;
        endif;    
    enddo;

    return Period+")";
EndFunction

Источник

Периодические десятичные дроби

10 февраля 2012

Помните, как в самом первом уроке про десятичные дроби я говорил, что существуют числовые дроби, не представимые в виде десятичных (см. урок «Десятичные дроби»)? Мы еще учились раскладывать знаменатели дробей на множители, чтобы проверить, нет ли там чисел, отличных от 2 и 5.

Так вот: я наврал. И сегодня мы научимся переводить абсолютно любую числовую дробь в десятичную. Заодно познакомимся с целым классом дробей с бесконечной значащей частью.

Периодическая десятичная дробь — это любая десятичная дробь, у которой:

Значащая часть состоит из бесконечного количества цифр;

Через определенные интервалы цифры в значащей части повторяются.

Набор повторяющихся цифр, из которых состоит значащая часть, называется периодической частью дроби, а количество цифр в этом наборе — периодом дроби. Остальной отрезок значащей части, который не повторяется, называется непериодической частью.

Поскольку определений много, стоит подробно рассмотреть несколько таких дробей:

Эта дробь встречается в задачах чаще всего. Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.

Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.

Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.

Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6. Для удобства повторяющиеся части отделены друг от друга пробелом — в настоящем решении так делать не обязательно.

Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.

Как видите, определение периодической дроби основано на понятии значащей части числа. Поэтому если вы забыли что это такое, рекомендую повторить — см. урок «Умножение и деление десятичных дробей».

Переход к периодической десятичной дроби

Рассмотрим обыкновенную дробь вида a/b. Разложим ее знаменатель на простые множители. Возможны два варианта:

В разложении присутствуют только множители 2 и 5. Эти дроби легко приводятся к десятичным — см. урок «Десятичные дроби». Такие нас не интересуют;
В разложении присутствует что-то еще, кроме 2 и 5. В этом случае дробь непредставима в виде десятичной, зато из нее можно сделать периодическую десятичную дробь.

Чтобы задать периодическую десятичную дробь, надо найти ее периодическую и непериодическую часть. Как? Переведите дробь в неправильную, а затем разделите числитель на знаменатель «уголком».

При этом будет происходить следующее:

Сначала разделится целая часть, если она есть;
Возможно, будет несколько чисел после десятичной точки;
Через некоторое время цифры начнут повторяться.

Вот и все! Повторяющиеся цифры после десятичной точки обозначаем периодической частью, а то, что стоит спереди — непериодической.

Задача. Переведите обыкновенные дроби в периодические десятичные:

Все дроби без целой части, поэтому просто делим числитель на знаменатель «уголком»:

Как видим, остатки повторяются. Запишем дробь в «правильном» виде: 1,733 … = 1,7(3).

В итоге получается дробь: 0,5833 … = 0,58(3).

Записываем в нормальном виде: 4,0909 … = 4,(09).

Получаем дробь: 0,4141 … = 0,(41).

Переход от периодической десятичной дроби к обыкновенной

Рассмотрим периодическую десятичную дробь X = abc(a₁b₁c₁). Требуется перевести ее в классическую «двухэтажную». Для этого выполним четыре простых шага:

Найдите период дроби, т.е. подсчитайте, сколько цифр находится в периодической части. Пусть это будет число k;
Найдите значение выражения X · 10^k. Это равносильно сдвигу десятичной точки на полный период вправо — см. урок «Умножение и деление десятичных дробей»;
Из полученного числа надо вычесть исходное выражение. При этом периодическая часть «сжигается», и остается обычная дробь;
В полученном уравнении найти X. Все десятичные дроби переводим в обыкновенные.

Задача. Приведите к обыкновенной неправильной дроби числа:

9,(6);

32,(39);

0,30(5);

0,(2475).

Работаем с первой дробью: X = 9,(6) = 9,666 …

В скобках содержится лишь одна цифра, поэтому период k = 1. Далее умножаем эту дробь на 10^k = 10¹ = 10. Имеем:

10X = 10 · 9,6666 … = 96,666 …

Вычитаем исходную дробь и решаем уравнение:

10X − X = 96,666 … − 9,666 … = 96 − 9 = 87;
9X = 87;
X = 87/9 = 29/3.

Теперь разберемся со второй дробью. Итак, X = 32,(39) = 32,393939 …

Период k = 2, поэтому умножаем все на 10^k = 10² = 100:

100X = 100 · 32,393939 … = 3239,3939 …

Снова вычитаем исходную дробь и решаем уравнение:

100X − X = 3239,3939 … − 32,3939 … = 3239 − 32 = 3207;
99X = 3207;
X = 3207/99 = 1069/33.

Приступаем к третьей дроби: X = 0,30(5) = 0,30555 … Схема та же самая, поэтому я просто приведу выкладки:

Период k = 1 ⇒ умножаем все на 10^k = 10¹ = 10;

10X = 10 · 0,30555 … = 3,05555 …
10X − X = 3,0555 … − 0,305555 … = 2,75 = 11/4;
9X = 11/4;
X = (11/4) : 9 = 11/36.

Наконец, последняя дробь: X = 0,(2475) = 0,2475 2475 … Опять же, для удобства периодические части отделены друг от друга пробелами. Имеем:

k = 4 ⇒ 10^k = 10⁴ = 10 000;
10 000X = 10 000 · 0,2475 2475 = 2475,2475 …
10 000X − X = 2475,2475 … − 0,2475 2475 … = 2475;
9999X = 2475;
X = 2475 : 9999 = 25/101.

Смотрите также:

Сравнение дробей
Тест к уроку «Десятичные дроби» (2 вариант)
Четырехугольная пирамида в задаче C2
Как сдать ЕГЭ по математике
Задача B5: площадь сектора
Задача B4: тарифы на сотовую связь

Источник

Период десятичной дроби. Онлайн калькулятор

Онлайн калькулятор нахождения периода десятичной дроби может вычислить период дроби, числителем и
знаменателем которой могут быть как целые числа, так и десятичные дроби.

Для записи десятичной дроби используйте точку либо запятую (например, 1.12 или 1,12). Обратите внимание, что калькулятор вычисления периода десятичной дроби находит период в пределах 30000 чисел, так как длина периода может достигать сотен тысяч символов и
вычисления займут большое количество времени.

Вам могут также быть полезны следующие сервисы

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор упрощения выражений

Калькулятор со скобками

Калькулятор уравнений

Калькулятор суммы

Калькулятор пределов функций

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Калькулятор делителей числа

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Калькулятор свойств корней и степеней

Калькулятор комплексных чисел

Калькулятор среднего арифметического

Калькулятор арифметической прогрессии

Калькулятор геометрической прогрессии

Калькулятор модуля числа

Калькулятор абсолютной погрешности приближения

Калькулятор абсолютной погрешности

Калькулятор относительной погрешности

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькулятор нахождения наименьшего угла

Калькулятор определения вида угла

Калькулятор смежных углов

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N₂ | Двоичная система счисления

N₃ | Троичная система счисления

N₄ | Четырехичная система счисления

N₅ | Пятеричная система счисления

N₆ | Шестеричная система счисления

N₇ | Семеричная система счисления

N₈ | Восьмеричная система счисления

N₉ | Девятеричная система счисления

N₁₁ | Одиннадцатиричная система счисления

N₁₂ | Двенадцатеричная система счисления

N₁₃ | Тринадцатеричная система счисления

N₁₄ | Четырнадцатеричная система счисления

N₁₅ | Пятнадцатеричная система счисления

N₁₆ | Шестнадцатеричная система счисления

N₁₇ | Семнадцатеричная система счисления

N₁₈ | Восемнадцатеричная система счисления

N₁₉ | Девятнадцатеричная система счисления

N₂₀ | Двадцатеричная система счисления

N₂₁ | Двадцатиодноричная система счисления

N₂₂ | Двадцатидвухричная система счисления

N₂₃ | Двадцатитрехричная система счисления

N₂₄ | Двадцатичетырехричная система счисления

N₂₅ | Двадцатипятеричная система счисления

N₂₆ | Двадцатишестеричная система счисления

N₂₇ | Двадцатисемеричная система счисления

N₂₈ | Двадцативосьмеричная система счисления

N₂₉ | Двадцатидевятиричная система счисления

N₃₀ | Тридцатиричная система счисления

N₃₁ | Тридцатиодноричная система счисления

N₃₂ | Тридцатидвухричная система счисления

N₃₃ | Тридцатитрехричная система счисления

N₃₄ | Тридцатичетырехричная система счисления

N₃₅ | Тридцатипятиричная система счисления

N₃₆ | Тридцатишестиричная система счисления

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка. Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Генератор Pdf с примерами

Тренажёры решения примеров

Тренажер по математике

Тренажёр таблицы умножения

Тренажер счета для дошкольников

Тренажер счета на внимательность для дошкольников

Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ.

Тренажер решения примеров с разными действиями

Тренажёры решения столбиком

Тренажёр сложения столбиком

Тренажёр вычитания столбиком

Тренажёр умножения столбиком

Тренажёр деления столбиком с остатком

Калькуляторы решения столбиком

Калькулятор сложения, вычитания, умножения и деления столбиком

Калькулятор деления столбиком с остатком

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Цифры в текст

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

Источник

This answer seeks to explain why Ross Millikan’s answer works, and provides further information on techniques to speed up the process of seeking the period:

Consider the fraction $frac17$. The decimal expansion of this is
$$
frac17 = 0.overline{142857}
$$
for a period of 6. Now consider what happens when we multiply it by $10^6$:
$$
10^6timesfrac17 = 142857.overline{142857}
$$
Subtracting the original fraction from this gives
$$
(10^6-1)timesfrac17 = 142857
$$
And so, we have
$$
frac17 = frac{142857}{10^6-1}
$$
As you can see, the denominator is one less than a power of 10, and the power is the period of the decimal expansion. This is no accident, and works for any fraction – if you can rewrite it in this form, the denominator reveals the period.

Now, rearrange the equation:
$$
10^6-1 = 142857times 7
$$
So $10^6$ must be one more than a multiple of 7 (or, more generally, $10^n$ must be one more than a multiple of $d$, where $d$ is the denominator of the fraction and $n$ is the period of the decimal expansion) – indeed, it must be the smallest power of 10 (larger than 1) that has this property.

As such, we can use modular arithmetic to look for the period. Since $atimes dequiv 0 pmod d$, we have that $10^n-1equiv0 pmod d$, or
$$10^n equiv 1pmod d$$
And therefore you can just look for the smallest $n>0$ satisfying this.

Of course, there are other approaches to gain the same result, but they’re all fundamentally variants of the same idea. That said, if you can factor $phi(d)$ – the euler totient function of the denominator – then you can accelerate the process of looking for the smallest $n$. For example, when checking 13, you have $phi(13)=12$, so $nin{1,2,3,4,6,12}$ (as these are the factors of 12) – this can save you a lot of computation (especially where $phi(d)$ has only a few large factors and 2).

For example, $phi(167)=166 = 2times83$, so $nin{1,2,83,166}$. Therefore, we need to check only these four, and we can do it quite efficiently. Obviously, neither $10$ nor $100=10^2$ are equivalent to 1 mod 167, so we only need to actually check 83. For this we can use binary exponentiation. Note that $83 = 2^6 + 2^4 + 2^1 + 2^0$. So we can write
$$begin{align}
10^{83} &= 10^{2times(2^5 + 2^3 + 1)}times 10\
&= (10^{2^3times(2^2+1)}times 10)^2 times 10\
&= ((10^{2^2}times10)^{2^3}times 10)^2 times 10
end{align}$$
So, working in modular arithmetic, we can go
$$begin{align}
10^{83} &equiv ((10^{2^2}times10)^{2^3}times 10)^2 times 10 mod 167\
&equiv ((100^2times 10)^{2^3}times 10)^2times10mod167\
&equiv ((147times 10)^{2^3}times 10)^2times10mod167\
&equiv (134^{2^3}times 10)^2times10mod167\
&equiv (87^{2^2}times 10)^2times10mod167\
&equiv (54^2times 10)^2times10mod167\
&equiv (77times 10)^2times10mod167\
&equiv 102^2times10mod167\
&equiv 50times10mod167\
&equiv 166mod167
end{align}$$
This is the same as $-1pmod{167}$, so $n=166$ is the only possible period, and $frac1{167}$ has a period of 166.

Also note that you don’t actually have to expand out the product like that. You can just write the number in binary ($83_{10} = 1010011_2$), then work through the binary digits left-to-right – start with 1, and for each digit, $b$, multiply by $10^b$. Square it after each digit except the last one.

Источник

Это очень просто

Периодические десятичные дроби

Переход к периодической десятичной дроби

Переход от периодической десятичной дроби к обыкновенной

Период десятичной дроби. Онлайн калькулятор

Вам также может понравиться

Как найти магазин механика

В норе маленькие лису лисята ждали как правильно предложение составить

Как найти монтажников кондиционеров

Добавить комментарий Отменить ответ