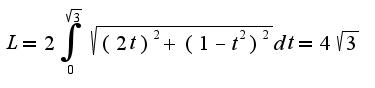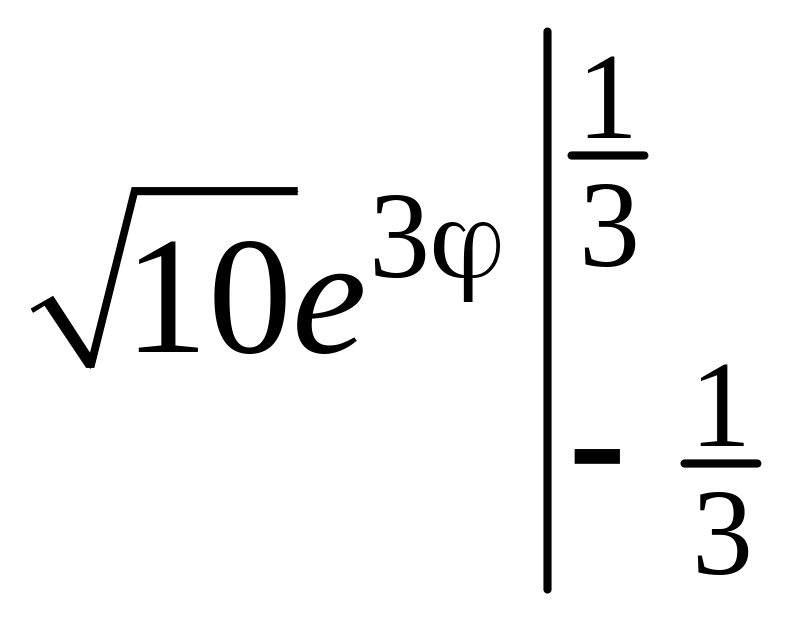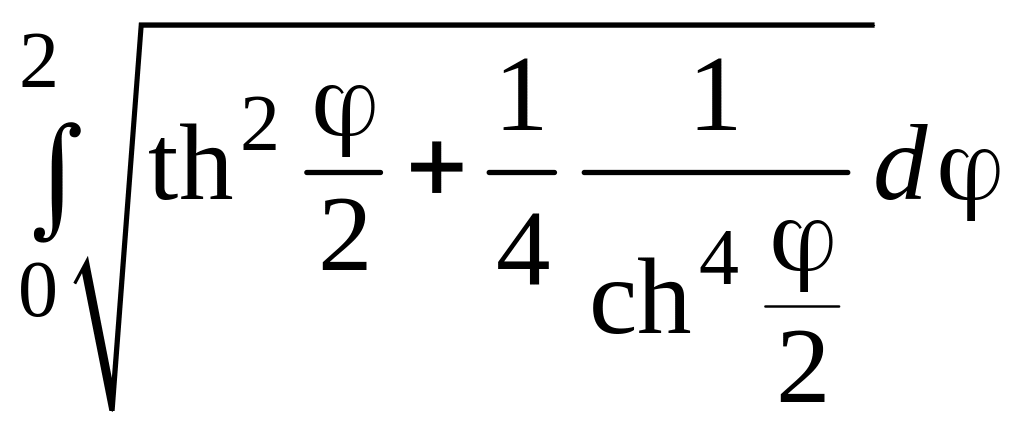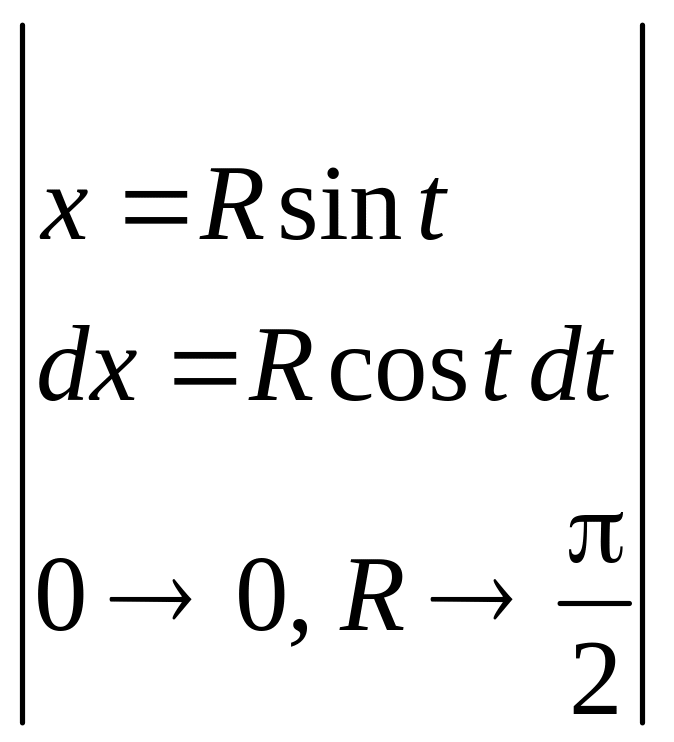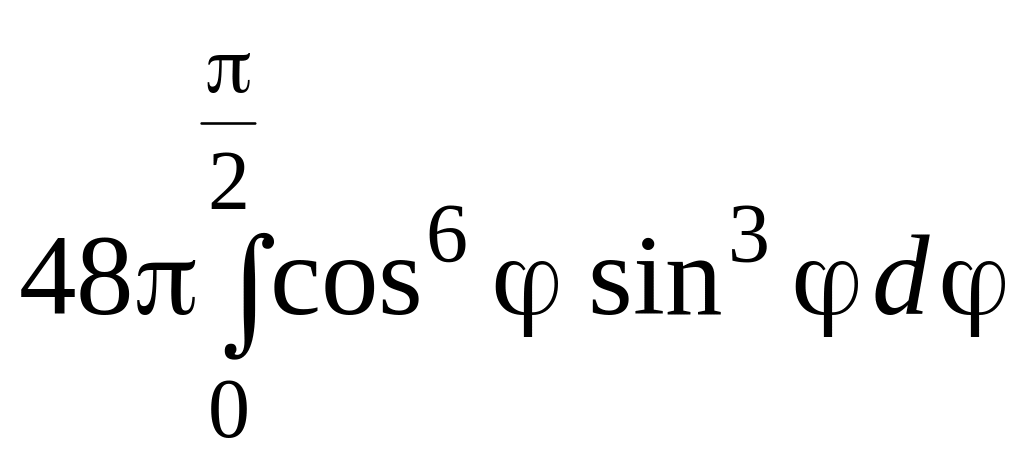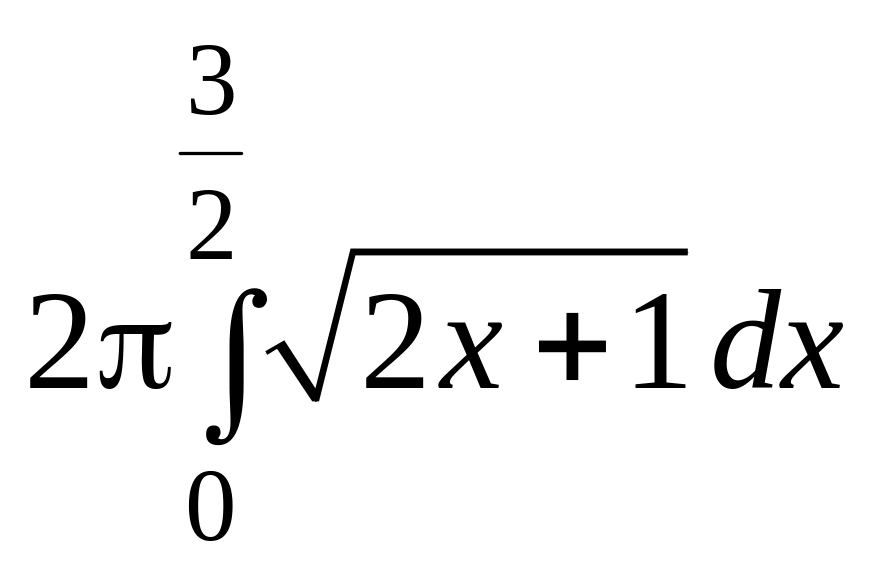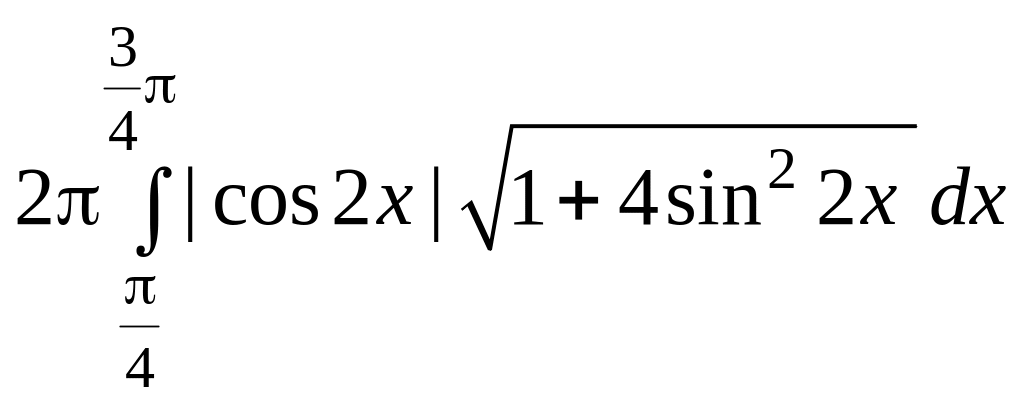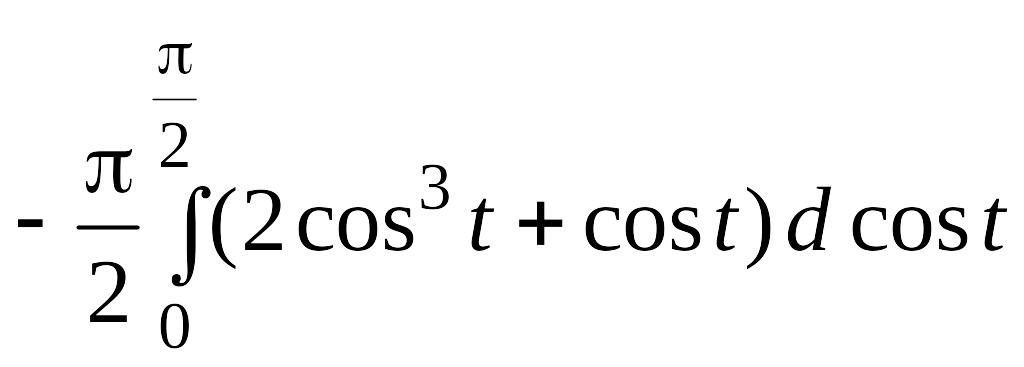Форумы
>
Консультация по матанализу
>
Найти длину петли линии
Поиск
| Автор | Сообщение |
|---|---|
|
alya reznichenko
# 2 июн 2014 |
Найти длину петли линии: |
|
o_a
# 2 июн 2014 |
Длина дуги кривой функции, заданной параметрически: |
Форумы
>
Консультация по матанализу
>
Найти длину петли линии
Чтобы написать сообщение, необходимо войти или зарегистрироваться
Тема: Длина дуги (Прочитано 1990 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Найти длину петли кривой:
( x = {t^2},y = t(frac{1}
{3} – {t^2})
)
Думаю по формуле:
( l = intlimits_{t1}^{t2} {sqrt {x{‘^2} + y{‘^2}} } dt )
Начал находить корень
( sqrt {{{(2t)}^2} + {{(frac{1}
{3} – 3{t^2})}^2}} = sqrt {4{t^2} + frac{1}
{9} – 2{t^2} + 9{t^4}} = sqrt {2{t^2} + 9{t^4} + frac{1}
{9}} … ) А как дальше упростить,а какие будут пределы интегрирования?
Под корнем у тебя полный квадрат! Вперёд!!!
Точно)а я не увидел)
получается
( 3{t^2} + 1/3 )
а какие пределы?
Двукратные корни у тебя при t=0 и при ( t=frac{1}{sqrt 3} )
А вообще прочитайте про кривые Жордана! и понятие кратных точек для них) и сразу станет где петля)
Математику нельзя изучать, наблюдая, как это делает кто-то другой!
Вычисление длины плоской кривой. Основные формулы
Если плоская кривая
задана как график функции y
= f(x),
a
≤ x
≤ b,
и производная y
= f
(x)
непрерывна, то длина дуги этой кривой
выражается интегралом
l
=
=
.
Если кривая задана
параметрически x
= x(t),
y
= y(t),
≤ t
≤
и производные x
(t)
и y
(t)
непрерывны на отрезке [,
],
то длина дуги кривой выражается интегралом
l
=
.
Если кривая задана
уравнением r
=
r(),
≤
≤ ,
в полярных координатах и r
()
непрерывна на отрезке [,
],
то длина l
дуги кривой выражается интегралом
l
=
.
Если
Г –
пространственная
кривая, заданная параметрически: x
= x(t),
y
= y(t),
z
= z(t),
≤ t
≤ ,
производные x
(t),
y
(t)
и z
(t)
непрерывны на отрезке [,
],
то длина Г
находится
по формуле
l
=
.
Замечание.
Пусть Г – некоторая кривая на плоскости
xOy.
Выражение
dl
=
,
где dx2
= (dx)2,
dy2
= (dy)2,
называется дифференциалом длины дуги.
Используя это понятие, можно единообразно
записать формулу для вычисления длины
кривой
l
=
=
,
где
и ,
≤ ,
обозначают границы изменения параметра,
с помощью которого задается кривая.
Пусть кривая Г есть график функции
x
= x(y),
c
≤ y
≤ d.
Тогда dx
=
x
(y)
dy
и мы получаем
l
=
=
.
Если кривая Г
задана параметрически, то dx
=
x
(t)
dt,
dy
=
y
(t)
dt
и мы получаем
l
=
=
=
.
Задание кривой с
помощью полярных координат r
= r(),
≤ ≤
,
есть частный случай параметрического
задания: x
= r()cos
,
y
=
= r()
sin
.
Параметром здесь является .
Вычисляя дифференциалы dx
= (r cos –
r sin )
d,
dy
= (r sin
+ r
cos ) d,
убеждаемся, что
dl
=
=
.
Для пространственной
кривой Г
дифференциалом
длины дуги называется выражение l
=
и длину кривой
Г
можно выразить
интегралом
l
=
=
,
где
и
(
≤ ) –
концы отрезка [,
] –
промежутка изменения параметра, с
помощью которого задается кривая.
Рассмотрим примеры.
Вычислить
длину дуги кривой.
5.19.
y
=
1 – ln cos
x,
0 ≤
x ≤
.
5.20.
y
=
2
,
0 ≤
x ≤
1.
5.21.
x
=
,
0 ≤
y ≤
4.
5.22.
3y2
=
x(x
– 1)2
(длину петли).
5.23.
y =
,
0 ≤
x ≤
ln 4.
5.24.
y
=
,
0 ≤ x
≤
.
Решение.
5.19. Так как y
=
=
tg
x,
то

.
5.20. Так как
,
то

.
Можно было
рассмотреть нашу кривую как график
функции
,
.
Тогда вычисление длины кривой свелось
бы к нахождению интеграла
.
5.21. Вычисляем
производную
=
и далее
=
=
,
откуда
=
=
=
.
5.22. Из условия
следует, что y
= 0 при x
= 0 и x
= 1, причем
линия симметрична относительно оси Ox,
так как y
входит в уравнение в четной степени.
Ясно, что достаточно вычислить длину
половины петли, задаваемой уравнением
y
=
,
.
(Вторая половина петли есть график
функции
).
Так как
,
=
,
то мы получаем
=
=
.
5.23.
Делаем предварительные вычисления:
=
–
=
.
Вычисляем длину
кривой
l
=
=
=
= 2.
5.24. Вычисляем
производную:
=
,
тогда
=
=
.
Вычисляем длину
кривой
l
=
=
=
=
=
=
=
=
=
.
Вычислить длину
кривой, заданной в полярных координатах.
5.25.
r
=
,
–
≤
≤
.
5.26.
r
= a(1
+ cos
),
0 ≤
≤ 2π
(кардиоида).
5.27.
r
= th
,
0 ≤
≤
2.
5.28.
r
= a cos4
.
Решение.
5.25. Вычисляем длину
кривой по формуле
l
=
=
=
=
=
=
=
.
5.26.
l
=
=
=
=
=
=
–
=
=
–
= 4a + 4a
= 8a.
5.27.
l
=
=
=
=
=
=
=
=
=
=
= 1 – th1.
5

Рис. 2.16
.28. Функция cos
имеет период 8π.
Функции
,
cos2
,
cos4
и т.п. имеют период 4π.
Поскольку
=
,
то линия симметрична относительно
полярной оси и при изменении
от 0 до 2π полярный радиус опишет половину
линии. Найдем длину половины кривой
(рис. 2.16) и затем удвоим результат.
Вычисляем
= a2
+
=
.
Отсюда следует
l
=
=
=
=
=
=
.
Вычислить длину
кривой, заданной параметрически.
5.29.
x
= 6t5,
y
= 5t(1
– t8),
0 ≤
t
≤ 1.
5.30.
x
= ln(1 +
t2),
y
= 2arctg t –
2t
+
8, 0 ≤
t
≤ 1.
5.31.
x
= t
–
sh
2t,
y
= 2 ch t,
0 ≤
t
≤ 1.
5.32.
x
= 2 cos3
t,
y
= 2 sin3
t.
5.33.
x
=
t2,
y
= t
– t3
(длину петли).
Решение.
5.29. Вычисляем,
используя соответствующую формулу:
l
=
=
=
= 5
= 5
=
= 10.
5.30.
=
+
=
.
Поэтому
l
=
=
=
.
5.31.
= (1 – ch 2t)2
+ 4sh2t
= |
ch 2t –
1 = 2 sh2
t |
= 4 sh4 t
+ 4sh2 t
=
= 4 sh2
t
ch2 t
= sh2
2t.
Поэтому
l
=
=
=
= sh2 1.
5.32.
Уравнение линии (астроиды) в декартовых
координатах имеет вид
или
(рис. 2.17).
О

Рис.
2.17
тсюда следует, что линия симметрична
относительно обеих осей координат.
Вычислим четверть длины астроиды, что
соответствует изменению параметра t
от 0 до
,
и результат учетверим. Вычисляем
= 36 cos4
t
sin2 t
+ 36 sin4 t
cos2 t
=
= 36 sin2
t
cos2 t
= 9 sin2 2t.
Отсюда следует
l
=
=
= 6 + 6 = 12.
5.33. Если выразить
y
через x,
то мы получаем
,
откуда следует,
что при x
[0,
]
графики симметричных относительно оси
Ox
функций
и
образуют замкнутый
контур на плоскости xOy
(петлю). График функции
получается, когда
t
изменяется от –1 до 0, а при изменении t
от 0 до 1 точка (x,
y)
движется по графику функции
от точки O
(0, 0) до точки A(
,
0).
Вычисляем сначала
= 12t2
+ (1 – 3t2)2
= (1 + 3t2)2.
Поэтому
l
=
=
= 4.
Вычислить длину
дуги пространственной кривой.
5.34.
x
= 3t
– t3,
y
= 3t2,
z
= 3t
+
t3,
0 ≤ t
≤ 1.
5.35.
x
= at,
y
=
,
z
=
,
≤
t
≤ 1.
5.36.
x
= et,
y
= e-t,
z
=
t,
0 ≤
t
≤ 2.
5.37.
x
= a
(1 + cos
t),
y
=
a(t
– sin
t),
z
= 4
a sin
,
0 ≤
t
≤ 2.
Решение.
5.34. Вычисляем длину
кривой по формуле
l
=
=
=
=
=
=
= 4
.
5.35.
=
=
=
=
=
.
Отсюда получаем
l
=
=
=
=
.
5.36. Имеем
=
e2t+
e–2t
+2
= (et
+
e–t)2.
Откуда
получаем
l
=
=
=
= 2 sh
2.
5.37.
Сделаем предварительные вычисления:
= 4
=
=
=
4a2.
Мы использовали
здесь тригонометрическую формулу 1 –
cos t
= =
.
Вычисляем длину
кривой
l
=
= 4a.
Вычисление
объемов и площадей поверхностей. Основные
формулы.
Пусть S(x) –
площадь сечения тела V
плоскостью, перпендикулярной к оси Ox
в точке с абсциссой x,
a
и b –
левая и правая границы изменения x.
Тогда объем тела V
выражается интегралом
V
=
.
Если тело V
образовано вращением вокруг оси Ox
криволинейной трапеции, ограниченной
кривой y
= f(x)
≥ 0, a
≤ x
≤ b,
осью абсцисс и прямыми x
= a,
x
= b,
то объем тела V
вычисляется по формуле
V
=
=
.
Если
тело образовано вращением вокруг оси
Oy
криволинейной трапеции, образованной
подграфиком функции x
= g(y),
c≤
y
≤ d
(g(y)
≥ 0), то
объем тела выражается интегралом
V
=
=
.
Если вокруг оси
Oy
вращается криволинейная трапеция,
ограниченная
графиком функции y
= f(x)
≥ 0, a
≤
x
≤
b,
осью абсцисс и прямыми x
=
a,
x
=
b,
то объем получившегося тела выражается
интегралом
V
=
=
.
Если кривая задана
параметрически или в полярных координатах,
то следует сделать соответствующую
замену переменных в указанных выше
формулах.
Площадь поверхности,
образованной вращением вокруг оси Ox
дуги Г кривой y
= f(x),
a
≤ x
≤ b,
где f(x)
имеет на отрезке [a,
b]
непрерывную производную
,
выражается интегралом
S
=
=
.
Поскольку
–
дифференциал длины дуги, то формулу
можно записать в виде
S
=
.
Пусть кривая задана
параметрически x
= x(t),
y
= y(t),
≤ t
≤ ,
где функции
x(t)
и y(t)
имеют на отрезке [,
]
непрерывные производные x(t)
и y(t).
Площадь S
поверхности,
образованной при вращении данной кривой
вокруг оси Ox
равна
S
=
=
.
Задание кривой с
помощью полярных координат r
= r(),
≤
≤ ,
есть частный случай параметрического
задания, так как в этом случае
x
= r()
cos ,
y =
r()
sin .
Рассмотрим примеры.
5.38.
На всех хордах круга радиуса R,
параллельных одному направлению,
построены симметричные параболические
сегменты постоянной высоты h
(рис. 2.18).
Плоскости сегментов перпендикулярны
к плоскости круга. Найти объем образованного
таким образом тела.

а б
Рис. 2.18
Решение.
Найдем вначале площадь параболического
сегмента с основанием a
и высотой h
(рис. 2.18, б).
Расположим оси координат так, что
основание сегмента будет находиться
на оси абсцисс и начало координат делит
это основание пополам. Уравнение параболы
имеет вид
.
Так как y(0)
= h,
то
= –
.
Тогда уравнение параболы принимает вид
.
Ищем площадь
сегмента
S
=
=
=
=
ah.
Расположим оси
координат так, как показано на рис. 2.18,
а.
Тогда длина половины хорды, пересекающей
ось абсцисс в точке x,
есть
.
Следовательно, площадь параболического
сегмента, соответствующего значению
x,
равна S(x)
=
.
Согласно формуле для объема, получаем
V
=
=
=
=
=
=
=
.
5.39. Найти объем
тела, ограниченного поверхностями z
= 4 – y2,
x
= 0, x
= a,
y
= 0, z
= 0.
Р
Рис. 2.19
ешение. Найдем площадь
сечения тела плоскостью, перпендикулярной
к оси Ox,
(0 ≤ x
≤ a)
(рис. 2.19). Нам необходимо знать площадь
половины параболического сегмента с a
= 2, h
= 4. Как мы знаем из решения предыдущей
задачи, эта площадь равна
S(x)
=
=
,
0 ≤ x
≤ a.
Отсюда получаем
V
=
=
=
.
Найти объем тела,
образованного вращением фигуры,
ограниченной следующими линиями.
5.40.
y
= sin
x,
x
= 0, 0 ≤ x
≤ π, вокруг оси: а)
Ox,
б)
Oy.
5.41.
y
= 2x,
y
=
,
x
= 0,
y
= 0,
вокруг
оси
Ox.
5.42.
y
= x(3
– x),
y
= x,
вокруг оси: а)
Ox,
б)
Oy.
5.43.
y
= cos
x,
y
= 1,
0
≤
x
≤ 2π,
вокруг
оси
Oy.
5.44.
y
= ex+6,
y
= e2x,
x
= 0, вокруг оси: а)
Ox,
б)
Oy.
5.45.
y
=
,
y
= 0, x
≥ 1, вокруг оси Ox.
5.46.
y
=
,
y
= 0, x
≥ 0, вокруг оси Ox.
5.47.
y
=
,
y
= 0, вокруг оси Oy,
.
5.48.
x
= 4t2,
y
=
(петля), вокруг оси Ox.
5.49.
x
= a
ch3
t,
y
=
a
sh3
t,
x
=
2
a,
вокруг
оси
Ox.
5.50.
r
= 2cos2
,
вокруг полярной оси.
5.51.
r
=
,
0 ≤
≤
,
вокруг полярной оси.
Решение.
5.40. Вычислим объем
полученный вращением вокруг оси Ox.
Имеем
V
=
=
=
.
Теперь вычислим
объем тела, получаемого при вращении
фигуры вокруг оси Oy:
V
=
=
=
=
=
.
5.41. Абсцисса точки
пересечения графиков (рис. 2.20) равна 1.
Искомый объем выражается суммой двух
интегралов:
V
=
+
=
+
.
В

Рис. 2.20
ычислим интегралы с логарифмом
отдельно, применяя формулу интегрирования
по частям. Имеем
=
=
=
.
=
=
=
–
=
=
–
+
+ С.
Отсюда получаем,
V
=
+ 12π –
+
=

Рис. 2.21
= –
+
– 4π.
5.42. Несложно
находится абсцисса точки пересечения
графиков x
= 2 (рис. 2.21). Вычисляем объем, получаемый
при вращении фигуры вокруг
оси Ox:
V
=
=
=
=
=
=
.
При вычислении
объема, получающегося при вращении
вокруг оси Oy,
воспользуемся следующей формулой:
V
=
–
,
где y1
= 3x
– x2,
y2
=
x.
Тогда
V
=
–
=
=
.
5.43. Рассмотрим два
способа вычисления искомого объема.

а б
Рис. 2.22
Решение уравнения
cos
x
= y
при 0≤ x
≤ π относительно x
есть
x
= arccos
y,
решением уравнения cos
x
= y
при π ≤ x
≤ 2π является
x
=2π – arccos
y.
Тогда объем можно вычислить следующим
образом (рис. 2.22, б):
V
=
=
=
=
= 4π3.
Но можно, используя
другую формулу, вычислять объем и так
(рис. 2.22, а),
где
:
V
= 8π3 –
= 8π3 –
=
= 8π3 – 4π3
= 4π3,
где слагаемое 8π3
есть объем цилиндра, у которого в
основании – круг радиуса 2π и высота
равна 2.
5

Рис. 2.23
.44. Абсцисса точка пересечения
графиков равна ln
3 (рис. 2.23).
Вычисляем вначале
объем тела, получаемого при вращении
фигуры вокруг оси Ox.
V
=
=
=
= (8 + 36 ln 3) .
Для вычисления
объема тела, получаемого вращением
фигуры вокруг оси Oy,
мы, чтобы не искать обратные функции,
воспользуемся следующей формулой:
V
=
–
,
где
y1
=
ex
+
6,
y2
=
e2x.
Тогда
V
=
+
–
= 6π ln2
3 +
–
=
= 6π ln2
3 +
=
= 3π
ln 3(ln 9 – 1).
5.45. Объем тела
выражается несобственным интегралом
V
=
=
=
.
5.46. Вычисляем объем
V
=
=
=
=
=
=
.
5.47. Объем можно
вычислить двумя способами.
Найдя обратную
функцию (x
≥ 0), из
уравнения y
=
,
x
=
,
приходим к интегралу
V
=
.
Можно использовать
формулу
V
=
=
=
=
= π.
Мы видим, что в
этом примере второй способ вычисления
предпочтительнее.
5.48. Петля симметрична
относительно оси Ox,
верхняя часть петли есть график функции
y
=
,
0 ≤ x ≤ 12,
и соответствует
изменению параметра t
от 0 до
.
Вычисляем объем
V
=
=
=
=
= 48π.
5.49. В
декартовых координатах уравнение линии
выглядит так:
=
.
Отсюда заключаем, что линия симметрична
относительно оси Ox,
ясно так же, что a≤
x
≤
a.
Верхняя ветвь (y
≥ 0)
соответствует изменению параметра t
от 0 до
(решения уравнений
).
Вычисляем объем тела, полученного
вращением вокруг оси Ox
верхней ветви кривой (y
≥ 0),
V
=
=

=
5.50.
Линия представляет собой два симметричных
относительно оси Oy
лепестка, симметричных, в свою очередь,
относительно оси Ox
(рис. 2.24).
Первый соответствует изменению параметра
от –
до
,
второй – от
до π и
от –π до –
.
Вычислим объем тела, получаемого
вращением половины лепестка, и удвоим
результат:
V
=
=

Рис. 2.24
=
=
=
=
=
=
=
=
=
=
.
Минус
перед первым интегралом поставлен
потому, что x
= r
cos
= = 2
cos3
при изменении
от 0 до
убывает. Действительно,
V
=
=
=
=
=
.
5.51.
Вычисляем объем
при
:
V
=
=
=
=
=
=
=
=
=
.
Найти площадь
поверхности, образованной при вращении
дуги кривой.
5.52.
y2
= 2x,
2x
= 3, вокруг
оси Ox.
5.53.
y
= 3 c
h
,
–1
≤ x
≤ 1, вокруг
оси Ox.
5.54.
y
= cos
2x,
≤ x
≤
,
вокруг оси Ox.
5.55.
,
вокруг оси Oy.
5.56.
x
=
,
y
=
,
0 ≤
t
≤
π,
вокруг
оси
Ox.
5.57.
x
=
2cos
t
– cos2
t,
y
= 2sin
t
– sin2
t,
0 ≤ t
≤
π,
вокруг
оси
Ox.
5.58.
y
=
(arcsin
x
+
),
0 ≤
x ≤
1, вокруг
оси
Oy.
5.59.
r
=
,
вокруг полярной оси.
Решение.
5.52. Достаточно
рассмотреть поверхность, образованную
вращением кривой y
=
,
0 ≤ x
≤ 3/2, вокруг
оси Ox.
Имеем
S
=
=
=
=
=
=
.
5.53.
S
=
=
=
=
=
=
+6
.
5

Рис. 2.25
.54.
S
=
=
=
=
=
=
=
=
.
5.55. Используем
формулу
S
=
.
Имеем


Используя результаты
задачи 3.6 из гл. 1, § 3, получаем
5.56.
y
=
при изменении t
от 0 до
,
при этом x
возрастает от 0 до
.
Когда t
возрастает от
до π,
переменная x
убывает от
до 0, при этом
y
=
.
Таким образом,
наша линия – петля, симметричная
относительно оси Ox.
Поэтому
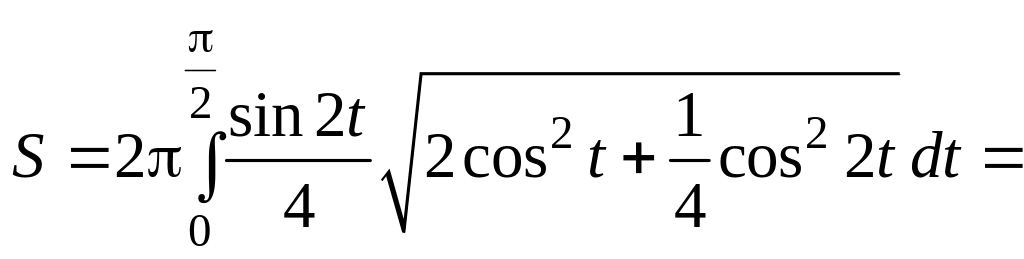
=
=
=
=
=
=
.
5.57. Вычислим
предварительно дифференциал длины дуги
dl
= =
.
dl
=
=
=
=
4|sin
|dt
= 4 sin
dt,
так как
.
Вычисляем площадь поверхности вращения
5.58. Выражать в
данном случае x
через y
было бы крайне затруднительно. Поэтому
параметризуем кривую, взяв за параметр
x
= t.
Тогда
S
=
=
=
=
=
=
=
,
так как
=
=
.
5.59. Линия представляет
собой два лепестка, симметричные
относительно обеих осей координат Ox
и Oy
(x
= r
cos
= 3 cos
,
y
= r
sin
= 3 sin
).
Достаточно рассмотреть дугу кривой,
соответствующую изменению
от 0 до
и затем удвоить результат. Вычисляем
площадь поверхности вращения
S
=
=
=
=
=
.
|
0 / 0 / 0 Регистрация: 11.03.2010 Сообщений: 18 |
|
|
1 |
|
Длина петли кривой12.04.2010, 13:27. Показов 13473. Ответов 1
Вычислить длину петли кривой
0 |
|
3132 / 1325 / 156 Регистрация: 19.12.2009 Сообщений: 1,808 |
|
|
12.04.2010, 16:57 |
2 |
|
Глафира, для этого есть примитивные формулы. Миниатюры
2 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
12.04.2010, 16:57 |
|
Помогаю со студенческими работами здесь Длина петли линии длина кривой длина дуги кривой Длина дуги кривой Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 2 |
$$
One,,,loop:,,y = pm frac{{xsqrt {2a^2 – x^2 } }}{{4a}},,,,,0 le x le sqrt 2 a,,,({rm{assuming}},a > 0).$$
$$
begin{array}{l}
L = 2intlimits_0^{sqrt 2 a} {sqrt {1 + y’^2 } dx = } 2intlimits_0^{sqrt 2 a} {frac{{|x^2 – 3a^2 |}}{{2asqrt {2a^2 – x^2 } }}dx = } frac{1}{a}intlimits_0^{sqrt 2 a} {frac{{2a^2 – x^2 + a^2 }}{{sqrt {2a^2 – x^2 } }}dx = } \
= frac{1}{a}left( {intlimits_0^{sqrt 2 a} {frac{{2a^2 – x^2 }}{{sqrt {2a^2 – x^2 } }}} dx + intlimits_0^{sqrt 2 a} {frac{{a^2 }}{{sqrt {2a^2 – x^2 } }}} dx} right) = left{ {x = sqrt 2 asin t} right} = \
end{array}$$
$$
= frac{1}{a}left( {intlimits_0^{frac{pi }{2}} {2a^2 cos ^2 tdt + intlimits_0^{frac{pi }{2}} {a^2 dt} } } right) = frac{1}{a}left( {frac{{pi a^2 }}{2} + frac{{pi a^2 }}{2}} right) = pi a.$$
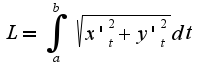 В данном примере
В данном примере 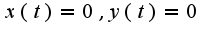 при
при 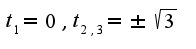 Поэтому
Поэтому