Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат (x, y, z) и времени t.
 . . |
(5.2.1) |
Эта функция должна быть периодической как относительно времени, так и координат (волна – это распространяющееся колебание, следовательно периодически повторяющееся движение). Кроме того, точки, отстоящие друг от друга на расстоянии l, колеблются одинаковым образом.
Уравнение плоской волны
Найдем вид функции x в случае плоской волны, предполагая, что колебания носят гармонический характер.
Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x. Так как все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от х и t: 


Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время 
Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости 
 , , |
(5.2.3) |
– это уравнение плоской волны.
Таким образом, x есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания 
Такой же вид уравнение (5.2.3) будет иметь, если колебания распространяются вдоль оси y или z.
В общем виде уравнение плоской волны записывается так:
Выражения (5.2.3) и (5.2.4) есть уравнения бегущей волны.
Уравнение (5.2.3) описывает волну, распространяющуюся в сторону увеличения x. Волна, распространяющаяся в противоположном направлении, имеет вид:

Уравнение волны можно записать и в другом виде.
Введем волновое число 
 , , |
(5.2.5) |
где 

Так как 


 . . |
(5.2.6) |
Уравнение сферической волны
В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической.
Предположим, что фаза колебаний источника равна wt (т.е. 


где А равна амплитуде на расстоянии от источника равном единице.
Уравнение (5.2.7) неприменимо для малых r, т.к. при 

Уравнение плоской и сферической волн. Длина волны, волновое число, фазовая скорость
Уравнением волны называется выражение, которое определяет смещение 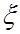
Найдем явный вид функции x для плоской волны, считая что колебания носят гармонический характер. Направим ось х вдоль направления распространения волны, тогда волновые поверхности будут перпендикулярны к оси х. Так как все точки, принадлежащие волновой поверхности, колеблются одинаково, то смещение x будет зависеть только от х и t:
Пусть колебания точек, лежащих в плоскости х = 0
(рис. 2.2.1), описываются гармонической функцией:
Частицы среды расположенные слева и справа от источника будут совершать гармонические колебания, смещения которых в некоторый момент времени t можно представить графиком (рис.2.2.2).
Кратчайшее расстояние между частицами, колеблющимися одинаковым образом (в одинаковой фазе), называется длиной волны l. Длина волны, очевидно, равна расстоянию, на которое распространяется волна за период колебаний частиц:
Учитывая связь периода колебаний T с частотой n, получим, что
Найдем уравнение колебаний частиц в плоскости, соответствующей произвольному значению x (это и будет уравнение плоской волны).
Для того чтобы пройти путь от плоскости x = 0 до плоскости, соответствующей значению x, волна затратит время
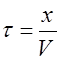
где V — скорость распространения волны.
Следовательно, колебания частиц в плоскости x будет отставать по времени на t от колебаний частиц в плоскости x=0, то есть уравнение колебаний будет иметь вид:
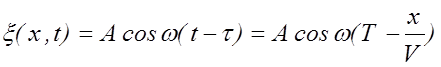
Таким образом, уравнение плоской волны имеет вид:
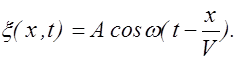
При получении уравнения (2.2.7) изменение амплитуды колебаний не учитывалось, то есть это уравнение справедливо, если энергия волны не поглощается средой.
Найдем скорость распространения волны. Для этого зафиксируем значение фазы в уравнении (2.2.7), то есть положим:
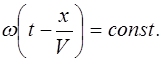
Это выражение определяет координату x, для которой зафиксированное значение фазы достигается в данный момент времени t. Определив из (2.2.8) значение 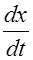
dt- 
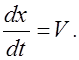
Из (2.2.9) следует, что фазовая скорость волны (2.2.7) положительна. Таким образом, уравнение (2.2.7) описывает волну, распространяющуюся в положительном направлении оси X.Очевидно, уравнение волны, распространяющейся в противоположном направлении, можно получить, заменив в уравнении (2.2.7) X на -X, то есть
x=A×cosw(t+ 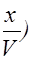
Действительно, приравняв константе фазу волны (2.2.10) и продифференцировав, получим 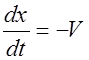
Уравнению плоской волны можно придать симметричный относительно t и x вид. Для этого введем волновое число k:
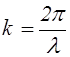
С учетом формулы (2.2.4) из (2.2.11) получаем соотношение
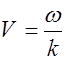
где 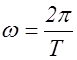
Заменив в уравнении (2.2.7) V согласно (2.2.12) и внеся в скобки w, получим уравнение плоской волны в виде
Очевидно, уравнение (2.2.10) также может быть записано в симметричном относительно t и x виде и будет отличаться от (2.2.13) знаком в аргументе у косинуса.
Получим теперь уравнение сферической волны. Если рассматривать волну на расстояниях от источника, значительно превышающих его размеры, то источник можно считать точечным. Такой источник в случае, когда скорость распространения волны во всех направлениях одна и та же, создает сферические волны. Пусть фаза колебаний источника равна wt , тогда фаза колебаний частиц среды лежащих на волновой поверхности радиуса r будет равна 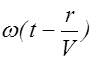
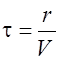
Как будет показано в §2.4,амплитуда колебаний в сферической волне убывает по закону 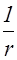
x= 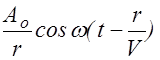
где константа A0 — численно равна амплитуде колебаний на расстоянии, равном единице длины. Размерность ее равна размерности амплитуды (зависит от физической природы волнового процесса), умноженной на размерность длины.
Получим уравнение плоской волны, распространяющейся в произвольном направлении, образующем с осями координат x, y, 
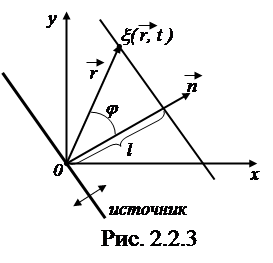
x(0,t) = Acoswt. (2.2.15)
В плоскости, отстоящей от начала координат на расстоянии l, колебания частиц будут отставать от колебаний источника на время t 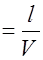

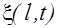
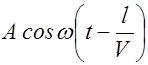
Выразим l через радиус-вектор 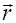
Для этого введем единичный вектор 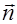
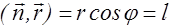
Подставим выражение (2.2.17) в уравнение (2.2.16), тогда получим
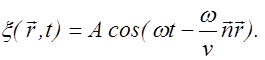
Учтем, что 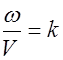
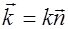
Как найти длину волны из уравнения плоской волны
отстоящие друг от друга на расстоянии λ, колеблются одинаковым образом.
Уравнение плоской волны
Найдем вид функции . в случае плоской волны, предполагая, что колебания носят гармонический характер.
Пусть колебание точек, лежащих в плоскости x = 0, имеет вид (при начальной фазе ф = 0)
Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время τ = х/v. Следовательно, колебания частиц в плоскости x будут отставать по времени на τ от колебаний частиц в плоскости x = 0, т. е.
— это уравнение плоской волны (рис. 2.4.3). Таким образом, . есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания A = const. Это будет, если энергия волны не поглощается средой.
Такой же вид уравнение (2.4.5) будет иметь, если колебания распространяются вдоль оси y или z.
В общем виде уравнение плоской волны записывается так:
Выражения (2.4.5) и (2.4.6) есть уравнения бегущей волны. Уравнение волны можно записать и в другом виде.
Введем волновое число k = 2π/λ, или в векторной форме
где k — волновой вектор; n — нормаль к волновой поверхности.
Так как λ = vT , то k = 2π/vT = 2πν/v = ω/v. Отсюда v = ω/k.
Тогда уравнение плоской волны запишется так:
источники:
http://helpiks.org/4-19742.html
http://www.chem-astu.ru/chair/study/physics-part1/?p=136
Уравнение плоской волны. Фазовая скорость
Волновой
поверхностью
называют геометрическое место точек,
колеблющихся в одинаковой фазе.
В
простейших случаях они имеет форму
плоскости или сферы, а соответствующая
волна называется плоской или сферической.
Фронтом
волны
называется геометрическое место точек,
до которых в данный момент времени
доходят колебания. Фронт волны разделяет
области пространства уже вовлеченную
в волновой процесс и еще не вовлеченную.
Волновых поверхностей существует
бесконечное множество и они неподвижны,
а фронт волны один и он перемещается с
течением времени.
Рассмотрим
плоскую волну, распространяющуюся вдоль
оси х. Пусть частицы среды, лежащие в
плоскости x
= 0, перпендикулярной направлению
распространения волны, начинают в момент
t=0
совершать колебания по гармоническому
закону относительно исходного положения
равновесия. Это значит, что смещение
частиц от их положения равновесия ξ
изменяется во времени по закону синуса
или косинуса, например:
, (1)
где ξ
– смещение
данных частиц от их исходного положения
равновесия в момент времени t,
А
-максимальное значение смещения
(амплитуда); ω – циклическая частота.
Пренебрегая
затуханием в среде, получим уравнение
колебания частиц, в плоскости,
перпендикулярной направлению
распространения волны, соответствующей
произвольному значению x>0.
Пусть волна распространяется в направлении
возрастания координатых. Чтобы
пройти путь от плоскостиx=0
до указанной плоскостиx,
волне требуется время
(2)
где υ -скорость
перемещения постоянной фазы (фазовая
скорость).
Поэтому колебания
частиц, лежащих в плоскости х,
начнутся в моментt=τи будут происходить по такому же
закону, что и в плоскости х=0, но с
отставанием по времени на величинуτ,
а именно:
(3)
С учетом (2), выражение
(3) преобразуется:
(4)
Уравнение (4)
представляет собой уравнение плоской
бегущей волны, распространяющейся вдоль
положительного направления оси х.
Из него можно определить отклонение
частиц среды от равновесия в любой точке
пространства с координатой х
и в любой момент времени t
при распространении указанной волны.
Аргумент косинуса или синуса называют
фазой
колебания.
Фаза определяет состояние колебательного
процесса в данный момент времени (знак
и абсолютную величину относительного
отклонения частиц от их положения
равновесия).
Если плоская волна
распространяется в направлении убывания
х
(налево), то уравнение (4) преобразуется
к виду:
(5)
Расстояние
,
на которое волна распространяется за
период колебаний Т,
называется длиной
волны.
Учитывая,
что
(6)
где k
– волновое число. Уравнение волны (4)
можно записать в виде:
(7)
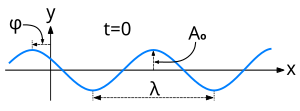
Можно также
определить длину
волны и как
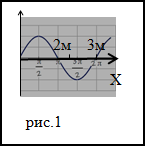
расстояние между двумя ближайшими
точками, фазы колебаний которых отличаются
на 2π (рис.1).
Как отмечено выше,
упругие волны в газах представляют
собой чередующиеся области с более
высоким и более низким давлением и
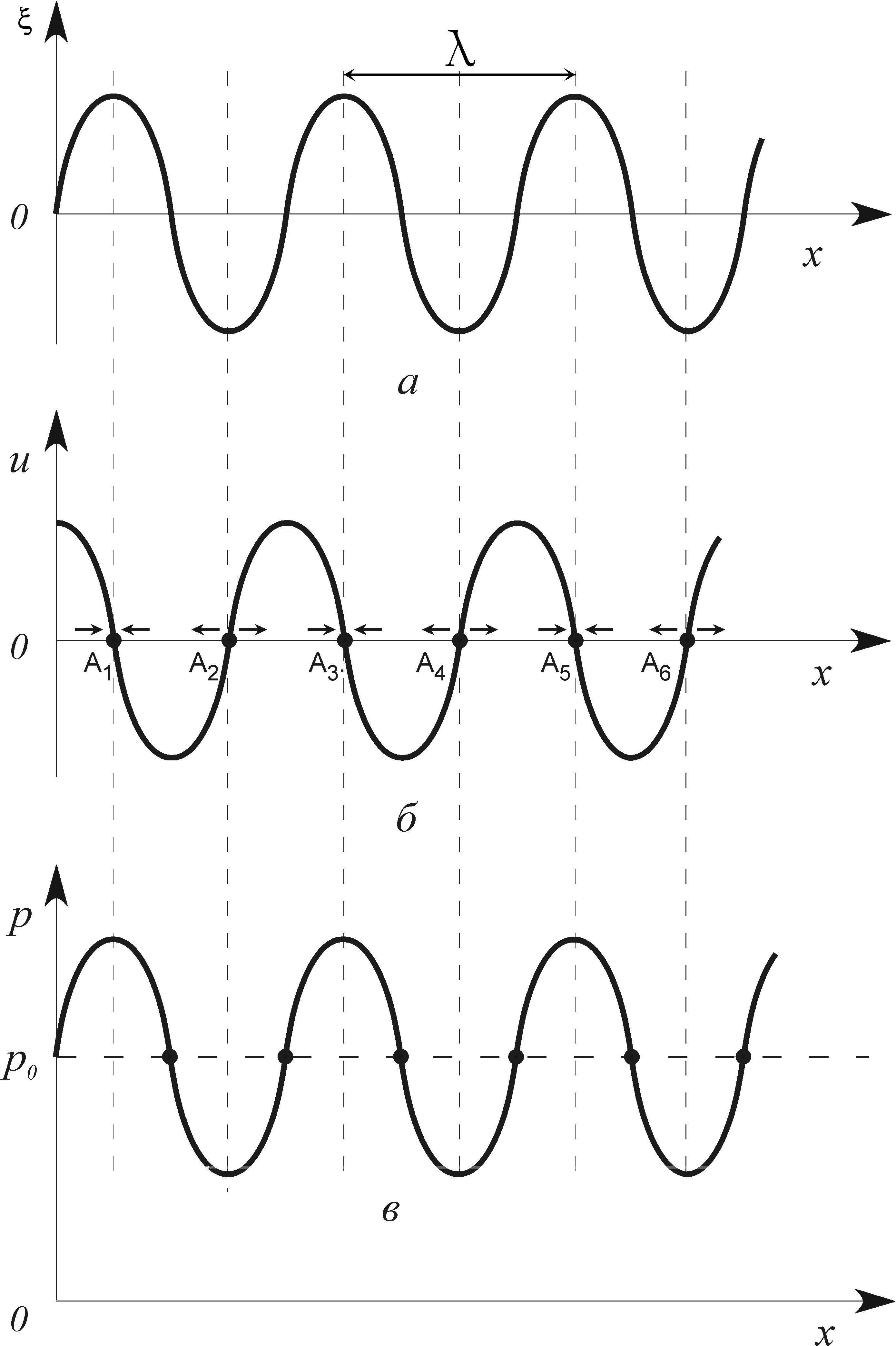
плотностью. Это иллюстрируется рис 1,
на котором представлены для некоторого
момента времени смещение частиц (а),
скорости их колебаний (б), давление или
плотность (в) в различных точках
пространства. Частицы среды колеблются
со скоростью
(не путать с фазовой скоростью υ). Слева
и справа от точекA1,
A3,
A5
и др. скорости частиц направлены к этим
точкам. Поэтому в данных точках образуются
максимумы плотности (давления). Справа
и слева от точек A2,
A4,
A6
и др. скорости частиц направлены от
данных точек и в них образуются минимумы
плотности (давления).
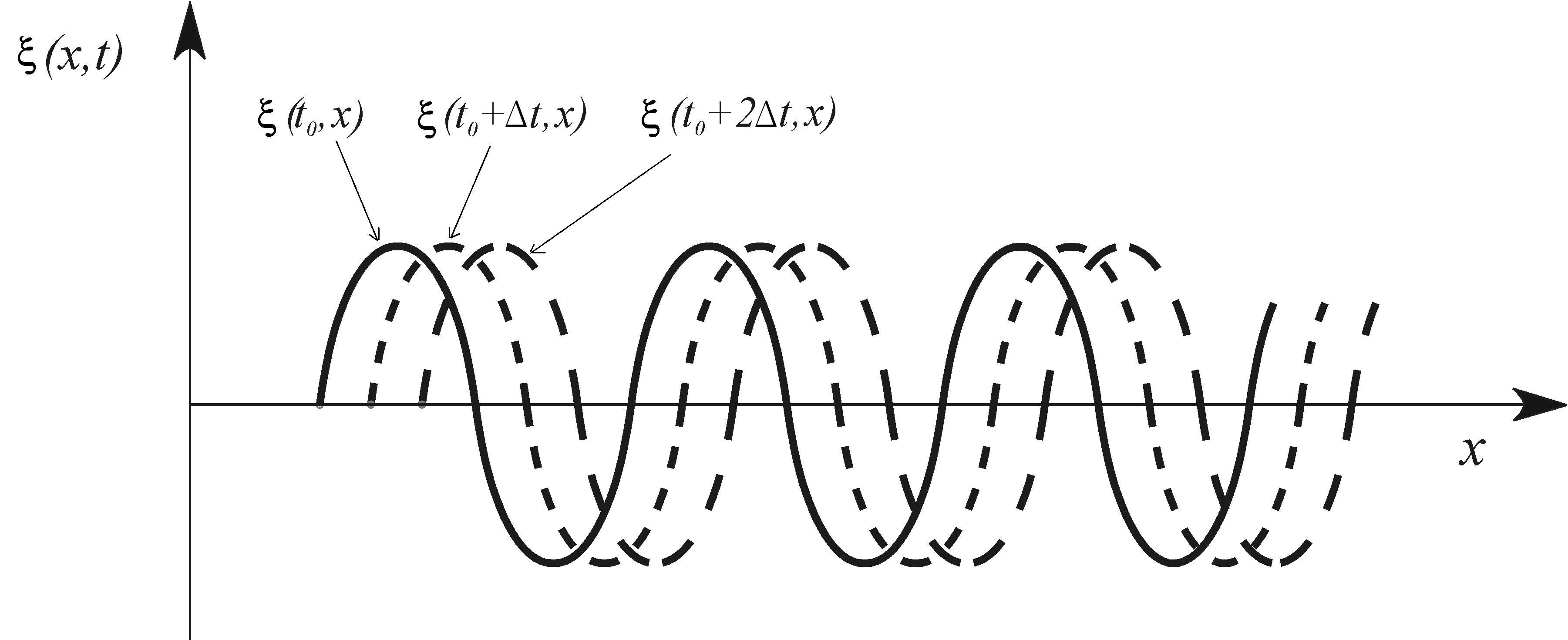
Смещение частиц
среды при распространении в ней бегущей
волны в различные моменты времени
представлены на рис. 2. Как видно, имеется
аналогия с волнами на поверхности
жидкости. Максимумы и минимумы отклонений
от положения равновесия перемещаются
в пространстве с течением времени с
фазовой скоростью υ. С такой же скоростью
перемещаются максимумы и минимумы
плотности (давления).
Фазовая скорость
волны зависит от упругих свойств и
плотности среды. Формулы для фазовых
скоростей продольной и поперечных волн
выведены в Приложении I.
Скорость
распространения
продольной волны:
(8)
Скорость
распространения поперечной волны
(9)
где E
– модуль растяжения и сжатия(модуль
Юнга), G
– модуль сдвига, ρ – плотность среды.
Рис. 1
Рис.
2
Звуковые волны в
воздухе являются продольными. Для
жидкостей и газов вместо модуля Юнга
в формулу (8) входит объемный модуль
упругости, который равен отношению
отклонения давления ΔΡ
к относительному изменению объема

Знак минус означает,
что увеличению давления (процессу сжатия
среды) соответствует уменьшение объема
и наоборот. Полагая
изменения
объема и давления бесконечно малыми,
можно записать
(11)
При распространении
волн в газах периодическое изменение
давления и плотности приводит к изменению
температуры различных участков среды,
так как сжатие и разрежение происходят
быстро, то смежные участки не успевают
обменяться энергией. Такие процессы,
происходящие без теплообмена с окружающей
средой, называются адиабатическими.
При адиабатическом процессе изменение
состояния газа описывается уравнением
Пуассона
(12)
Параметр
γ называют показателем адиабаты. Он
равен отношению молярных теплоемкостей
газа при постоянном давлении Cp
и постоянном объеме Cv
:
.
Взяв дифференциал
от обеих частей равенства (12), получаем
,
откуда
следует:
. (13)
Подставив (13) в
(11), получим для модуля упругости газа
. (14)
Подставив (14) в
(8), найдем скорость упругих волн в газах:
(15)
Из уравнения
Менделеева-Клапейрона
можно выразить плотность газа
, (16)
где
–
молярная масса.
Подставляя (16) в
(15), получим конечную формулу для
нахождения скорости звука в газе:
, (17)
где R
– универсальная газовая постоянная, Т
– температура газа.
Измерение скорости
звука – один из наиболее точных методов
определения показателя адиабаты.
Преобразуя формулу
(17),
получим:
(18)
Таким
образом, для определения показателя
адиабаты достаточно измерить температуру
газа и скорость распространения звука.
В
дальнейшем более удобно использовать
в уравнении волны косинус. Учитывая
(7),
уравнение бегущей волны можно представить
в виде:
(19)
где
–
волновое число.
Для
бегущей волны, распространяющейся
против положительного направления оси
х, получим:
(20)
Соседние файлы в папке физика лабы
- #
- #
- #
- #
- #
- #
- #
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 10 сентября 2020 года; проверки требуют 4 правки.
Пло́ская волна́ — волна, поверхность постоянной фазы которой представляет собой плоскость.
Фронт плоской волны неограничен по размерам, вектор фазовой скорости перпендикулярен фронту.
Плоская волна является частным решением волнового уравнения и удобной теоретической моделью: такая волна в природе не существует, так как плоский фронт волны начинается в 

Квазиплоская волна — волна, фронт которой близок к плоскому в некоторой ограниченной области. Если размеры области достаточно велики для характерного размера явления, то квазиплоскую волну можно приближённо считать плоской. Волну со сложным фронтом можно аппроксимировать суммой локальных квазиплоских волн, векторы фазовых скоростей которых нормальны реальному фронту в каждой его точке. Примерами источников квазиплоских электромагнитных волн являются лазер, зеркальная и линзовая антенны: распределение фазы электромагнитного поля в плоскости, параллельной апертуре (излучающему отверстию), близко к равномерному. По мере удаления от апертуры фронт волны принимает сложную форму.
Определение[править | править код]
Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Волновое уравнение для функции 
- где
— оператор Лапласа;
— искомая функция;
— радиус-вектор искомой точки;
— скорость волны;
— время.
Одномерный случай[править | править код]
Анимация движения плоской волны
В одномерном случае волновое уравнение принимает вид:
- где
— координата.
Частное решение этого уравнения для плоской гармонической волны:
- где
— величина возмущения в данной точке пространства
и в момент времени
;
— амплитуда волны;
— волновое число;
— круговая частота;
— начальная фаза колебаний.
Волновое число выражается:
- где
— пространственный период изменения функции длина волны.
Круговая частота колебания выражается:
- где
— период колебаний;
— частота колебания.
При подстановке в выражение для волны этих выражений волну можно описать также выражениями:
или:
или:
- где
— фазовая скорость распространения волны.
Многомерный случай[править | править код]
В общем случае уравнения плоской волны записывается в виде:
- где
— волновой вектор, равный
— волновое число;
— единичный вектор нормали, проведённый к волновому фронту;
— радиус-вектор точки,
— скалярное произведение векторов
и
.
Комплексная форма записи[править | править код]
Приведённые выше уравнения можно записать в так называемом комплексном виде:
или в многомерном случае:
Правильность этой формулы следует из формулы Эйлера для экспоненты с комплексным показателем.
Вообще говоря, функция 
Из комплексной записи гармонической функции также следует понятие комплексной амплитуды, равной 
Тогда 
Модуль комплексной функции даёт амплитуду колебаний, а аргумент — начальную фазу 
Экспоненциальная форма записи в некоторых случаях часто бывает удобнее тригонометрической.
Скорость волны[править | править код]
Энергия упругой плоской волны[править | править код]
Пусть дано, что 
Выделим в пространстве некий малый объём 


Тогда рассматриваемый объём обладает кинетической энергией:
и потенциальной энергией упругой деформации:
Полная энергия:
Плотность энергии, соответственно, равна:
Поляризация[править | править код]
Литература[править | править код]
- Савельев И. В. [Часть 2. Волны. Упругие волны.] // Курс общей физики / Под редакцией Гладнева Л. И., Михалина Н. А., Миртова Д. А.. — 3-е изд. — М.: Наука, 1988. — Т. 2. — С. 274—315. — 496 с. — 220 000 экз.
Примечания[править | править код]
См. также[править | править код]
- Сферическая волна
- Цилиндрическая волна
- Длина волны
Содержание:
- Определение и формула длины волны
- Длина стоячей волны
- Длина бегущей волны
- Длина бегущей волны
- Длина электромагнитной волны
- Единицы измерения длины волны
- Примеры решения задач
Определение и формула длины волны
Определение
Длиной волны называют кратчайшее пространственное расстояние между ее точками, совершающими колебания в одной фазе.
Обозначают длину волны, чаще всего буквой $lambda$ .
Для синусоидальных волн $lambda$ – это расстояние, на которое волна распространяется за один период
(T). Длину волны в этом случае еще называют пространственным периодом. Тогда формулой длины волны можно считать выражение:
$$lambda=v T=frac{v}{nu}=frac{2 pi}{k}$$
где v – скорость распространения волны, $nu=frac{1}{T}$ – частота колебаний,
$k=frac{omega}{v}$ – волновое число,
$T=frac{2 pi}{omega}$ – период волны,
$omega$ – циклическая частота волны.
Длина стоячей волны
Длиной стоячей волны($lambda_{st}$) называют расстояние в пространстве между
двумя пучностями (или узлами):
$$lambda_{s t}=frac{pi}{k}=frac{lambda}{2}(2)$$
где $lambda$ – длина бегущей волны. Надо заметить, что расстояние между соседними пучностью и
узлом связывает равенство:
$$frac{lambda_{s t}}{2}=frac{lambda}{4}(3)$$
Длина бегущей волны
В бегущей волне длина волны связана с фазовой скоростью (vph) формулой:
$$lambda=frac{v_{p h}}{nu}(4)$$
Длина бегущей волны
Разность фаз и длина волны
Две точки волны находящиеся на расстоянии
$Delta x$ имеют при колебании разность
фаз ($Delta varphi$), которая равна:
$$Delta varphi=frac{2 pi Delta x}{lambda}(5)$$
Длина электромагнитной волны
Скорость распространения электромагнитных волн в вакууме равна скорости света в вакууме
($c approx 3 cdot 10^{8}$ м/с), следовательно, длина электромагнитной волны в
вакууме, может быть рассчитана при помощи формулы:
$$lambda=c T=frac{c}{nu}(6)$$
Длина электромагнитной волны в веществе равна:
$$lambda=frac{c}{n nu}(7)$$
где $n=sqrt{varepsilon mu}$ – показатель преломления вещества,
$varepsilon$ – диэлектрическая проницаемость вещества,
$mu$ – магнитная проницаемость вещества.
Отметим, что все рассматриваемые формулы относят к случаю T=const.
Единицы измерения длины волны
Основной единицей измерения длины волны в системе СИ является: [$lambda$]=м
В СГС: [$lambda$]=см
Примеры решения задач
Пример
Задание. Каково приращение длины электромагнитной волны, имеющей частоту v=1 МГц при ее переходе в немагнитную среду,
которая имеет диэлектрическую проницаемость $varepsilon$=2?
Решение. Так как речь в условии задачи идет о немагнитной среде, в которую переходит волна, то считаем магнитную
проницаемость вещества равной единице ($mu$=1).
Длина рассматриваемой нами волны в вакууме равна:
$$lambda_{1}=frac{c}{nu}(1.1)$$
Длина волны в веществе:
$$lambda_{2}=frac{c}{n nu}=frac{c}{sqrt{varepsilon mu} cdot nu}(1.2)$$
Используя выражения (1.1) и (1.2) найдем изменение длины волны:
$$Delta lambda=lambda_{2}-lambda_{1}=frac{c}{sqrt{varepsilon mu} cdot nu}-frac{c}{nu}=frac{c}{nu}left(frac{1}{sqrt{varepsilon mu}}-1right)$$
Проведем вычисления, если нам известно помимо данных приведенных в условии задачи, что
$c approx 3 cdot 10^{8}$ м/с- скорость света в вакууме, и v=1 МГц=106 Гц:
$$Delta lambda=frac{3 cdot 10^{8}}{10^{6}}left(frac{1}{sqrt{4 cdot 1}}-1right)=-1,5 cdot 10^{2}(mathrm{~m})$$
Ответ. Длина волны уменьшится на 150 м

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Какова длина плоской синусоидальной волны, которая распространяется по оси X. Две точки, которые
находятся на оси X расположенные на расстояниях 2 м и 3 м от источника совершают колебания с разностью фаз равной
$Delta varphi=frac{3 pi}{5}$ . Каким будет период колебаний в волне, если ее скорость в данной среде равна v=2м/с?
Решение. Сделаем рисунок.
Основой для решения задачи будет формула:
$$Delta varphi=frac{2 pi Delta x}{lambda}=frac{2 pileft(x_{2}-x_{1}right)}{lambda}(2.1)$$
Выразим из (2.1) искомую длину волны, получим:
$$lambda=frac{2 pileft(x_{2}-x_{1}right)}{Delta varphi}(2.2)$$
Период колебаний связан с длиной волны формулой:
$$T=frac{lambda}{v}(2.3)$$
C учетом (2.2), имеем:
$$T=frac{2 pileft(x_{2}-x_{1}right)}{Delta varphi v}$$
Проведем вычисления:
$$
begin{array}{c}
lambda=frac{2 pi(3-2)}{3 pi} cdot 5=frac{10}{3}(m) \
T=frac{10}{3 cdot 2}=1,67(c)
end{array}
$$
Ответ. $lambda approx 3,3 mathrm{~m} ; T approx 1,67 mathrm{c}$
Читать дальше: Формула количества теплоты.
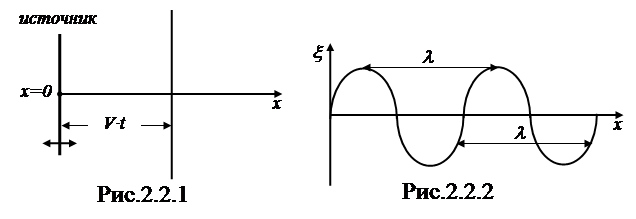





















![{displaystyle A=A_{o}cos left[2pi left({cfrac {x}{lambda }}-{cfrac {t}{T}}right)+varphi _{0}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbbfae811c4450ea2267a21ab598465200d81652)
![{displaystyle A=A_{o}cos left[2pi left({cfrac {x}{lambda }}-ftright)+varphi _{0}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bce5d0e6d62c990dae8b1db288a4f6657800a33)
![{displaystyle A=A_{o}cos left[{cfrac {2pi }{lambda }}(x-vt)+varphi _{0}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b27f3d98c223e37297aa88456f55d559aa121a24)










![{displaystyle W=Delta W_{k}+Delta W_{p}={cfrac {rho }{2}}{bigg [}left({cfrac {partial A}{partial t}}right)^{2}+v^{2}left({cfrac {partial A}{partial {x}}}right)^{2}{bigg ]}Delta V.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2140765b51b60f1c4281af0024ebb407e445bca)
![{displaystyle omega ={cfrac {W}{Delta V}}={cfrac {rho }{2}}{bigg [}left({cfrac {partial A}{partial t}}right)^{2}+v^{2}left({cfrac {partial A}{partial {x}}}right)^{2}{bigg ]}=rho A^{2}omega ^{2}sin ^{2}left(omega t-kx+varphi _{0}right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9546583574b896593dcdd8d2e65a6bfaa022d56)