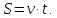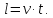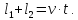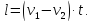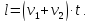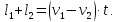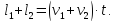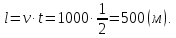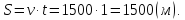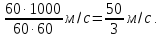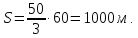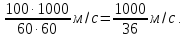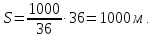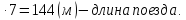Как найти длину поезда проезжающего мимо столба

Здравствуйте, дорогие читатели, подписчики и гости канала. Рассмотрим задачи на движение протяженных тел. В задачах такого типа обычно требуется определить длину одного их них. Часто встречаемые ситуации, это определить длину проезжающего поезда мимо: 1) придорожного столба; 2) лесополосы или платформы определенной длины; 3) идущего параллельно путям пешехода; 4) другого двигающего поезда или машины.

Запомни! Во всех задачах на движение используется только одна формула:

Рассмотрим несколько задач.

Задача №1. Поезд, двигаясь равномерно со скоростью 70 км/ч, проезжает мимо придорожного столба за 27 с. Найдите длину поезда в метрах.

Решение

Если поезд движется мимо столба, то он проходит расстояние равное его длине.

Время движение поезда мимо придорожного столба, переведем в часы:

Найдем длину поезда:

Задача №2 Поезд, двигаясь равномерно со скоростью 72 км/ч, проезжает мимо платформы за 15с. Длина платформы 100м. Найдите длину поезда в метрах.

Решение:

Если поезд движется мимо протяжённой лесополосы или платформы, то он проходит расстояние равное сумме длины самого поезда и платформы (лесополосы).

Задача №3

а) Поезд, двигаясь равномерно со скоростью 63 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 3 км/ч, за 39 секунд. Найдите длину поезда в метрах.

Решение

Если поезд движется мимо движущего человека, то учитываем направление движение человека. Если он движется в одну сторону с поездом, то находим разность скоростей.

б) Поезд, двигаясь равномерно со скоростью 36 км/ч, проезжает мимо пешехода, идущего параллельно путям со скоростью 4 км/ч навстречу поезду, за 54 секунды. Найдите длину поезда в метрах

Решение

Если поезд движется мимо движущего человека, то учитываем направление движение человека. Если он движется навстречу, то скорости складываются.

Задача №4 По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 40км/ч и 60км/ч. Длина товарного поезда равна 700 м. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равна 3 мин. Ответ дайте в метрах.

Решение

В этой задаче объедены несколько типов.

1) Нужно учесть, что поезда движутся в одном направлении, значит скорости будем вычитать.

2) Известна длина одного поезда, значит будем решать так же, как и с платформой.

Подставим в нашу формулу, получаем:

Задача №5 По морю параллельными курсами в одном направлении следуют две сухогруза: первый длиной 130 м, второй длиной 70м. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 16 мин после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равна 600 метров. На сколько километров в час скорость первого сухогруза меньше скорости второго.

Решение

Посмотрим, что произошло за 16 минут:

1) Второй сухогруз преодолел расстояние в 400 метров, догнав первый сухогруз; 2) Первый и второй поравнялись носами, второй преодолел расстояние в 130 метров; 3) Обогнал 1 сухогруз, где корма второго и нос первого поравнялись, преодолев расстояние в 70 м; 4) Второй отплыл от первого еще на 600 метров.

Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.

Скачать материал

без ожидания

Скачать материал

без ожидания

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Выполнила

  Ученица 11 «А» класса
  МОУ СОШ № 37
  Чеботарева Ольга
  Решение заданий ЕГЭ.
  В12.

• 

  2 слайд

  В задачах на движение протяженных тел требуется, как правило, определить длину одного из них. Наиболее типичная ситуация: определение длины поезда, проезжающего мимо столба или протяженной платформы. В первом случае поезд проходит мимо столба расстояние, равное длине поезда, во втором случае – расстояние, равное сумме длин поезда и платформы.
  Движение протяженных тел

• 

  3 слайд

  Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо придорожного столба за 30 секунд. Найдите длину поезда в метрах.
  Задание Т.6.1.

• 

  4 слайд

  Скорость движения поезда:
  V = 60 км/ч = 60000 м / 60 мин = 1000 м/мин.

  Время, за которое поезд проезжает мимо столба: t = 30 сек. = ½ мин.

  Длину поезда можно найти как пройденное расстояние: S = V ∙ t = 1000 ∙ ½ = 500 м.
  Решение:
  Ответ: 500.

• 

  5 слайд

  Поезд, двигаясь равномерно со скоростью 54 км/ч, проезжает мимо идущего параллельно путям со скоростью 6 км/ч навстречу ему пешехода за 30 секунд. Найдите длину поезда в метрах.
  Задание Т.6.2.

• 

  6 слайд

  Скорость сближения поезда и пешехода:
  V = 54 + 6 = 60 км/ч = 60000 м / 60 мин =
  = 1000 м/мин.

  Время, за которое поезд проезжает мимо столба: t = 30 сек. = ½ мин.

  Длину поезда можно найти как пройденное расстояние: S = V ∙ t = 1000 ∙ ½ = 500 м.
  Решение:
  Ответ: 500.

• 

  7 слайд

  Поезд, двигаясь равномерно со скоростью 65 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 5 км/ч пешехода за 30 секунд. Найдите длину поезда в метрах.
  Задание Т.6.3.

• 

  8 слайд

  Скорость сближения поезда и пешехода:
  V = 65 – 5 = 60 км/ч = 60000 м / 60 мин =
  = 1000 м/мин.

  Время, за которое поезд проезжает мимо столба: t = 30 сек. = ½ мин.

  Длину поезда можно найти как пройденное расстояние: S = V ∙ t = 1000 ∙ ½ = 500 м.
  Решение:
  Ответ: 500.

• 

  9 слайд

  Поезд, двигаясь равномерно со скоростью 90 км/ч, проезжает мимо лесополосы, длина которой равна 800 метрам, за 1 минуту. Найдите длину поезда в метрах.
  Задание Т.6.4.

• 

  10 слайд

  Скорость движения поезда:
  V = 90 км/ч = 90000 м / 60 мин = 1500 м/мин.

  Время, за которое поезд проезжает мимо лесополосы длиной 800 метров t = 1 мин.

  Длину поезда можно найти как пройденное расстояние S = V ∙ t = 1500 ∙ 1 = 1500 м минус длина лесополосы 800 метров:
  l = 1500 – 800 = 700 м.
  Решение:
  Ответ: 700.

• 

  11 слайд

  Человек в купе идущего со скоростью 60 км/ч пассажирского поезда, увидев идущий навстречу по параллельной колее товарный состав, засёк время, за которое тот прошёл мимо него. Найдите длину товарного состава, если это время равно 20 секундам, а скорость товарного состава равна 30 км/ч. Ответ дайте в метрах.
  Задание Т.6.5.

• 

  12 слайд

  Скорость сближения поездов:
  V = 60 + 30= 90 км/ч = 90000 м / 60 мин =
  = 1500 м/мин.

  Время, за которое состав проезжает мимо поезда: t = 20 сек. = 1/3 мин.

  Длину состава можно найти как пройденное расстояние: S = V ∙ t = 1500 ∙ 1/3 = 500 м.
  Решение:
  Ответ: 500.

• 

  13 слайд

  По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 70 км/ч и 50 км/ч. Длина пассажирского поезда равна 600 метрам. Найдите длину скорого поезда, если время, за которое он прошёл мимо пассажирского поезда, равно 30 секундам. Ответ дайте в метрах.
  Задание Т.6.6.

• 

  14 слайд

  Скорость сближения поездов:
  V = 70 + 50= 120 км/ч = 120000 м / 60 мин =
  = 2000 м/мин.

  Время, за которое скорый поезд проезжает мимо пассажирского поезда длиной 600 метров
  t = 30 с = ½ мин.

  Длину скорого поезда можно найти как пройденное расстояние
  S = V ∙ t = 2000 ∙ ½ = 1000 м
  минус длина пассажирского поезда 600 метров: l = 1000 – 600 = 400 м.

  Решение:
  Ответ: 400.

• 

  15 слайд

  По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 70 км/ч и 30 км/ч. Длина товарного поезда равна 1400 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 3 минутам. Ответ дайте в метрах.
  Задание Т.6.7.

• 

  16 слайд

  Скорость сближения поездов:
  V = 70 – 30= 40 км/ч = 40000 м / 60 мин

  Время, за которое пассажирский поезд проезжает мимо товарного поезда длиной 1400 метров t = 3 мин.

  Длину пассажирского поезда можно найти как пройденное расстояние
  S = V ∙ t = 40000 м / 60 мин ∙ 3 мин = 2000 м минус длина товарного поезда 1400 метров:
  l = 2000 – 1400 = 600 м.
  Решение:
  Ответ: 600.

• 

  17 слайд

  По морю параллельными курсами в одном направлении следуют две баржи: первая длиной 60 метров, вторая – длиной 40 метров. Сначала вторая баржа отстает от первой, и в некоторый момент времени расстояние от кормы первой баржи до носа второй баржи составляет 200 метров. Через 18 минут после этого уже первая баржа отстает от второй так, что расстояние от кормы второй баржи до носа первой равно 300 метрам. На сколько километров в час скорость первой баржи меньше скорости второй?
  Задание Т.6.8.

• 

  18 слайд

  Будем считать, что первая баржа неподвижна, а вторая приближается к ней со скоростью V (м/мин), равной разности скоростей второй и первой барж.

  Тогда за 18 минут вторая баржа проходит расстояние
  S = 200 + 60 + 40 + 300 = 600 (м).

  Поэтому V = 600 м / 18 мин =
  = 0,6 км / (18/60) ч = 0,6 ∙ 60 / 18 = 2 (км).
  Решение:
  Ответ: 2.

Краткое описание документа:

Тема задач “Движение протяжённых тел”.Данная презентация поможет учащимся качественно подготовиться к единому государственному экзамену при решении задач по данной теме .Она содержит подробное решение 8 задач .Презентация не содержит отвлекающих анимаций и картинок, поэтому учителю удобно пользоваться ею на уроке как при объяснении нового материала в 8-9 классе и даже в 6 или 7 классе, так и при  повторении текстовых задач при подготовке к единому государственному экзамену.Учитель может отдать данную презентацию учащимся для домашней работы или провести проверочную работу по задачам. 

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 251 908 материалов в базе

• Выберите категорию:
• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Задания

Версия для печати и копирования в MS Word

Задачи на движение протяженных тел

Протяженными будем считать тела, длина которых соизмерима с расстоянием, которое они проезжают.

В задачах на движение протяженных тел обычно требуется определить длину одного из них. Наиболее типичные ситуации, предлагаемые в таких задачах, – определить длину поезда проезжающего мимо:

• придорожного столба;

• идущего параллельно путям пешехода;

• лесополосы определенной длины;

• другого двигающегося поезда.

Помним, что во всех задачах на движение используется только одна формула: это формула пути

Если поезд движется мимо столба, то он проходит расстояние равное его длине. Обозначим:

l – длина поезда,

v – скорость поезда,

Если поезд движется мимо протяженной лесополосы (платформы), то он проходит расстояние равное сумме длины самого поезда и лесополосы. Обозначим:

l₁ – длина поезда,

l₂ – длина лесополосы (платформы),

v – скорость поезда,

Если поезд движется мимо движущегося человека, то учитываем направление движения человека. Если он движется навстречу, то скорости складываются, если в одну сторону, то находим разность скоростей. Обозначим:

l – длина поезда,

v₁ – скорость поезда,

v₂ – скорость человека,

В одну сторону:

В разные стороны:

Если поезд движется мимо движущегося поезда, то учитываем направление движения второго поезда. Если он движется навстречу, то скорости складываются, если в одну сторону, то находим разность скоростей. Обозначим:

l₁ – длина первого поезда,

l₂ – длина второго поезда,

v₁ – скорость первого поезда,

v₂ – скорость второго поезда,

В одну сторону:

В разные стороны:

Рассмотрим несколько задач.

Задача 1. Поезд, двигаясь равномерно со скоростью 60км/ч, проезжает мимо придорожного столба за 30 секунд. Найти длину поезда в метрах.

Решение:

v = 60 км/ч = 1000 м/мин, t = 30 сек. = 1/2 мин. Длину поезда находим как пройденное расстояние:

Ответ: 500 метров.

Задача 2. Поезд, двигаясь равномерно со скоростью 90 км/ч, проезжает мимо лесополосы, длина которой равна 800 метрам, за 1 минуту. Найти длину поезда в метрах.

Решение:

v = 90 км/ч = 1500 м/мин, t = 1 мин. Тогда пройденное поездом расстояние:

Это собственная длина поезда плюс длина лесополосы. Длина поезда равна: 1500 – 800 = 700 (м).

Ответ: 700 метров.

Задача 3. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.

Решение: Так как поезда двигаются в одном направлении, их относительная скорость равна:

v = 90 – 30 = 60 км/ч =

За 60 секунд один поезд проходит мимо другого, то есть преодолевает расстояние:

Это длина пассажирского и товарного поездов. Тогда длина пассажирского поезда равна:

1000 – 600 = 400 (м).

Ответ: 400 метров.

Задача 4. По двум параллельным железнодорожным путям навстречу друг другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошёл мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.

Решение: Так как поезда двигаются в противоположных направлениях, их относительная скорость равна:

v = 65 + 35 = 100 км/ч =

За 36 секунд один поезд проходит мимо другого, то есть преодолевает расстояние:

Это расстояние, равное сумме длин обоих поездов. Значит, длина скорого поезда равна:

1000 – 700 = 300 (м).

Ответ: 300 метров.

Задача 5.  Поезд проходит мимо неподвижного наблюдателя за 7 секунд, а мимо платформы длиной 378 метров – за 25 секунд. Найдите длину поезда. 

Решение: Из первого условия следует, что за 7 секунд поезд проедет расстояние, равное собственной длине поезда. За 25 же секунд ему надо проехать собственно саму длину платформы, т.е. 378 метров и ещё надо «вытащить» головной вагон вперед на расстояние, равное длине поезда.

1) 25 – 7 = 18 (с) – время, за которое поезд проехал 378 м

2) 378 : 18 = 21 (м/с) – скорость поезда

3) 21

Ответ: 144 м.

Задача 6. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и скорый поезда. Скорый поезд, двигаясь со скоростью 120 км/ч, догнал пассажирский поезд и прошёл мимо него за 100 секунд. Найдите скорость пассажирского поезда, если его длина составляет 800 метров, а длина скорого поезда – 700 метров. Ответ дайте в км/ч.

Решение: Считаем, что пассажирский поезд неподвижен, а скорый приближается к нему со скоростью, равной разности скоростей поездов.

1) 700 + 800 = 1500 (м) – прошёл скорый поезд за 100 секунд

2) 1500 : 100 = 15 (м/с) – разность скоростей (скорость вдогонку)

15 м/с =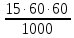 км/ч = 54 км/ч

3) 120 – 54 = 66 (км/ч) – скорость пассажирского поезда.

Ответ: 66 км/ч.

Задача 7. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 110 метров, второй — длиной 90 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 1000 метров. Через 16 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 400 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?

Решение: Пока сухогрузы перейдут из первого положения во второе, второй сухогруз переместился относительно первого на

1000 + 110 + 90 + 400 = 1600 (м).

Пусть v — разность скоростей сухогрузов, тогда

v = 1600 : 16 = 100 м/мин = 6 км/ч.

Ответ: на 6 км/ч.