В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).
- Определение куба
-
Свойства куба
- Свойство 1
-
Свойство 2
- Свойство 3
-
Формулы для куба
- Диагональ
- Диагональ грани
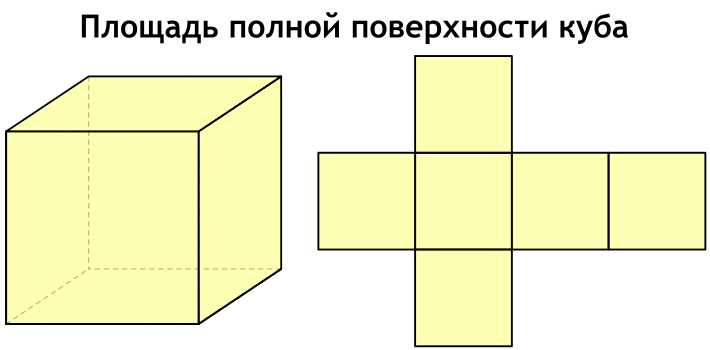
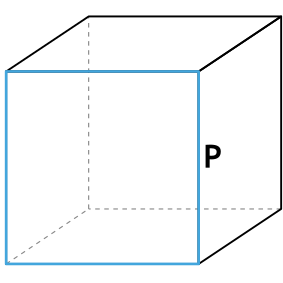
- Площадь полной поверхности
- Периметр ребер
-
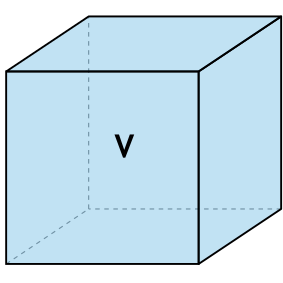
Объем
- Радиус описанного вокруг шара
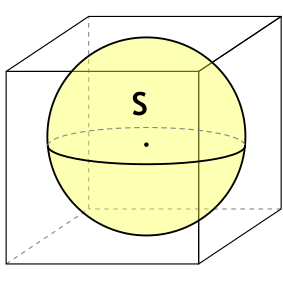
- Радиус вписанного шара
Определение куба
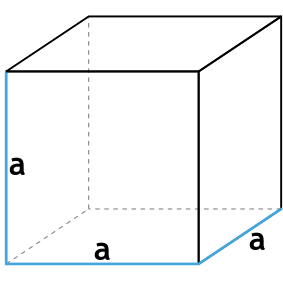
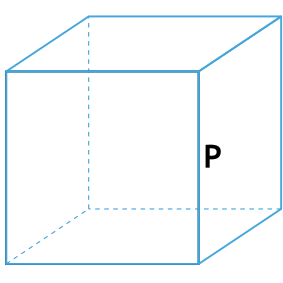
Куб – это правильный многогранник, все грани которого являются квадратами.
- Вершины куба – это точки, являющиеся вершинами его граней.
Всего их 8: A, B, C, D, A1, B1, C1 и D1. - Ребра куба – это стороны его граней.
Всего их 12: AB, BC, CD, AD, AA1, BB1, CC1, DD1, A1B1, B1C1, C1D1 и A1D1. - Грани куба – это квадраты, из которого состоит фигура.
Всего их 6: ABCD, A1B1C1D1, AA1B1B, BB1C1C, CC1D1D и AA1D1D.
Примечание: куб является частным случаем параллелепипеда или призмы.
Свойства куба
Свойство 1
Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:
- ABCD || A1B1C1D1
- AA1B1B || CC1D1D
- BB1C1C || AA1D1D
Свойство 2
Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.
- AC1 = BD1 = A1C = B1D (диагонали куба).
- О – точка пересечения диагоналей:
AO = OC1 = BO = OD1 = A1O = OC = B1O = OD.
Свойство 3
Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.
Например, на рисунке выше угол между гранями ABCD и AA1B1B является прямым.
Формулы для куба
Примем следующие обозначения, которые будут использоваться далее:
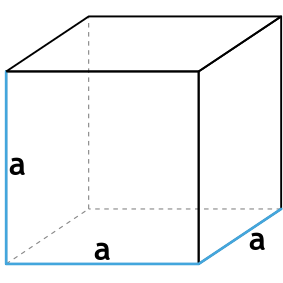
- a – ребро куба;
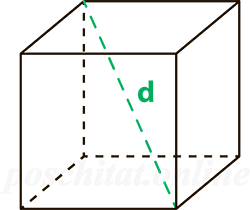
- d – диагональ куба или его грани.
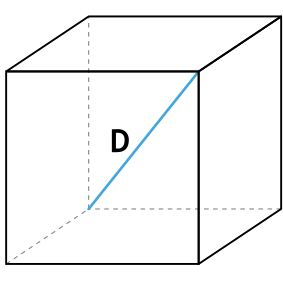
Диагональ
Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.
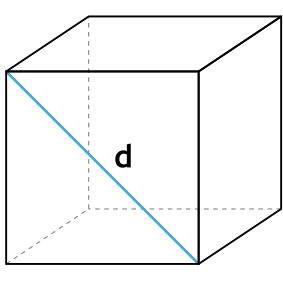
Диагональ грани
Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.
Площадь полной поверхности
Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.
Периметр ребер
Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.
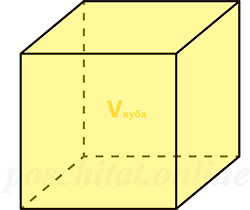
Объем
Объем куба равен длине его ребра, возведенной в куб.
Радиус описанного вокруг шара
Радиус шара, описанного около куба, равняется половине его диагонали.
Радиус вписанного шара
Радиус вписанного в куб шара равен половине длины его ребра.
Куб (или гексаэдр) — это правильный многогранник, который состоит из многоугольников, являющихся квадратами.
Онлайн-калькулятор площади поверхности куба
У куба есть двенадцать ребер, то есть, отрезков, которые являются сторонами квадратов.
Также он имеет восемь вершин и шесть граней.
У куба есть диагональ, соединяющая противоположные вершины.
Формула площади поверхности куба
Площадь поверхности куба – это сумма площадей всех его граней:
S=S1+S2+S3+S4+S5+S6S=S_1+S_2+S_3+S_4+S_5+S_6
Площадь каждой грани одинакова, то есть:
S1=S2=S3=S4=S5=S6=S′S_1=S_2=S_3=S_4=S_5=S_6=S’
S′S’ — площадь любой грани куба.
Тогда полная площадь поверхности куба запишется как:
S=6⋅S′S=6cdot S’
Рассмотрим на примерах разные способы вычисления полной площади поверхности куба.
Формула площади поверхности куба по длине ребра куба
Площадь каждой грани куба вычисляется как площадь квадрата, со стороной ребра куба по формуле:
S′=a⋅a=a2S’=acdot a=a^2
aa — сторона куба.
Отсюда, окончательно площадь поверхности куба:
S=6⋅a2S=6cdot a^2
aa — длина стороны куба.
Найти площадь поверхности куба, если длина его ребра равна 12 (см.).
Решение
a=12a=12
S=6⋅a2=6⋅122=6⋅144=864S=6cdot a^2=6cdot 12^2=6cdot 144=864 (см. кв.)
Ответ: 864 см. кв.
Формула площади поверхности куба по диагонали куба
По теореме Пифагора, диагональ куба связанна с длиной его ребра по формуле:
d2=a2+a2+a2d^2=a^2+a^2+a^2
d2=3⋅a2d^2=3cdot a^2
d=3⋅ad=sqrt{3}cdot a
Отсюда:
a=d3a=frac{d}{sqrt{3}}
Подставим в формулу для площади:
S=6⋅a2=6⋅(d3)2=2⋅d2S=6cdot a^2=6cdotBig(frac{d}{sqrt{3}}Big)^2=2cdot d^2
S=2⋅d2S=2cdot d^2
dd — диагональ куба.
Одна четвертая часть диагонали куба равна 2 (см.). Найти площадь поверхности куба.
Решение
14⋅d=2frac{1}{4}cdot d=2
Найдем диагональ:
d=4⋅2=8d=4cdot 2=8
Площадь:
S=2⋅d2=2⋅82=2⋅64=128S=2cdot d^2=2cdot 8^2=2cdot 64=128 (см. кв.)
Ответ: 128 см. кв.
Формула площади поверхности куба по длине диагонали квадрата (грани куба)
По теореме Пифагора, диагональ квадрата ll связанна с его стороной aa:
l2=a2+a2l^2=a^2+a^2
l2=2⋅a2l^2=2cdot a^2
l=2⋅al=sqrt{2}cdot a
Тогда сторона квадрата:
a=l2a=frac{l}{sqrt{2}}
Подставляем в формулу для площади и получаем:
S=6⋅a2=3⋅l2S=6cdot a^2=3cdot l^2
S=3⋅l2S=3cdot l^2
ll — диагональ квадрата (грани куба).
Одна четвертая часть диагонали квадрата равна 1 (см). Найти площадь поверхности куба, образованного данным четырехугольником.
Решение
14⋅l=1frac{1}{4}cdot l=1
Найдем диагональ квадрата:
l=4⋅1=4l=4cdot 1=4
Тогда площадь:
S=3⋅l2=3⋅42=48S=3cdot l^2=3cdot 4^2=48 (см. кв.)
Ответ: 48 см. кв.
Разберем более сложные примеры.
Формула площади поверхности куба по площади вписанного в куб шара
В куб вписан шар площади SшарS_{text{шар}}. Тогда радиус RR этого шара равен половине длины стороны куба aa:
R=a2R=frac{a}{2}
Площадь шара дается формулой:
Sшар=4⋅π⋅R2S_{text{шар}}=4cdotpicdot R^2
Отсюда найдем радиус шара:
R=Sшар4⋅πR=sqrt{frac{S_{text{шар}}}{4cdotpi}}
Сторона грани куба:
a=2⋅R=2⋅Sшар4⋅πa=2cdot R=2cdotsqrt{frac{S_{text{шар}}}{4cdotpi}}
Наконец площадь поверхности куба:
S=6⋅a2=6⋅SшарπS=6cdot a^2=frac{6cdot S_{text{шар}}}{pi}
S=6⋅SшарπS=frac{6cdot S_{text{шар}}}{pi}
SшарS_{text{шар}} — площадь шара, вписанного в куб.
В куб вписан шар, площадь которого равна 64 “пи” (см. кв.). Найти полную площадь поверхности куба.
Решение
Sшар=64πS_{text{шар}}=64pi
По формуле:
S=6⋅Sшарπ=6⋅64⋅ππ=384S=frac{6cdot S_{text{шар}}}{pi}=frac{6cdot 64cdotpi}{pi}=384 (см. кв.)
Ответ: 384 см. кв.
Не знаете, кто сможет решить контрольную работу на заказ для вас? Наши эксперты с удовольствием окажут вам помощь!
Тест по теме “Площадь поверхности куба”

{S_{полн}=6a^2}
На этой странице мы собрали формулы, которые помогут найти площадь полной и боковой поверхности куба. А чтобы упростить расчет у нас есть калькулятор, который сделает это быстро и точно.
В дополнение на сайте можно найти объем куба.
Куб – фигура, представляющая собой правильный многогранник, все грани которого являются квадратами. Все ребра (стороны) куба равны между собой.
Содержание:
- калькулятор площади поверхности куба
- площадь полной поверхности куба
- формула площади полной поверхности куба через ребро
- формула площади полной поверхности куба через диагональ грани
- формула площади полной поверхности куба через диагональ куба
- формула площади полной поверхности куба через периметр грани
- формула площади полной поверхности куба через периметр куба
- формула площади полной поверхности куба через объем
- формула площади полной поверхности куба через площадь вписанного шара
- площадь боковой поверхности куба
- формула площади боковой поверхности куба через ребро
- формула площади боковой поверхности куба через диагональ грани
- формула площади боковой поверхности куба через диагональ куба
- формула площади боковой поверхности куба через периметр грани
- формула площади боковой поверхности куба через периметр куба
- формула площади боковой поверхности куба через объем
- примеры задач
Что такое площадь полной поверхности куба
Куб состоит из сторон, которые называют гранями. Каждая такая грань представляет собой квадрат, а всего у куба 6 граней. Площади всех этих граней равны между собой и сложив все площади всех шести граней куба мы получим площадь полной поверхности куба.
Площадь полной поверхности куба – это сумма площадей всех его граней.
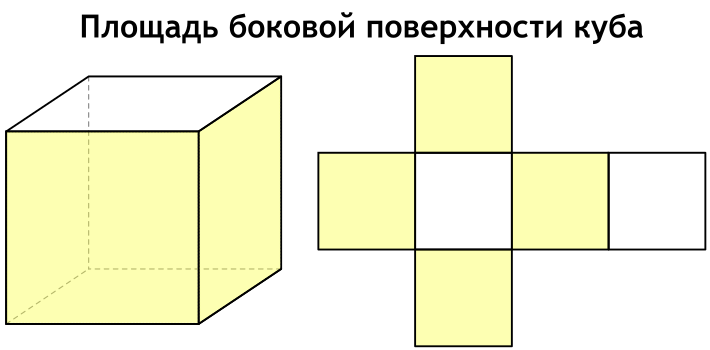
Площадь полной поверхности удобно представить, если посмотреть на развертку куба.
Формула площади полной поверхности куба через ребро
{S_{полн}=6a^2}
a – ребро куба
Формула площади полной поверхности куба через диагональ грани
{S_{полн}=3d , ^2}
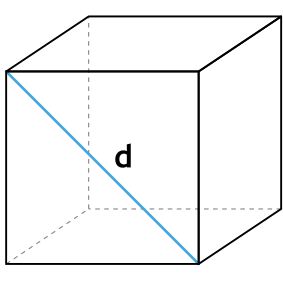
d – диагональ грани куба
Формула площади полной поверхности куба через диагональ куба
{S_{полн}=2D^2}
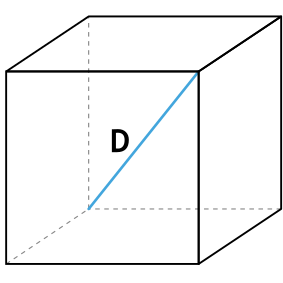
D – диагональ куба
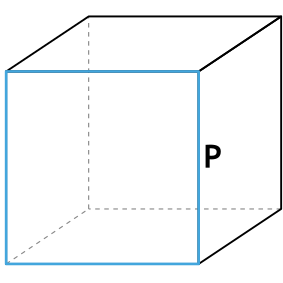
Формула площади полной поверхности куба через периметр грани
{S_{полн}= dfrac{3}{8}P^2}
P – периметр грани куба
Формула площади полной поверхности куба через периметр куба
{S_{полн}= dfrac{P^2}{24}}
P – периметр куба
Формула площади полной поверхности куба через объем
{S_{полн}= 6{(sqrt[3]{V})}^2}
V – объем куба
Формула площади полной поверхности куба через площадь вписанного шара
{S_{полн}= 6 dfrac{S}{pi}}
S – площадь вписанного в куб шара
Что такое площадь боковой поверхности куба
Боковая поверхность куба – сумма площадей всех его боковых граней, которых у куба четыре.
Формула площади боковой поверхности куба через ребро
{S_{бок} = 4a^2}
a – ребро куба
Формула площади боковой поверхности куба через диагональ грани
{S_{бок}=2d , ^2}
d – диагональ грани куба
Формула площади боковой поверхности куба через диагональ куба
{S_{бок}=dfrac{4}{3}D^2}
D – диагональ куба
Формула площади боковой поверхности куба через периметр грани
{S_{бок}= dfrac{P^2}{4}}
P – периметр грани куба
Формула площади боковой поверхности куба через периметр куба
{S_{бок}= dfrac{P^2}{36}}
P – периметр куба
Формула площади боковой поверхности куба через объем
{S_{бок}= 4{(sqrt[3]{V})}^2}
V – объем куба
Примеры задач на нахождение площади поверхности куба
Задача 1
Найдите площадь поверхности куба, если его объем равен 125см³.
Решение
Для нахождения площади полной поверхности куба через его объем, нам поможет эта формула.
S_{полн} = 6{(sqrt[3]{V})}^2 = 6{(sqrt[3]{125})}^2 = 6{(5)}^2 = 6 cdot 25 = 150 : см²
Ответ: 150 см²
Проверить ответ нам поможет калькулятор .
Задача 1
Найдите площадь боковой поверхности куба с ребром 4см.
Решение
Для нахождения площади боковой поверхности куба с известной длиной ребра используем эту формулу.
S_{бок} = 4a^2 = 4 cdot 4^2 = 4 cdot 16 = 64 : см²
Ответ: 64 см²
Проверка .
Площадь поверхности куба
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь поверхности куба
Чтобы посчитать площадь поверхности куба воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чему равна площадь поверхности куба, если:
длина ребра a =
Sпов =
0
Округление ответа:
Чему равна площадь поверхности куба, если:
длина диагонали d =
Sпов =
0
Округление ответа:
Чему равна площадь поверхности куба, если:
объём Vкуба =
Sпов =
0
Округление ответа:
Теория
Площадь поверхности куба через ребро
Чему равна площадь поверхности куба Sпов, если длина его ребра a:
Формула
Sпов = 6 ⋅ a²
Пример
Для примера, посчитаем чему равна площадь поверхности куба, если он имеет длину рёбер a = 5 см :
Sпов = 6 ⋅ 5² = 6 ⋅ 25 = 150 см²
Площадь поверхности куба через диагональ
Чему равна площадь поверхности куба Sпов, если длина диагонали этого куба d:
Формула
Sпов = 2 ⋅ d²
Пример
Для примера, посчитаем чему равна площадь поверхности куба, если длина диагонали у него d = 3 м:
Sпов = 2 ⋅ 3² = 2 ⋅ 9 = 18 м² = 180 000 см²
Площадь поверхности куба через объем
Чему равна площадь поверхности куба Sпов, если объём куба Vкуба:
Формула
Sпов = 6 ⋅ ³√Vкуба²
Пример
Для примера, посчитаем чему равна площадь поверхности куба, если его объём Vкуба = 8 см³:
Sпов = 6 ⋅ 3√8² = 6 ⋅3√64 = 6 ⋅ 4 = 24 см²
См. также
Формулы?
Площадь поверхности куба равна сумме площадей шесть квадратов, которые и составляют поверхность куба.
Площадь каждого такого квадрата, которые являются гранями данного куба, вычисляются по формуле:
, где а – длина ребра квадрата.
Чтобы найти площадь всей поверхности квадрата, надо найти сумму площадей всех шести его граней или просто, умножить площадь одной из граней на 6.
Вот так можно вывести формулу вычисления площади поверхности куба:
модератор выбрал этот ответ лучшим
Турук Макто
[55.4K]
9 лет назад
Я формул не помню, если они специально какие-то есть. Но давайте по логике. Если сторона одна – это квадрат, то сторона умножается на сторону – это будет площадь квадрата. И таких квадратов шесть штук. Вот собственно и всё. Сторона в квадрате шесть раз! 6*а*а.
MarkTolkien
[85.3K]
9 лет назад
Для того, чтобы найти площадь поверхности куба, нужно вычислить площадь грани. Площадь одной грани – длина ребра в квадрате, то есть во второй степени. У куба шесть сторон (граней), поэтому площадь одной множим на 6.
Ракитин Сергей
[450K]
9 лет назад
У куба шесть граней, каждая из которых представляет собой квадрат. Если сторона куба равна a, то площадь его поверхности будет равна 6a^2. В справочниках эту формулу обычно не приводят в силу её очевидности.
Асюшка
[101K]
9 лет назад
Так как грани куба – это квадраты. И куб состоит из шести таких граней, то получается, что чтобы найти площадь поверхности куба, нам необходимо для начала найти площадь квадрата(грани куба) умножаем на 6 (6 граней). Ой, сейчас сама запутаюсь и Вас запутаю, проще, действительно, формулой записать:
S (площадь куба) = 6 * а2 (площадь одной грани – квадрата).
Медвед
[141K]
9 лет назад
Куб – это параллелепипед, у которого все стороны равны. Значит, каждая из граней куба является квадратом, и все эти квадраты равны между собой. Если обозначить сторону куба как Н, площадь одного квадрата будет (Н)в квадрате. Таких квадратов 6. Поэтому имеем формулу для определения поверхности куба S:
S=6x[(Н)в квадрате]
Samborskaya
[7K]
9 лет назад
Площадь поверхности куба складывается из всех площадей его сторон. Каждая сторона представляет из себя квадрат, а площадь квадрата равна произведению его сторон. Пусть сторона квадрата равна Х, тогда площадь всей поверхности куба вычисляется как S = 6 * X * X.
Любовь7800
[4K]
9 лет назад
И без формул даже можно, если нужно измерить все поверхности, то найти площать одной, умножив одну сторону на другую и потом умножить на шесть. Так ка у куда все стороны равны, то можно одну сторону умножить сразу на 12, так как граней 12.
Радуга-Весна
[50.4K]
9 лет назад
Площадь поверхности куба равняется шесть умножить на квадрат длины грани куба.
А вот и сама формула площади куба
S = 6* a2
S – это площадь куба,
a – это длина грани куба.
Как видно площадь куба рассчитывается совсем просто.
Solnce lychik
[40.9K]
9 лет назад
Эту площадь учили еще в школе. А формула выглядит так:
s=6*a2
где s-площадь куба
a-длина грани
Если честно без интернета я бы это и не вспомнила.
Да все что учила в школе со временем забывается. А вспомнить очень сложно.
Знаете ответ?