Элементы
трассы автомобильной дороги, виды
закруглений, угол поворота трассы
Трассой
называется
спроецированную и проложенную на
местности ось дороги. Для проектирования
трассу представляют в виде двух основных
частей: план трассы и продольный профиль.
План трассы
– это ее проекция на горизонтальную
плоскость, а продольный
профиль –
линия земной поверхности, образованная
в результате сечения ее горизонтальной
плоскостью, проходящей по трассе.
Различают
основные элементы плана:
прямые участки
и (закругления – простые (круговые
кривые и клатоиды), сложные (сопряжение
нескольких кривых разных радиусов),
биклотоиды
(округления из 2х клатоид)). Основные
элементы продольного профиля :прямые
и вертикальные
кривые.
Вертикальные кривые в виде круговых
или клатоидных прямых. Главные
точки –
элементы трассы с разными законами
движения. Вспомогательные
точки –
вершины углов поворота и середины
закругления. Углом
поворота трассы
– угол между предыдущим и последовательным
направлением трассы .
11.Расчет основных элементов закруглений автомобильных дорог.
Круговая
кривая характеризуется углом поворота
трассы а
и радиусом
К.
Радиус круговой кривой устанавливают
при проектировании в зависимости от
условий местности и расчетной скорости
движения транспортных средств, а угол
поворота измеряют на карте, плане или
непосредственно на местности.
Основные
элементы для разбивки круговой кривой:
тангенс – Г, биссектриса – Б,
кривая – К,
домер – Б
– легко
определяются из рис.
Центральный
угол круговой кривой равен углу поворота
трассы а.
Отрезок О
ВУ является
осью симметрии и делит центральный угол
пополам.
Главные
точки НК и КК;;
K=R*
α
«в радианах»
Тангенс
– это элемент кривой и в этом смысле его
еще называют дорожным тангенсом.
Т
= R*tgα/2
Биссектрисой
называют отрезок от вершины угла ВУ до
середины кривой СК. Вначале из
прямоугольного треугольника О
НК ВУ находят
длину отрезка О ВУ
Б=(ВУ-0)-(ВУ-СК); Б=R/cos
α/2
– R=
R(sec
α/2-1);
Кривая
– длина круговой кривой
К=πRα/180
= Rα/ρ;
ρ–
число градусов в радианах;
Домер
– разность длин ломаной линии НК – ВУ –
КК и кривой К.
D=2T–K
Стрела
прогиба
12. Восстановление и закрепление трассы.
Начинают
восстановление трассы с отыскания на
местности вершин углов поворота. Вершины,
на которых не сохранились знаки крепления,
возобновляют по абрисам и сохранившемуся
пикетажу или по схемам их привязки
соответствующими промерами от местных
предметов. Можно восстановить положение
вершины прямой засечкой по проектным
углам из сохранившихся соседних вершин.
Если
знаки крепления не сохранились на
нескольких подряд расположенных вершинах
и их нельзя восстановить от местных
предметов, то такой участок трассируют
вновь. Величины углов поворота и
расстояния между вершинами принимают
из проекта.
При
восстановлении трассы заново измеряют
углы поворота и сравнивают их с проектными.
Если обнаруживаются большие расхождения,
положение трассы на местности не
изменяют, а вносят изменения в проектные
углы и пересчитывают все элементы кривых
по исправленному углу.
Вновь
измеряют длины линий и в створе по
прибору восстанавливают пикеты. При
обнаружении промахов в прежней разбивке
(например, пропущена лента при
трассировании) или при значительном
накоплении ошибок (более 1 м) сплошное
смещение пикетов не делают, а устанавливают
так называемые рубленные, меньше 100 м,
пикеты. Так поступают для того, чтобы
восстанавливаемый пикетаж соответствовал
разбитому при трассировании, по которому
составлен проектный профиль, иначе
рабочие отметки не будут соответствовать
полученным в проекте. ьДля проверки
профиля трассы и уточнения объемов
земляных работ выполняют контрольное
нивелирование. В него включают все
пикеты и плюсовые точки и всю сеть
постоянных и временных реперов. При
нивелировании определяют отметки вновь
устанавливаемых рабочих реперов. Если
отметки точек при контрольном нивелировании
отличаются более чем на 4-5 см, профиль
исправляют и определяют новые рабочие
отметки.Закрепление
трассы на местности Все
проектные точки трассы, вынесенные в
натуру, должны быть надежно закреплены.
Пикеты и плюсовые точки, главные и
промежуточные точки закруглений
закрепляют с помощью кольев и сторожков.
Вершины углов поворота и створные точки
на прямых участках в пределах взаимной
видимости через 0,5 – 1 км закрепляют
деревянными или железобетонными
столбами, металлическими уголками и
т.п. На застроенных территориях эти
точки привязывают линейными промерами
к постоянным объектам. На закруглениях
трассы производят детальную разбивку
переходных и круговых кривых.. С помощью
теодолитаа пикетаж выносят перпендикулярно
оси дороги, а главные точки кривых
перпендикулярно линиям соответствующих
тангенсов. Пикеты на кривой закрепляют
перпендикулярно к касательной в данной
точке. Для закрепления применяют бетонные
и деревянные столбики и колья.Выносимые
точки трассы закрепляют двумя знаками,
образующими створ. Их располагают обычно
с одной, нагорной стороны, а иногда и по
разные стороны от оси дороги. Пользуясь
таким створом, можно быстро и точно
восстановить при строительстве точки
на трассе. Расстояния от оси до первых
створных точек принимают постоянными,
равными 10 – 15 м, иногда и более. Вторые
створные точки закрепляют на расстоянии
5 – 15 м от первых. Обычно на четных пикетах
выноски устанавливают из столбов, а на
нечетных из кольев. Измеряют расстояния
от трассы до выносных точек и записывают
их в журнал или на схему закрепления
трассы. Каждую выносную точку подписывают
масляной краской на столбе или на
сторожке, указывая наименование знака,
в какую сторону от оси по ходу пикетажа
и на какое расстояние он вынесен.
Например, “Вын. ПК 31 пр. 15”. Знаки
окапывают.
На
каждой вершине угла поворота устанавливают
столб, с забитым сверху в торец гвоздем,
для центрирования прибора. Этот столб
окапывают и обсыпают земляным холмиком.
По направлению биссектрисы с внешней
стороны примерно на расстоянии 1 м
устанавливают указательный столб, на
котором, на стороне, обращенной к вершине,
выписывают номер и величину угла и
его пикетажное положение. Кроме того,
положение вершины угла поворота
закрепляют четырьмя выносными столбами
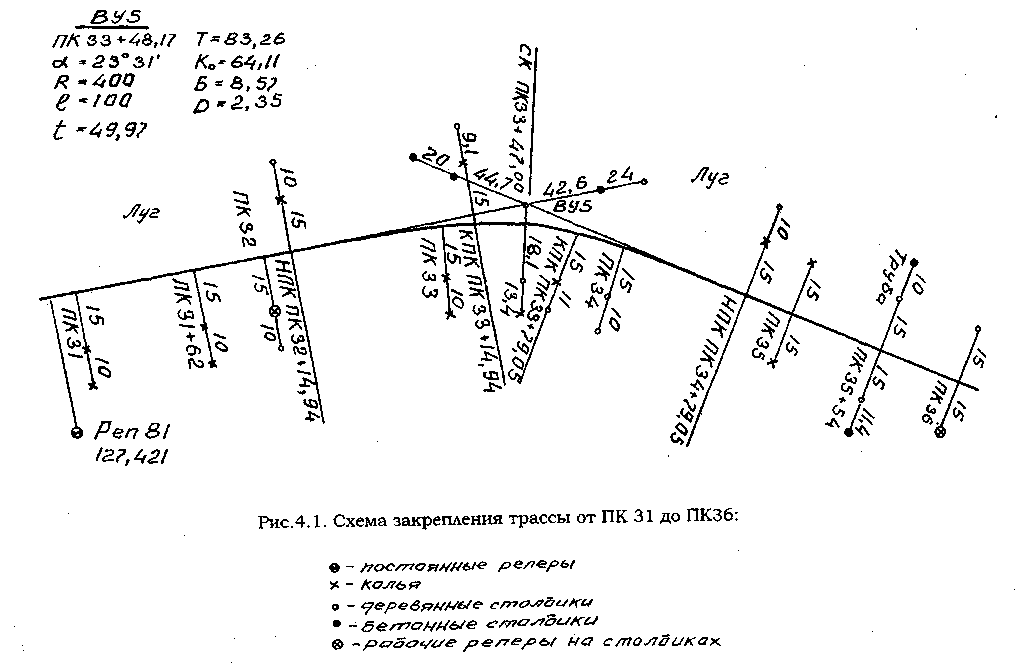
по продолжению линий тангенсов (см.
рис.4.1) или по линии биссектрисы по разные
стороны вершины. Расстояние между
вершиной угла поворота и выносной точкой
должно быть не менее 20 м. Середину кривой
закрепляют по линии биссектрисы.Малые
искусственные сооружения закрепляют
створными знаками по их оси. На рис.4.1
показано закрепление водопропускной
трубы на ПК 35+54. Закрепляют также
пересечения трассы с дорогами.
Одновременно
с закреплением трассы для удобства
ведения строительных работ сгущают
сеть рабочих реперов, устанавливая их
за пределами зоны работ через 4-5 пикетов,
у каждого искусственного сооружения,
у высоких (свыше 3 м ) насыпей и глубоких
(более 3 м) выемок [21 ] с таким расчетом,
чтобы их было не менее четырех на 1 км.
В качестве рабочих реперов используют
оголовки столбов выносных точек,
установленных ниже глубины промерзания,
пни деревьев твердых пород, цоколи
зданий, опоры мостов и другие местные
предметы, устойчивые по высоте. Места
постановки нивелирной рейки на реперах
должны быть точно обозначены гвоздем
или краской.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Круговые кривые. Железнодорожные линии (также и автомобильные дороги) в плане состоят из прямолинейных участков, сопряжённых между собой кривыми. Наиболее простой и распространённой формой кривой является дуга окружности. Такие кривые носят название круговых кривых. На железных дорогах применяют круговые кривые со следующими радиусами: 4000, 3000, 2000, 1800, 1500, 1200, 1000, 800, 700, 600, 500, 400 и 300 м. Радиус кривой выбирают при проектировании дороги, руководствуясь конкретными техническими условиями.
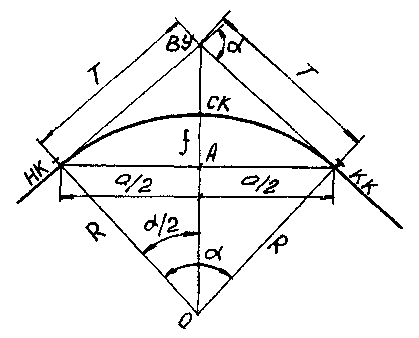
Главными точками кривой, определяющими её положение на местности, являются вершина угла ВУ, начало кривой НК, середина кривой СК и конец кривой КК (рис. 15.3).
![inj_geo_2-114.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-114.jpg)
Рис. 15.3 Схема круговой кривой
Основные элементы кривой – её радиус R и угол поворота a. К основным элементам относятся также:
– тангенс кривой Т (или касательная) – отрезок прямой между вершиной угла и началом или концом кривой;
– кривая К – длина кривой от начала кривой до её конца;
– биссектриса кривой Б – отрезок от вершины угла до середины кривой;
– домер Д – разность между длиной двух тангенсов и кривой.
Во время изысканий угол a измеряют, а радиус R назначают. Остальные элементы вычисляют по формулам, вытекающим из прямоугольного треугольника с вершинами ВУ, НК, О (центр окружности):
Т = R×tg(a/2); К = R×a = p R a°¤180°; Б = R [sec(a/2) – 1], (15.1)
где a° – угол поворота в градусах.
Домер вычисляют по формуле
. (15.2)
Вместо вычислений по формулам можно воспользоваться таблицами для разбивки кривых на железных дорогах, где по заданным радиусу и углу поворота сразу находят значения Т, К, Б и Д.
В месте поворота трассы пикетаж ведётся по кривой. Пикетажное положение главных точек кривой определяют по формулам:
ПК НК = ПК ВУ – Т; ПК КК = ПК НК + К; ПК СК = ПК НК + К/2. (15.3)
Правильность вычислений контролируют по формулам:
ПК КК = ПК ВУ + Т – Д; ПК СК = ПК ВУ + Д/2. (15.4)
Пример.
Измерено a = 18°19¢ и задан радиус R = 600 м. Вершина угла расположена на пикете 6 + 36,00.
По формулам (15.1) и (15.2) или по таблицам находим элементы кривой: Т = 96,73 м; К = 191,81 м; Д = 1,65 м; Б = 7,75 м.
Вычислим пикетажное положение главных точек:
Контроль:
ПК ВУ 6 + 36,00 ПК ВУ 6 + 36,00
– Т 96,73 + Т 96,73
ПК НК 5 + 39,27 7 + 32,73
+ К 1 + 91,81 – Д 1,65
ПК КК 7 + 31,08 ПК КК 7 + 31,08
ПК НК 5 + 39,27 ПК ВУ 6 + 36,00
+ К/2 95,90 – Д/2 0,82
ПК СК 6 + 35,17 ПК СК 6 + 35,18
Переходные кривые. Непосредственное сопряжение прямого участка пути с круговой кривой приводит к тому, что во время движения поезда в месте сопряжения внезапно возникает центробежная сила F, прямо пропорциональная квадрату скорости движения v и обратно пропорциональная радиусу кривой . Чтобы обеспечить постепенное нарастание центробежной силы, между прямой и круговой кривой вставляют переходную кривую, радиус кривизны r которой плавно изменяется от ¥ до R. Если положить, чтобы центробежная сила менялась пропорционально расстоянию s от начала кривой, то получим
![inj_geo_2-117.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-117.jpg)
где s и r – текущие значения расстояния от начала переходной кривой и ее радиуса кривизны;
R – радиус кривизны в конце переходной кривой.
Индексом k отмечены значения переменных в конце переходной кривой.
Для радиуса кривизны переходной кривой в текущей точке i найдём:
r = lR/s, (15.5)
где через l обозначена длина переходной кривой sk. Кривая, описываемая уравнением (15.5), в математике называется клотоидой, или радиоидальной спиралью.
Угол поворота трассы на переходной кривой. На бесконечно малом отрезке кривой ds (рис. 15.4, а) происходит поворот трассы на угол
.
Подставляя выражение радиуса кривизны r из (15.5), получим
.
Выполним интегрирование от начала кривой НК, где j = 0 и s = 0, до текущей точки i:
![inj_geo_2-120.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-120.jpg)
откуда
Rlj = s2/2.
б)
а)
![inj_geo_2-121.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-121.jpg)
Рис. 15.4 Схема переходной кривой:
а – углы поворота трассы: φ – в текущей точке i, β – в конце
переходной кривой (точка КПК); б – приращения координат
Из полученного уравнения вытекают формулы:
![inj_geo_2-122.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-122.jpg)
![inj_geo_2-123.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-123.jpg)
где b – угол поворота трассы в конце переходной кривой;
l – длина переходной кривой;
R – радиус кривизны в конце переходной кривой, равный радиусу следующей за нею круговой кривой.
Координаты точки переходной кривой. Совместим начало координат с началом переходной кривой и направим ось x по касательной к ней (см. рис. 15.4, а). Бесконечно малому приращению дуги кривой соответствуют бесконечно малые приращения координат (рис. 15.4, б):
dx = cosj×ds; dy = sinj×ds. (15.7)
Разложим синус и косинус в ряд и, удержав в разложениях по два члена, подставим в них выражения для j из (15.6):
cosj = 1-j2/2 = 1 – s4/(8R2l2);
sinj = j – j3/6 = s2/(2Rl) – s6/(48R3l3).
Подставляя полученные выражения в (15.7) и выполняя интегрирование, найдём:
![inj_geo_2-124.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-124.jpg)
![inj_geo_2-125.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-125.jpg)
![inj_geo_2-126.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-126.jpg)
![inj_geo_2-127.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-127.jpg)
Смещение начала кривой (сдвижка). На рис. 15.5 дуга НК-КПК представляет собой переходную кривую, переходящую после точки КПК в круговую. Продолжим круговую кривую до точки Q, где её направление, параллельно оси x. Обозначим через m смещение, параллельное оси x, начала переходной кривой относительно точки Q, в которой начиналась бы круговая кривая при отсутствии переходной. Через p обозначим смещение в перпендикулярном направлении. Из рис. 15.5 видно:
,
где xКПК и yКПК – координаты конца переходной кривой, вычисляемые по формулам (15.8) и (15.9) с аргументом s = l .
Сочетание круговой кривой с переходными. На рис. 15.6 показана кривая, поворачивающая трассу на угол a и состоящая из круговой части с радиусом R и двух переходных кривых одинаковой длины l.
|
|
|
|
Рис. 15. 5 Смещение начала переходной кривой |
Рис. 15.6 Сопряжение круговой кривой с переходными |
Если бы не было переходных кривых, в образованный прямыми линиями трассы угол была бы вписана дуга окружности радиуса R, равная Q-СК-Q1 и имеющая длину K = Ra.
При наличии переходных кривых на каждой из них происходит поворот трассы на угол b, отчего на долю круговой кривой приходится поворот на угол a-2b. Поэтому суммарная длина кривой равна
Kc = R (a-2b) + 2l = Ra – 2Rb + 2l = K – l + 2l = K + l.
Тангенс и биссектриса определяются по формулам:
Тс = T + m + Tp; Бc = Б + Бp,
где Тp = ptg(a/2); Бp = psec(a/2).
Домер в этом случае равен
.
В полевых условиях значения m, Тp и Бp вычисляют на микрокалькуляторе или выбирают из таблиц для разбивки кривых на железных дорогах. Пикетажное положение главных точек кривой вычисляют по формулам, аналогичным (15.3) и (15.4).
Что такое радиус разворота, каким он бывает, и почему он важен?
При выборе автомобиля обычно смотрят на его ключевые характеристики: размер, объем и мощность двигателя, тип трансмиссии и так далее. Однако в повседневной жизни есть и другие показатели, которые оказываются весьма важными – к примеру, радиус разворота. На что влияет это значение, как его замеряют, и почему важно не запутаться в этом, казалось бы, элементарном понятии?
К ак нетрудно догадаться, радиус разворота – это радиус полуокружности, которую описывает автомобиль при развороте с места на 180 градусов при условии, что руль повернут до упора. Правда, как мы убедимся чуть ниже, само словосочетание «радиус разворота» весьма коварное.
Радиус разворота – показатель, во многом отражающий маневренность автомобиля. Чем он больше, тем больше места требуется автомобилю для совершения полного разворота на 180 градусов – то есть, в условиях, когда ширина дороги известна и ограничена, этот показатель отражает то, сможете ли вы развернуться на ней в один прием, или же придется сдавать назад и быстро крутить рулем на втором (а то и третьем) заходе. Однако очевидно, что сам по себе радиус разворота говорит не только о способности развернуться, но и о том, насколько маневренным является автомобиль: чем меньше это значение, тем удобнее будет управлять машиной в стесненных условиях и легче парковаться.
Даже для замера этого элементарного на первый взгляд показателя существует две методики: «от бордюра до бордюра» и «от стены до стены».
Первый отражает радиус полуокружности, которую описывают колеса автомобиля при развороте: то есть, чтобы его замерить, нужно отметить мелом стартовое положение наружного (относительно поворота) колеса, затем вывернуть руль до упора, развернуться на 180 градусов, отметить мелом конечную точку, замерить расстояние между ними и разделить его пополам. Соответственно, эта методика замера отражает, какой должна быть ширина гладкой дороги, чтобы автомобиль смог развернуться, не съехав с нее.
Однако в реальной жизни стоит учитывать тот факт, что у автомобиля есть передний свес – то есть, расстояние от оси передних колес до конца переднего бампера. И если дорога, к примеру, ограничена высокими бордюрами, то развернуться на ней, даже «укладываясь» по показателю от бордюра до бордюра, не выйдет: автомобиль упрется в препятствие выступающим вперед бампером. Для отражения этого «реального» радиуса разворота используют показатель «от стены до стены»: соответственно, чтобы замерить его, нужно закрепить мел на стержне, установленном на наружном (относительно поворота) углу бампера автомобиля, затем выполнить разворот, замерить диаметр получившейся полуокружности и разделить его пополам.
Разумеется, автопроизводители стремятся показать свои автомобили максимально маневренными, так что в брошюрах и списках характеристик практически всегда указывается радиус разворота от бордюра до бордюра, так как он меньше, чем от стены до стены. В реальной жизни, сравнивая машины по показателю маневренности, стоит учитывать не только на эту цифру, но и длину переднего свеса.
Главная проблема, связанная с радиусом разворота, заключается в том, что само словосочетание «радиус разворота» является скорее разговорным, ведь реальный показатель, отражающий расстояние, необходимое для разворота «от упора до упора» – это диаметр. Соответственно, при перечислении габаритных и технических характеристик автомобиля зачастую указывают именно его, хотя можно встретить и радиус. Но главное при этом – не перепутать эти два показателя. Ведь даже сами производители порой ошибаются: к примеру, в пресс-релизе о новом Land Cruiser Prado в Toyota говорят о том, что он «сохранил удобный диаметр разворота, составляющий всего 5,8 м», что для машины длиной в 4,84 метра выглядит явно невозможным. А вот в брошюре по модели указано, что это «минимальный радиус разворота по колесам», что уже похоже на правду. Чтобы в этом убедиться, можно заглянуть, к примеру, на австралийский официальный сайт, где указан уже не радиус, а диаметр разворота, равный 11,6 метра.
Несложно догадаться, что радиус разворота зависит прежде всего от габаритных размеров автомобиля и угла поворота передних колес. Габариты машины поменять, очевидно, нельзя, а угол поворота колес на гражданских автомобилях ограничен параметрами работы рулевого управления, а на машинах с приводом на переднюю ось еще и рабочими диапазонами шарниров равных угловых скоростей (ШРУС, или «гранат»), которые крайне не любят работать при вывернутых колесах. Поэтому, не углубляясь в теорию, можно ответить так: без вмешательства в конструкцию с потерей гарантии нормальной работоспособности изменить радиус разворота машины нельзя.
Наглядным примером «вмешательства в конструкцию» можно считать автомобили, подготовленные для соревнований по дрифту: у них угол поворота передних колес («выворот») стараются сделать максимальным. Но нужно это уже не для уменьшения радиуса разворота, а для того, чтобы поддерживать как можно больший угол заноса при движении в повороте – то есть, это делается отнюдь не для улучшения показателей «гражданской» эксплуатации.
Источник
Расчет радиуса поворота фуры
Во время движения большегрузных автомобилей, особенно фур с прицепом, у которых линейные размеры 20 м и больше, происходят другие физические процессы при выполнении поворота, чем у легкового транспорта или автобусов. В специальной литературе эти технологические движения описаны тщательно, приведены схемы и рисунки. Некоторые нюансы постараемся доходчиво объяснить читателям в этой статье.
Что такое радиус поворота
Многие автолюбители «не в теме», и редко кто из них знает, что такое радиус поворота фуры. Согласно специальной технической литературе – это воображаемая дуга, по линии которой перемещается центр тяжести тягача с полуприцепом при выполнении сложного маневрирования. Максимальное значение этой величины (радиуса) во многом зависит от специфической конструкции транспортного средства.
Вот как фура во время поворота может зацепить своим полуприцепом легковой автомобиль:
Есть специальный термин – расчетный автомобиль, его тактико-технические показатели используются при разработке проектов трасс регионального значения. Такие параметры, например: размер и R min поворота должны быть идентичными у каждого класса автотранспорта.
Нормы европейского стандарта регламентируют следующие габариты для автотранспорта большегрузной категории во время движения на поворотах:
Например: для автопоезда типа А16, имеющего линейный размер до 16 метров, и аналогичного вида А20 с длиной до 20 м прописаны строгие ограничения, указанные в приведенной ниже таблице:
| Тип автомобиля | R min поворота, м | R min внешний, м | R min внутренний, м |
| А16 | 9,7 | 10,2 | 6,2 |
| А20 | 12,1 | 12,6 | 8,5 |
Типичными прототипами для расчетных автомобилей могут служить:
Автопоезда с двумя или тремя прицепами, имеющие длину больше 20 метров, используются всеми перевозчиками мира, поэтому при разработке макетов автотрасс нужно проводить дополнительное компьютерное моделирование такого специфического движения во время поворотов на пересечениях дорог или городских перекрестках.
Особенности маневрирования
Водители-дальнобойщики обладают специфической подготовкой: уверенно входят в повороты на трассе и во время перемещений по городу, при прохождении перекрестков, потому что движения отработаны до автоматизма на специальных дорожках автодрома, как показано на этом видео:
Такой термин, как радиус разворота фуры должен учитываться при разработке подъездных путей к складским помещениям и местам разгрузки крупнотоннажного автомобильного транспорта. А разворотная площадка для фуры должна соответствовать утвержденным стандартам, чтобы большегрузный автомобиль мог уверенно маневрировать на выделенной для этих целей территории.
Таблица ширины площадки для ТС (транспортных средств)
| Тип авто | Длина ТС в м | Ширина площадки, м |
| Камаз | 10 | 22 |
| Еврофура | 18 | 38 |
Для нормального выполнения маневрирования при движении ТС надо располагать на площадке разгрузки друг от друга на расстоянии 3–4 метра.
Радиус разворота еврофуры
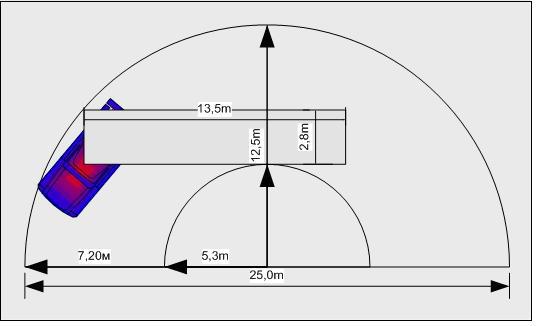
Европейские стандарты регламентируют ограничения по длине, например, для седельного автопоезда этот параметр – 16,5 метра. Размеры полуприцепа: 12 м от оси ССУ до кормовой части и 2,1 м до переднего бампера.
Стандартный радиус разворота еврофуры, например, на 180 или 360 градусов внутри воображаемой площади, которая составлена двумя окружностями с R = 12,5 м и 5,3 м, должен свободно выполняться при условии, что выступающие части машины не пересекают обозначенные границы во время маневрирования.
Радиус поворота «американца»
Тягачи с полуприцепами, разработанные американскими конструкторами, называют траками, а маневренность, особенно во время проезда по городу, ограниченная из-за большого линейного размера. Для поворота на 90 градусов такому крупногабаритному транспортному средству требуется в 2 раза больше радиуса, чем европейским аналогам. Поэтому иногда приходится видеть такие ситуации, как на фото.
Расчет радиуса по лекалам
При строительстве дорог во время осуществления проекта в компьютерном варианте используют специальные лекала, по которым скрупулезно выписывается кривизна каждого изгиба, особенно на развязке и пересечении с другими аналогами.
Как правило, лекала уже рассчитаны для всех типов автотранспортных средств. Такие данные можно скачать, например, по этой ссылке – https://dwg.ru/dnl/2627.
Прохождение поворотов
Умудренные опытом дальнобойщики чувствуют габариты автотранспортного средства, состоящего из тягача и полуприцепа с неуправляемой тележкой, а также возникающие сложности, связанные со смещением последней при вхождении в поворот.
Гораздо больше внимания водителю фуры требуется при выполнении маневрирования в черте города, где интенсивное движение пешеходов, а также легкового и общественного транспорта. Особо надо отметить сложности при проезде развязок и перекрестков – все необходимые маневры по изменению направления и смены полосы движения нужно выполнить заранее, но не ближе, чем за 20 метров от начала развязки или пересечения дорог.
Выполняя поворот направо, следует обратить внимание на встречную полосу дороги, т. к. автопоезд часто выезжает на нее, чтобы избежать заезда колесами тележки полуприцепа на бордюр, создавая угрозу травматизма пешеходов. При левом повороте не нужно стремиться проезжать центр перекрестка, потому что увеличивается площадь разворота, что затрудняет другому транспорту движение в нужную сторону.
Советы дальнобойщику
Управлять фурой так же трудно, как водить корабль по морю, здесь нужны навыки, многолетний опыт и профессионализм:
Важно! Сложным маневром считается постановка фуры на разгрузку. Не забывайте – полуприцепом руководят задние, а не передние колеса. Постоянно совершенствуйте профессиональные навыки, выполняя тренировочное маневрирование на специальных площадках.
Надеемся, что приведенные в статье рекомендации по прохождению сложных участков дороги помогут дальнобойщикам избежать нарушений ПДД. Помните, что опытный шофер видит далеко, а профессионал уверенно контролирует ситуацию вокруг управляемого транспортного средства.
Источник
Радиус поворота автомобиля: как измерить и можно ли изменить
Вопросы, рассмотренные в материале:
Выбирая новую машину, человек обращает внимание на ее главные параметры, например, сколько литров мотор, какова его мощность, автоматическая, роботизированная или механическая коробка передач и тому подобное. Но во время эксплуатации транспортного средства не менее важны и другие характеристики, такие как радиус поворота автомобиля. На что оказывает влияние данный параметр? Как его измерить? В нашей сегодняшней статье разбираемся в этом непростом понятии.
Что такое радиус поворота автомобиля
Название данного параметра говорит само за себя. Радиус поворота автомобиля — это полуокружность, описываемая машиной при совершении маневра, когда рулевое колесо полностью вывернуто.
Необходимо знать данное значение. Кроме того, следует видеть разницу между разворотом по малому и большому радиусу. Иногда в руководстве по эксплуатации указывается два параметра, которые разделены дробью.
Минимальный радиус поворота автомобиля — это след от наружного колеса, оставляемый машиной при совершении маневра. Еще этот параметр называют «от бордюра до бордюра». Но в этом показателе не учтены габариты переднего свеса, а от его длины зависит точность значения. В реальной жизни лучше всего пользоваться радиусом «от стены до стены». В нем учтены препятствия, которые включены в минимальное пространство по наружным размерам и которые может задеть бампер.
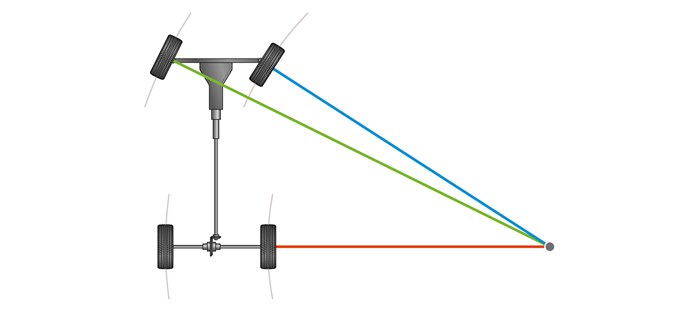
Однако сложности на этом не заканчиваются. Есть еще одна особенность, про которую необходимо помнить, когда вы совершаете маневр в стесненных обстоятельствах. Когда машина поворачивает, происходит смещение части кузова внутрь. Поэтому, если вы выезжаете со стоянки, не следует резко выворачивать рулевое колесо в крайнее положение. Так может произойти столкновение со стоящим рядом транспортным средством.
Как рассчитать радиус поворота автомобиля? Узнайте минимальный габаритный коридор для своего авто. Для этого придется определить расстояние, отделяющее наименьшую и наибольшую окружности. Обладая этой информацией, вы сможете выполнять сложные маневры в стесненных обстоятельствах, например на узком дорожном полотне, а также поворачивать, не нарушая правил дорожного движения.
Сегодня управлять машиной нелегко, ведь дороги загруженны, и места для маневров недостаточно. Например, если вы живете в большом городе и вам нужно припарковать автомобиль, то наверняка придется располагать машину вплотную к другим транспортным средствам и производить сложнейшие маневры.
Радиус поворота легкового автомобиля показывает, насколько машина маневренная, получится ли на ней поворачивать на узком дорожном полотне или когда пространство ограниченно.
Управление автомобилем даже в ограниченном пространстве окажется более комфортным, если данный показатель будет наименьшим. Когда вы знаете минимальный радиус поворота автомобиля, а также ширину дороги, то сможете рассчитать, можно ли за один раз выполнить маневр.
Автопроизводители всегда указывают радиус поворота для каждой машины. Чтобы узнать это значение, нужно изучить технические характеристики машины или инструкцию по эксплуатации Однако тут важно не ошибиться. Дело в том, что чаще всего указывается именно наименьший показатель, то есть разворот по малому радиусу. Делается это для того, чтобы машина в глазах покупателя выглядела маневреннее, чем это есть в реальности. Как определить настоящий радиус поворота легкового автомобиля? Для этого нужно учесть размеры свеса машины.
Как измерить радиус поворота автомобиля
Чтобы рассчитать радиус поворота автомобиля, можно использовать два способа: «от бордюра до бордюра» либо «от стены до стены».
В первом случае мы получим значение радиуса полуокружности, описываемой колесами машины, когда она разворачивается. Таким образом, для измерения необходимо сделать меловые отметки стартового положения внешнего колеса. После этого выворачиваем рулевое колесо до предела и совершаем поворот на 180°. Снова делаем меловую отметку конечной точки. Затем измеряем расстояние между отметками, делим получившиеся число на 2. С помощью данного способа можно узнать, какая минимальная ширина дорожного полотна должна быть, чтобы можно было совершить разворот.

Нельзя забывать про то, что у машины есть передний свес (промежуток от оси передних колес до конца переднего бампера). И когда дорожное полотно ограничивается бордюром с большой высотой, водитель не сможет совершить разворот, даже если уложится в радиус «от бордюра до бордюра». Произойдет следующее: машина упрется передним бампером в препятствие.
Поэтому, чтобы узнать настоящий показатель радиуса, придется измерять его по способу «от стены до стены». Как это делается? Мел закрепляют на стержне, который размещен на наружном углу бампера (по отношению к повороту). После этого водитель разворачивается и замеряет диаметр полученной полуокружности. Затем полученное число делится на 2.
Так как производители авто хотят, чтобы их творения выглядели наиболее маневренными, то в характеристиках и рекламных проспектах обычно указывают радиус поворота «от бордюра до бордюра». Ведь его значение меньше по сравнению с показателем «от стены до стены». На практике же, если вам нужно выбрать наиболее маневренный автомобиль, важно учесть также и длину переднего свеса.
Обратите внимание! Есть одна особенность, которая связана с радиусом поворота легкового автомобиля. На самом деле это понятие используется в разговорной речи. Потому что настоящий параметр, который отражает расстояние, требуемое для совершения маневра от упора до упора, — диаметр. Поэтому в габаритных и технических характеристиках обычно указан именно диаметр. Здесь важно не запутаться в этих понятиях.
Нередко даже автопроизводители допускают ошибки. Так, в пресс-релизе нового «Ленд Крузер Прадо» в «Тойота» отметили, что машина сохранила отличный диаметр разворота, который составляет только 5,8 метров. Но это нереально, потому что длина автомобиля 4, 84 метра.
Но если вы изучите рекламный проспект к этой машине, то там уже будет сказано «минимальный радиус разворота автомобиля по колесам», это уже соответствует действительности. Для подтверждения этого просто зайдите на официальный портал. Там отмечен именно диаметр, а не радиус поворота легкового автомобиля, который составляет 11,6 м.
Можно ли изменить радиус поворота автомобиля
Очевидно, что радиусы поворота грузовых автомобилей, седанов или кроссоверов определяются габаритами транспортного средства, а также углом поворота передних колес. Изменить размеры авто невозможно. При этом угол поворота колес на стоковой машине ограничивается параметрами функционирования руля. Если на авто передний привод, при этом рабочие диапазоны ШРУС, или «гранат», это значит, что выворачивать до упора колеса не стоит. Чтобы не запутаться в теории, запомните, что изменить радиус можно, но для этого придется менять конструкцию транспортного средства, а это ухудшит его работу.
Не боитесь потерять гарантию? Тогда радиус можно сделать меньше.
Насколько маневренность машины улучшится после вмешательства? Это определяется конструктивными особенностями авто. Однако чаще всего заметно улучшается запас хода руля, в результате радиус поворота автомобиля становится меньше.
Причем изменить этот параметр на некоторых моделях авто бывает достаточно просто, особенно если конструкция рулевого управления позволяет сделать это.

Пластиковые ограничители определяют то, каким будет запас хода рулевой рейки. Как сделать угол поворота колес больше? Для этого уменьшаем толщину распорок или же подпиливаем их (стачиваем). Также можно монтировать не оригинальные тонкие проставки из пластика.
К сожалению, после такого вмешательства колеса станут задевать подвеску и кузов авто. Что делать?
Можно воспользоваться тонкими пластиковыми ограничителями, которые вы сделаете своими руками. Потребуется заготовка с таким же диаметром, как у оригинального ограничителя хода рулевой рейки.
Не хотите, чтобы колеса во время маневров задевали подвеску и кузов? Тогда монтируйте проставки на ступицы для выноса колес. Так вы увеличите ширину между передними колесам. В результате радиус станет больше, при этом колеса не будут ничего задевать.
Влияет ли изменение угла кастора на радиус поворота автомобиля
Для примера возьмем автомобиль УАЗ Patriot, который имеет следующие характеристики:
Какой вид имеет формула влияния кастора на реальный угол поворота колеса:
a’ = tan-1((SIN(a) * COS(caster))/COS(a))
В ходе эксперимента найдем нужные показатели, построим 3D-модель, а затем измерим реальный угол пересечения плоскостей дороги и колеса.
В результате у нас получились нижеследующие параметры a’:
Воспользуемся формулой R = L tan(А), в которой:
А — угол поворота колеса.
Чтобы схему было проще понять, дополним ее:
R1 — минимальный радиус поворота автомобиля;
R2 — радиус пути заднего наружного колеса;
R3 — максимальный радиус поворота автомобиля;

Прямоугольный треугольник образуется передним внутренним колесом, задним внутренним колесом, а также точкой, вокруг которой машина разворачивается. В этом треугольнике:
угол А — угол поворота колеса;
катет а — колесная база (2760 мм) — L;
катет б — минимальный радиус поворота автомобиля — R1;
Как найти минимальный радиус R1:
R1 = L / tan(A) = 2760 / tan(26,968) =
R1 = L / tan(A) = 2760 / tan(26,774) =
Приступим к определению R2, то есть радиусу пути заднего внешнего колеса.
R2 = радиус внутреннего колеса + ширина колеи моста.
R2 = R1 + H = 5424 + 1600 = 7024 мм
R2 = R1 + H = 5470 + 1600 = 7070 мм
В завершение найдем R3, то есть максимальный радиус поворота автомобиля.
В нашем примере прямоугольный треугольник описан передним внешним и задним внешним колесом, а также точкой, вокруг которой машина разворачивается.
Что получится здесь:
Катет а = L(колесная база) = 2760 мм
Катет б = R2 = радиус пути заднего внешнего колеса
Гипотенуза = R3, то есть максимальный радиус поворота автомобиля.
Теорема Пифагора определяет соотношение между сторонами прямоугольного треугольника, в котором сумма квадратов длин катетов равняется квадрату длины гипотенузы.
R3 = SQRT(2760^2 + 7024^2) =
R3 = SQRT(2760^2 + 7070^2) =
Конечно, полученные показатели немного не соответствуют радиусу поворота автомобиля УАЗ Patriot, которые содержатся в руководстве (6,5 м против 7,5 м). Это объясняется погрешностями в методике расчета, а также исходных данных. Однако если рассчитать среднее значение между минимальным и максимальным радиусом (5,5 м и 7,5 м соответственно), в результате у нас будет 6,5 м.
Так или иначе, но можно прийти к выводу, что кастор влияет на радиус. То есть для нас важнее не абсолютные значения, но их относительная разница. В нашем примере она составит:
R3(для кастора +8°) — R3(для кастора +3°) = 7589 — 7546 = 43 мм, то есть меньше чем 5 см
При этом если будет отклонение ограничения поворота колеса на 1°, то это повлияет в 5 раз сильнее на радиус поворота по сравнению с отклонением кастора на 1°.
Что автомобилисты говорят про радиус поворота автомобиля
«Чтобы сделать радиус меньше, ограничительные болты выставляю на глаз, после того как установил новые ШОПКи. Главное, чтобы они не соприкасались с кулаками».
«Помимо Volvo, еще у Lexus поперечное расположение силового агрегата. Но здесь и габариты, а также база отличаются. На других машинах мотор расположен продольно. Поперечное расположение приводит к тому, что коробка передач и трансмиссия размещаются определенным образом. В результате вывернуть колеса сильнее просто не получится».
«Раньше немецкие производители поставляли автобусы MAN, у которых были 2 соединенных полуприцепа длиной 23 метра. Такой автобус во время маневров мог достать себя за хвост 1 м, ездил змейкой, при этом мосты шли по одной колее. Ни разу не был за рулем такого авто, но несколько раз наблюдал».
«Каждый водитель должен знать радиус поворота автомобиля. Я вот, например, спустя 3 часа после покупки поцарапал новенькую машину при развороте. Но с опытом стал аккуратнее».
«Я не переживаю во время разворотов. Потому что даже если ты делаешь его медленно, другие участники дорожного движения все равно подождут. А вот умение поворачивать на большие углы в ограниченном пространстве это действительно важно.
Например, в самом центре мегаполиса, где улочки узкие, а парковки забиты, необходимо уметь поворачивать на 90, когда ширина свободной проезжей части на дороге практически равна ширине машины. Или, например, если вам надо выехать с парковки, на которой автомобили прижаты друг к другу, а противоположный ряд слишком близко. Да существует множество ситуаций, когда небольшой радиус просто необходим».
Источник
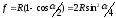
![inj_geo_2-129.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-129.jpg)
![inj_geo_2-130.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-130.jpg)