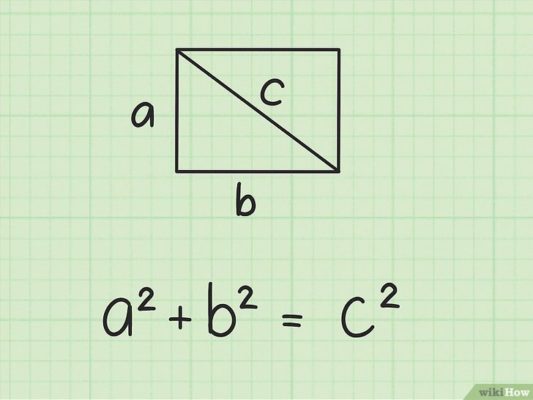Как находить длину
Длиной принято обозначать расстояние между двумя точками какого-либо отрезка. Это может быть прямая, ломаная или замкнутая линия. Вычислить длину можно довольно простым путем, если знать некоторые другие показатели отрезка.

Инструкция
Если вам нужно найти длину стороны квадрата, то это не составит труда, если вам известна его площадь S. В связи с тем, что все стороны квадрата имеют одинаковую длину, вычислить величину одной из них можно по формуле: a = √S.
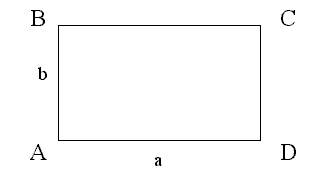
В случае, когда требуется просчитать длину стороны прямоугольника, воспользуйтесь значениями его площади s и длины другой стороны b. Из формулы a=S/b вы получите искомое значение.
Чтобы определить длину окружности, то есть замкнутой линии, которая образует круг, воспользуйтесь значениями: r – ее радиусом и D – диаметром. Диаметр можно вычислить, умножив радиус окружности на 2. Известные вам значения подставьте в формулу определения длины окружности: C=2πr=πD, где π=3,14.
Для вычисления длины обычного отрезка воспользуйтесь методом эксперимента. То есть возьмите линейку и измеряйте.
Для того чтобы вычислить длину стороны такой фигуры, как треугольник, вам понадобятся размеры двух других сторон, а также величины углов. Если вы имеете дело с прямоугольным треугольником, и один из его углов равен 60 градусам, то величину его катета можно определить по формуле a=c*cosα, где c – гипотенуза треугольника, а α – угол между гипотенузой и катетом.
Помимо этого, если вы располагаете такими известными величинами, как высота b и площадь S треугольника, то длину стороны, которая является основанием, можно узнать благодаря формуле a=2√S/√√b.
Что касается правильного многоугольника, то длину его стороны можно просчитать, руководствуясь формулой an=2R*sin(α/2)=2r*tg(α/2), где R – радиус описанной окружности, r – радиус вписанной окружности, n – количество углов.
Если вы хотите вычислить длину равносторонней фигуры, вокруг которой описана окружность, то сделать это можно по формуле an=R√3, где R – радиус окружности, n – количество углов фигуры.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Обновлено: 20.05.2023
Величина — это то, что можно измерить. Такие понятия, как длина, площадь, объём, масса, время, скорость и т. д. называют величинами. Величина является результатом измерения, она определяется числом, выраженным в определённых единицах. Единицы, в которых измеряется величина, называют единицами измерения.
Для обозначения величины пишут число, а рядом название единицы, в которой она измерялась. Например, 5 см, 10 кг, 12 км, 5 мин. Каждая величина имеет бесчисленное множество значений, например длина может быть равна: 1 см, 2 см, 3 см и т. д.
Одна и та же величина может быть выражена в разных единицах, например килограмм, грамм и тонна — это единицы измерения веса. Одна и та же величина в разных единицах выражается разными числами. Например:
5 см = 50 мм (длина),
1 ч = 60 мин (время),
2 кг = 2000 г (вес).
Измерить величину — значит узнать, сколько раз в ней содержится другая величина того же рода, принятая за единицу измерения.
Например, мы хотим узнать точную длину какой-нибудь комнаты. Значит нам нужно измерить эту длину при помощи другой длины, которая нам хорошо известна, например при помощи метра. Для этого откладываем метр по длине комнаты столько раз, сколько можно. Если он уложится по длине комнаты ровно 7 раз, то длина её равна 7 метрам.
В результате измерения величины получается или именованное число, например 12 метров, или несколько именованных чисел, например 5 метров 7 сантиметров, совокупность которых называется составным именованным числом.
В каждом государстве правительство установило определённые единицы измерения для различных величин. Точно рассчитанная единица измерения, принятая в качестве образца, называется эталоном или образцовой единицей. Сделаны образцовые единицы метра, килограмма, сантиметра и т. п., по которым изготавливают единицы для обиходного употребления. Единицы, вошедшие в употребление и утверждённые государством, называются мерами.
Меры называются однородными, если они служат для измерения величин одного рода. Так, грамм и килограмм — меры однородные, так как они служат для измерения веса.
Единицы измерения
Ниже представлены единицы измерения различных величин, которые часто встречаются в задачах по математике:
Меры веса/массы:
- 1 тонна = 10 центнеров;
- 1 центнер = 100 килограмм;
- 1 килограмм = 1000 грамм;
- 1 грамм = 1000 миллиграмм.
Меры длины:
- 1 километр = 1000 метров;
- 1 метр = 10 дециметров;
- 1 дециметр = 10 сантиметров;
- 1 сантиметр = 10 миллиметров.
Меры площади (квадратные меры):
- 1 кв. километр = 100 гектарам;
- 1 гектар = 10000 кв. метрам;
- 1 кв. метр = 10000 кв. сантиметров;
- 1 кв. сантиметр = 100 кв. миллиметрам.
Меры объёма (кубические меры):
- 1 куб. метр = 1000 куб. дециметров;
- 1 куб. дециметр = 1000 куб. сантиметров;
- 1 куб. сантиметр = 1000 куб. миллиметров.
Рассмотрим ещё такую величину как литр. Для измерения вместимости сосудов употребляется литр. Литр является объёмом, который равен одному кубическому дециметру (1 литр = 1 куб. дециметру).
Меры времени:
- 1 век (столетие) = 100 годам;
- 1 год = 12 месяцам;
- 1 месяц = 30 суткам;
- 1 неделя = 7 суткам;
- 1 сутки = 24 часам;
- 1 час = 60 минутам;
- 1 минута = 60 секундам;
- 1 секунда = 1000 миллисекундам.
Кроме того, используют такие единицы измерения времени, как квартал и декада.
Месяц принимается за 30 дней, если не требуется определить число и название месяца. Январь, март, май, июль, август, октябрь и декабрь — 31 день. Февраль в простом году — 28 дней, февраль в високосном году — 29 дней. Апрель, июнь, сентябрь, ноябрь — 30 дней.
Год представляет собой (приблизительно) то время, в течении которого Земля совершает полный оборот вокруг Солнца. Принято считать каждые три последовательных года по 365 дней, а следующий за ними четвёртый — в 366 дней. Год, содержащий в себе 366 дней, называется високосным, а годы, содержащие по 365 дней — простыми. К четвёртому году добавляют один лишний день по следующей причине. Время обращения Земли вокруг Солнца содержит в себе не ровно 365 суток, а 365 суток и 6 часов (приблизительно). Таким образом, простой год короче истинного года на 6 часов, а 4 простых года короче 4 истинных годов на 24 часа, т. е. на одни сутки. Поэтому к каждому четвёртому году добавляют одни сутки (29 февраля).
Об остальных видах величин вы узнаете по мере дальнейшего изучения различных наук.
Сокращённые наименования мер
Сокращённые наименования мер принято записывать без точки:
Измерительные приборы
Для измерения различных величин используются специальные измерительные приборы. Одни из них очень просты и предназначены для простых измерений. К таким приборам можно отнести измерительную линейку, рулетку, измерительный цилиндр и др. Другие измерительные приборы более сложные. К таким приборам можно отнести секундомеры, термометры, электронные весы и др.
Измерительные приборы, как правило, имеют измерительную шкалу (или кратко шкалу). Это значит, что на приборе нанесены штриховые деления, и рядом с каждым штриховым делением написано соответствующее значение величины. Расстояние между двумя штрихами, возле которых написано значение величины, может быть дополнительно разделено ещё на несколько более малых делений, эти деления чаще всего не обозначены числами.
Определить, какому значению величины соответствует каждое самое малое деление, не трудно. Так, например, на рисунке ниже изображена измерительная линейка:
Цифрами 1, 2, 3, 4 и т. д. обозначены расстояния между штрихами, которые разделены на 10 одинаковых делений. Следовательно, каждое деление (расстояние между ближайшими штрихами) соответствует 1 мм. Эта величина называется ценой деления шкалы измерительного прибора.
Перед тем как приступить к измерению величины, следует определить цену деления шкалы используемого прибора.
Для того чтобы определить цену деления, необходимо:
- Найти два ближайших штриха шкалы, возле которых написаны значения величины.
- Вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.
В качестве примера определим цену деления шкалы термометра, изображённого на рисунке слева.
Возьмём два штриха, около которых нанесены числовые значения измеряемой величины (температуры).
Например, штрихи с обозначениями 20 °С и 30 °С. Расстояние между этими штрихами разделено на 10 делений. Таким образом, цена каждого деления будет равна:
(30 °С – 20 °С) : 10 = 1 °С
Следовательно, термометр показывает 47 °С.
Измерять различные величины в повседневной жизни приходится постоянно каждому из нас. Например, чтобы прийти вовремя в школу или на работу, приходится измерять время, которое будет потрачено на дорогу. Метеорологи для предсказания погоды измеряют температуру, атмосферное давление, скорость ветра и т. д.
Размерность длины — dim l = L. В ряду других пространственных величин длина — это величина единичной размерности, тогда как площадь — двухмерная, объём — трёхмерная. В большинстве систем измерений единица длины — одна из фундаментальных единиц измерения, на основе которых образуются другие единицы. В международной системе единиц (СИ) за единицу длины принят метр.
Содержание
Единицы измерения длины
Метрическая система
Метрическая система считается самой удобной из всех придуманных из-за своей простоты. В основе метрической системы лежит единица измерения метр. Все остальные единицы измерения являются кратными степеням десяти от метра (например, километр — это 10³ метров и т. п.), что позволяет облегчить подсчёты. До 1960 года у метра был специальный эталон, ныне хранящийся в Париже. Сегодня, по определению, метр равен расстоянию, которое проходит свет в вакууме за 1/299 792 458 долю секунды.
Британская/Американская система
Исходными английскими мерами длины были миля, ярд, фут и дюйм. Миля пришла в Англию из Древнего Рима, где она определялась как тысяча двойных шагов вооружённого римского воина.
Старорусская система
В Древней Руси мерой длины, веса и т. п. являлся человек. На это указывают названия мер длины: локоть (расстояние от конца вытянутого среднего пальца руки или сжатого кулака до локтевого сгиба), пядь (расстояние между вытянутым большим и указательным пальцами руки), сажень (расстояние от конца пальцев одной руки до конца пальцев другой) и другие [1] .
См. также
Древнегреческая система
Мусульманская система
- Ангушт или Асба (аналог дюйма)
- Пай (аналог фута)
- Ба или кама, равная приблизительно 2 м
- Касаба или наб
- Фарсах или парасанг, равный трём милям по 1000 Ба, или 6 км
- Барид, равный четырём фарсахам [3]
Типографическая система
Морская система
Морская система измерения длины привязана к размеру планеты Земля. В качестве основной единицы измерения принята морская миля, равная длине одной минуты (1/60 градуса) дуги меридиана земного эллипсоида. Длина морской мили является величиной переменной, зависящей от широты. Ее численное значение составляет от 1843 метров на экваторе до 1861,6 метров на полюсах.
Международная морская миля составляет 1852 м, в отличие от морской мили Британской системы (1853,184 м). Для измерения меньших размеров применяют кабельтов — 1/10 морской мили, или 185,2 м (округлённо — 185 м). [4]
Единицы, применяемые в астрономии
Средства измерений длины, расстояния
Измерительные инструменты и меры
Измерительные приборы
Другие средства
- Большие расстояния в навигации определяются при помощи средств радионавигационных систем или спутниковых систем
- Очень маленькие расстояния измеряются с помощью измерительных микроскопов
См. также
Примечания
- ↑Меры длины
- ↑Отечественные компании переходят на исторические меры длины
- ↑Власов А.Д., Мурин Б.П. Единицы физических величин в науке и технике: Справочник. — М .: Энергоатомиздат, 1990. — С. 176. — ISBN 5-283-03966-8
- ↑Учебник по навигации
- Физические величины по алфавиту
- Метрология
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое “Длина” в других словарях:
длина — ы; ж. 1. Протяжение чего л.; расстояние между кем , чем л. Меры длины. Измерить длину и ширину. Д. отрезка прямой. Д. пути. Д. судоходного канала. Во всю длину. Длиною в три метра. 2. Продолжительность, длительность (о времени). Д. рабочего дня.… … Энциклопедический словарь
ДЛИНА — ДЛИНА, длины, мн. нет, жен. Протяжение линии, плоскости, тела в том направлении, в котором две крайние точки (линии, плоскости, тела) лежат на наибольшем расстоянии одна от другой. Предметы измеряются в длину, ширину и высоту. Длина стола. Меры… … Толковый словарь Ушакова
ДЛИНА — жен. протяжение вдоль, долина; пск. долица, должина, твер., пск. длинь, пермяц. доль; за длину пространства, тела или вещи обычно берется направление наибольшего протяжения его; длина, ширина и вышина, или мера по уровню вдоль и поперек и мера по … Толковый словарь Даля
длина — сущ., ж., употр. сравн. часто Морфология: (нет) чего? длины, чему? длине, (вижу) что? длину, чем? длиной, о чём? о длине; мн. что? длины, (нет) чего? длин, чему? длинам, (вижу) что? длины, чем? длинами, о чём? о длинах 1. Длиной предмета является … Толковый словарь Дмитриева
ДЛИНА — 1) Длина отрезка прямой расстояние между его концами.2) Длина ломаной сумма длин ее звеньев.3) Длина дуги кривой предел длины вписанной в нее ломаной, когда число ее звеньев неограниченно возрастает, причем длина каждого звена стремится к нулю … Большой Энциклопедический словарь
длина — продолжительность, протяжённость, расстояние, длительность, долгота; периметр, метраж, пикет, протяжение, апофема, протяженность Словарь русских синонимов. длина 1. протяжённость, протяжение 2. см. длительность … Словарь синонимов
длина — ДЛИНА1, ы, ж Протяженность предмета, расстояние между двумя крайними точками его, расположенными на одной линии или одной плоскости и находящимися на наибольшем (в отличие от ширины) отдалении друг от друга. Павел увеличил длину брюк в… … Толковый словарь русских существительных
длина — из *дьлина, ср. др. русск. д(ь)ля длина (напр., в Хож. игум. Дан. 18). От длить; ср. укр. длити, ст. слав. продьлити μηκύνειν, чеш. dlim, dliti. Родственно праслав. *dьlgъ (см. долгий); ср. Бернекер 1, 252 и сл.; Траутман, BSW 55; Mi. EW 55.… … Этимологический словарь русского языка Макса Фасмера
ДЛИНА — ДЛИНА, ы, мн. (спец.) длины, длин, длинам, жен. Величина, протяжённость чего н. в том направлении, в к ром две крайние точки линии, плоскости, тела лежат, в отличие от ширины, на наибольшем расстоянии друг от друга. Измерить стол в длину и в… … Толковый словарь Ожегова
– числовая характеристика протяженности линий в метрич. пространстве. Д. отрезка прямой – расстояние между его концами, измеренное каким-либо отрезком, принятым за единицу Д. Длина ломаной – сумма Д. ее звеньев. Д. простой дуги – точная верхняя грань длин
ломаных, вписанных в эту дугу. Всякая непрерывная кривая имеет Д.- конечную или бесконечную. Если ее Д. конечна, то кривая наз. спрямляемой. Д. плоской кривой, заданной в прямоугольных координатах уравнением y=f(x), а (f(x)имеет непрерывную производную f’(x)), выражается интегралом
Если кривая задана в параметрич.форме
то Д. кривой равна
Д. спрямляемой кривой не зависит от параметризации. Д. пространственной кривой, заданной в параметрич. форме x=x(t), y=y(t), z=z(t), выражается формулой
в случае re-мерного пространства
Пусть у- непрерывно дифференцируемая кривая, заданная функциями u=u(t), v=v(t), на непрерывно дифференцируемой поверхности r= r( и, v). Тогда длина дуги кривой от точки, соответствующей значению параметра t= t0, равна
где I – первая квадратичная форма поверхности. Д. непрерывно дифференцируемой кривой, заданной функциями х i =х i ( t),в римановом пространстве с метрич. тензором gik, равна
апофема, длительность, долгота, метраж, периметр, пикет, продолжительность, протяжение, протяженность
Смотреть что такое ДЛИНА в других словарях:
ДЛИНА
числовая характеристика протяжённости линий. В разных случаях понятие Д. определяется различно. 1) Д. отрезка прямой — расстояние между его кон. смотреть
ДЛИНА
ДЛИНА, -ы, мн. (спец.) длины, длин, длинам, ж. Величина, протяженностьчего-н. в том направлении, в к-ром две крайние точки линии, плоскости, телалежат, в отличие от ширины, на наибольшем расстоянии друг от друга. Измеритьстол в длину и в ширину, меры длины. Д. улицы. Д. дуги. Д. реки. Д.радиоволны. смотреть
ДЛИНА
длина ж. 1) а) Протяжение линии, плоскости, тела и т.п. в том направлении, в котором две крайние его точки наиболее удалены друг от друга. б) Протяженность, расстояние между концами чего-л. 2) Продолжительность, длительность (о времени).
ДЛИНА
длина ж. тк. ед.length в длину — lengthwise, longwise во всю длину — at full length; (рд.) the full length (of); all along (smth.) растянуться во всю д. смотреть
ДЛИНА
длина продолжительность, протяжённость, расстояние, длительность, долгота; периметр, метраж, пикет, протяжение, апофема, протяженность Словарь русских синонимов. длина 1. протяжённость, протяжение 2. см. длительность Словарь синонимов русского языка. Практический справочник. — М.: Русский язык.З. Е. Александрова.2011. длина сущ., кол-во синонимов: 10 • апофема (3) • длительность (11) • долгота (5) • метраж (3) • периметр (2) • пикет (10) • продолжительность (14) • протяжение (10) • протяженность (11) • размер (43) Словарь синонимов ASIS.В.Н. Тришин.2013. . Синонимы: апофема, длительность, долгота, метраж, периметр, пикет, продолжительность, протяжение, протяженность Антонимы: краткость, размах, широта. смотреть
ДЛИНА
ДЛИНА, числовая характеристика протяжённости линий. В разных случаях понятие Д. определяется различно. 1) Д. отрезка прямой – расстояние между его ко. смотреть
ДЛИНА
length, run, stretch* * *длина́ ж.lengthв длину́ — endways, endwise, lengthwiseво всю длину́ — the full lengthна едини́цу длины́ — per unit (of) len. смотреть
ДЛИНА
1) length2) patn– длина анкеровки– длина базиса– длина базы– длина вектора– длина взаимодействия– длина волновая– длина волны– длина выбега– длина дуги. смотреть
ДЛИНА
ж.length- акустическая длина пути- апертурная длина- базовая длина- бесконечная длина- геометрическая длина пути- геометрическая длина- гравитационная . смотреть
ДЛИНА
– числовая характеристика протяженности линий в метрич. пространстве. Д. отрезка прямой – расстояние между его концами, измеренное каким-либо отрез. смотреть
ДЛИНА
ДЛИНА ж. протяжение вдоль, долина; пск. долица, должина, твер. пск. длинь, перм. доль; за длину пространства, тела или вещи обычно берется направление наибольшего протяжения его; длина, ширина и вышина, или мера по уровню вдоль и поперек и мера по отвесу, составляют три основные протяжения всякого тела или пространства. Длина градуса, мера его погонною мерой, верстами, саженями и пр. В длину, длиною, долиню три сажена. Эка длина какая! Длинный, большой длины, в пространстве или во времени; долгий. Весенний день длинен (долог), да нитка коротка: а осенний день короток, да нитка длинна (долга). Народ более любит слово долгий, а мы относим его почти только ко времени. Волос долог, а язык длинней (у бабы). Это еще длинна (долга) песня. Длинненький, длинноватый, длиннёхо(ше)нек. длинным-длиннешенек. Длинник м. мера или протяжение в длину, длина. Лесок потянулся длинником. В десятине длиннику 80, поперечнику 30 сажен. | Брус, доска; связь или настилка в длину, вдоль; противопол. поперечник; продольное бревно, брус, жердь. | Стар. батог, палка, хлыст. прут, которым наказывали. | Орл. вор. узкая полоса земли, пай или участок, поле. | Астрах. четырехсаженное бревно. | У астрах. рыбаков, длинник самоловная снасть: к веревке (хребтине) привязывают на поводцах 50 удочек, без наживы; рыба, проходя, садится боком; два длинника составляют счал, а три длинника – перетягу: сотня и более перетяг, до 20 тыс. крючков, занимают около версты и назыв. порядком. Ставить длинники в море на чипчиках кольях), назыв. выбивать порядки. Длинник м. вологодск. узкая и долгая полоса пашни. Длинняк м. собират. жердняк, шесты, жерди, слеги. Длиннота ж. длина, длинь, как свойство, состояние; более о времени, о растянутом разсказе и пр. Длинноватость ж. состояние, качество того, что длинновато, немного или чересчур длинно. Длинногривый, длнно(долго)ногий, длинноносый, длиннополый, длиннотенный, длинношерстый и пр. понятны по составу; говорят также: долгогривый, долгополый и пр. Длинноголенка, растен. Macrocnemum голенастка, переводн. Длинноголовка, растен. Erycbbe головчатка, переводн. Длинноколенка, растен. Phalangium, перeводн. коленчатка. Длиннососудка, растен. Mecardonia. Длинностручник растен. Macrolobium, переводн. Длиннотычинник, растен. Macrostemma Длинноцветник, растен. Selena. Названия эти придуманные, переводные. Длить, тянуть время, мешкать, медлить, откладывать, оттягивать, пробавляться. Он попусту длит делом, он только время длит. Длиться тянуться, продолжаться; | казаться долгим, противопол. коротаться. Болезнь длится более года. С немилым часы длятся. Длительный, продолжительный, долгий, медленный, мешкотный, медлительный. Длительность ж. свойство, состояние длительного; медленность. Длитель м. -ница ж. кто медлит, тянет время: медлитель, мешкатель.
ДЛИНА
ДЛИНА́, ы́, ж.1.Размер, мера чего-л. в направлении наибольшего протяжения.Объявить .. длину, вышину, ширину двор, в котором дѣло дѣлатись имѣет. ДМТ 86. смотреть
Длина́ — физическая величина, числовая характеристика протяжённости линий.
В большинстве систем измерений единица длины — одна из основных единиц измерения, через которые определяются другие (производные) единицы. В международной системе единиц (СИ) за единицу длины принят метр.
В узком смысле под длиной понимают линейный размер предмета в продольном направлении(это направление наибольшего размера), то есть расстояние между его двумя наиболее удалёнными точками, измеренное горизонтально, в отличие от высоты, которая измеряется в вертикальном направлении, а также ширины или толщины, которые измеряются поперёк объекта (под прямым углом к длине).
1. Протяжение линии, плоскости, тела в том направлении, в котором две крайние его точки наиболее удалены друг от друга. Меры длины. Измерить длину и ширину. || Расстояние между концами чего-л.; протяжение, протяженность. Длина отрезка прямой. Длина пути. Длина судоходного канала. □ Веревка была длиною почти во всю комнату. Пушкин, Дубровский. На окраине [города], по всей длине улицы, остановилась на ночь колонна грузовых машин. Первенцев, Огненная земля.
2. Продолжительность, длительность. Длина рабочего дня. Длина рассказа.
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
- Длина — физическая величина, числовая характеристика протяжённости линий. В узком смысле под длиной понимают линейный размер предмета в продольном направлении (обычно это направление наибольшего размера), то есть расстояние между его двумя наиболее удалёнными точками, измеренное горизонтально, в отличие от высоты, которая измеряется в вертикальном направлении, а также ширины или толщины, которые измеряются поперёк объекта (под прямым углом к длине).
от англ. length (длина).
ДЛИНА’, ы́, мн. нет, ж. Протяжение линии, плоскости, тела в том направлении, в к-ром две крайние точки (линии, плоскости, тела) лежат на наибольшем расстоянии одна от другой. Предметы измеряются в длину, ширину и высоту. Д. стола. Меры длины (совокупность принятых единиц линейного измерения). || Протяжение пути вдоль чего-н. Д. окружности. Д. реки. Д. дороги. || перен. Длительность, величина. Д. романа.
длина́
Читайте также:
- Чем опасны перерывы в электроснабжении предприятий кратко
- Как сделать школьные принадлежности для басика
- То чего не было гаршин краткое содержание
- Чем отличаются природные комплексы друг от друга кратко
- Какие принципы национальной политики провозгласила новая власть кратко
Длина прямоугольника

4.6
Средняя оценка: 4.6
Всего получено оценок: 89.
4.6
Средняя оценка: 4.6
Всего получено оценок: 89.
В этой статье мы поговорим о длине прямоугольника. Как определить, какая из сторон является длиной и зачем их разделять. Разберем три способа нахождения длины прямоугольника и решим небольшую задачу.
Опыт работы учителем математики – более 33 лет.
Что такое длина прямоугольника
Довольно часто люди путают местами длину и ширину прямоугольника, как правило, это не критично, но в результате значительно уменьшается наглядность, а от этого страдает качество решения.
Прямоугольник это частный случай параллелограмма. Параллелограмм, каждый угол которого равен 90 градусам, называется прямоугольником. Для наглядного изображения лучше будет, если нижней опорой прямоугольника будет служить длина. Так сложилось, что такой рисунок больше всего напоминает рисунки в учебнике, а потому ученику будет проще разобраться в теме.
Три способа найти длину прямоугольника
Если разделить фигуру на две части диагональю, то можно заметить, что прямоугольник поделится ею на два прямоугольных треугольника. Из этого разделения и вытекают все формулы длины прямоугольника.
-
Через теорему Пифагора
Если известна длина диагонали (обозначим ее буквой d) и длина прямоугольника (примем значение за букву a). Тогда корень квадратный из разности квадратов диагонали и длины будет равен ширине прямоугольника.
Чтобы было понятнее, напишем решение в виде нескольких формул.
Согласно теореме Пифагора – квадрат гипотенузы равен сумме квадратов катетов. Гипотенуза – это сторона, противоположная прямому углу, две другие стороны зовутся катетами. В нашем случае гипотенуза это диагональ.
Значит: d2=a2+b2 . Из этого выражения выразим квадрат ширины (значение «b»):b2=d2-a2
Для того, чтобы определить значение b, нужно взять корень квадратный из обеих сторон получившегося выражения: b=(d2-a2)(-1)
В случае необходимости, можно поменять местами а и b, тогда получится формула длины.
-
Через площадь
Рассмотрим еще один способ найти длину прямоугольника – через площадь.Площадь прямоугольника равна произведению длины и ширины. То есть, используя уже знакомые обозначения S=a*b. Выразим из этой формулы значение ширины: b=S/b.
Так же, как и в первом методе, можно поменять местами а и b, чтобы получить формулу для длины: a=S/b.
-
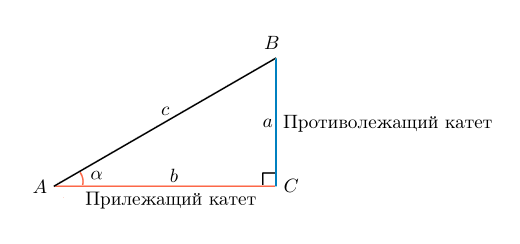
Тригонометрическая функция
Один из самых быстрых, но при этом немного сложных способов нахождения длины – воспользоваться тригонометрической функцией.
Если имеется прямоугольный треугольник, то соответственно имеются отношения, известные как синус и косинус.
Выберем угол между длиной и диагональю. Обозначим его α. Тогда sin α равен отношению катета, противоположного углу α к гипотенузе: Sin α = a/c
Значение синуса любого угла можно найти в таблицах Брадиса или с помощью калькулятора. Для удобства можно воспользоваться онлайн-версией, которая найдет значение отношения автоматически.
Но в формуле нет значения b, которое соответствует длине, а, значит, воспользуемся основным тригонометрическим тождеством. Косинус – это отношение стороны, прилежащей к углу, к гипотенузе: cos a=b/c
Значит можно найти длину, умножив косинус на гипотенузу: b=cos α*c
Задача
- Найти длину прямоугольника, если известно, что его ширина равна 3, а диагональ 5.
Воспользуемся теоремой Пифагора и найдем b. Длина равна корню квадратному из разности квадрата диагонали и квадрата ширины.
5^2=25
3^2=9
25-9=16
Корень квадратный из 16 равен 4.
Значение b=4
Что мы узнали?
Мы рассмотрели, как правильно изображать прямоугольник для большей наглядности, рассмотрели как можно найти длину или ширину при различных условиях задачи и решили задачу средней сложности на нахождение длины прямоугольника через теорему Пифагора.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 89.
А какая ваша оценка?
Статья «Длина отрезка и её измерение»
Составитель:
Новоселова Любовь Сергеевна
Не имели наши предки
Ни линейки, ни рулетки.
Но могли предмет любой
Измерять самим собой.
Ткани мерили локтями,
Землю мерили лаптями,
И имели пальцев пять –
Щели в доме измерять.
В общем, жили не тужили,
Не хлебали лаптем щей…
И всему на свете были
Люди – мерою вещей!
Ребята,
вам нужно измерить длину отрезка. Что вы возьмёте? (линейку) Представьте себе,
что были времена, когда человек не знал такого приспособления.
При
раскопке в древней Помпеи, был обнаружен измерительный инструмент, что
напоминал линейку. Она представляла собой тщательно отструганную дощечку,
которая помогала архитекторам в планировании сооружений. Линейка,
которой мы сейчас пользуемся, появилась во Франции. В 1812 такие линейки попали
в Россию как военный трофей, но их производство в нашей стране было налажено
лишь с 1999 года.
Единицы
измерения длины в Древней Руси
Понятие
“длина” появляется только тогда, когда требуется что-то измерить. Вот почему в
разные времена у разных народов мира существовали свои меры длины. И вот,
почему первые измерения расстояний были не точными, а приблизительными.
Что
необходимо было измерять людям в глубокой древности? Самые значительные
расстояния были те, которые приходилось преодолевать племени в поисках пищи.
Эти расстояния, как правило, измерялись несколькими днями пути. Например,
до озера три дня пути, дальние горы находятся на расстоянии 10 дней пути и т.д.
И первым помощником в определении таких больших расстояний выступала сама
природа: смена дня и ночи.
Близкие
расстояния древние люди измеряли полетом стрелы или копья. Такой идее людей
научила охота: зверь находится на расстоянии двух полетов стрелы, значит,
надо подойти поближе. И, конечно же, можно измерять небольшие расстояния
шагами. Надо было только научиться называть количество шагов. Но это как раз и
было самым трудным — сначала надо было научиться считать. Небольшие расстояния
мы и в настоящее время нередко определяем шагами.
Мерили
локтем, ступнями, пальцами, ногтями. Система древнерусских мер длины включала в
себя следующие основные меры: версту, сажень, локоть и пядь. Значение древнерусского локтя 10.25-10.5
вершков (в среднем приблизительно 46-47 см). Локоть широко применяли в торговле
как особенно удобную меру.
Первое
упоминание сажени встречается в старинных памятниках 1017 года и приписывается
киевскому монаху Нестору (“летописцу”). Сажень, представлявшая
наиболее крупную овеществленную единицу длины (существовали мерные веревки,
длина которых была равна сажени) получила широкое применение преимущественно
при измерении расстояний и в строительстве.
В
более поздние времена установилась мера расстояний верста.
Она
содержала в себе 750 сажень. Другое название версты — “поприще”.1
верста = 1,52 * 750 = 1140 метров.
У
наших предков слово “пядь” означало кисть руки. Первоначально под
пядью понималась мера длины, равная максимальному расстоянию по прямой между
концами вытянутых большого и указательного пальцев. Древнерусская система мер
длины имела следующий вид: 1 верста = 750 саженей = 2250 локтей = 4500 пядей. Разновидности
пяди: “малая пядь” — расстояние между концами вытянутых большого и
указательного пальцев (19 см); “пядь великая” — расстояние по прямой
между вытянутыми большим пальцем и мизинцем руки (20-25 см); “пядь с
кувырком” — длина малой пяди плюс 2 или 3 сустава указательного пальца (27
см).
В
XV-XVII вв. появились новые меры длины — аршин, с течением времени вытеснивший
локоть, и вершок. Название аршин
производится от персидского слова “арш”– “локоть”.
Вершок.
Наименование происходит от слова “верх” (“верх перста”,
т.е. пальца). Вершок упоминается в “Торговой книге” как 1/16 аршина.
В литературе XVII в. встречаются и доли вершка “полвершки” и
“четвертьвершки”.
|
|
Значение |
|
|
в русских мерах |
в метрических мерах |
|
|
Верста |
100 саженей |
2,16 км |
|
50 саженей |
1,08 км |
|
|
Сажень |
3 аршина |
2,16 м |
|
Аршин |
4 четверти |
72 см |
|
Локоть |
10 2/3 вершка |
48 см |
|
Четверть аршина |
4 вершка |
18 см |
|
Вершок |
— |
4,5 см |
Система
мер длины у Л.Ф. Магницкого имеет следующий вид:
·
1 сажень = 2 полусаженям = 3 аршинам,
·
1 аршин = 2 полуаршинам,
·
1 полуаршин = 2 четвертям,
·
1 четверть = 4 вершкам.
Это интересно
|
ЛОКОТЬ Локоть – исконно древнерусская мера длины, известная Локоть равнялся Большой локоть, С 16-го века такая мера длины, как локоть постепенно Про не очень умных людей говорят: «Нос с локоть, а Известно, что 99 % людей не могут лизнуть свой собственный локоть, а 90 % людей, которым об этом сообщили, сразу пытаются |
|
ПЯДЬ Малая пядь — принято Великая пядь (Большая пядь) – Пядь с кувырком – Раньше пядями мерили иконы, В быту это была мерка для толщины снега. Про очень умных говорят: «Семи пядей во лбу», как бы |
|
АРШИН Одна из самых старинных мер длины (c 17-го века Корень «АР» в слове а р ш и н — в древнерусском Также считается, что слово «аршин» восходит к Аршин равен длине руки – от основания плеча до Купцы, продавая товар, как правило, мерили его своим аршином (линейкой) или по-быстрому – Как вы думаете, что означает пословица «Как аршин Во второй половине XVI века в торговле и |
|
САЖЕНЬ Наименование с а ж е н ь происходит от глагола Сажень одна из наиболее распространенных на Руси мер Маховая сажень — Косая сажень — Существовали так же морская сажень равная 183 см, городовая В строительстве и при межевании земельных участков Если про мальчика или мужчину скажут «Косая сажень в Древние зодчие не знали метров и см, им были Прежде всего оказалось, что сажень – это не совсем |
Конечно,
такие измерения были очень приблизительными. Потребность в точном счете, в
вычислении времени и расстояния появилась гораздо позже, лишь с приходом нового
этапа в развитии человечества: с появлением скотоводства, земледелия и
торговли.
Только
потребность людей в более точном измерении расстояния вызвала необходимость
искать универсальный способ измерения. Представьте себе, как неудобно было
измерять расстояние шагами, а ткань локтями. У продавца и у покупателя ноги и
руки могли быть разной длины…
С
данной проблемой в начале XII века попытался справиться Генрих I, король
Англии. И тем самым внес существенный “вклад” в историю возникновения мер
длины. Он издал указ, согласно которому, чтобы не было обмана, единственной
мерой длины для всех измерений установлена была длина локтя самого короля. За основную, в английском обиходе, меру
длины — ярд — указом короля Генриха 1(1101 год) было определено расстояние от
носа короля до конца среднего пальца вытянутой его руки. Длина ярда в настоящее
время равна 0,9144 метра.
Проходили
века, и только в 1791 году французскими учеными было найдено удобное и очень
важное для международных торговых отношений решение: универсальной единицей
длины была взята 1/40000000 (одна сорокамиллионная) часть Парижского меридиана.
Эту меру длины назвали “метр” (с греческого языка – “мера”). От слова “метр”
произошло слово “дециметр” (1/10 часть метра), “сантиметр” (1/100 часть метра)
и “миллиметр” (1/1000 часть метра).
В
1892 году гениальный русский химик Дмитрий Иванович Менделеев(1834 – 1907)
покинул Петербургский университет и с того же года стал во главе Главной палаты
мер. В 1899 году был издан разработанный Д.И. Менделеевым новый закон о мерах.
В
1869 году Петербургская академия наук обратилась к ученым учреждениям всего
мира с призывом заняться пересмотром оснований метрической системы для того,
чтобы она могла стать международной. Комиссия, состоящая из представителей 24
государств, собралась в Париже и в начале 1872 года утвердила эталон метра.
В
СССР метрические меры введены во всеобщее употребление в 1918 году. В России существовала долгое время
смешанная система мер длины. Наряду с древнерусскими старинными мерами длины —
верстой, аршином и вершком, до принятия в 1918 году метрической системы мер
использовались введенные Петром І европейские меры длины — фут, дюйм,
географическая и морская мили.
. Для популяризации новых
мер поэт В.В.Маяковский написал стихотворные тексты, посвященные новым мерам.
Серия «А» (о
метрической мере длины)
Принято в торговом
народе
Аршин отмерять
в этом роде:
Расстояние от пальца
до плеча
Привыкли аршином величать.
Так и метр отмерить
вам можно:
Приблизительно
От пальцев до
плеча противоположного.
Не хитрая машина –
ладонью отмерять четверть
аршина.
Растопырь
большой и указательный пальцы:
Приблизительно четверть
аршина отвалится.
Сантиметр тож
Легко измерить
с помощью ладош.
Чтоб 10
сантиметров отмерить мог,
Отложи ладонь не
вдоль, а поперек.
Запомни также
(трудности нет):
10
сантиметров — один дециметр.
Запомни, расчет
очень важен:
Два
метра — приблизительно сажень.
Рисуем, чтоб каждый
запомнить мог:
четыре сантиметра
— один вершок.
Запомни, эта работа
не тяжка:
Один сантиметр — четверть
вершка.
Заруби на носу,
торговый люд:
Три
дециметра — один фут.
Узнаем, не
тратя догадок уйму:
2½ сантиметра равняются
дюйму
Единицы
измерения длины у разных народов
Знание,
хотя и приближенное, длины единиц мер древних народов дает возможность
установить некоторые интересные факты.
В
Сибири была в употреблении мера расстояния бука; это расстояние, на котором
человек перестает видеть раздельно рога быка.
Эстонские
моряки измеряют расстояния трубками. Так называлось у моряков расстояние,
проходимое судном при нормальной скорости за время, пока курится набитая
табаком трубка.
В
Испании такой же мерой расстояния служит сигара, в Японии — лошадиный башмак,
то есть путь, проходимый лошадью, пока износится привязываемая к ее ногам
соломенная подошва, заменявшая в Японии подкову.
У
многих народов была мера расстояния стрела — дальность полета стрелы. Наши
выражения: не подпускать “на ружейный выстрел”, позднее — “на
пушечный выстрел” напоминают о подобных единицах расстояний.
Дюйм
единица длины, которая первоначально была длиною сустава большого пальца.
Одновременно с дюймом была уточнена длина другой меры — фута, — употреблявшейся
с древних времен многими народами. Фут — это средняя длина ступни человека
(английское слово “foot”— “ступня”).
Система мер длины
Египта была следующая:
·
ладонь = 4 пальцам (= 2,2 см),
·
локоть = 6 ладоням (рукам).
Для истории учения о мерах
(метрологии) интересен факт, что в Египте существовало два локтя:
·
локоть народный — 6 ладоням = 24 пальцам,
·
локоть царский = 7 ладоням = 28 пальцам.
Эталоны локтя, дошедшие
до нас, имеют длину около 525 миллиметров – это царские локти. Кирпичи пирамид
имеют стандартную длину–450 миллиметров; это народный локоть. Таким образом, в
Египте существовали две меры локтей. Это давало возможность использовать меры
для той эксплуатации народных масс, которая получила распространение у всех
народов в феодальный период, когда владелец земли получал плату большими
мерами, сам же платил меньшими.
Древние
римляне для измерения расстояний использовали длину ступни (фут). Для измерения
меньших величин они делили ступню (фут) на 12 пальцев (ширина большого пальца).
Эта величина носила название унция.
Большие
расстояния римляне измеряли в пасах, причем каждый пас представлял собой
величину, равную двум шагам. Тысяча пасов составляли одну милю. Слово
“миля” происходит от латинского милле, что означает
“тысяча”.
Арабы,
измеряли небольшие расстояния самой маленькой старинной мерой длины — маковым
зернышком. Несколько маковых зернышек равнялись одному ячменному зерну, а
несколько ячменных зерен — одной фаланге указательного пальца.
Список источников:
1.
https://xn--j1ahfl.xn--p1ai/library/lepbuk_starinnie_meri_dlini_na_rusi_093015.html
2.
https://mognovse.ru/xsi-istoriya-mer-dlini.html
3.
http://repetitor-problem.net/istoriya-mer-dlinyi
4.
https://inger.com.ua/istoriya_lineyki/
5.
http://multiurok.ru/index.php/files/zanimatelnye-zadaniia-o-starinnykh-merakh-dliny-i.html
Длиной принято обозначать расстояние между двумя точками какого-либо отрезка. Это может быть прямая, ломаная или замкнутая линия. Вычислить длину можно довольно простым путем, если знать некоторые другие показатели отрезка.
Если вам нужно найти длину стороны квадрата, то это не составит труда, если вам известна его площадь S. В связи с тем, что все стороны квадрата имеют одинаковую длину, вычислить величину одной из них можно по формуле: a = √S.
В случае, когда требуется просчитать длину стороны прямоугольника, воспользуйтесь значениями его площади s и длины другой стороны b. Из формулы a=S/b вы получите искомое значение.
Чтобы определить длину окружности, то есть замкнутой линии, которая образует круг, воспользуйтесь значениями: r – ее радиусом и D – диаметром. Диаметр можно вычислить, умножив радиус окружности на 2. Известные вам значения подставьте в формулу определения длины окружности: C=2πr=πD, где π=3,14.
Для вычисления длины обычного отрезка воспользуйтесь методом эксперимента. То есть возьмите линейку и измеряйте.
Для того чтобы вычислить длину стороны такой фигуры, как треугольник, вам понадобятся размеры двух других сторон, а также величины углов. Если вы имеете дело с прямоугольным треугольником, и один из его углов равен 60 градусам, то величину его катета можно определить по формуле a=c*cosα, где c – гипотенуза треугольника, а α – угол между гипотенузой и катетом.
Помимо этого, если вы располагаете такими известными величинами, как высота b и площадь S треугольника, то длину стороны, которая является основанием, можно узнать благодаря формуле a=2√S/√√b.
Что касается правильного многоугольника, то длину его стороны можно просчитать, руководствуясь формулой an=2R*sin(α/2)=2r*tg(α/2), где R – радиус описанной окружности, r – радиус вписанной окружности, n – количество углов.
Если вы хотите вычислить длину равносторонней фигуры, вокруг которой описана окружность, то сделать это можно по формуле an=R√3, где R – радиус окружности, n – количество углов фигуры.