Как определить расчетный пролет балки (плиты, перемычки)

При расчете любого изгибаемого элемента, будь то плита, балка или перемычка, прежде всего, следует определить расчетный пролет. При переводе объемных конструкций в плоскую расчетную схему очень важно задаться правильными размерами элементов. Ведь в расчетной схеме все просто: балка – это стержень, а опора – точка. На самом же деле опора имеет свой размер – глубину опирания, и балка не зависает на краях стены (от точки до точки), часть ее работает в пролете, но часть – «отдыхает» на опорах.
Создавая расчетную схему, мы сталкиваемся с двумя величинами: реальной длиной балки и расстоянием в свету между опорами. Какую из этих величин следует принять за расчетную? Если брать полную длину балки, это будет неверно, т.к. все-таки та ее часть, которая лежит на опоре, не подвержена таким напряжениям, как в пролете. Но брать за расчетную длину расстояние между опорами можно только в отдельных случаях, ниже мы рассмотрим, что да как.
Далеко не всегда расчетная длина балки совпадает с пролетом в свету между опорами.
Есть два варианта размера расчетного пролета.
1) Если опирание жесткое, т.е. балка защемлена на опоре (либо является частью монолитной конструкции), то расчетный пролет L0 равен расстоянию в свету между опорами.
2) Если же опирание шарнирное, то расчетный пролет всегда больше этого расстояния.
Рассмотрим глубже определение расчетного пролета при шарнирном опирании элемента. Во-первых, следует четко определиться с требованиями глубины опирания шарнирных элементов (поможет статья “В чем разница между шарнирным опиранием и жестким защемлением”). Если вы делаете расчет шарнирно опираемой железобетонной балки (плиты и т.п.), глубина ее опирания должна быть не более высоты сечения – иначе, это будет уже защемление или переходное состояние между шарниром и защемлением, а там и расчет другой, и длина расчетного пролета – согласно пункту 1. Т.е. если вы плиту толщиной 200 мм опираете на 450 мм с каждой стороны, то пользоваться нижеприведенным расчетом не следует.
Для ленивых во многих учебниках есть правило: L0 = 1.05L, т.е. берем расстояние между опорами в свету и умножаем на 1,05.
Но сейчас мы постараемся понять, в чем же суть увеличения расчетного пролета, и как поточнее его определить.
При расчете балки мы привыкли получать реакции на опоре в виде сосредоточенных сил.

Но если рассмотреть точнее, нагрузка от балки на опору передается в виде распределенной нагрузки, причем даже не равномерно распределенной: максимальная ее величина расположена у края опоры, а к концу балки она сходит на нет.

По общепринятым правилам перевода распределенной нагрузки в сосредоточенную, положение сосредоточенной нагрузки будет в центре тяжести треугольника, т.е. на расстоянии 1/3 от края опоры. В этом же месте будет расположена искомая реакция. А расстояние между этими реакциями будет равно расчетному пролету.
Таким образом, если глубина опирания балки с одной стороны равна А, а с другой стороны В, то расчетный пролет мы найдем по формуле:
L0 = L + A/3 + B/3.
Если же глубина опирания с двух сторон одинаковая и равна А, то
L0 = L + 2A/3.
Такое увеличение расчетного пролета по отношению к реальному (в районе 5%) дает определенный запас прочности и приближает нас к реальному положению вещей – ведь длина балки может быть разной, а глубина опирания обычно одинаковая. И пять процентов при трехметровом пролете значительно отличается от пяти процентов при восьмиметровом.
Надеюсь, статья оказалась вам полезной.
Расчет длин пролетов
на прямых участках пути

(3.1)
где К – номинальное
натяжение контактных проводов, даН;
Вк.доп
– наиболее
допустимое горизонтальное отклонение
контактных
проводов от оси
токоприемника в пролете;
Вк.доп
– равно 0,5 м,
на прямых участков пути;
Вк.доп
– равно 0,45 м,
на кривых участках пути;
А – зигзаг
контактного провода;
a
– равно 0,3 м – на прямых участков пути,
а равна 0,4 м – на кривых участков пути;
К1
– определяется
по выражению
Определяем
коэффициент К1
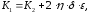
(3.2)
где 
и
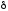
– коэффициенты учитывающие пульсацию
ветра;

– коэффициент динамичности.
Определяем
коэффициент К2
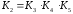
(3.3)
Расчёт максимально
допустимых длин пролёта осложнён тем,
что в формулу входит величина Рэ
– эквивалентная удельная нагрузка,
равномерно распределяется по длине
пролёта, вызывает такое же горизонтальное
отклонение контактного провода как и
нагрузка от струн в средней части пролёта
определяем по формуле
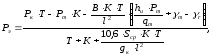
(3.4)
где Т – натяжение
несущего троса контактной подвески а
расчетном
режиме,
даН;
РТ
– ветровая нагрузка на несущий трос,
даН/м;
gT
– результирующая нагрузка на несущий
трос, даН/м;
L
–длина пролета.
Средняя длина
струны в средней части пролета, м
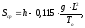
(3.5)
где h
– конструктивная высота контактной
подвески, м;
g
– нагрузка от веса проводов контактной
подвески, даН/м;
То
– натяжение несущего троса при
беспроводном положении
контактных
проводов, даН.
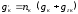
(3.6)
Определяем длины
пролетов для всех характерных точек
местности.
3.1 Второстепенные пути станции
Пользуемся
методом последовательных приближений.
Принимаем
РЭ
равно 0, К1
равно1.
Подставив
числовые значения в формулу (3.1), получаем
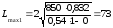 м
м
Определяем
коэффициент К2
Подставив числовые
значения в формулу (3.2), получаем
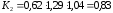
Определяем
коэффициент К1
Подставив числовые
значения в формулу (3.2), получаем
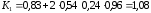
Определяем нагрузку
от веса контактных проводов в подвеске
Подставив числовые
значения в формулу (3.6), получаем
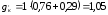 даН/м
даН/м
Определяем длину
пролета в соответствии с коэффициентом
К1
Подставив числовые
значения в формулу (3.1), получаем
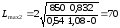 м
м
Определяем среднюю
длину струны
Подставив числовые
значения в формулу (3.5), получаем
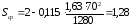 м
м
Определяем удельную
эквивалентную нагрузку
Подставив числовые
значения в формулу (3.4), получаем
 даН/м
даН/м
Определяем длину
пролета с учетом РЭ
Подставив числовые
значения в формулу (3.1), получаем
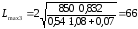 м
м
3.2 Главные пути станции и выемка более 6 метров
Пользуемся методом
последовательных приближений.
Принимаем РЭ
равно 0, К равно 1.
Подставив числовые
значения в формулу (3.1), получаем
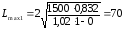 м
м
Определяем
коэффициент К2
Подставив числовые
значения в формулу (3.2), получаем
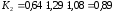
Определяем
коэффициент К1
Подставив числовые
значения в формулу (3.2), получаем
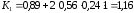
Определяем нагрузку
от веса контактных проводов в подвеске
Подставив числовые
значения в формулу (3.6), получаем
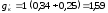 даН/м
даН/м
Определяем длину
пролета в соответствии с коэффициентом
К1
Подставив числовые
значения в формулу (3.1), получаем
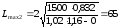 м
м
Определяем среднюю
длину струны
Подставив числовые
значения в формулу (3.5), получаем
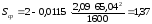 м
м
Определяем удельную
эквивалентную нагрузку
Подставив числовые
значения в формулу (3.4), получаем
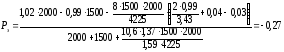
даН/м
Определяем длину
пролета с учетом РЭ
Подставив числовые
значения в формулу (3.1), получаем
 м
м
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как определить расчетный пролет балки
При расчете любого изгибаемого элемента, будь то плита, балка или перемычка, прежде всего, следует определить расчетный пролет. При переводе объемных конструкций в плоскую расчетную схему очень важно задаться правильными размерами элементов. Ведь в расчетной схеме все просто: балка – это стержень, а опора – точка. На самом же деле опора имеет свой размер – глубину опирания, и балка не зависает на краях стены (от точки до точки), часть ее работает в пролете, но часть – «отдыхает» на опорах.
Создавая расчетную схему, мы сталкиваемся с двумя величинами: реальной длиной балки и расстоянием в свету между опорами. Какую из этих величин следует принять за расчетную? Если брать полную длину балки, это будет неверно, т.к. все-таки та ее часть, которая лежит на опоре, не подвержена таким напряжениям, как в пролете. Но брать за расчетную длину расстояние между опорами можно только в отдельных случаях, ниже мы рассмотрим, что да как, так же смотрите расчет элементов строительных конструкций.
Далеко не всегда расчетная длина балки совпадает с пролетом в свету между опорами.
Есть два варианта размера расчетного пролета. Если опирание жесткое, т.е. балка защемлена на опоре (либо является частью монолитной конструкции), то расчетный пролет L0 равен расстоянию в свету между опорами. Если же опирание шарнирное, то расчетный пролет всегда больше этого расстояния.
Рассмотрим глубже определение расчетного пролета при шарнирном опирании элемента. Во-первых, следует четко определиться с требованиями глубины опирания шарнирных элементов (поможет статья «В чем разница между шарнирным опиранием и жестким защемлением»). Если вы делаете расчет шарнирно опираемой железобетонной балки (плиты и т.п.), глубина ее опирания должна быть не более высоты сечения – иначе, это будет уже защемление или переходное состояние между шарниром и защемлением, а там и расчет другой, и длина расчетного пролета – согласно пункту 1. Т.е. если вы плиту толщиной 200 мм опираете на 450 мм с каждой стороны, то пользоваться нижеприведенным расчетом не следует.
Но сейчас мы постараемся понять, в чем же суть увеличения расчетного пролета, и как поточнее его определить.
При расчете балки мы привыкли получать реакции на опоре в виде сосредоточенных сил.
