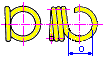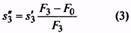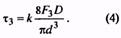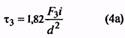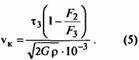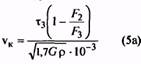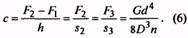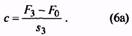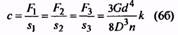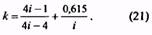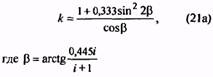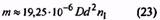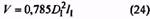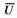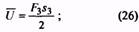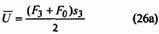Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.
Виды деформации
Деформация – это изменение формы, или размеров тела.
Есть несколько видов деформации:
- сдвиг;
- кручение;
- изгиб;
- сжатие/растяжение;
Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.
Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.
Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.

Рис. 1. пластиковая линейка, деформированная изгибом – а) и кручением – б)
В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.
Растяжение пружины
Рассмотрим подробнее деформацию растяжения на примере пружины.
Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина (L_{0}) пружины.

Рис. 2. Сравнивая длину свободной пружины с длиной нагруженной, можно найти ее удлинение
Подвесим теперь к пружине груз. Пружина будет иметь длину (L), указанную на рисунке справа.
Сравним длину нагруженной пружины с длиной свободно висящей пружины.
[ large L_{0} + Delta L = L ]
Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину (L_{0}).
[ large boxed{ Delta L = L — L_{0} }]
( L_{0} left(text{м} right) ) – начальная длина пружины;
( L left(text{м} right) ) – конечная длина растянутой пружины;
( Delta L left(text{м} right) ) – кусочек длины, на который растянули пружину;
Величину ( Delta L ) называют удлинением пружины.
Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.
Примечание: Отношение – это дробь. Относительное – значит, дробное.
[ large boxed{ frac{Delta L }{ L_{0}} = frac{ L — L_{0}}{L_{0} } = varepsilon } ]
( varepsilon ) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.
Расчет силы упругости
Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.
Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.
Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.

Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо
Закон Гука
Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.
[ large boxed{ F_{text{упр}} = k cdot Delta L }]
Эту формулу назвали законом упругости Гука.
( F_{text{упр}} left( H right) ) – сила упругости;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости).
Какие деформации называют малыми
Закон Гука применяют для малых удлинений (деформаций).
Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.
Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.
Как рассчитать коэффициент жесткости
Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.

Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости
Так как силы взаимно компенсируются, в правой части уравнения находится ноль.
[ large F_{text{упр}} — m cdot g = 0 ]
Подставим в это уравнение выражение для силы упругости
[ large k cdot Delta L — m cdot g = 0 ]
Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:
[ large boxed{ k = frac{ m cdot g }{Delta L} }]
(g) – ускорение свободного падения, оно связано с силой тяжести.
Соединяем две одинаковые пружины
В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.
Параллельное соединение пружин
На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.

Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины
Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две параллельные пружины:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]
Умножим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{параллел}} = 2k_{1} } ]
Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной
Последовательное соединение пружин
Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.
Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.
На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).
Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений

Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины
Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две последовательные пружины:
[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{послед}} cdot 2 = k_{1} ]
Разделим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{послед}} = frac{k_{1}}{2} } ]
Коэффициент жесткости (k_{text{послед}}) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной
Потенциальная энергия сжатой или растянутой пружины
Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.

Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией
Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).
Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:
[ large boxed{ E_{p} = frac{k}{2} cdot left( Delta L right)^{2} }]
( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости) пружины.
Выводы
- Упругие тела – такие, которые сопротивляются деформации;
- Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
- Деформация – изменение формы, или размеров тела;
- Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
- Удлинение пружины – это разность ее конечной и начальной длин;
- Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
- Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
- Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
- А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.

NettaBlackRouse
+10
Решено
8 лет назад
Физика
5 – 9 классы
Что бы пружина удлинилась до 15 см нужно приложить силу 45Н, а до 18 см – 72Н. Как найти длину пружины в недеформирлванном состоянии?
Смотреть ответ
2
Ответ
3
(8 оценок)
16

flustikova
8 лет назад
Светило науки – 5 ответов – 0 раз оказано помощи
Обозначим длину недеформированной пружины за L, тогда пружина растянется на (15-L) и (18-L)см в 1 и 2 случае соответственно.
k(15-L)=45,
k(18-L)=72,
делишь одно уравнение на второе, решаешь и получаешь L=10 см
(8 оценок)
Ответ
2
(6 оценок)
3

ваапкек
8 лет назад
Светило науки – 125 ответов – 0 раз оказано помощи
ΔL=l0-l ( Закон Гука)
(6 оценок)
https://vashotvet.com/task/7350582
Основные
понятия
Пружина
растяжения — это спирально-цилиндрическая
пружина, витки которой прилегают друг
к другу. Пружина подвергается действию
противоположно направленных усилий,
приложенных вдоль ее оси.
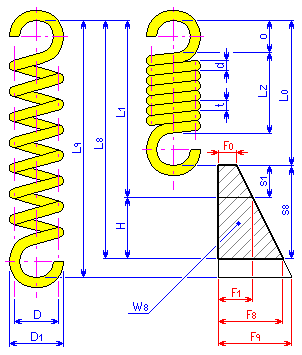
Размеры
|
d |
диаметр |
|
D |
средний |
|
D1 |
наружный |
|
D2 |
внутренний |
|
H |
рабочая |
|
t |
шаг |
|
o |
высота |
|
sx |
деформация |
|
Lx |
длина |
|
Fx |
рабочая |
|
W8 |
энергия |
|
x |
индекс, |
Навивка
-
Вправо
(стандарт) -
Влево
(должна отображаться соответствующая
надпись)
Состояния
-
Свободное:
пружина не нагружена (индекс 0) -
Предварительная
нагрузка: пружина с минимальной рабочей
нагрузкой (индекс 1) -
Полная
нагрузка: пружина с максимальной рабочей
нагрузкой (индекс 8) -
Предел:
пружина вдавлена до касания витков
(индекс 9).
Зацепы
пружин растяжения
Высота
зацепа пружины растяжения
![]()
Где:
|
L0 |
длина |
|
LZ |
длина |
Часто
используемые зацепы пружин растяжения
|
Тип |
Изображение |
|
Половина |
|
|
Обычно |
|
|
Полный |
|
|
Используется |
|
|
Полный |
|
|
Когда |
|
|
Полный |
|
|
Обычно |
|
|
Поднятый |
|
|
Обычно |
|
|
Два |
|
|
Используется |
|
|
Два |
|
|
Когда |
Расчет
пружин в метрических единицах
Общие
формулы расчета
Коэффициент
использования материала
Наружный
диаметр пружины
D1 =
D + d [мм]
Где:
|
D |
средний |
|
|
d |
диаметр |
Внутренний
диаметр пружины
D2 =
D – d [мм]
Где:
|
D |
средний |
|
|
d |
диаметр |
Рабочая
деформация
H
= L81=
s81[мм]
Где:
|
L8 |
длина |
|
|
L1 |
длина |
|
|
s8 |
деформация |
|
|
s1 |
деформация |
Высота
зацепа пружины
Где:
|
L0 |
длина |
|
|
LZ |
длина |
Индекс
пружины
c
= D/d [-]
Где:
|
D |
средний |
|
|
d |
диаметр |
Поправочный
коэффициент Валя
Где:
|
c |
индекс |
|
|
LZ |
длина |
Начальное
растяжение
![]()
Где:
|
d |
диаметр |
|
|
0 |
напряжение |
|
|
D |
средний |
|
|
Kw |
поправочный |
Общая
сила, действующая в пружине
Где:
|
d |
диаметр |
|
|
G |
напряжение |
|
|
D |
средний |
|
|
Kw |
поправочный |
|
|
G |
модуль |
Жесткость
пружины
Где:
|
d |
диаметр |
|
|
G |
модуль |
|
|
D |
средний |
|
|
n |
количество |
|
|
F8 |
рабочее |
|
|
F1 |
рабочее |
|
|
H |
рабочая |
Расчет
конструкции пружины
При
проектировании пружины подбирается
диаметр проволоки, количество витков
и длина свободной пружины L0 для
заданной нагрузки, материала и сборочных
размеров.
![]()
Если
рассчитанная пружина не соответствует
ни одному значению диаметра проволоки
для данного напряжения 0 согласно
формуле, расчет пружины повторяется с
использованием скорректированного
значения напряжения в свободном состоянии
из рекомендуемого диапазона.
![]()
Пружине
без начального растяжения соответствует
средний рекомендуемый шаг витков t =
0,35 D [мм].
Если
рассчитанная пружина не соответствует
ни одному значению диаметра проволоки
для выбранного шага, расчет пружины
повторяется с использованием
скорректированного значения шага из
рекомендуемого диапазона 0,3 D ≤ t ≤ 0,4
D [мм].
Конструкция
пружины определяется с учетом условия
прочности 8≤ usA и
рекомендуемых диапазонов некоторых
геометрических параметров пружины:
L0≤ D
и L0≤ 31,5
д и 4 ≤ D/d ≤16 и n 2.
Задание
нагрузки, материала и сборочных размеров
пружины
Вначале
выполняется проверка входных величин
для расчета.
Затем
вычисляется длина пружины в свободном
состоянии.
![]()
После
расчета выбирается диаметр проволоки,
количество витков и диаметры пружины
– так, чтобы высота зацепа соответствовала
выбранному типу зацепа. Кроме того,
должны выполняться упомянутые выше
прочностные и геометрические условия.
Конструкция пружины должна удовлетворять
по диаметрам всем заданным начальным
условиям. При отсутствии таких
дополнительных условий предельный
диаметр пружины устанавливается по
геометрическим условиям для
минимально/максимально допустимого
диаметра проволоки.
Отбираются
все диаметры проволоки (от меньшего к
большему), которые проходят по прочностным
и геометрическим условиям. Проверяются
высота зацепа и количество витков. Если
все условия выполнены, расчет конструкции
завершается, и текущие значения параметров
принимаются в качестве его результатов,
независимо от того, как прошел бы расчет
при других подходящих диаметрах
проволоки. Таким образом, полученная
пружина имеет минимально возможный
диаметр проволоки и минимально возможное
количество витков.
Вычисленное
значение высоты зацепа должно находиться
в пределах d ≤ o ≤ 30 d. Комбинация
диаметра проволоки, количества витков
и диаметра пружины должна давать в итоге
такую высоту зацепа, которая удовлетворяет
его типу. Вначале в качестве типа зацепа
берется полный виток, затем, если он не
годится–полный виток внутри и т.д.
Задание
нагрузки, материала и диаметра пружины
Вначале
выполняется проверка входных величин
для расчета.
После
проверки выбирается диаметр проволоки,
количество витков, длина пружины в
свободном состоянии и сборочные размеры
пружины – так, чтобы высота зацепа
соответствовала выбранному типу зацепа.
Кроме того, должны выполняться прочностные
и геометрические условия. Если сборочный
размер L1 или
L8 взят
из спецификации или значение рабочей
деформации пружины ограничено, конструкция
пружины должна соответствовать этому
условию. В остальных случаях предельные
значения сборочных размеров пружины и
ее длины в свободном состоянии определяются
геометрическими условиями для заданного
диаметра пружины и минимального/максимального
допустимого диаметра проволоки.
Формула
для проектирования пружины по заданному
диаметру проволоки.
где
значение 8 =
0,85 A используется
в качестве величины напряжения материала
пружины при кручении в полностью
нагруженном состоянии.
Если
для данного диаметра проволоки не
удается подобрать подходящую комбинацию
размеров пружины, расчетная процедура
оценивает другие диаметры проволоки.
Они проверяются, начиная от меньшего к
большему, до тех пор пока не будет
достигнуто такое количество витков,
при котором высота зацепа удовлетворяет
всем условиям. Расчет конструкции
завершается, и текущие значения параметров
принимаются в качестве его результатов,
независимо от того, как прошел бы расчет
при других подходящих диаметрах
проволоки. Таким образом, полученная
пружина имеет минимально возможный
диаметр проволоки и минимально возможное
количество витков.
Вычисленное
значение высоты зацепа должно находиться
в пределах d ≤ o ≤ 30 d. Для
высоты, вычисленной таким способом,
выбирается соответствующий тип зацепа.
Комбинация диаметра проволоки, количества
витков, длины пружины в свободном
состоянии и сборочных размеров пружины
должна давать в итоге такую высоту
зацепа, которая удовлетворяет его типу.
Вначале в качестве типа зацепа берется
полный виток, затем, если он не
годится–полный виток внутри и т.д.
Задание
максимального рабочего усилия, материала,
сборочных размеров и диаметра пружины
Вначале
выполняется проверка входных величин
для расчета.
Затем
подбирается диаметр проволоки, количество
витков, длина свободной пружины и
минимальное рабочее усилие F1 таким
образом, чтобы высота зацепа пружины
соответствовала выбранному типу зацепа.
Кроме того, должны выполняться прочностные
и геометрические условия.
Формула
для проектирования пружины по заданному
диаметру проволоки.
где
значение 8 =
0,9 A используется
в качестве величины напряжения материала
пружины при кручении в полностью
нагруженном состоянии.
Если
для данного диаметра проволоки не
удается подобрать подходящую комбинацию
размеров пружины, расчетная процедура
оценивает другие диаметры проволоки.
Они проверяются, начиная от меньшего к
большему, до тех пор пока не будет
достигнуто такое количество витков,
при котором высота зацепа удовлетворяет
всем условиям. Расчет конструкции
завершается, и текущие значения параметров
принимаются в качестве его результатов,
независимо от того, как прошел бы расчет
при других подходящих диаметрах
проволоки. Таким образом, полученная
пружина имеет минимально возможный
диаметр проволоки и минимально возможное
количество витков.
Проверочный
расчет пружины
Расчет
соответствующих значений сборочных
размеров и рабочего отклонения для
указанной нагрузки, материала и размеров
пружины.
Сначала
проверяются расчетные входные значения.
Затем на основании приведенных ниже
формул вычисляются сборочные размеры.
Длина
предварительно нагруженной пружины
![]()
Длина
полностью нагруженной пружины
![]()
Где:
|
L0 |
длина |
|
|
F1 |
рабочая |
|
|
D |
средний |
|
|
n |
количество |
|
|
G |
модуль |
|
|
d |
диаметр |
|
|
F8 |
рабочее |
Рабочая
деформация
H
= L18[мм]
Расчет
рабочих сил
Расчет
соответствующих сил, действующих в
пружинах в рабочем состоянии для
указанного материала, сборочных размеров
и размеров пружины. Сначала проверяются
и рассчитываются входные данные, а затем
выполняется расчет рабочих сил с помощью
следующих формул.
Минимальное
рабочее усилие
![]()
Максимальное
рабочее усилие
![]()
Расчет
выходных параметров пружины
Эта
часть является общей для всех типов
расчета пружины. Расчет производится
в следующем порядке.
Коэффициент
высоты зацепа
![]()
Жесткость
пружины
Длина
части с витками
|
Пружина |
|
|
Lz = |
|
|
Пружина |
|
|
Lz = |
Деформация
предварительно нагруженной пружины
s1 =
L1 –
L0 [мм]
Полная
деформация пружины
s8 =
L8 –
L0 [мм]
Напряжение
при кручении материала пружины в
состоянии предварительной нагрузки
Напряжение
материала пружины при кручении при
полном нагружении
Предельное
усилие в пружине
![]()
Деформация
в предельном состоянии
![]()
Где:
|
k |
жесткость |
|
|
F9 |
рабочее |
|
|
F0 |
начальное |
Предельная
длина пружины
L9 =
L0 +
s9 [мм]
Энергия
деформации пружины
![]()
Длина
развернутой проволоки
|
l |
|||
|
Где |
|||
|
для |
|||
|
l0 = D |
|||
|
для |
|||
|
l0 = |
|||
|
для |
|||
|
l0 = |
|||
|
для |
|||
|
l0 = |
|||
|
для |
|||
|
l0 = D |
|||
|
для |
|||
|
l0 = |
|||
|
для |
|||
|
l0 = |
|||
|
для |
|||
|
l0 = |
Масса
пружины
![]()
Собственная
частота колебаний пружины
Проверка
нагрузки пружины
8≤ us
A
Обзор
используемых переменных:
|
d |
диаметр |
|
k |
жесткость |
|
D |
средний |
|
D1 |
наружный |
|
D2 |
внутренний |
|
F |
обобщенное |
|
G |
модуль |
|
H |
рабочая |
|
c |
индекс |
|
Kw |
поправочный |
|
l |
длина |
|
L |
обобщенная |
|
LZ |
длина |
|
m |
масса |
|
n |
количество |
|
o |
высота |
|
t |
шаг |
|
s |
обобщенная |
|
us |
коэффициент |
|
|
плотность |
|
|
напряжение |
|
A |
допустимое |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Виды деформации
Деформация – это изменение формы, или размеров тела.
Есть несколько видов деформации:
- сдвиг;
- кручение;
- изгиб;
- сжатие/растяжение;
Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.
Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.
Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.
Рис. 1. пластиковая линейка, деформированная изгибом – а) и кручением – б)
В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.
Расчет силы упругости
Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.
Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.
Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.
Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо
Закон Гука
Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.
[ large boxed{ F_{text{упр}} = k cdot Delta L }]
Эту формулу назвали законом упругости Гука.
( F_{text{упр}} left( H right) ) – сила упругости;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости).
Какие деформации называют малыми
Закон Гука применяют для малых удлинений (деформаций).
Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.
Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.
Как рассчитать коэффициент жесткости
Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.
Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости
Так как силы взаимно компенсируются, в правой части уравнения находится ноль.
[ large F_{text{упр}} — m cdot g = 0 ]
Подставим в это уравнение выражение для силы упругости
[ large k cdot Delta L — m cdot g = 0 ]
Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:
[ large boxed{ k = frac{ m cdot g }{Delta L} }]
(g) – ускорение свободного падения, оно связано с силой тяжести.
Расчет винтовых цилиндрических одножильных пружин растяжения и сжатия.
Рассмотрим расчет винтовых цилиндрических одножильных пружин растяжения и сжатия. Основные геометрические параметры винтовых цилиндрических пружин из проволоки круглого поперечного сечения (см. рис. 1): d — диаметр проволоки; Dн и D — наружный и средний диаметры пружины; c=D/d — индекс пружины; t — шаг пружины; α — угол подъема витков; L0 — длина развернутой пружины (без учета зацепов пружины). Податливость пружины прямо пропорциональна ее индексу c. Для увеличения податливости пружины индекс с принимают возможно большим; практически c=4…12.
Значения индекса с пружины принимают в зависимости от диаметра проволоки:
| d, мм | < 2,5 | 3…5 | 6…12 |
| c | 5…12 | 4…10 | 4…9 |
Рис. 1
С увеличением индекса пружины той же жесткости можно сократить ее длину путем увеличения диаметра, а с уменьшением индекса можно уменьшить диаметр пружины путем увеличения ее длины.
Рис. 2
В любом поперечном сечении витка пружины растяжения или сжатия при работе возникают (рис. 2, а) сила F, направленная по осевой линии пружины, и момент М=FD/2, вектор которого перпендикулярен осевой линии пружины. Сила F раскладывается на поперечную F1=F cos α и продольную F2=F sin α силы. При разложении момента М по осевой линии витка пружины и перпендикулярному ему направлению в поперечном сечении проволоки пружины возникают: крутящий T=FD cos α/2 и изгибающий Ми=FD sin α/2 моменты. Так как угол α<10…12°, то изгибающий момент Ми значительно меньше крутящего Т, а продольная сила F2 значительно меньше поперечной силы F1 но, как показывают расчеты, касательные напряжения сдвига значительно меньше касательных напряжений кручения, поэтому для упрощения расчета пружин на прочность обычно учитывают лишь крутящий момент T, при этом приближенно принимают cos α=1, т. е. T=М=FD/2. Таким образом, расчет винтовой цилиндрической пружины растяжения или сжатия из проволоки круглого поперечного сечения производят по формуле
где τ — расчетное максимальное напряжение в поперечных сечениях витков пружины; [τ] — допускаемое напряжение для проволоки пружины; k — коэффициент влияния на напряжение кривизны витков и поперечной силы; F — максимальная растягивающая или сжимающая сила. Формулой пользуются при проверочном расчете пружины, когда ее размеры известны.
Значения коэффициента k принимают в зависимости от индекса пружины:
| c | 4 | 5 | 6 | 8 | 10 | 12 |
| k | 1,37 | 1,29 | 1,24 | 1,17 | 1,14 | 1,11 |
Рис. 3
Допускаемое напряжение [τ] пружин при статических нагрузках можно принимать по графикам (рис. 3), где отдельные кривые относятся к пружинам из проволоки:
- 1 — вольфрамовой и рояльной;
- 2 — хромованадиевой;
- 3 — углеродистой, закаленной в масле;
- 4 — углеродистой холоднотянутой;
- 5 — моиель-металла;
- 6 — фосфористой бронзы;
- 7 — специальной латуни.
При пульсирующей нагрузке с небольшим числом циклов допускаемые напряжения [τ] следует принимать в 1,25…1,5 раза ниже, чем по графикам.
При проектировочном расчете пружины диаметр проволоки
значением индекса с пружины задаются. Диаметр d проволоки, вычисленный по формуле, окончательно согласовывают с соответствующим ГОСТом для пружинной проволоки.
Средний диаметр D пружины и наружный диаметр DH определяют по формулам
и
При расчетах различают следующие силы пружины (см. рис. 1 , а, б): при предварительной деформации — F1 при рабочей деформации (соответствует наибольшему принудительному перемещению подвижного звена в механизме) — F2; при максимальной деформации «(допускаемой) — F3. Соответственно в формулах F=F3.
Обычно пружину устанавливают с действующей на нее начальной нагрузкой F1=(0,1…0,5)F2. Максимальная сила пружины F3=(1,05..,1,66)F2. При изменении силы пружины от F1 до F2 жесткость пружины
где h — рабочий ход пружины, значение которого назначают или вычисляют по условиям работы механизма. Жесткость одного витка пружины где G — модуль сдвига материала проволоки пружины. Для стали G=80000 МПа и, следовательно, для стальной пружины где С1 — в Н/мм; d — в мм.
Число рабочих витков пружины
Полное число витков
где n2=1,5…2 — число опорных витков.
Деформация пружины
Подставив в формулу вместо F силы F1, F2, F3, получим деформации: λ1 — предварительную, λ2 — рабочую и λ3 — максимальную. Максимальная деформация одного витка пружины
Шаг пружины в ненагруженном состоянии: для пружины сжатия
для пружины растяжения
Высота пружины при максимальной деформации
где n3 — число зашлифованных витков. Высота пружины в свободном состоянии для пружины сжатия для пружины растяжения
Высоту пружины при предварительной и рабочей деформации легко определить из (рис. 1, а, б). Длина развернутой пружины (без учета зацепов пружины растяжения)
Более подробный геометрический расчет винтовых цилиндрических пружин сжатия и растяжения из стальной проволоки круглого сечения дан в ГОСТ 13765-68.
Соединяем две одинаковые пружины
В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.
Параллельное соединение пружин
На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.
Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины
Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две параллельные пружины:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]
Умножим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{параллел}} = 2k_{1} } ]
Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной
Последовательное соединение пружин
Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.
Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.
На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).
Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений
Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины
Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две последовательные пружины:
[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
Not Found
Пример
1. Пружина сжатия. Дано: F1 = 20 Н; F2 = 80Н; h = 30мм; D1 = 10÷
12мм; Vmax = 5 м/с; NF ≥ 1∙107. Пользуясь табл. 1, убеждаемся, что при заданной выносливости пружину следует отнести к классу I. По формуле (2), пользуясь интервалом значений 8 от 0,05 до 0,25 (формула (1)], находим граничные значения силы F3, a именно:
F3 = F2/(1-0,05) ÷ F2/(1-0,25)=84 ÷ 107 Н
В интервале от 84 до 107 Н (ГОСТ 13766—86) пружин класса I, разряда 1 имеются следующие силы F3 ; 85; 90; 95; 100 и 106 Н (табл. 11). Исходя из заданных размеров диаметра и стремления обеспечить наибольшую критическую скорость, останавливаемся на витке со следующими данными (номер позиции 355): F3 = 106 H; d = 1,80 мм; D1 = 12 мм; с1 =97,05 Н/мм; s′3 = 1,092 мм. Учитывая, что для пружин класса I норма напряжений τ = 0,3Rm (см. табл. 2), находим, что для найденного диаметра проволоки из углеродистой холоднотянутой стали расчетное напряжение τ33 ≈ 0,3 · 2100 = = 630 Н/мм2. Принадлежность к классу I проверяем путем определения отношения vmax / vk , для чего предварительно определяем критическую скорость по формуле (5)при d = 0,25:
Полученная величина указывает на отсутствие соударения витков, и, следовательно, выбранная пружина удовлетворяет заданным условиям, но так как пружины класса II относятся к разряду ограниченной выносливости, то следует учитывать комплектацию машины запасными пружинами с учетом опытных данных. Определение остальных размеров производим по формулам табл. 10. По формуле (6) находим жесткость пружины c = (F2-F1)/h= (80-20)/30=2.0 Н/мм. Число рабочих витков пружины определяем по формуле (7): n = c1/c = 36,58/2,0 = 18,29 ≈ 18,5 Уточненная жесткость имеет значение c = c1/n = 36,58/18,5= 1,977 ≈ 2,0 Н/мм. При полутора нерабочих витках полное число витков находим по формуле (8): n1 = n + n2 = 18,5 + 1,5 = 20 По формуле (9) определяем средний диаметр пружины D =
11,5 — 1,40 = 10,1 мм. Деформации, длины и шаг пружины вычисляем по формулам [(11)-(18)]:
На этом определение размеров пружины и габарита узла (размер ℓ1) заканчивается. Следует отметить, что некоторое увеличение выносливости может быть достигнуто при использовании пружины с большей величиной силы F3 , чем найденная в настоящем примере. С целью выяснения габаритов, занимаемых такой пружиной, проделаем добавочный анализ: остановимся, например, на витке со следующими данными по ГОСТ 13770-86 (позиция 313); F3 = 106 H; d = 1,4 мм; D1 = 10,5 мм; с1 =50,01 Н/мм; s′3 = 2,119 мм. Находим τ = 1150 Н/мм2 и производим расчет в той же последовательности: d = 1- (F2/F3)=1- (80/106) = 0,245; vk= (1150 · 0,245) /35,1 = 8,05 м/с, vmax / vk = 5,0/8,05 =0,622 Очевидно, что у этой пружины создается большой запас на несоударяемость витков. Далее в рассмотренном ранее порядке находим n=50,01/2,0= 25,01 ≈ 25,0 Уточненная жесткость с =50,01/25,0
≈ 2,0 Н/мм;
Таким образом, устанавливаем, что применение пружины с более высокой силой F3
хотя и привело к большему запасу на несоударяемость витков, но оно сопровождается увеличением габарита узла (размер ℓ1) на 15,3 мм. Можно показать, что если выбрать виток с большим диаметром, например D1 = 16 мм (ГОСТ 13770-86, номер позиции 314), то тогда потребуется расширить узел по диаметру, но при этом соответственно уменьшится размер ℓ1.
Пример 2. Пружина сжатия. Дано: F1 = 100 Н; F2 =
250 Н; h
=
100 мм; D1 = 15 ÷ 25 мм; vmax = 10 м/с Независимо от заданной выносливости на основании формулы (5) можно убедиться, что при значениях d, меньших 0,25 [формула (1)], все одножильные пружины, нагружаемые со скоростью vmax более 9,4 м/с, относятся к III классу. По формуле (2) с учетом диапазона значений d для пружин класса III от 0,1 до 0,4 [формула (1)] находим границы сил
;
F3=F2/(1-0,1)÷ F2/(1-0,4) = 250/0,9 ÷ 250/0,6 =278÷417 Н Верхние значения силы F3
,
как видно из табл. 2 ГОСТ 13764—86, не могут быть получены из числа одножильных конструкций, поэтому, учитывая коэффициенты d = 0,15 ÷ 0,40 [формула (1)] для трехжильных пружин, устанавливаем новые пределы F3, по формуле (2): F3
=
294÷417 Н. Для указанного интервала в ГОСТ 13774-86 имеются витки со следующими силами
F3:
300; 315; 335; 375 и 400 (табл. 16а). Исходя из заданных размеров диаметра и наименьших габаритов узла, предварительно останавливаемся на витке со следующими данными (номер позиции 251): F3 = 300 Н; d = 1,4 мм; d1
=
3,10 ; D1
=
17 мм; с1 = 50,93 Н/мм; s′3= 5,900 мм. Согласно ГОСТ 13764—86 для пружин класса III τ3 = 0,6 Rm
.
Используя ГОСТ 9389-75, определяем напряжение для найденного диаметра проволоки τ3 = 0,6 · 2300 = 1380 МПа. Принадлежность к классу проверяем путем определения величины отношения vmax / vk для чего предварительно находим d и критическую скорость по формулам (1), (2) и (5а): d = 1-(F2/F3) = 1-(250/300)= 0,167; vk= (1380 · 0,167)/32,4 = 7 м/с vmax / vk= 10,0 /7,0=1,43 > 1. Полученное неравенство свидетельствует о наличии соударения витков и о принадлежности пружины к классу III. Определение остальных параметров производится по формулам табл. 10. По формуле (6) находим жесткость c = (F2- F1) / h = 250-100/100= 1,5 Н/мм. Число рабочих витков пружины вычисляют по формуле (7): n = c1/c = 50,9/1,5 = 33,9 ≈ 34,0 Уточненная жесткость
с
= c1 /n = 50,9/34,0 = 1,49 ≈ 1,5 Н/мм. Полное число витков находят по формуле (8): n1 = n + 1,5 = 34,0 + 1,5 = 35,5 . По формуле (9а) определяют средний диаметр пружины D
=
D1 — d1
=
17 — 3,10 = 13,90 мм. Деформации, длины и шаг пружины находят по формулам в табл. 10 [формулы (10а), (11)-(18а)]: s1 = F1/c = 100/1,5 = 66,7 мм; s2 = F2/c = 250/1,5 = 166,7 мм; s3 = F3/c = 300/1,5 =200 мм ; i = D/d1=13,90/3,10 =4,5; ℓ3
= (n1+1) d1∆ = (35,5 + 1) 3,10 · 1,021 = 115,5 мм; ℓ0=
ℓ3 + s3 = 115,5 + 200 = 315,5 мм; ℓ1 =ℓ0 — s1 = 315,5 — 66,7 = 248,8 мм; ℓ2 =ℓ0 — s2
=
315,5 — 166,7 = 148,8 мм
t
= s’3
+
d1∆ = 5,9 + 3,10 · 1,021 = 9,19 мм.Проанализируем пружины, соответствующие трем ближайшим значениям F3
,
взятым из ГОСТ 13774—86 (пружины класса III, разряда 1) для рассмотренного случая (табл. 16а). Вычисления, проделанные в аналогичном порядке, показывают, что для трех соседних сил F3 образуется шесть размеров пружин, удовлетворяющих требованиям по величине наружного диаметра. Сведения о таких пружинах приведены ниже.
| F3,H | 300 | 315 | 335 | |||
| d , мм | 1,4 | 1,6 | 1,4 | 1,6 | 1,4 | 1,6 |
| d1 , мм | 3,10 | 3,50 | 3,10 | 3,50 | 3,10 | 3,50 |
| D1 , мм | 17,0 | 24,0 | 16,0 | 22,0 | 15,0 | 21,0 |
| vmax / vk | 1,43 | 1,50 | 1,16 | 1,21 | 0,942 | 0,984 |
| ℓ0, мм | 317,0 | 273,9 | 355,1 | 309,0 | 405,1 | 337,0 |
| ℓ1, мм | 250,4 | 207,2 | 288,4 | 242,3 | 338,4 | 270,3 |
| ℓ2, мм | 150,4 | 107,2 | 188,4 | 142,3 | 238,4 | 170,3 |
| n1, мм | 36,0 | 20,0 | 44,5 | 27,0 | 56,0 | 31,0 |
| V,мм3 | 57000 | 93000 | 58000 | 92000 | 60000 | 93000 |
Из этих данных следует, что с возрастанием F3 уменьшается отношение vmax / vk и, в частности, может быть устранено соударение витков, но вместе с этим возрастают габариты по размерам ℓ1. С возрастанием диаметров пружин габариты по размерам ℓ1 уменьшаются, однако существенно возрастают объемы пространств, занимаемые пружинами. Следует отметить, что если бы для рассматриваемого примера, в соответствии с требованиями распространенных классификаций, была выбрана пружина класса I, то при одинаковом диаметре гнезда (
D1 ≈ 18 мм) даже самая экономная из них потребовала бы длину гнезда ℓ1 = 546 мм, т. е. в 2,2 раза больше, чем рассмотренная выше. При этом она была бы в 11,5 раза тяжелее и, вследствие малой критической скорости (vk = 0,7 м/с), практически неработоспособной при заданной скорости нагружения 10 м/с.
Пример
3. Пружина растяжения. Дано: F1 = 250 Н; F2 = 800 Н; h = 100 мм; D1 = 28 ÷ 32 мм; NF ≥ 1· 105.На основании ГОСТ 13764—86 по величине
NF
устанавливаем, что пружина относится к классу II (см. табл. 1.) По формуле (2) находим силы
F3
, cоответствующие предельной деформации: F3 = F2/(1-0,05) ÷ F2/(1-0,10) =842÷ 889 Н. В интервале сил 842—889 Н в ГОСТ 13770—86 для пружин класса II, разряда 1 (номер пружины 494) имеется виток со следующими параметрами: F3 = 850 Н; D1
=
30 мм; d = 4,5 мм; с1 = 242,2 Н/мм; s’3 =3,510 мм (см. табл. 14). По заданным параметрам с помощью формулы (6) определяем жесткость пружины:
с = (
F2- F1)/h = (800-250)/100 = 5,5 H/мм. Число рабочих витков находим по формуле (7): n = c1/c = 242,2 / 5,5 ≈ 44.Деформации и длины пружины вычисляют по формулам [(11)-(17а)]: s1=F1/c = 250/5,5 =45,5 мм; s2 = F2/c = 800/5,5 = 145,5 мм; s3 = F3/c = 850/5,5 = 154,5 мм ; ℓ’0
=
(n +1)d= (44+1)4,5 = 202,5 мм; ℓ1 =ℓ0 + s1 = 202,5 + 45,5 = 248,0 мм; ℓ2 =ℓ0 + s2
=
202,5 +145,5 = 348,0 мм; ℓ3 =ℓ0 + s3
=
202,5 +154,5 = 357,0 мм. Размер ℓ2 с учетом конструкций зацепов определяет длину гнезда для размещения пружины растяжения в узле. Размер ℓ3 с учетом конструкций зацепов ограничивает деформацию пружины растяжения при заневоливании. Трехжильные пружины (угол свивки 24º). Жесткость s1=F1/s1 = F2/s2 =F3/s3 = 30000d4k/D3n = H/мм; k= (1+ 0,333· sin22b)/ cosb b = arctg (0,445 i / i+1) , i = D/d1Напряжение τ3 = 1,82 F3 i /d2МПа Полученные значения жесткости должны совпадать с вычисленными по формуле (6). Полученные значения напряжений должны совпадать с указанными в ГОСТ 13764—86 для соответствующих разрядов с отклонениями не более + 10
%.
404 Not Found
The requested URL /bottom.php was not found on this server.
Additionally, a 404 Not Found error was encountered while trying to use an ErrorDocument to handle the request.
Потенциальная энергия сжатой или растянутой пружины
Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.
Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией
Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).
Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:
[ large boxed{ E_{p} = frac{k}{2} cdot left( Delta L right)^{2} }]
( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости) пружины.
Плоские спиральные пружины
Плоские спиральные пружины изготавливают из тонкой высококачественной углеродистой ленты. Применяют в качестве заводных, аккумулирующих энергию, что возможно благодаря высокой гибкости ленты, позволяющей иметь большой угол поворота валика до нескольких десятков оборотов. Пружины обычно помещают в барабан для обеспечения смазки и придания им определённых внешних размеров. В неответственныхмеханизмах используютспиральные пружины и без барабанов. Внутренний конец пружины крепят, как правило, к валику, а наружный к барабану.
КПД спиральных пружин определяется отношением работы, производимой пружиной при развёртывании к работе, затрачиваемой на заводку, и колеблется в пределах 0,6-0,7 в зависимости от смазки. Следует избегатьпружин повышенной толщины ленты, так как они работают не плавно, что ведёт к перенапряжению в материале пружины и к её поломке. Толщину ленты пружины b
следует выбирать из условия
, , где r
–
радиусвалика, на который наматывается пружина. Уравнение оси пружиннойленты, плотно навитой на валик, в полярных координатах ,где ρ–текущий полярный радиус, φ- полярный угол. Начальный радиус ρ1 соответствует углу φ1.Конечный радиус ρ2 соответствуетуглуφ2 = φ1 +2n, где n—число оборотов спирали пружины равное .
Рабочая длина ленты пружиныL
= .
При жёстком закреплении концов пружины в корпусе и на валике, она испытывает чистый изгиб. Напряжение изгиба ленты ,где h
–
высота ленты, М
– изгибающиймомент. Отсюда требуемая высота ленты
.
Суммарный угол закручивания ,где J
– момент инерции сечения ленты.
Максимальный момент на валике пружины ,где nр
– максимальное расчётноечисло витков пружины.
nр =n2 – n1 , где n2
– число витков заведенной пружины в барабане, n1 – число витков свободной пружины (вне барабана).
Рабочее число оборотов барабанаφпри расчёте следует увеличивать на 0,5-1,5 для покрытия потерь на трение.
Минимальный момент на валике пружины , где np.min = n – n1 ; n –число витков спущенной пружины (в барабане).
Тарельчатые пружины

выбирают равным 2-3, а угол подъема образующей конуса 2-60. В соответствии с ГОСТ 3957 тарельчатые пружины выполняют наружным диаметром 28-300мм, толщиной
s = 1-20мм
, высотой конуса
f= 0,6-9мм
. Рабочая нагрузка пружин до 520 кН. Упругая осадка пружин допускается до 0,8f.
Тарельчатые пружины, имея небольшие габариты по высоте, представляют значительные преимущества по сравнению с другими пружинами для больших нагрузок при высокой потребной жёсткости, что и определяет область их применения. На рис. б показано обычное выполнение пакета пружин для максимальной податливости. На рис. в
показан пакет с тройным набором односторонних пружин для повышения несущей способности. На рис.
г
пакет пружин с промежуточными шайбами, более активно демпфирующих энергию колебаний.
Тарельчатые пружины штампуют, как правило, из листовой кремнистой стали 60С2А. Для повышения несущей способности их обжимают пере закалкой до полного распрямления, в результате чего в них возникают остаточные напряжения обратного знака.
Точный расчёт пружин довольно сложен и их обычно подбирают по таблицам ГОСТа 3957.
Приближённая зависимость между осевой силой Р
и осевым сжатием
λ1
одного элемента пружины , где
E и μ
– модуль упругости и коэффициент Пуассона материала пружины;
А
– коэффициент, принимаемый по приведенному графику.
Наибольшее напряжение сжатия на внутренней кромке пружины .
Коэффициенты К, К0, К1
также принимают по графику. Допускаемые напряжения по приведенной формуле выбирают весьма высокими, достигающими при статической нагрузке для кремнистой стали
1600 – 2000 МПа
.
Выводы
- Упругие тела – такие, которые сопротивляются деформации;
- Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
- Деформация – изменение формы, или размеров тела;
- Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
- Удлинение пружины – это разность ее конечной и начальной длин;
- Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
- Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
- Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
- А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.
10. Формулы и способы расчета пружин из стали круглого сечения по ГОСТ 13765-86 в ред. 1990г.
Пружина сжатия
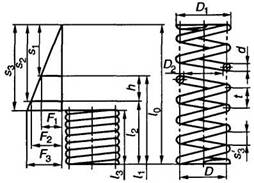
Пружина растяжения
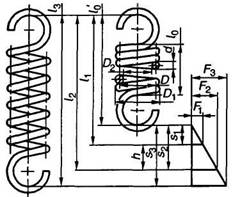
|
Наименование параметра |
Обозначение |
Расчетные формулы и значения |
|
1. Сила пружины при предварительной деформации, Н |
F1 |
Принимаются в зависимости от нагрузки пружины |
|
2. Сила пружины при рабочей деформации (соответствует наибольшему принудительному перемещению подвижного звена в механизме), Н |
F2 |
|
|
3. Рабочий ход пружины, мм |
h |
|
|
4. Наибольшая скорость перемещения подвижного конца пружины при нагружении или разгрузке, м/с |
Vmax |
|
|
5. Выносливость пружины, число циклов до разрушения |
NF |
Продолжение табл. 10
|
Наименование параметра |
Обозначение |
Расчетные формулы и значения |
|
6. Наружный диаметр пружины, мм |
D1 |
Предварительно назначают с учетом конструкции узла. Уточняются по таблицам ГОСТ 13766-86-ГОСТ 13776-86 |
|
7. Относительный инерционный зазор пружины сжатия. Для пружин растяжения служит ограничением максимальной деформации |
δ |
δ = 1-F2/F3. (1) Для пружин сжатия классов I и IIδ=0,05…0,25; для пружин растяжения δ=0,05…0,10; для одножильных пружин класса IIIδ=0,10…0,40; для трехжильных класса IIIδ=0,15…0,40 |
|
8. Сила пружины при максимальной деформации, Н |
F3 |
F3=F2/(1-δ) (2) Уточняется по таблицам ГОСТ 13766-86-ГОСТ 13776-86 |
|
9. Сила предварительного напряжения (при навивке из холоднотянутой и термообработанной проволоки), Н |
F0 |
F0= (0,1… 0,25) F3 |
|
10. Диаметр проволоки, мм |
d |
Выбирается по таблицам ГОСТ 13764-86-ГОСТ 13776-86 |
|
11. Диаметр трехжильного троса, мм |
d1 |
|
|
12. Жесткость одного витка пружины, Н/мм |
c1 |
|
|
13. Максимальная деформация одного витка пружины, мм |
s’3 (при F0=0) s”3 (при F0>0) |
Выбирается по таблицам ГОСТ 13764-86-ГОСТ 13776-86
|
|
14. Максимальное касательное напряжение пружины, Н/мм2 (Коэффициент k см. п. 35) |
τ3 |
Назначается по табл. 2 ГОСТ 13764-86. При проверке
Для трехжильных пружин
|
|
15. Критическая скорость пружины сжатия, м/с (Максимальная скорость подвижного звена механизма vmax должна быть равна или меньше vK, т.е. vK > vmax) |
vк |
Для трехжильных пружин
|
|
16. Модуль сдвига, Н/мм2 |
G |
Для пружинной стали G = 7,85·104 |
|
17. Динамическая (гравитационная) плотность материала, Н·с2/м4 |
Р |
p = γ/g, где g-ускорение свободного падения, м/с2; γ – удельный вес, Н/м3. Для пружиннойстали р = 8·103 |
|
18. Жесткость пружины, Н/мм |
с |
Для пружин с предварительным напряжением
Для трехжильных пружин
|
|
19. Число рабочих витков пружины |
n |
n = c1/c (7) |
|
20. Полное число витков пружины |
n1 |
n1 = n+ n2, (8) где n2 – число опорных витков |
|
21. Средний диаметр пружины, мм |
D |
D = D1 – d = D2 + d Для трехжильных пружин D = D1– d1= D2+ d1(9a) |
|
22. Индекс пружины |
i |
i = D/d (10) Для трехжильных пружин i= D/d1 (10а) Рекомендуется назначать от 4 до 12 |
Продолжение табл. 10
|
Наименование параметра |
Обозначение |
Расчетные формулы и значения |
||||
|
23. Коэффициент расплющивания троса в трехжильной пружине, учитывающий увеличение сечения витка вдоль оси пружины после навивки |
Δ |
Для трехжильного троса с углом свивкиβ=24° определяется по таблице, приведенной ниже |
||||
|
i |
40 |
45 |
50 |
55 |
60 |
7,0 и более |
|
Δ |
1,029 |
1,021 |
1,015 |
1,010 |
1,005 |
1,000 |
|
24. Предварительная деформация пружины, мм |
s1 |
s1=F1/c (11) |
||||
|
25. Рабочая деформация пружины, мм |
s2 |
s2= F2/c (12) |
||||
|
26. Максимальная деформация пружины, мм |
s3 |
s3= F3/c (13) |
||||
|
27. Длина пружины при максимальной деформации, мм |
l3 |
l3 = (n1 + 1 – n3)d, (14) где n3 – число обработанных витков. Для трехжильных пружин l3 = (n + l)d1Δ. (14а) Для пружин растяжения с зацепами l3 = l0 + s3 |
||||
|
28. Длина пружины в свободном состоянии, мм |
l0 |
l0=l3+s3 (15) |
||||
|
29. Длина пружины растяжения без зацепов в свободном состоянии, мм |
l0‘ |
l0‘ = (n1+1)d (15а) |
||||
|
30. Длина пружины при предварительной деформации, мм |
1l |
l1 = l0-s1. (16) Для пружин растяжения l1= l0+s1(16а) |
||||
|
31. Длина пружины при рабочей деформации, мм |
l2 |
l2=l0-s2. (17) Для пружин растяжения l2=l0+s2 (17а) |
||||
|
32. Шаг пружины в свободном состоянии, мм |
t |
t = s’3+d. (18) Для трехжильных пружин t = s’3+d1Δ. (18а) Для пружин растяжения t = d(18б) |
||||
|
33. Напряжение в пружине при предварительной деформации, Н/мм2 |
τ1 |
|
||||
|
34. Напряжение в пружине при рабочей деформации, Н/мм2 |
τ2 |
|
||||
|
35. Коэффициент, учитывающий кривизну витка пружины |
k |
Для трехжильных пружин
|
||||
|
36. Длина развернутой пружины (для пружин растяжения без зацепов), мм |
l |
|
||||
|
37. Масса пружины (для пружин растяжения без зацепов), кг |
m |
|
||||
|
38. Объем, занимаемый пружиной (без учета зацепов пружины), мм3 |
V |
|
||||
|
39. Зазор между концом опорного витка и соседним рабочим витком пружины сжатия, мм |
λ |
Устанавливается в зависимости от формы опорного витка |
||||
|
40. Внутренний диаметр пружины, мм |
D2 |
D2=D1-2d (25) |
||||
|
41. Временное сопротивление проволоки при растяжении, Н/мм2 |
Rm |
Устанавливается при испытаниях проволоки или по ГОСТ 9389-75 и ГОСТ 1071-81 |
||||
|
42. Максимальная энергия, накапливаемая пружиной, или работа деформации, МДж |
|
Для пружин сжатия и растяжения без предварительного напряжения
для пружин растяжения с предварительным напряжением
|
Методика определения размеров пружин по ГОСТ 13765-86.
1. Исходными величинами для определения размеров пружин являются силы F1 и F2, рабочий ход h, наибольшая скорость перемещения подвижного конца пружины при нагружении или при разгрузке vmах, выносливость NF и наружный диаметр пружины D1 (предварительный).
Если задана только одна сила F2, то вместо рабочего хода h для подсчета берут величину рабочей деформации s2, соответствующую заданной силе.
2. По величине заданной выносливости NF предварительно определяют принадлежность пружины к соответствующему классу по табл. 1.
3. По заданной силе F2 и крайним значениям инерционного зазора δ вычисляют по формуле (2) значение силы F3.
4. По значению F3, пользуясь табл. 2, предварительно определяют разряд пружины.
5. По табл. 11-17 находят строку, в которой наружный диаметр витка пружины наиболее близок к предварительно заданному значению D1. В этой же строке находят соответствующие значения силы F3 и диаметра проволоки d.
6. Для пружин из закаливаемых марок сталей максимальное касательное напряжение τ3 находят по табл. 2, для пружин из холоднотянутой и термообработанной τ3 вычисляют с
учетом значений временного сопротивления Rm. Для холоднотянутой проволоки Rm определяют из ГОСТ 9389-75, для термообработанной – из ГОСТ 1071-81.
7. По полученным значениям F3 и τ3, aтакже по заданному значению F2 по формулам (5) и (5а) вычисляют критическую скорость vK и отношение vmax/vK, подтверждающее или
отрицающее принадлежность пружины к предварительно установленному классу.
При несоблюдении условий vmax/vK<1 пружины I и II классов относят к последующему классу или повторяют расчеты, изменив исходные условия. Если невозможно изменение исходных условий, работоспособность обеспечивается комплектом запасных пружин.
8. По окончательно установленному классу и разряду в соответствующей таблице на параметры витков пружин, помимо ранее найденных величин F3, D1, и d, находят величины c1 и s3, после чего остальные размеры пружины и габариты узла вычисляют по формулам (6)… (25).