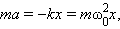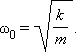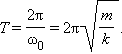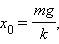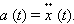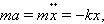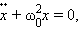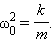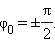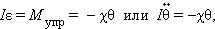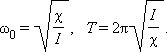Как найти длину пружины в равновесии

2016-09-19   

На конце невесомого стержня длиной $l$, шарнирно прикреплённого к стене, находится груз массой $m$ (см. рисунок). Стержень удерживается в равновесии в горизонтальном положении пружиной жёсткостью $k$, прикреплённой на расстоянии $l_{1}$ от шарнира, причём угол между пружиной и стержнем равен $alpha$. Найдите частоту малых колебаний груза относительно положения равновесия.

Решение:

Пусть груз сместился от положения равновесия на величину $x$. Обозначим длину пружины в положении равновесия через $x_{0}$, длину пружины после смещения груза — через $x_{1}$, величину смещения точки соединения пружины и стержня — через $x^{ prime}$, и найдём удлинение пружины $Delta x$. Применяя к треугольнику $ABD$ (рис.) теорему косинусов, получим:

$x_{1}^{2} approx x^{ prime 2} + x_{0}^{2} – 2x^{ prime} x_{0} cos left ( frac{ pi}{2} + alpha right )$.

Здесь учтено, что смещения $x$ и $x^{ prime}$ малы, и поэтому $angle CAD approx pi /2$. Перенося $x_{0}^{2}$ в левую часть уравнения, применяя формулу разности квадратов и учитывая, что $x_{1} — x_{0} = Delta x, x_{1} + x_{0} approx 2x_{0}$, получим: $2 x_{0} Delta x approx x^{ prime 2} + 2 x^{ prime} x_{0} sin alpha$. Пренебрегая величиной $x^{ prime 2}$ ввиду её малости, найдём удлинение пружины: $Delta x approx x^{ prime} sin alpha$. Смещения $x$ и $x^{ prime}$ связаны между собой соотношением: $x^{ prime} = frac{l_{1}}{l}x$, поэтому окончательно для удлинения пружины имеем:

$Delta x approx frac{l_{1} sin alpha}{l} x$.

Запишем теперь выражения для кинетической энергии груза $W$ и потенциальной энергии $U$ запасённой в пружине:

$W = frac{mv^{2}}{2}; U = frac{k Delta x^{2}}{2} = frac{k}{2} left ( frac{l_{1} sin alpha}{l} right )^{2} x^{2}$.

Здесь $v = dx/dt$ — скорость, соответствующая координате $x$. Квадрат искомой круговой частоты равен отношению коэффициентов при $x^{2}$ и при $v^{2}$ в выражениях для $U$ и $W$. Поэтому окончательно получаем:

$omega_{0} = frac{l_{1} sin alpha}{l} sqrt{ frac{l}{m} }$.

Заметим, что по аналогии с колебаниями груза, подвешенного на пружине, начальную потенциальную энергию пружины, имеющуюся в положении равновесия нашей системы, а также потенциальную энергию груза в поле силы тяжести можно не учитывать, потому что коэффициент при $x^{2}$ в выражении для $U$ от этого не меняется.

A straight wire rotates with constant angular speed $omega$ about one of its end points (the origin $O$) in a horizontal plane containing $e_1$ and $e_2$. A bead of mass $m$ is free to slide along the wire, but is connected to $O$ by a spring coiled around the wire, as illustrated below. The spring has natural length $a$ and spring constant $k$. The magnitude of the frictional force is proportional to the radial speed of the bead with a frictional constant $K$.

Assuming $omeganeqomega_s$, find the equilibrium length of the spring, say $R$.

I have worked through previous parts of the question and have derived the equation of motion of the bead which is $$ddot{r}+alphadot{r}=(omega^2-omega_s^2)r+aomega_s^2,$$ where $alpha=frac{K}{m}$ and $omega_s^2=frac{k}{m}$.

But I struggle on how to derive the equilibrium length of the spring, I don’t know how to start.

Thank you.

Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.

Виды деформации

Деформация – это изменение формы, или размеров тела.

Есть несколько видов деформации:

• сдвиг;
• кручение;
• изгиб;
• сжатие/растяжение;

Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.

Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.

Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.

В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.

Растяжение пружины

Рассмотрим подробнее деформацию растяжения на примере пружины.

Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина (L_{0}) пружины.

Подвесим теперь к пружине груз. Пружина будет иметь длину (L), указанную на рисунке справа.

Сравним длину нагруженной пружины с длиной свободно висящей пружины.

[ large L_{0} + Delta L = L ]

Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину (L_{0}).

[ large boxed{ Delta L = L — L_{0} }]

( L_{0} left(text{м} right) )  – начальная длина пружины;

( L left(text{м} right) )  – конечная длина растянутой пружины;

( Delta L left(text{м} right) )  – кусочек длины, на который растянули пружину;

Величину ( Delta L ) называют удлинением пружины.

Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.

Примечание: Отношение – это дробь. Относительное – значит, дробное.

[ large boxed{ frac{Delta L }{ L_{0}} = frac{ L — L_{0}}{L_{0} } = varepsilon } ]

( varepsilon ) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.

Расчет силы упругости

Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.

Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.

Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.

Закон Гука

Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.

[ large boxed{ F_{text{упр}} = k cdot Delta L }]

Эту формулу назвали законом упругости Гука.

( F_{text{упр}} left( H right) ) – сила упругости;

( Delta L left(text{м} right) )  – удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) )  – коэффициент жесткости (упругости).

Какие деформации называют малыми

Закон Гука применяют для малых удлинений (деформаций).

Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.

Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.

Как рассчитать коэффициент жесткости

Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.

Так как силы взаимно компенсируются, в правой части уравнения находится ноль.

[ large F_{text{упр}} — m cdot g = 0 ]

Подставим в это уравнение выражение для силы упругости

[ large k cdot Delta L — m cdot g = 0 ]

Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:

[ large boxed{ k = frac{ m cdot g }{Delta L} }]

(g) – ускорение свободного падения, оно связано с силой тяжести.

Соединяем две одинаковые пружины

В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.

Параллельное соединение пружин

На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.

Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).

Одна пружина:

[ large k_{1} cdot Delta L = m cdot g ]

Две параллельные пружины:

[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]

Так как правые части уравнений совпадают, левые части тоже будут равны:

[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]

Умножим обе части полученного уравнения на число 2:

[ large boxed{ k_{text{параллел}} = 2k_{1} } ]

Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной

Последовательное соединение пружин

Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.

Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.

На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).

Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений

Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).

Одна пружина:

[ large k_{1} cdot Delta L = m cdot g ]

Две последовательные пружины:

[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]

Так как правые части уравнений совпадают, левые части тоже будут равны:

[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

[ large k_{text{послед}} cdot 2 = k_{1} ]

Разделим обе части полученного уравнения на число 2:

[ large boxed{ k_{text{послед}} = frac{k_{1}}{2} } ]

Коэффициент жесткости (k_{text{послед}}) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной

Потенциальная энергия сжатой или растянутой пружины

Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу,  например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.

Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).

Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:

[ large boxed{ E_{p} = frac{k}{2} cdot  left( Delta L right)^{2} }]

( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;

( Delta L left(text{м} right) )  – удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) )  – коэффициент жесткости (упругости) пружины.

Выводы

1. Упругие тела – такие, которые сопротивляются деформации;
2. Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
3. Деформация – изменение формы, или размеров тела;
4. Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
5. Удлинение пружины – это разность ее конечной и начальной длин;
6. Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
7. Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
8. Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
9. А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.

amely – 3 ноября, 2009 – 20:09

• версия для печати

Рисунок 2.2.1.

Круговая частота свободных колебаний груза на пружине находится из второго закона Ньютона:

откуда

Частота называется собственной частотой колебательной системы.

Период гармонических колебаний груза на пружине равен

При горизонтальном расположении системы пружина–груз сила тяжести, приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину , равную

и колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты и периода колебаний справедливы и в этом случае.

Строгое описание поведения колебательной системы может быть дано, если принять во внимание математическую связь между ускорением тела и координатой : ускорение является второй производной координаты тела по времени :

Поэтому второй закон Ньютона для груза на пружине может быть записан в виде

или

(*)

где

Все физические системы (не только механические), описываемые уравнением (*), способны совершать свободные гармонические колебания, так как решением этого уравнения являются гармонические функции вида

Уравнение (*) называется уравнением свободных колебаний . Следует обратить внимание на то, что физические свойства колебательной системы определяют только собственную частоту колебаний или период . Такие параметры колебательного процесса, как амплитуда _m и начальная фаза , определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени.

Если, например, груз был смещен из положения равновесия на расстояние и затем в момент времени отпущен без начальной скорости, то _m = , .

Если же грузу, находившемуся в положении равновесия, с помощью резкого толчка была сообщена начальная скорость то

Таким образом, амплитуда _m свободных колебаний и его начальная фаза определяются начальными условиями .

Существует много разновидностей механических колебательных систем, в которых используются силы упругих деформаций. На рис. 2.2.2 показан угловой аналог линейного гармонического осциллятора, совершающий крутильные колебания. Горизонтально расположенный диск висит на упругой нити, закрепленной в его центре масс. При повороте диска на угол возникает момент сил упругой деформации кручения:

Это соотношение выражает закон Гука для деформации кручения. Величина аналогична жесткости пружины . Второй закон Ньютона для вращательного движения диска записывается в виде (см. §1.23)

где – момент инерции диска относительно оси, проходящий через центр масс, – угловое ускорение.

По аналогии с грузом на пружине можно получить:

Крутильный маятник широко используется в механических часах. Его называют балансиром. В балансире момент упругих сил создается с помощью спиралевидной пружинки.

Колебания груза на пружине — формулы, уравнения и задачи

Теория периодичности относится к общей физике. Повторяемость некоторых процессов в течение времени определяют с помощью различных величин, например, угла, напряжённости, температуры. Для изучения явления удобно использовать маятник. Одним из его видов является пружина с грузом. Колебания в такой системе зависят от периода, частоты и амплитуды. Узнать эти параметры можно, зная начальные условия и уравнения, описывающие механическую работу.

Общие сведения

Колебания — это изменения какой-либо величины в точности или приблизительно повторяющиеся во времени. Если рассматривать процесс, с точки зрения механики, то он описывается положением тела. Повторение в точности является периодическим. Математически это можно записать формулой: x (t + T) = x (t), где T — время, в течение которого совершается одно полное колебание (период). Число циклов принято обозначать буквой N. Его находят как отношение времени к периоду: N = t / T.

При исследовании процесса не всегда бывает удобно оперировать временем, поэтому часто используют число колебаний за единицу времени. Эта величина называется частотой. Находят её количество по формуле: f = 1 / T. Доказать справедливость приведённого равенства просто. Число колебаний зависит от времени и частоты: N = f * t. Отсюда: f = N / t = (t / T) / t = 1 / T.

Очень важно не только понимать суть характеристик колебания, но и знать единицы его измерения. Вот основные из них:

• период — секунды (с);
• частота — герцы (Гц);
• число колебаний — безразмерная величина.

Если в течение времени меняется и координата, то периодически будет изменяться и скорость. Значит: vx (t + T) = Vx (t).

Исходя из верности равенства, можно сказать, что условие периодичности будет справедливо и для проекции, то есть изменения ускорения. Отсюда следует, что сила действующая на тело тоже будет переменной: Fx (t + T) = Fx (t).

При процессе также происходит изменение потенциальной и кинетической энергий. Действительно, так как в процессе колебания скорость не является постоянной величиной, то соответственно будет меняться кинетическая работа. Потенциальная же энергия зависит от координат. Например, если рассмотреть период колебаний пружинного маятника, то за это время тело переместится из нижнего положения в верхнее и вернётся обратно. Значит, координата физического объекта изменится от нуля до какого-то граничного значения.

Следует отметить, что периодичные движения обязательно будут происходить в той системе, в которой есть положение равновесия. Причём оно должно быть устойчивым. То есть существует равнодействующая сила, стремящаяся привести объект в положение, соответствующее покою. Поэтому для поддержания отклонений нужна дополнительная сила. Колебательную систему (осциллятор) под действием вынужденной периодической силы называют вынужденной.

Пружинный маятник

Это устройство является простейшим примером свободных колебаний. В его состав входит кронштейн, пружина и груз. В качестве последнего может выступать любое физическое тело. Масса пружины по сравнению с грузом считается малой и при исследованиях не учитывается.

При изучении такой системы важной задачей является измерение периода движения тела, подвешенного к пружине. Определение понятию пружинного маятника, которое даётся в учебниках по физике довольно обобщённое. Считается, что это конструкция, в которой тело, имеющее массу m, подвешено на упругой пружине обладающей жёсткостью K. При этом из состояния равновесия систему может вывести упругая сила F = — k * x, где: x- расстояние от середины пружинного элемента до поверхности прикреплённого к нему груза.

Можно выделить два достаточных условия возникновения свободных колебаний:

Суть изучения гармонических колебаний состоит в определении их частоты движения или периода. В пружинном маятнике, впрочем, как и в любой колебательной системе, параметры зависят от ряда характеристик. Из основных величин, описывающих процесс, можно выделить: массу груза и жёсткость. Поэтому задача и состоит в выяснении, как период зависит от этих двух параметров.

Во время экспериментов регулировать массу довольно легко. Для этого можно взять эталонные гири и, соединяя их, увеличивать вес. Жёсткость же пружины можно изменить, добавляя параллельно или последовательно к ней другое сжимающееся тело. Чтобы выяснить, как будет изменяться характеристика растягивающегося элемента, нужно знать, что же представляет собой параметр. Так, под жёсткостью тела понимают отношение силы упругости к удлинению: k0 = F / Δ L. Измеряется величина в ньютонах, делённых на метр (Н/м).

Исходя из правила, если соединить две пружины параллельно и деформировать их, то можно утверждать, что первый и второй элемент растянется на одинаковую длину ΔL. Значит, возникнет две одинаково направленных силы упругости. Отсюда равнодействующая будет равняться: K = 2F/ ΔL = 2k0. Для последовательного же соединения длина всей системы увеличится на 2 ΔL. Сила упругости будет равна F. Соответственно, жёсткость будет изменяться по формуле: K = F / 2ΔL = k0 / 2.

Зависимость периода

При проведении эксперимента можно исследовать пять различных комбинаций поведения груза на пружине — два варианта связаны с весом и три с жёсткостью. Чтобы выполнить опыт самостоятельно нужно будет взять вертикальный кронштейн, две одинаковые пружины и два равных по весу груза. Так как в реальности период будет довольно маленький, то для его измерения можно взять время, например, пятидесяти колебаний, а потом полученный результат разделить на это число. Подсчёт времени удобно выполнять с помощью секундомера.

Вычисленные результаты нужно занести в таблицу. Примерный порядок чисел должен получиться таким:

k m	m0	2m0
k0 / 2	0,68	0,93
k0	0,46	0,64
2k0	0.34	0,47

Эти данные можно проанализировать. Выводы будут следующими:

• с ростом массы физического тела период цикличности увеличивается;
• по мере увеличения жёсткости период колебаний уменьшается.

Приведённые утверждения, возможно, описать и количественно. Исходя из результатов, величины, стоящие в ячейке m0k0 и 2m02ko почти совпадают. С точки зрения физики, так и должно быть. Если взять грузик на пружине и измерить характеристику, а потом добавить к нему точно такую же систему, то период не поменяется. Это и можно наблюдать во время опыта. Значит, период движения зависит от того каким будет отношение массы к жёсткости.

По аналогии можно рассмотреть, как влияет жёсткость. Из эксперимента, видно, что если её увеличить дважды на одну и ту же величину, то она возрастёт в четыре раза, а значение обратное частоте уменьшится на это же число. Отсюда можно предположить, что период будет обратно пропорционален корню квадратному из жёсткости.

Объединив эти две гипотезы можно сделать заключение. Что период амплитуды колебаний груза на пружине будет прямо пропорционален корню квадратного из отношения массы к жёсткости: T = √(m / k). Проверить это утверждение можно по теории размерности. Подставив в формулу единицы измерения, получим: √(m / k) = √(кг / (Н/м)) = √(кг * м / Н). Учитывая, что ньютон — это отношение метра к секунде в квадрате или килограмму, умноженному на метр и делённому на секунду, размерное равенство примет вид: √(кг * м/Н) = √(c 2 * м/м) = √с 2 = с.

Для написания полной формулы в равенство нужно вести ещё коэффициент. Он будет равняться 2p. Значит, период колебаний пружинного маятника количественно описывается выражением: T = 2p * √ (m / k).

Примеры решения задач

Практические задания помогают лучше разобраться в теоретическом материале и запомнить нужные для решения формулы. Существуют различные примеры, с помощью которых можно довольно быстро проработать весь изученный курс. Вот два задания с подробным описанием решения на вычисления параметров пружинных колебаний тела. Разобравшись в них, можно переходить к самостоятельному вычислению более сложных примеров.

Задание № 1. Груз, подвешенный к пружине, перемещается циклически по вертикальной оси. За восемь секунд он совершил тридцать два колебания. Определить частоту. Итак, по условию задания дано время t = 8 c и число полного перемещения тела N = 32. Чтобы решить эту задачу нужно воспользоваться формулой нахождения периода: T = t / N. Все величины для этого есть: T = 8 c / 32 = 1 / 4 = 0,25 секунды. Частота связана с периодом выражением: f = 1 / T. После подстановки чисел получится ответ равный четырём герцам.

Задание № 2. Грузик совершает колебания на пружине с жёсткостью сто ньютон на метр. При этом максимальная скорость движения составляет два метра в секунду. Вычислить массу тела учитывая, что максимальная амплитуда отклонения от точки покоя составляет десять сантиметров. Силой трения пренебречь.

При решении примера нужно рассуждать следующим образом. Когда будет максимальное растяжение пружины, то скорость груза равна нулю: V1 = 0. Значит, кинетическая энергия тоже будет нулевой: Ek1 = 0.

В этот момент останется только потенциальная энергия вытянутой пружины Ep1. В положении равновесия скорость тела максимальная и равняется V = 2 м/с. Так как пружина в этот момент нерастянута и несжатая, то Ep = 0.

По закону сохранения энергии: Ek1 + Ep1 = Ek + Ep. Кинетическая работа при растянутой пружине равняется нулю, так же как и потенциальная в состоянии покоя, значит, Ep1 = (k * L 2 ) / 2, где L — удлинение, а k — жёсткость. Энергию же можно найти так: Ek = mV 2 / 2. Так как тело совершает колебания около положения равновесия, то вытянутость пружины будет равняться амплитуде.

Перед тем как непосредственно переходить к составлению итоговой формулы и вычислениям необходимо все значения измерений привести в соответствии с СИ. Так, амплитуда указана в сантиметрах, поэтому её нужно перевести в метры. Теперь можно переходить к составлению отношения и подстановки данных: (k * L 2 ) / 2 = mV 2 / 2. Отсюда: m = (k * L) / V 2 = (100 Н/м * 0,1 2 м) / 2 2 м/с = 1 / 4 = 0,25 килограмма.