Как найти длину пружины зная массу

На этой странице сайта вы найдете ответы на вопрос Как найти L0(начальная длина пружины) если известны L, масса и коофицент жесткости пружины?,
относящийся к категории Физика. Сложность вопроса соответствует базовым
знаниям учеников 5 – 9 классов. Для получения дополнительной информации
найдите другие вопросы, относящимися к данной тематике, с помощью поисковой
системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и
задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям.
Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы
помогут найти нужную информацию.

Мы уже неоднократно пользовались динамометром – прибором для измерения сил. Познакомимся теперь с законом, позволяющим измерять силы динамометром и обуславливающим равномерность его шкалы.

Известно, что под действием сил возникает деформация тел – изменение их формы и/или размеров. Например, из пластилина или глины можно вылепить предмет, форма и размеры которого будут сохраняться и после того, когда мы уберём руки. Такую деформацию называют пластической. Однако, если наши руки деформируют пружину, то когда мы их уберём, возможны два варианта: пружина полностью восстановит форму и размеры или же пружина сохранит остаточную деформацию.

Если тело восстанавливает форму и/или размеры, которые были до деформации, то деформация упругая. Возникающая при этом в теле сила – это сила упругости, подчиняющаяся закону Гука:

F упр – модуль силы упругости тела, Н
| D l| – модуль удлинения тела, м
k – коэффициент жёсткости тела, Н/м

Поскольку удлинение тела входит в закон Гука по модулю, этот закон будет справедлив не только при растяжении, но и при сжатии тел.

Опыты показывают: если удлинение тела мало по сравнению с его длиной, то деформация всегда упругая; если удлинение тела велико по сравнению с его длиной, то деформация, как правило, будет пластической или даже разрушающей. Однако, некоторые тела, например, резинки и пружины деформируются упруго даже при значительных изменениях их длины. На рисунке показано более чем двухкратное удлинение пружины динамометра.

Для выяснения физического смысла коэффициента жёсткости, выразим его из формулы закона. Получим отношение модуля силы упругости к модулю удлинения тела. Вспомним: любое отношение показывает, сколько единиц величины числителя приходится на единицу величины знаменателя. Поэтому коэффициент жёсткости показывает силу, возникающую в упруго деформированном теле при изменении его длины на 1 м.

1. Динамометр является .
2. Благодаря закону Гука в динамометре наблюдается .
3. Явлением деформации тел называют .
4. Пластически деформированным мы назовём тело, .
5. В зависимости от модуля и/или направления приложенной к пружине силы, .
6. Деформацию называют упругой и считают подчиняющейся закону Гука, .
7. Закон Гука носит скалярный характер, так как с его помощью можно определить только .
8. Закон Гука справедлив не только при растяжении, но и при сжатии тел, .
9. Наблюдения и опыты по деформации различных тел показывают, что .
10. Ещё со времени детских игр мы хорошо знаем, что .
11. По сравнению с нулевым штрихом шкалы, то есть недеформированным начальным состоянием, справа .
12. Чтобы понять физический смысл коэффициента жёсткости, .
13. В результате выражения величины «k» мы .
14. Ещё из математики начальной школы мы знаем, что .
15. Физический смысл коэффициента жёсткости состоит в том, что он .

Задача. К пружине, начальная длина которой 10 см, подвесили груз массой 1 кг. При этом пружина удлинилась до 15 см. Определите коэффициент жёсткости для данной пружины. С каким периодом подвешенный груз будет совершать вертикальные колебания на такой пружине?

Решение. Эта задача будет иметь решение, только если мы убедимся, что деформация пружины упруга. То есть при снятии груза пружина должна принять первоначальную длину, равную 10 см. Ответ на этот вопрос даст только опыт, то есть задача – отчасти экспериментальная.

Используя третий закон Ньютона в скалярной форме, а также закон Гука, подсчитаем коэффициент упругости пружины:

F тяж = F упр = k·| D l| = k · |l–l o | = k · ( l–l o )

Подставив жёсткость пружины 200 Н/м в формулу для периода колебаний пружинного маятника (см. § 11-б), вычислим период:

Ответ. Жёсткость пружины равна 200 Н/м, и 10 колебаний маятника будут совершены за 4 секунды, что можно проверить секундомером.

Пока мы вели речь только о твёрдых телах. Однако сила упругости возникает и в жидкостях, и в более сложных телах, например, воздушном шарике, состоящем из резиновой оболочки и воздуха. Можно ли к таким телам применять закон Гука (и если можно, то при насколько больших деформациях), нам даст ответ только эксперимент. Он же позволит вычислить коэффициенты жёсткости для этих тел.

1. Какова длина недеформированной пружины?
2. Чему равно удлинение пружины?
3. В каком случае мы имеем право применить закон Гука?
4. Проверить это можно следующим образом: .
5. Коэффициент жёсткости по результатам вычислений равен .
6. Проверить полученное значение мы можем путём измерения .
7. При проверке нам нужно убедиться, что .
8. Сила упругости возникает не только в .
9. Закон Гука позволяет найти силу упругости .
10. Важно: только предварительный эксперимент по изучению характера деформации позволит нам выяснить, .
11. В случае упругой деформации тел, следующий эксперимент .

Физика.ru • Клуб для учителей физики, учащихся 7-9 классов и их родителей

Измерение параметров жесткости пружин разных типов

При производстве на предприятии и для применения необходимо определить способность пружины выдерживать определенные типы нагрузок. Для этого высчитывается т.н. коэффициент Гука – обозначение жесткости пружины, от которого зависит её надёжность. На этот параметр влияет материал, выбранный для изготовления. Это может быть сталь, легированная кремнием, ванадием, марганцем, другими добавками. Также применяются нержавейка, бериллиевая и кремнемарганцевая бронза, сплавы на основе никеля и титана.

Если деталь выпускается для применения при высоких нагрузках, экстремальных температурах, используются специальные марки легированной стали. Нижегородская метизная корпорация имеет возможность производить пружины под заказ, создавая изделия с заданными характеристиками.

Что такое жесткость?

Говоря о практике, а не физических терминах, это сила, приложив которую, можно сжать пружину. Если вы знаете прилагаемое усилие, можно определить, какой будет деформация, и наоборот. Это существенно облегчает вычисления.

Коэффициент высчитывается для пружин кручения, растяжения, изгиба, сжатия – всех наиболее популярных в промышленности разновидностей этого изделия. Также следует отметить два основных типа:

• С линейной (постоянной) жесткостью;
• С прогрессивной (зависящей от положения витков) жесткостью.

Часто производитель наносит на готовую продукцию пометку краской. Если такого обозначения нет, применяется формула определения жесткости пружины через массу и длину, упрощающая задачу. Она изначально разрабатывалась для пружин растяжения, была получена методом измерения соответствия массы грузы с изменениями геометрии.

Также данный параметр может быть прогрессирующим – растущим — или регрессирующим – убывающим. Во втором случае параметр “жесткости” принято называть “мягкостью”. В отдельных механизмах, например, в автомобилестроении, этот параметр особенно актуален.

Какие вводные данные требуются?

При расчёте важно знать следующую информацию:

• Из какого материала выполнено изделие;
• Точный диаметр витков – Dw;
• Общий диаметр самой пружины – Dm;
• Количество витков – Na.

Таким образом, к коэффициенту жесткости пружинного механизма может применяться формула:

Переменная G означает модуль сдвига. Это значение можно найти в таблицах для разных материалов. К примеру, у пружинной стали G=78,5 ГПа.

Далее разберемся, как определить жесткость пружины по формуле:

Длина L бывает двух типов:

• L1 – измеренная в вертикальном положении без груза;
• L2 – полученная при подвешивании груза с точно известной массой.

Например, 100-граммовая гиря, закреплённая в нижней части, воздействует с силой F, равной 1 Н. Получаем разницу между двумя показателями длины:

При этом следует уточнить, что степень жесткости не определяет распрямление в исходное состояние. На него воздействуют сразу несколько факторов.

Насколько важен показатель, и на что он влияет?

Характеристики пружины важны не только для соответствия ГОСТам и проведения сертификации. Они влияют на сроки эксплуатации изделий, в которых используются, а это огромное количество приборов, деталей, механизмов, от мебели, до различных транспортных средств.

Поэтому данная величина напрямую влияет на надёжность готовых изделий, оборудования, техники, в которых используются элементы, содержащие пружины.

Часто люди интересуются, как рассчитать жесткость пружины цилиндрической винтовой. Для таких случаев учитывается не только модуль сдвига, но и параметр Rs – напряжение, допускаемое при кручении. Здесь в расчёт берётся тип материала, его физические свойства, механические характеристики.

Следующий вопрос – в чем измеряется коэффициент жесткости пружины при расчётах. Традиционно в системе измерений, принятой в нашей стране принято записывать значение в Н/м – ньютонах на один метр. Также это значение в качестве альтернативного варианта может записываться в килограммах на квадратный сантиметр, дин/см, граммах на квадратный сантиметр (расчёты в системе СГС).

В 1635 году родился Роберт Гук, английский физик, член Лондонского королевского общества, его секретарь. В 1660 году открыл закон упругости для твердых тел (закон Гука).

В курсе 7 класса одной из сложных тем является условие равновесия груза на пружине: kx=mg, но предварительно для более эффективного понимания этой темы проводится эксперимент по закону Гука, а затем комментируются формулы: Fу=kx и Fт=mg .

Задачи на данную тему

1) Какова жесткость пружины , если груз массой 10 кг растягивает пружину на 10 см.

2) Используя полученный Ответет из предыдущей задачи определите какой груз нужно подвесить к пружине , чтобы растянуть ее на 20 см.

3) Груз массой 3 кг растягивает пружину на 5 см . Каким должен быть груз , который растянет пружину на 8см.

III. Изучение нового материала:

Вам уже известно, что на все тела, находящиеся на Земле, действует сила тяжести. В результате действия силы тяжести на Землю падает подброшенный камень, выпущенная из лука стрела, снежинки.

Почему же покоятся тела, подвешенные на нити или лежащие на опоре? По-видимому, сила тяжести уравновешивается какой-то другой силой. Что это за сила и как она возникает.

Проведем опыт: на упругий подвес поместим гирю. Под действием силы тяжести гиря начнет двигаться вниз, и подвес деформируется – его длина увеличится. При этом возникнет сила, с которой подвес действует на тело. Когда эта сила уравновесит силу тяжести, тело остановится. Из этого опыта можно сделать вывод, что на гирю, кроме силы тяжести, направленной вертикально вниз, действует другая сила. Эта сила направлена вертикально вверх. Она и уравновешивает силу тяжести. Эту силу называют силой упругости. Аналогичные явления происходят с любым телом которое мы положили на опору.

Ребята, запишите, пожалуйста, в тетрадях определение силы упругости: Сила, возникающая в теле в результате его деформации, и стремящаяся вернуть тело в исходное положение называется силой упругости.

– Проведем эксперимент: линейка и пружина с указателем закреплены на штативе. Будем поочередно подвешивать грузы на пружину и фиксировать ее удлинение. Заносим данные в таблицу . Для расчета силы упругости используем равенство сил, действующих на груз: Fупр = Fтяж = mg. По данным таблицы строим график зависимости Fупр(∆l).

– Какую линию получили на графике?

– Как называется такая зависимость в математике?

– Что происходит с силой упругости, если длина пружины увеличивается? Уменьшается?

– Как изменится сила упругости, если длина пружины увеличится в 2 раза? Посмотрим на график.

– Найдем отношение силы упругости к удлинению пружины (первый результат считаю я, остальные вы – по вариантам):

– Какой вывод можно сделать об отношении силы упругости к удлинению пружины?

– Мы с вами получили закон, открытый английским физиком Робертом Гуком в 1660г.

– Закон Гука: Fупр = k∆l – сила упругости прямо пропорциональна величине деформации. Обсудим формулу закона и попытаемся определить, какие величины в нее входят (обсуждение формулы, записи величин и единиц их измерения).

Теперь мы можем написать условие равновесия груза на пружине : mg = k∆l , используем это условие при решении задачи №1:

1) Какова жесткость пружины , если груз массой 10 кг растягивает пружину на 0,1 м.

М=10кг
L=0,1м
k-?

Решение:

mg = k∆l
mg : ∆l = k

После подстановки получаем ответ: 1000Н/м

Теперь зная жесткость пружины, разберем ситуацию каким образом мы можем узнать массу тела, рассмотрим задачу №2:

2) Используя полученный ответ из предыдущей задачи определите какой груз нужно подвесить к пружине, чтобы растянуть ее на 20 см.

k =1000Н/м
L=0,2м
М – ?

Решение:

mg = k ∆l
m = k ∆l:g

После подстановки получаем ответ: 20 кг

А теперь используем наши умения и навыки для решения более сложной задачи:

3) Груз массой 3 кг растягивает пружину на 5 см. Каким должен быть груз, который растянет пружину на 8см.

М1=3кг
L1=0,05м
L2=0,08м
М2=?

Решение:

М1 g = k L1
М1 g : L1 = k =600 Н/м

Нашли жесткость, теперь можем написать условие равновесия груза на пружине и найти массу груза:

Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.

Виды деформации

Деформация – это изменение формы, или размеров тела.

Есть несколько видов деформации:

• сдвиг;
• кручение;
• изгиб;
• сжатие/растяжение;

Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.

Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.

Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.

В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.

Растяжение пружины

Рассмотрим подробнее деформацию растяжения на примере пружины.

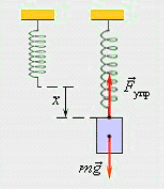
Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина (L_{0}) пружины.

Подвесим теперь к пружине груз. Пружина будет иметь длину (L), указанную на рисунке справа.

Сравним длину нагруженной пружины с длиной свободно висящей пружины.

[ large L_{0} + Delta L = L ]

Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину (L_{0}).

[ large boxed{ Delta L = L — L_{0} }]

( L_{0} left(text{м} right) )  – начальная длина пружины;

( L left(text{м} right) )  – конечная длина растянутой пружины;

( Delta L left(text{м} right) )  – кусочек длины, на который растянули пружину;

Величину ( Delta L ) называют удлинением пружины.

Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.

Примечание: Отношение – это дробь. Относительное – значит, дробное.

[ large boxed{ frac{Delta L }{ L_{0}} = frac{ L — L_{0}}{L_{0} } = varepsilon } ]

( varepsilon ) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.

Расчет силы упругости

Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.

Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.

Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.

Закон Гука

Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.

[ large boxed{ F_{text{упр}} = k cdot Delta L }]

Эту формулу назвали законом упругости Гука.

( F_{text{упр}} left( H right) ) – сила упругости;

( Delta L left(text{м} right) )  – удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) )  – коэффициент жесткости (упругости).

Какие деформации называют малыми

Закон Гука применяют для малых удлинений (деформаций).

Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.

Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.

Как рассчитать коэффициент жесткости

Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.

Так как силы взаимно компенсируются, в правой части уравнения находится ноль.

[ large F_{text{упр}} — m cdot g = 0 ]

Подставим в это уравнение выражение для силы упругости

[ large k cdot Delta L — m cdot g = 0 ]

Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:

[ large boxed{ k = frac{ m cdot g }{Delta L} }]

(g) – ускорение свободного падения, оно связано с силой тяжести.

Соединяем две одинаковые пружины

В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.

Параллельное соединение пружин

На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.

Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).

Одна пружина:

[ large k_{1} cdot Delta L = m cdot g ]

Две параллельные пружины:

[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]

Так как правые части уравнений совпадают, левые части тоже будут равны:

[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]

Умножим обе части полученного уравнения на число 2:

[ large boxed{ k_{text{параллел}} = 2k_{1} } ]

Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной

Последовательное соединение пружин

Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.

Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.

На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).

Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений

Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).

Одна пружина:

[ large k_{1} cdot Delta L = m cdot g ]

Две последовательные пружины:

[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]

Так как правые части уравнений совпадают, левые части тоже будут равны:

[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

[ large k_{text{послед}} cdot 2 = k_{1} ]

Разделим обе части полученного уравнения на число 2:

[ large boxed{ k_{text{послед}} = frac{k_{1}}{2} } ]

Коэффициент жесткости (k_{text{послед}}) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной

Потенциальная энергия сжатой или растянутой пружины

Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу,  например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.

Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).

Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:

[ large boxed{ E_{p} = frac{k}{2} cdot  left( Delta L right)^{2} }]

( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;

( Delta L left(text{м} right) )  – удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) )  – коэффициент жесткости (упругости) пружины.

Выводы

1. Упругие тела – такие, которые сопротивляются деформации;
2. Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
3. Деформация – изменение формы, или размеров тела;
4. Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
5. Удлинение пружины – это разность ее конечной и начальной длин;
6. Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
7. Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
8. Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
9. А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.

Как найти длину пружины

Длина проволоки, из которой свита пружина, значительно больше длины самой пружины. Чтобы узнать протяженность этой проволоки, необязательно портить пружину, разматывая ее. Достаточно осуществить расчет.

Вам понадобится

• – пружина;
• – штангенциркуль;
• – тиски;
• – защитные перчатки;
• – защитные очки;
• – калькулятор.

Инструкция

Измерьте диаметр пружины в сжатом состоянии при помощи штангенциркуля. Не прилагайте к ней при этом значительных усилий, иначе она сожмется, что исказит результат измерения в сторону уменьшения. Лучше всего измерить диаметр в нескольких местах, после чего найти среднее арифметическое результатов измерения по следующей формуле:D=(D1+D2+D3+…+Dn)/n, где D – средний диаметр, мм, D1…Dn – результаты измерений, мм, n -количество измерений (безразмерная величина).

Найдите длину окружности одного витка по следующей формуле:l=πD, где l – длина окружности в мм, π – число «пи», D – диаметр одного витка (мм).На самом деле виток имеет форму не окружности, а овала (за счет того, что сама проволока обладает ненулевым диаметров, и каждый виток даже в сжатом состоянии имеет диагональное продольное сечение), но удлинение за счет этого столь незначительно, что им можно пренебречь.

Сосчитайте количество витков пружины (обязательно в полностью разжатом состоянии). Чтобы не ошибиться, можно использовать при подсчете витков упругую полоску, например, из гибкой пластмассы. При каждом перескакивании с витка на виток она будет издавать отчетливый щелчок. Достаточно сосчитать количество этих щелчков и прибавить к ним единицу (с последнего витка полоска соскочит почти беззвучно, поскольку не ударится о следующий).

Умножьте длину окружности одного витка пружины на число витков:L=lN, где L – длина проволоки, из которой свита пружина, мм, l – длина окружности одного витка, мм, N – количество витков пружины (безразмерная величина).

Обратите внимание

При необходимости используйте защитные перчатки. Сжимайте и разжимайте пружину не резко, а плавно. Защищайте глаза.

Полезный совет

Сжимая сильную пружину, будьте осторожны – она может выскользнуть и причинить травмы. Очень сильные пружины лучше измерять в разжатом или слегка сжатом состоянии, несмотря на то, что точность при этом несколько уменьшится. Особенно осторожным нужно быть, если для сжатия используются тиски или другие механические приспособления.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?