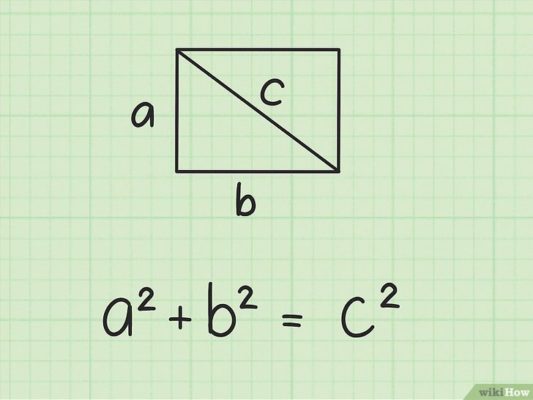If you know the length and width of a rectangle, you can figure out its area. These two quantities are independent, though, so you can’t do a reverse calculation and determine both of them if you know only the area. You can calculate one if you know the other, and you can find both of them in the special case in which they are equal – which makes the shape a square. If you also know the perimeter of the rectangle, you can use that information to find two possible values for length and width.
Determining Length or Width When You Know the Other
The area of a rectangle (A) is related to the length (L) and width (W) of its sides by the following relationship:
A = L × W
If you know the width, it’s easy to find the length by rearranging this equation to get
L = frac{A}{W}
If you know the length and want the width, rearrange to get
W = frac{A}{L}
Example: The area of a rectangle is 20 square meters, and its width is 3 meters. How long is it?
Using the expression
W = frac{A}{L}
you get
W = frac{20 text{ m}^2}{3 text{ m}} = 6.67 text{ m}
The Square, a Special Case
Because a square has four sides of equal length, the area is given by A = L2. If you know the area, you can immediately determine the length of each side, because it’s the square root of the area.
Example: What are the lengths of the sides of a square with an area of 20 m2?
The length of each side of the square is the square root of 20, which is 4.47 meters.
Finding Length and Width When You Know Area and Perimeter
If you happen to know the distance around the rectangle, which is its perimeter, you can solve a pair of equations for L and W. The first equation is that for area,
A = L × W
and the second is that for perimeter,
P = 2L + 2W
To solve for one of the variables – say W – you have to eliminate the other.
Since P = 2L + 2W, you can write
W = frac{P – 2L}{2}
You know A = L × W, so
W = frac{A}{L}
Substituting for W, you get:
frac{P – 2L}{2} = frac{A}{L}
Multiply both sides by L to eliminate the fraction, and you get this equation:
2L^2 – PL + 2A = 0
This is a quadratic equation, which means it has two solutions derived from the standard formula for solving these equations: The solutions are
L = frac{P + sqrt{P^2 – 8A}}{2} text{ and } L = frac{P – sqrt{P^2 – 8A}}{2}
Knowing the perimeter may not give you a unique answer, but two answers are better than none.
Как найти длину, если известна площадь и ширина
При решении геометрических задач обычно рассчитываются одни параметры, если известны другие. Например, если заданы площадь и ширина прямоугольника, то можно найти его длину. Аналогичные задачи нередко приходится решать и на практике – при измерениях или планировке жилплощади, земельных участков или покупке стройматериалов.
Вам понадобится
- калькулятор
Инструкция
Чтобы найти длину стороны прямоугольника, если известна ширина и площадь, разделите числовое значение площади на числовое значение ширины. То есть воспользуйтесь формулой:Д = П / Ш, где:Д – длина стороны прямоугольника,
Ш – ширина прямоугольника,
П – его площадь.Например, если площадь прямоугольника равна 20 см², а его ширина – 5 см, то длина его стороны будет: 20 / 5 = 4 см.
Перед началом вычислений переведите ширину и площадь прямоугольника в одну систему измерений. То есть, площадь должна выражаться в соответствующих ширине квадратных единицах измерения. При этом, длина получится в тех же единицах, что и ширина. Так, если ширина задана в метрах, то площадь необходимо перевести в метры квадратные. Особенно актуален такой перевод при измерении земельных участков, где площадь обычно задана в гектарах, арах и «сотках».
Например, пусть площадь дачного участка равняется шести соткам, а его ширина – 30 метров. Требуется найти длину участка.
Так как «соткой» называют 100 квадратных метров, то площадь «стандартных» шести соток можно записать как 600 м². Отсюда длину земельного участка можно найти разделив 600 на 30. Получается – 20 метров.
Иногда заданы площадь и ширина фигуры, имеющей не прямоугольную, а произвольную форму. При этом, также требуется найти ее длину. Как правило, в это случае подразумеваются габаритные размеры фигуры, то есть параметры прямоугольника, в который эту фигуру можно заключить.
Если большая точность вычислений не требуется, то воспользуйтесь вышеприведенной формулой (Д = П / Ш). Однако, значение длины при этом получится заниженным. Чтобы получить более точное значение длины фигуры, оцените насколько полно фигура заполняет свой габаритный прямоугольник и разделите полученную длину на коэффициент заполнения.
Так, например, если озеро имеет площадь 100 квадратных километров, его ширина равна 5 километров и оно занимает примерно половину габаритного прямоугольника, то его длина будет: 100 / 5 / 0,5 = 40 километров.
Источники:
- Какова длина прямоугольника, если известна его ширина
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Длина прямоугольника

4.6
Средняя оценка: 4.6
Всего получено оценок: 89.
4.6
Средняя оценка: 4.6
Всего получено оценок: 89.
В этой статье мы поговорим о длине прямоугольника. Как определить, какая из сторон является длиной и зачем их разделять. Разберем три способа нахождения длины прямоугольника и решим небольшую задачу.
Опыт работы учителем математики – более 33 лет.
Что такое длина прямоугольника
Довольно часто люди путают местами длину и ширину прямоугольника, как правило, это не критично, но в результате значительно уменьшается наглядность, а от этого страдает качество решения.
Прямоугольник это частный случай параллелограмма. Параллелограмм, каждый угол которого равен 90 градусам, называется прямоугольником. Для наглядного изображения лучше будет, если нижней опорой прямоугольника будет служить длина. Так сложилось, что такой рисунок больше всего напоминает рисунки в учебнике, а потому ученику будет проще разобраться в теме.
Три способа найти длину прямоугольника
Если разделить фигуру на две части диагональю, то можно заметить, что прямоугольник поделится ею на два прямоугольных треугольника. Из этого разделения и вытекают все формулы длины прямоугольника.
-
Через теорему Пифагора
Если известна длина диагонали (обозначим ее буквой d) и длина прямоугольника (примем значение за букву a). Тогда корень квадратный из разности квадратов диагонали и длины будет равен ширине прямоугольника.
Чтобы было понятнее, напишем решение в виде нескольких формул.
Согласно теореме Пифагора – квадрат гипотенузы равен сумме квадратов катетов. Гипотенуза – это сторона, противоположная прямому углу, две другие стороны зовутся катетами. В нашем случае гипотенуза это диагональ.
Значит: d2=a2+b2 . Из этого выражения выразим квадрат ширины (значение «b»):b2=d2-a2
Для того, чтобы определить значение b, нужно взять корень квадратный из обеих сторон получившегося выражения: b=(d2-a2)(-1)
В случае необходимости, можно поменять местами а и b, тогда получится формула длины.
-
Через площадь
Рассмотрим еще один способ найти длину прямоугольника – через площадь.Площадь прямоугольника равна произведению длины и ширины. То есть, используя уже знакомые обозначения S=a*b. Выразим из этой формулы значение ширины: b=S/b.
Так же, как и в первом методе, можно поменять местами а и b, чтобы получить формулу для длины: a=S/b.
-
Тригонометрическая функция
Один из самых быстрых, но при этом немного сложных способов нахождения длины – воспользоваться тригонометрической функцией.
Если имеется прямоугольный треугольник, то соответственно имеются отношения, известные как синус и косинус.
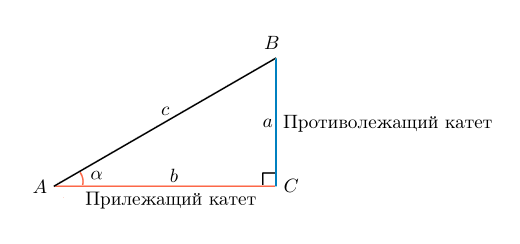
Выберем угол между длиной и диагональю. Обозначим его α. Тогда sin α равен отношению катета, противоположного углу α к гипотенузе: Sin α = a/c
Значение синуса любого угла можно найти в таблицах Брадиса или с помощью калькулятора. Для удобства можно воспользоваться онлайн-версией, которая найдет значение отношения автоматически.
Но в формуле нет значения b, которое соответствует длине, а, значит, воспользуемся основным тригонометрическим тождеством. Косинус – это отношение стороны, прилежащей к углу, к гипотенузе: cos a=b/c
Значит можно найти длину, умножив косинус на гипотенузу: b=cos α*c
Задача
- Найти длину прямоугольника, если известно, что его ширина равна 3, а диагональ 5.
Воспользуемся теоремой Пифагора и найдем b. Длина равна корню квадратному из разности квадрата диагонали и квадрата ширины.
5^2=25
3^2=9
25-9=16
Корень квадратный из 16 равен 4.
Значение b=4
Что мы узнали?
Мы рассмотрели, как правильно изображать прямоугольник для большей наглядности, рассмотрели как можно найти длину или ширину при различных условиях задачи и решили задачу средней сложности на нахождение длины прямоугольника через теорему Пифагора.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 89.
А какая ваша оценка?
Как найти длину и ширину прямоугольника если известна его площадь
Ширину можно вычислить по длине, если известна еще площадь или периметр прямоугольника. Например, зная площадь и длину, можно найти ширину по формуле а = S/b. А зная периметр и длину, можно вычислить ширину по формуле a = (P — 2b) / 2.
- Ширина прямоугольника может быть найдена по длине и площади или по длине и периметру.
- Для нахождения ширины по длине и площади используется формула а = S/b.
- Для нахождения ширины по длине и периметру используется формула a = (P — 2b) / 2.
- Если известна только площадь прямоугольника, а одна из его сторон, то другая сторона может быть найдена по формуле а = S: b.
- Для нахождения длины и ширины по площади фигуры необходимо умножить их друг на друга: S = a × b.
- Чтобы найти длину и периметр прямоугольника, необходимо разделить площадь на ширину, затем прибавить ширину к длине и умножить на два.
- Для нахождения длины прямоугольника необходимо из периметра вычесть две ширины и результат разделить на два.
- Длину стороны прямоугольника можно выразить через периметр и ширину по формуле а = (P — 2b): 2.
- Чтобы найти длины сторон прямоугольника по его площади и периметру, необходимо решить систему двух уравнений.
- Длина предмета определяется в продольном направлении, а ширина — в поперечном направлении. Длиной является самый большой размер, а шириной — размер поменьше.
- Как найти длину сторон прямоугольника если известна только площадь
- Как найти длину и ширину по площади
- Как найти длину и периметр если известна площадь и ширина
- Как узнать длину и ширину прямоугольника если известен периметр
- Как найти длину прямоугольника
- Как узнать длину стороны прямоугольника
- Как найти длину стороны по площади
- Как определить длину и ширину
- Как найти ширину прямоугольника
- Как найти периметр прямоугольника зная его площадь
- Как найти длину прямоугольника формула 4 класс
- Где длина и ширина прямоугольника
- Как найти сторону треугольника если известна его площадь
- Как найти боковые стороны прямоугольника
- Как найти стороны прямоугольника зная его периметр
- Как найти сторону прямоугольника зная его периметр
Как найти длину сторон прямоугольника если известна только площадь
Если известна площадь прямоугольника, и одна из сторон прямоугольника: а = S: b, где S — площадь прямоугольника, b — сторона прямоугольника.
Как найти длину и ширину по площади
Когда известно значение длины и ширины фигуры
Для вычисления необходимо умножить их друг на друга. S = a × b, где S — площадь; a, b — длина и ширина.
Как найти длину и периметр если известна площадь и ширина
Надо площадь разделить на длину потом к длине прибавить ширину и умножить на два.
Как узнать длину и ширину прямоугольника если известен периметр
1. Периметр прямоугольника находится по формуле Р = 2 * (а + b), где Р — периметр, а — длина, b — ширина. Выведем из этой формулы формулу ширины: b = Р / 2 — а.
Как найти длину прямоугольника
Для того, чтобы найти длину этого прямоугольника нужно из данной величины периметра вычесть две ширины прямоугольника и полученный результат разделить на два.
Как узнать длину стороны прямоугольника
P = a + b + a + b = 2a + 2b. Отсюда можно выразить длину стороны а: 2а = P — 2b; а = (P — 2b): 2.
Как найти длину стороны по площади
Для того, чтобы найти длины сторон прямоугольника зная его площадь (S = a * b) и периметр (P = 2(a + b)) составим и решим систему двух уравнений.
Как определить длину и ширину
Длина предмета находится в продольном направлении, а его ширина — размещается поперек длины. Таким образом, длиной предмета будет самый большой его размер, а шириной — размер поменьше.
Как найти ширину прямоугольника
Определение прямоугольника
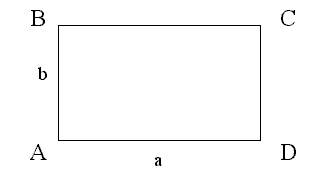
Длинную сторону прямоугольника называют длиной (обозначается латинской буквой — a), а короткую — шириной (обозначается латинской буквой — b). Стороны прямоугольника одновременно является его высотами (см. Рис. 1).
Как найти периметр прямоугольника зная его площадь
Поделите площадь на длину известной стороны. Прибавьте результат к известной стороне. Умножьте полученное число на два.Умножьте полученное число на два:
- P — искомый периметр прямоугольника;
- a — известная сторона;
- S — площадь прямоугольника.
Как найти длину прямоугольника формула 4 класс
Найдём длину прямоугольника исходя из формулы периметра. Р = (а + b) * 2, где а — ширина, b — длина прямоугольника. Подставим в нашу формулу известные ширину и периметр.
Где длина и ширина прямоугольника
Противоположные стороны прямоугольника равны. Длинную сторону прямоугольника называют длиной прямоугольника, а короткую — шириной прямоугольника.
Как найти сторону треугольника если известна его площадь
Из формулы площади находим квадрат стороны треугольника. a^2 = 4 * S: √3. Затем находим сторону треугольника. a = √(4 * S: √3).
Как найти боковые стороны прямоугольника
Ответы1:
- Периметр нашего прямоугольника делим на 2.
- Выражаем одну из сторон прямоугольника.
- Составляем уравнение с двумя неизвестными по теореме Пифагора, где нашу диагональ возводим в квадрат.
- Подставляем нашу сторону, которую мы выражали раннее во вторую формулу.
- Через дискриминант находим ответ.
Как найти стороны прямоугольника зная его периметр
Если известен периметр и одна из сторон прямоугольника, допусти В, находим из формулы сторону А: 2А = Р — 2В; А = (Р — 2В) / 2.
Как найти сторону прямоугольника зная его периметр
1) Формула нахождения периметра прямоугольника имеет вид: S = 2(a + b), где а и b — это стороны прямоугольника.
Оставить отзыв (1)
|
Площадь – 56 квадратных см. Периметр – 30 см. Сторона А=7, сторона В=8 S=AxB P=2A+2B S=56 P=30 автор вопроса выбрал этот ответ лучшим Можно попробовать решить данную задачу, составив систему уравнений. Периметр прямоугольника равен: p=2a+2b; Площадь прямоугольника равна: s=a*b; Так как мы знаем периметр и площадь, то сразу подставляем числа: 30=2a+2b; 56=a*b; Выражаем b через a во втором уравнении: b=56/a; И подставляем 56/a вместо b в первое уравнение: 30=2a+2(56/a); 15=a+56/a; Домножаем обе части на a: 15a=a²+56; Получаем квадратное уравнение: a²-15a+56=0; Находим корни этого квадратного уравнения: (15±√(15²-4*1*56))/2*1 = (15±√(225-224))/2 = (15±√1)/2 = (15±1)/2 Получилось, что корни этого уравнения: a1=(15+1)/2=16/2=8; a2=(15-1)/2=14/2=7; Получается, что у нас 2 возможных варианта прямоугольников. Вспомним, что мы выразили: b=56/a; Отсюда находим возможные b: b1=56/a1=56/8=7; b2=56/a2=56/7=8; Как оказалось эти два разных прямоугольника – это один и тот же, просто достигнуть периметра в 30 при площади в 56 можно: Если a=7 и b=8. Либо наоборот: a=8 и b=7. То есть в сущности у нас один и тот же прямоугольник, просто в одном варианте вертикальная сторона больше горизонтальной, а в другом наоборот – горизонтальная больше вертикальной. Ответ: одна сторона 7 сантиметров, а вторая 8 сантиметров.Oleg74 9 лет назад Если периметр прямоугольника Р = 30 см, а его площадь S = 56 см, то его стороны будут равны : а – одна сторона, в – другая сторона прямоугольника. S = а * в P = 2а + 2в Решив эту систему, приходим к тому, что сторона а будет равна 7 см, а сторона в будет равна 8 см. а = 7 см в = 8 см. Чтобы решить поставленную задачу, нужно составить систему уравнений и решить ее S = а*b P = 2(а+b) получим квадратное уравнение, которое легко решается, если подставить в него значения периметра и площади Дискриминант равен 1 и уравнение имеет два корня 7 и 8, следовательно одна из сторон равна 7 см, другая 8 см или наоборот. Я специально выписал здесь дискриминант, так как по нему очень хорошо ориентироваться если в условии задачи на нахождение сторон прямоугольника значение периметра и площади заданы так, что этот дискриминант больше ноля, тогда мы имеем прямоугольник; если дискриминант равен нолю – тогда имеем квадрат (P=30, S=56,25, квадрат со стороной 7,5); если дискриминант меньше ноля, то тогда такой прямоугольник не существует (P=20, S=56 – решения нет) Galina7v7 7 лет назад Дано: S = 56 смР = 30 смСтороны=?Решение:Пусть стороны прямоугольника a и b. Тогда: площадь S = a * b , периметр Р=2*(a + b), Получим систему уравнений: {a*b=56 ? {ab=56 {2(a+b)=30, {a+b=15 ,выражая b через а получим квадратное уравнение: b=15-a, a^2 -15a +56 =0 ,решая которое ,получим : a1=7, a2=8, b1=8, b2=7. То есть стороны прямоугольника: a=7,b=8 ,или наоборот:a=8,b=7. Zolotynka 7 лет назад Нашла еще такое решение, Известно, что периметр прямоугольника 30 а площадь 56, далее: периметр = 2*(длина + ширина) или 2L + 2W площадь= длина * ширина или L * W 2L + 2W = 30 (делим обе части на 2) L + W = 15 L * W = 56 L * (15 – L) = 56 Честно говоря, не совсем поняла решение, но думаю, тот, кто не совсем подзабыл математику, разберется. Azamatik 7 лет назад Вспоминаем школьную геометрию: Периметр прямоугольника – это будет сумма длин всех сторон, а площадь прямоугольника – это уже произведение двух смежных его сторон (длину на ширину). В данном случае нам известны и Площадь и Периметр прямоугольника. Они равны 56 см^2 и 30 см соответственно. Итак, решение: S – площадь = а x b; 56 = a x b; Р – периметр = а + b + a + b = 2a + 2b; 30 = 2 (а + b); 15 = a + b; a = 15 – b; Делаем подставление: 56 = (15 – b) x b; 56 = 15 b – b^2; b^2 – 15b + 56 = 0. Получили квадратное уравнение, решая которое получаем: b1 = 8, b2 = 7. Находим и другую сторону прямоугольника: a1 = 15 – 8 = 7; a2 = 15 – 7 = 8. Ответ: стороны прямоугольника равны 8 и 7 см или же 7 и 8 см. Зная формулы периметра прямоугольника и его площади, стороны ищутся в виде решения системы двух уравнений. Для начала выражаем значение одной стороны через другую и например площадь.Это выглядит так А=S/В=56/В Затем подставляем это выражение вместо буквы А в уравнении для периметра: Р=2(56/В + В)=30 Получаем что 56/В+В=15 В этом уравнении даже решать его не надо – любому человеку знакомому с таблицей умножения сразу видно, что 56 это произведение 7 и 8, а поскольку и сумма этих цифр как раз 15, то они и есть нужные нам значения сторон прямоугольника. Хеленочка 8 лет назад Обозначим одну сторону буквой Х, другую – буквой Y. Площадь прямоугольника вычисляется умножением длин сторон, следовательно, мы можем составить первое уравнение: Х*Y=56 Периметр – это сумма длин сторон, следовательно, второе уравнение такое: 2Х+2Y=30 Получаем систему двух уравнений. По первому уравнению выделяем Х: Х=56:Y, подставляем это во второе уравнение: 2*56:Y+2Y=30 Отсюда уже легко найти значение Y: Y=7, тогда Х=8. Lilechka 9 лет назад Периметр 30, площадь 56. Назовем стороны прямоугольника а и с. Тогда можем составить такие уравнения: (а+c)х2=30 ахс=56 Далее решаем систему уравнений и находим, что стороны прямоугольника составляют 7 и 8 см. moreljuba 7 лет назад Итак, для начала рассмотрим формулы для нахождения площади и периметра: 1) S = a * b = 56 см2; 2) Р = 2а + 2b = 30 см. Ведь мы знаем, что прямоугольник имеет по две одинаковых стороны. Таким образом нам требуется решить систему из двух уравнений: a * b = 56 2а + 2b = 30 Отсюда получаем, что одна сторона равна 7, а другая 8. Знаете ответ? |