Как найти длину прямоугольного параллелепипеда 5 класс

Математика

5 класс

Урок №31

Прямоугольный параллелепипед

Перечень рассматриваемых вопросов:

– куб;

– параллелепипед;

– элементы параллелепипеда;

– развёртка параллелепипеда.

Тезаурус

Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками.

Грань – плоская поверхность предмета, составляющая угол с другой такой же поверхностью.

Основания параллелепипеда – это его верхняя и нижняя грани.

Обязательная литература

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений.// С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 класс. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Мир, в котором мы живём, состоит из огромного количества разных по форме, цвету и размеру предметов. Изучая их свойства, люди открывают что-то новое. Например, математики в окружающем пространстве обращают внимание на геометрические тела: цилиндры, кубы и так далее.

Сегодня мы рассмотрим прямоугольный параллелепипед – многогранник, название которого с древнегреческого переводится как «идущие рядом плоскости».

Прямоугольный параллелепипед ограничен шестью прямоугольниками, то есть шестью гранями. Грань, на которую поставлен параллелепипед, и ей противоположную называют нижним и верхним основаниями.

Остальные четыре грани называют боковыми гранями.

Стороны граней параллелепипеда называют рёбрами. Их двенадцать.

Концы рёбер называют вершинами. Их в параллелепипеде восемь.

Каждая вершина является общим концом трёх рёбер.

Длины двух рёбер основания, выходящих из одной вершины, называют длиной и шириной прямоугольного параллелепипеда.

Длину бокового ребра называют высотой.

Таким образом, длины трёх рёбер, выходящих из одной вершины, называют длиной, шириной, высотой. Иначе длину, ширину и высоту называют измерениями прямоугольного параллелепипеда.

Прямоугольный параллелепипед, у которого три ребра, выходящие из одной вершины, равны между собой, называется кубом. Каждая грань куба – квадрат.

Рассмотрим свойства прямоугольного параллелепипеда и куба.

У прямоугольного параллелепипеда противоположные грани равны.

Все грани куба равны между собой.

Построим прямоугольник заданной длины а и высоты h.

Для этого от каждой вершины отложим отрезок, равный половине ширины b под углом 45 градусов. И соединим концы отрезков, причём невидимые грани – пунктирной линией.

Изготовить параллелепипед можно несколькими способами. Например, с помощью развёртки. Для этого на бумаге вычерчивается макет, который выглядит как приведённый шаблон. Обратите внимание, что на картинке даны припуски для того, чтобы можно было склеить параллелепипед.

Другой способ изготовления параллелепипеда – модульная сборка. Она требует ряда последовательных действий.

1) Вырежьте из бумаги шесть одинаковых квадратов.

2) Согните их к середине, как показано на картинке.

3) Согните верхние и нижние края заготовки, как показано на рисунке.

4) Верхний уголок опустите вниз, а нижний – загните наверх. После этого получится квадрат.

5) Сделайте шесть таких заготовок и соедините их в один параллелепипед. Для этого каждый острый уголок вставьте в кармашек соседней части кубика.

Тренировочные задания

№ 1. Какова площадь верхней грани параллелепипеда?

S = ___ см²

Решение: площадь верхней грани параллелепипеда соответствует площади прямоугольника. Верхняя грань параллелепипеда имеет длину 15см и ширину 3см. Значит, далее по формуле вычисляем площадь:

S = а ·b = 15 см · 3 см = 45 см²

Ответ: 45 см²

№ 2. На рисунке изображен куб, состоящий из нескольких маленьких кубиков. Сколько маленьких кубиков ушло на построение данного куба?

Решение: для решения задачи нужно посмотреть, сколько маленьких кубиков расположено на одной грани куба. Их 9 штук. Всего на рисунке изображено три грани. Таким образом, чтобы найти общее количество маленьких кубиков, следует умножить количество кубиков, умещающихся на одной грани, на количество граней: 9 · 3= 27 штук.

Ответ: 27 штук.

Ответ или решение 2

1) Сначала запишем формулу нахождения объёма прямоугольного параллелепипеда:

V = a × b × h, где а — длина, b — ширина, h — высота.

2) Из формулы нахождения объёма парвллелепипеда выразим формулу нахождения длины:

Объём параллелепипеда 40 м.куб. Высота равна 4 м, ширина 2 м. Найдите длину параллелепипеда.

40 : 4 : 2 = 5 (м) — длина параллелепипеда.

Прямоугольный параллелепипед — пространственная фигура с шестью гранями, каждая из которых является прямоугольником. Противолежащие грани параллелепипеда равны.

По условию задан прямоугольный параллелепипед со следующими параметрами:

Объём прямоугольного параллелепипеда

Объём прямоугольного параллелепипеда V вычисляется как произведение площади основания многогранника и его высоты.

Площадь основания, которая представляет собой прямоугольник, выражается как произведение его длины и ширины, то есть

S (основания) = а * b.

Соответственно, V (прямоугольного параллелепипеда) = S (основания) * h = а * b * h.

Объём прямоугольного параллелепипеда равен произведению всех его параметров: высоты, ширины и длины.

Длина прямоугольного параллелепипеда

Таким образом, из приведенной выше зависимости можно выразить длину прямоугольного параллелепипеда:

Итак, длина прямоугольного параллелепипеда равна отношению его объема к произведению ширины и высоты.

Ответ

Проверено экспертом

Ответ:

Объем = длина * ширина * высота

длина = объем : (ширина * высота)

Пошаговое объяснение:

• Комментарии (2)
• Отметить нарушение

Ответ

Чтобы найти объем прямоугольного параллелепипеда, нужно умножить длину, ширину и высоту. Пример: Длина прямоугольного параллелепипеда равна 5 см, ширина — 10 см, а высота — 4 см, то объем такого прямоугольного параллелепипеда будет равен 4*5*10=200 см куб.

Объем прямоугольного параллелепипеда, формула.

Параллелепипедом является призма, основание у которой – это параллелограмм. У параллелепипеда

6 граней, а они, в свою очередь, являются параллелограммами.

Параллелепипед, у которого 4 боковые грани — это прямоугольники, является прямым

Прямой параллелепипед, у которого все 6 граней прямоугольники, является прямоугольным.

Другими словами, прямоугольный параллелепипед — это объемная фигура, у которой есть 6 граней, и

Объем прямоугольного параллелепипеда равен произведению площади основания на высоту:

где, H — высота параллелепипеда,

a – длина параллелепипеда,

b – ширина параллелепипеда,

h — высота прямоугольного параллелепипеда,

Примеры прямоугольного параллелепипеда: спортивный зал, кирпич, картонная коробка или столешница

Длины 3 рёбер прямоугольного параллелепипеда, которые имеют общий конец, называются измерениями

прямоугольного параллелепипеда.

Прямоугольный параллелепипед с одинаковыми измерениями является кубом. Все 6 граней куба — это

Квадрат длины диагонали прямоугольного параллелепипеда = сумме квадратов 3 его измерений.

Объем прямого параллелепипеда, формула.

Как найти объем параллелепипеда?

Площадь боковой поверхности параллелепипеда, формула:

где Р_о — периметр основания,

Площадь полной поверхности, формула

где S_о — площадь основания

Формула объёма прямого параллелепипеда:

Объем произвольного параллелепипеда.

Объём и соотношения в наклонном параллелепипеде часто определяются с помощью векторной алгебры.

Чему равен объём параллелепипеда? Объем параллелепипеда равен абсолютной величине смешанного

произведения трёх векторов, которые определяются 3-мя сторонами параллелепипеда, которые исходят

из одной вершины.

Соотношение длина сторон параллелепипеда – угол между ними даёт утверждение, что определитель

Грама указанных 3х векторов равен квадрату их смешанного произведения.

Представление о том, что такое прямоугольный параллелепипед, все имеют еще с детства, когда играли в кубики, держали в руках такие предметы, как коробка из-под сока или из- под конфет, видели аквариум такой формы. В жизни мы постоянно сталкиваемся с предметами, которые представляют собой прямоугольный параллелепипед (рисунок 1).

Определение

Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками. Грань – плоская поверхность предмета, составляющая угол с другой такой же поверхностью. Основания параллелепипеда – это его верхняя и нижняя грани.

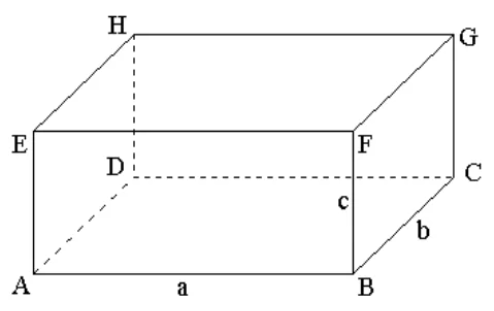
Так, на рисунке 2 показан прямоугольный параллелепипед ABCDEFGH. Он имеет 6 граней, основаниями являются грани ABCD и EFGH.

У параллелепипеда есть вершины, их 8. Они обозначены заглавными латинскими буквами. Также у прямоугольного параллелепипеда есть 12 ребер – это стороны граней: AB, BC, CD, AD, EF, FG, HG, EH, AE, BF, CG, HD.

Противоположные (не имеющие общих вершин) грани прямоугольного параллелепипеда равны.

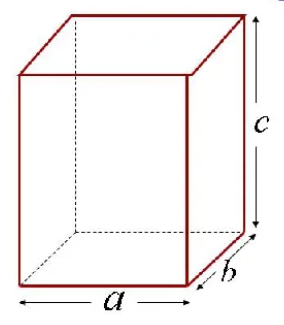
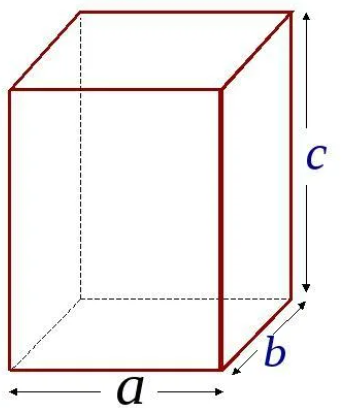
Длина, ширина, высота

Прямоугольный параллелепипед имеет три измерения – длину (а), ширину (b) и высоту (c) – рисунок 3. Зная эти измерения, можно найти не только площадь каждой грани, но и площадь всей поверхности прямоугольного параллелепипеда.

Так как каждая грань параллелепипеда – это прямоугольник, то для нахождения площади любой грани надо умножить длину и ширину этих граней, т.е S=ab, S=bc, S=ac.

Для нахождения площади поверхности прямоугольного параллелепипеда надо сложить площади всех граней, то есть S поверхности = ab+bc+ac+ab+bc+ac. Так как противоположные грани равны, то их площади тоже равны, значит S поверхности = 2ab+2bc+2ac. Это действие можно записать короче, вынося 2 за скобки, как общий множитель, то есть S поверхности = 2(ab+bc+ac). Таким образом, нахождение площади поверхности становится более быстрым.

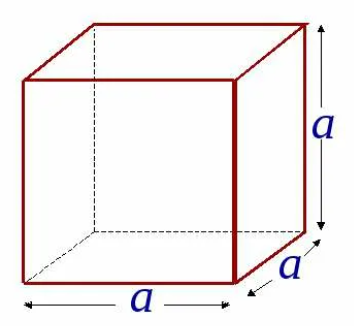
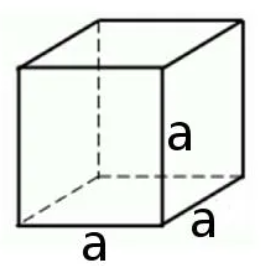
Куб

Прямоугольный параллелепипед, у которого все измерения равны, называется кубом. Поверхность куба состоит из шести равных квадратов (рисунок 4).

Для нахождения площади одной грани достаточно найти площадь квадрата по формуле S=a². Тогда для нахождения площади поверхности куба надо эту площадь умножить на 6, так как шесть равных граней у куба: S=6a²

Объем прямоугольного параллелепипеда

С понятием объема люди встречаются в повседневной жизни ежедневно. Мы наливаем воду в чайник, в ванну, другие жидкости в разные ёмкости – это всё измеряется в определенных единицах и является объемом. Наши шкафы, холодильники и другие подобные предметы – имеют объемы, так как мы их заполняем определенными вещами. На рисунке 5 показаны предметы, которые мы используем и которые имеют определенный объем.

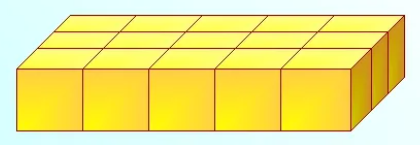
Рассмотрим объемные геометрические фигуры. Так, например, прямоугольный параллелепипед. Рассмотрим рисунок 6, где показано, что параллелепипед состоит из нескольких одинаковых кубиков. Значит, объем данного параллелепипеда равен сумме объемов его кубиков.

 

За единицу измерения объема выбирают куб, ребро которого равно единичному отрезку. Такой куб называют единичным.

Объем куба с ребром 1 мм называют кубическим миллиметром и записывают 1 мм³; с ребром 1 см – кубическим сантиметром (см³) и так далее. Измерить объем фигуры – значит подсчитать, сколько единичных кубов в ней помещается. Если объем маленького кубика на рисунке 3 принять за единицу, то объем нашего прямоугольного параллелепипеда будет равен 15 кубическим единицам.

Формула объема прямоугольного параллелепипеда

Чтобы найти объем прямоугольного параллелепипеда, надо перемножить три его измерения – длину, ширину и высоту. То есть V=abc (рисунок 4). Зная, что произведение длины и ширины – это есть площадь основания, получим, что V=(ab)h=Sh, где h – высота прямоугольного параллелепипеда. Таким образом, мы получили еще одну формулу для нахождения объема параллелепипеда.

Объем куба

Поскольку у куба все ребра равны (рисунок 7), то его объем вычисляется по формуле:

V=a³

Пирамида

Прямоугольный параллелепипед является одним из видов многогранников. Также одним из видов многогранника является пирамида, образ которой также известен нам из жизни – из истории и других источников (рисунок 9).

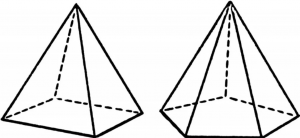
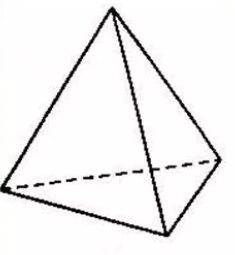
Поверхность пирамиды состоит из боковых граней – треугольников, которые имеют общую вершину, а в её основании могут быть различные многоугольники – треугольник, четырехугольник, пятиугольник и т.д. (рисунок 10).

Таким образом, пирамиды можно классифицировать по количеству сторон основания (треугольная, четырехугольная, пятиугольная и т.д.). Если пирамида треугольная (рисунок 11), то её основанием может служить любая грань.

Даниил Романович | Просмотров: 980

Математика

Тема 4: Площади и объемы

Урок 2: Прямоугольный параллелепипед

Вы открыли страницу вопроса Как найти длину и ширину прямоугольного параллелепипеда если известны объём и высота?. Он относится к категории
Математика. Уровень сложности вопроса – для учащихся 5 – 9 классов.
Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие
ответы по интересующей теме. Чтобы получить наиболее развернутый ответ,
можно просмотреть другие, похожие вопросы в категории Математика,
воспользовавшись поисковой системой, или ознакомиться с ответами других
пользователей. Для расширения границ поиска создайте новый вопрос, используя
ключевые слова. Введите его в строку, нажав кнопку вверху.