Как найти длину прямоугольного параллелепипеда дроби

Ответ или решение 2

1) Сначала запишем формулу нахождения объёма прямоугольного параллелепипеда:

V = a × b × h, где а — длина, b — ширина, h — высота.

2) Из формулы нахождения объёма парвллелепипеда выразим формулу нахождения длины:

Объём параллелепипеда 40 м.куб. Высота равна 4 м, ширина 2 м. Найдите длину параллелепипеда.

40 : 4 : 2 = 5 (м) — длина параллелепипеда.

Прямоугольный параллелепипед — пространственная фигура с шестью гранями, каждая из которых является прямоугольником. Противолежащие грани параллелепипеда равны.

По условию задан прямоугольный параллелепипед со следующими параметрами:

Объём прямоугольного параллелепипеда

Объём прямоугольного параллелепипеда V вычисляется как произведение площади основания многогранника и его высоты.

Площадь основания, которая представляет собой прямоугольник, выражается как произведение его длины и ширины, то есть

S (основания) = а * b.

Соответственно, V (прямоугольного параллелепипеда) = S (основания) * h = а * b * h.

Объём прямоугольного параллелепипеда равен произведению всех его параметров: высоты, ширины и длины.

Длина прямоугольного параллелепипеда

Таким образом, из приведенной выше зависимости можно выразить длину прямоугольного параллелепипеда:

Итак, длина прямоугольного параллелепипеда равна отношению его объема к произведению ширины и высоты.

Ответ

Проверено экспертом

Ответ:

Объем = длина * ширина * высота

длина = объем : (ширина * высота)

Пошаговое объяснение:

• Комментарии (2)
• Отметить нарушение

Ответ

Чтобы найти объем прямоугольного параллелепипеда, нужно умножить длину, ширину и высоту. Пример: Длина прямоугольного параллелепипеда равна 5 см, ширина — 10 см, а высота — 4 см, то объем такого прямоугольного параллелепипеда будет равен 4*5*10=200 см куб.

Объем прямоугольного параллелепипеда, формула.

Параллелепипедом является призма, основание у которой – это параллелограмм. У параллелепипеда

6 граней, а они, в свою очередь, являются параллелограммами.

Параллелепипед, у которого 4 боковые грани — это прямоугольники, является прямым

Прямой параллелепипед, у которого все 6 граней прямоугольники, является прямоугольным.

Другими словами, прямоугольный параллелепипед — это объемная фигура, у которой есть 6 граней, и

Объем прямоугольного параллелепипеда равен произведению площади основания на высоту:

где, H — высота параллелепипеда,

a – длина параллелепипеда,

b – ширина параллелепипеда,

h — высота прямоугольного параллелепипеда,

Примеры прямоугольного параллелепипеда: спортивный зал, кирпич, картонная коробка или столешница

Длины 3 рёбер прямоугольного параллелепипеда, которые имеют общий конец, называются измерениями

прямоугольного параллелепипеда.

Прямоугольный параллелепипед с одинаковыми измерениями является кубом. Все 6 граней куба — это

Квадрат длины диагонали прямоугольного параллелепипеда = сумме квадратов 3 его измерений.

Объем прямого параллелепипеда, формула.

Как найти объем параллелепипеда?

Площадь боковой поверхности параллелепипеда, формула:

где Р_о — периметр основания,

Площадь полной поверхности, формула

где S_о — площадь основания

Формула объёма прямого параллелепипеда:

Объем произвольного параллелепипеда.

Объём и соотношения в наклонном параллелепипеде часто определяются с помощью векторной алгебры.

Чему равен объём параллелепипеда? Объем параллелепипеда равен абсолютной величине смешанного

произведения трёх векторов, которые определяются 3-мя сторонами параллелепипеда, которые исходят

из одной вершины.

Соотношение длина сторон параллелепипеда – угол между ними даёт утверждение, что определитель

Грама указанных 3х векторов равен квадрату их смешанного произведения.

Представление о том, что такое прямоугольный параллелепипед, все имеют еще с детства, когда играли в кубики, держали в руках такие предметы, как коробка из-под сока или из- под конфет, видели аквариум такой формы. В жизни мы постоянно сталкиваемся с предметами, которые представляют собой прямоугольный параллелепипед (рисунок 1).

Определение

Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками. Грань – плоская поверхность предмета, составляющая угол с другой такой же поверхностью. Основания параллелепипеда – это его верхняя и нижняя грани.

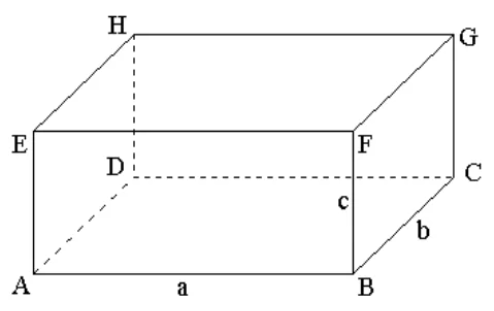
Так, на рисунке 2 показан прямоугольный параллелепипед ABCDEFGH. Он имеет 6 граней, основаниями являются грани ABCD и EFGH.

У параллелепипеда есть вершины, их 8. Они обозначены заглавными латинскими буквами. Также у прямоугольного параллелепипеда есть 12 ребер – это стороны граней: AB, BC, CD, AD, EF, FG, HG, EH, AE, BF, CG, HD.

Противоположные (не имеющие общих вершин) грани прямоугольного параллелепипеда равны.

Длина, ширина, высота

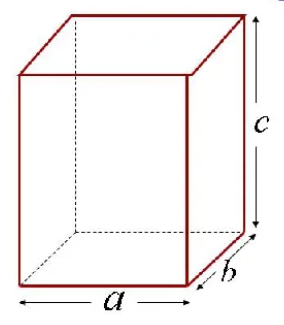
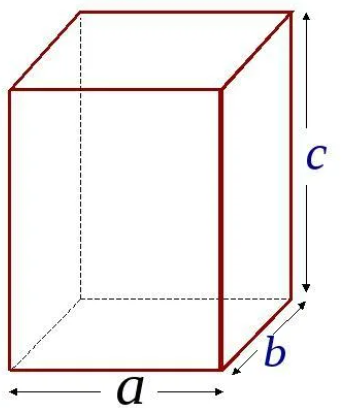
Прямоугольный параллелепипед имеет три измерения – длину (а), ширину (b) и высоту (c) – рисунок 3. Зная эти измерения, можно найти не только площадь каждой грани, но и площадь всей поверхности прямоугольного параллелепипеда.

Так как каждая грань параллелепипеда – это прямоугольник, то для нахождения площади любой грани надо умножить длину и ширину этих граней, т.е S=ab, S=bc, S=ac.

Для нахождения площади поверхности прямоугольного параллелепипеда надо сложить площади всех граней, то есть S поверхности = ab+bc+ac+ab+bc+ac. Так как противоположные грани равны, то их площади тоже равны, значит S поверхности = 2ab+2bc+2ac. Это действие можно записать короче, вынося 2 за скобки, как общий множитель, то есть S поверхности = 2(ab+bc+ac). Таким образом, нахождение площади поверхности становится более быстрым.

Куб

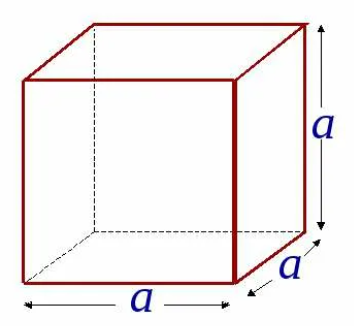
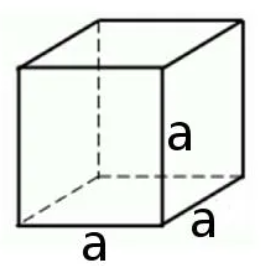
Прямоугольный параллелепипед, у которого все измерения равны, называется кубом. Поверхность куба состоит из шести равных квадратов (рисунок 4).

Для нахождения площади одной грани достаточно найти площадь квадрата по формуле S=a². Тогда для нахождения площади поверхности куба надо эту площадь умножить на 6, так как шесть равных граней у куба: S=6a²

Объем прямоугольного параллелепипеда

С понятием объема люди встречаются в повседневной жизни ежедневно. Мы наливаем воду в чайник, в ванну, другие жидкости в разные ёмкости – это всё измеряется в определенных единицах и является объемом. Наши шкафы, холодильники и другие подобные предметы – имеют объемы, так как мы их заполняем определенными вещами. На рисунке 5 показаны предметы, которые мы используем и которые имеют определенный объем.

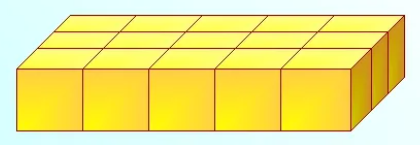
Рассмотрим объемные геометрические фигуры. Так, например, прямоугольный параллелепипед. Рассмотрим рисунок 6, где показано, что параллелепипед состоит из нескольких одинаковых кубиков. Значит, объем данного параллелепипеда равен сумме объемов его кубиков.

 

За единицу измерения объема выбирают куб, ребро которого равно единичному отрезку. Такой куб называют единичным.

Объем куба с ребром 1 мм называют кубическим миллиметром и записывают 1 мм³; с ребром 1 см – кубическим сантиметром (см³) и так далее. Измерить объем фигуры – значит подсчитать, сколько единичных кубов в ней помещается. Если объем маленького кубика на рисунке 3 принять за единицу, то объем нашего прямоугольного параллелепипеда будет равен 15 кубическим единицам.

Формула объема прямоугольного параллелепипеда

Чтобы найти объем прямоугольного параллелепипеда, надо перемножить три его измерения – длину, ширину и высоту. То есть V=abc (рисунок 4). Зная, что произведение длины и ширины – это есть площадь основания, получим, что V=(ab)h=Sh, где h – высота прямоугольного параллелепипеда. Таким образом, мы получили еще одну формулу для нахождения объема параллелепипеда.

Объем куба

Поскольку у куба все ребра равны (рисунок 7), то его объем вычисляется по формуле:

V=a³

Пирамида

Прямоугольный параллелепипед является одним из видов многогранников. Также одним из видов многогранника является пирамида, образ которой также известен нам из жизни – из истории и других источников (рисунок 9).

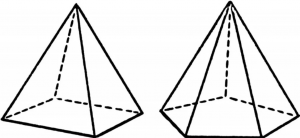
Поверхность пирамиды состоит из боковых граней – треугольников, которые имеют общую вершину, а в её основании могут быть различные многоугольники – треугольник, четырехугольник, пятиугольник и т.д. (рисунок 10).

Таким образом, пирамиды можно классифицировать по количеству сторон основания (треугольная, четырехугольная, пятиугольная и т.д.). Если пирамида треугольная (рисунок 11), то её основанием может служить любая грань.

Даниил Романович | Просмотров: 878

Математика

5 класс

Урок №82

Объём прямоугольного параллелепипеда

Перечень рассматриваемых вопросов:

– определение объёма прямоугольного параллелепипеда, если его стороны выражены обыкновенными дробями;

– выражение одних единиц измерения объёма через другие.

Тезаурус

Прямоугольный параллелепипед – это многогранник, со всех сторон ограниченный прямоугольниками, которые называются гранями.

Ребро – это отрезок, общий для двух граней параллелепипеда.

Вершина – это точка, в которой сходятся три ребра параллелепипеда.

Куб – это прямоугольный параллелепипед, у которого все ребра и грани равны.

Обязательная литература

1. Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС//С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.

Теоретический материал для самостоятельного изучения

Мы с вами уже знакомы с некоторыми пространственными телами: прямоугольный параллелепипед, куб, сфера, шар.

Вспомним, как выглядит прямоугольный параллелепипед, и назовём его элементы.

Снизу, сверху и с боков он ограничен прямоугольниками, которые называются гранями.

Нижняя и верхняя грань – это основания.

Грани пересекаются по отрезкам – рёбрам.

Точки, в которых пересекаются рёбра, называют вершинами.

Три ребра, которые сходятся в одной вершине, называют длиной, шириной и высотой.

Их ещё называют измерениями.

У прямоугольного параллелепипеда шесть граней, двенадцать рёбер и восемь вершин.

Куб – это прямоугольный параллелепипед, у которого все рёбра и грани равны.

Нам известно, что объём прямоугольного параллелепипеда вычисляется, как произведение a на b и на c. При этом мы считаем, что длина, ширина и высота выражены натуральными числами и измерены в одинаковых линейных единицах.

Эта формула будет верна и при дробных a, b и c.

V = a ∙ b ∙ с

Рассмотрим прямоугольный параллелепипед со сторонами

а = см, b = см и c = см.

Мы видим, что в этом случае объём равен:

(см³)

Достроим прямоугольный параллелепипед до куба со стороной 1 см. Площадь куба равна одному кубическому сантиметру.

V = 1 см³

Одно ребро куба разделено на 3 равные части, другое – на 2 и третье – на 5 равных частей.

Получили, что куб разделён на 30 одинаковых частей. Значит, объём каждой будет равен см³.

Прямоугольный параллелепипед состоит из четырёх таких частей, значит его объём будет равен:

(см³)

Итак, мы доказали, что если три ребра (а, b и c)прямоугольного параллелепипеда выражены одной линейной единицей и выражены обыкновенными дробями, то объём прямоугольного параллелепипеда равен произведению трёх его измерений.

Давайте теперь вспомним, как можно выразить одни единицы измерения объёма через другие.

1 см³ = 1000 мм³

1 дм³ = 1000 см³

1 м³ = 1000 дм³

1 км³ = 1 000 000 000 м³

Для измерения объёмов жидкостей и сыпучих веществ используют литры

1 л = 1 дм³

Меры объёма на Руси

На Руси использовали свои меры объёма

Ведро = бочки = 10 кружек = 100 чарок = 200 шкаликов = 12 литров

Кадь (кадка, какова) = 20 вёдер

В эпоху Киевской Руси везде употребляли кадь и ее доли.

В быту и торговле использовали различные хозяйственные сосуды: котлы, корчаги, ендовы, жбаны, братины.

При этом значение таких мер было различным в разных местах. Например, ёмкость котлов колебалась от полуведра до 20 вёдер.

В XVII в. была введена система кубических единиц, определяющая 7-футовую сажень, а также введён термин кубический (или «кубичный»).

Самые распространённые современные меры объёмов это:

1 литр = 1 дм³

1 миллилитр = 1 см³

Тренировочные задания

№ 1. Разместите нужные подписи под изображениями.

Правильный ответ: при выполнении данного задания нужно внимательно посмотреть на изображения. На верхнем рисунке мы видим многогранник, у которого все измерения равны. Значит, делаем вывод, что это куб. На нижнем изображении представлен многогранник, со всех сторон ограниченный прямоугольниками. Следовательно, это прямоугольный параллелепипед

№ 2. Вычислите объём куба, если его ребро равно м.

Чтобы решить это задание, необходимо вспомнить формулу для нахождения объёма куба: V = a³.

Правильный ответ: м³.

приведите дроби к наименьшему общему знаменателю 4/15, 7/20 и 3/10

×-1/2-45/6.
×5-5/64
674/67×

А+а-3,45+а+6,7=3а+6,7-3,45=3а+3,25

25 недель так как 176 делить на 7 25 с остатком но надо полных значит 25

Прямоугольный параллелепипед строится на ребрах трех длин, расположенных под прямым углом друг к другу. Зная ребра параллелепипеда, можно найти все возможные параметры, характеризующие его. В первую очередь, каждая грань параллелепипеда представляет собой прямоугольник с двумя одинаковыми сторонами, периметр же всего объемного тела ищется как умноженная на четыре сумма всех сторон-ребер параллелепипеда.
P=4(a+b+c)

Площадь прямоугольного параллелепипеда складывается из площадей всех его граней, то есть шести прямоугольников, попарно конгруэнтных. Площадь каждого прямоугольника равна произведению его сторон, поэтому чтобы найти площадь параллелепипеда, необходимо сложить эти произведения.
S=2ab+2bc+2ac=2(ab+bc+ac)

Чтобы вычислить объем прямоугольного параллелепипеда, зная его ребро, нужно перемножить их между собой, так как объем любого прямого тела с двумя основаниями равен произведению площади основания на высоту тела, а в основании параллелепипеда находится прямоугольник, площадь которого также равна произведению – его сторон.
V=abc

У прямоугольного параллелепипеда есть четыре диагонали – диагонали его боковых граней и основания, и диагональ самого параллелепипеда, проходящая через его внутреннее пространство. Все диагонали рассчитывается через прямоугольные треугольники по теореме Пифагора, где они являются гипотенузами. Для диагоналей боковых граней и основания катетами являются ребра параллелепипеда, а для четвертой диагонали, катеты представляют собой боковое ребро и диагональ основания. (рис. 22.1,22.2,22.3,22.4)
d_1=√(a^2+c^2 )
d_2=√(a^2+b^2 )
d_3=√(b^2+c^2 )
d_4=√(a^2+〖d_3〗^2 )=√(a^2+b^2+c^2 )

Угол α, образованный внутренней диагональю прямоугольного параллелепипеда и диагональю основания, можно вычислить через отношение тангенса – бокового ребра а и диагонали основания d3.(рис.22.5)
tan⁡α=a/d_3 =a/√(b^2+c^2 )