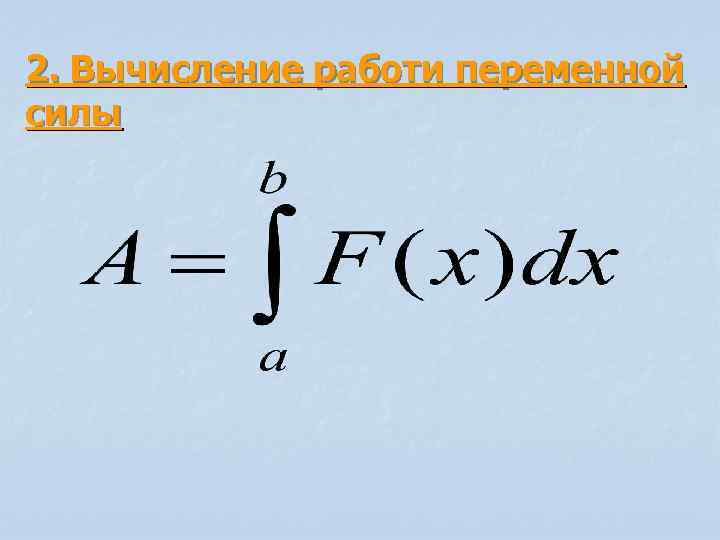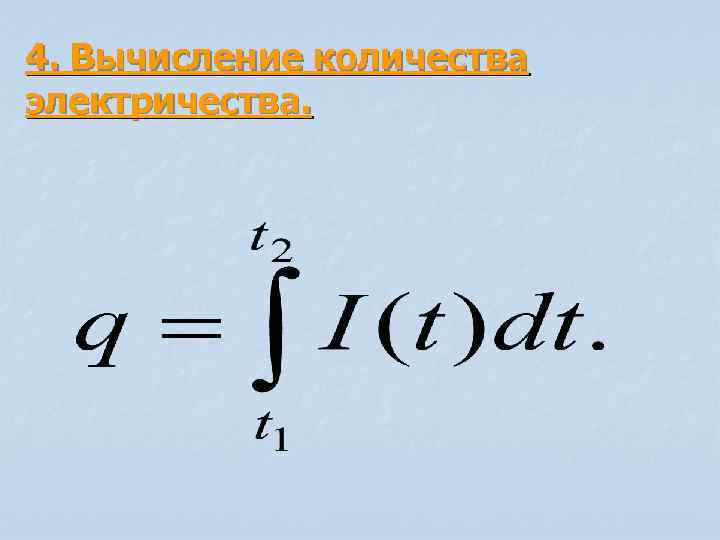Задача о вычислении длины пути по заданной скорости
Пусть точка
движется прямолинейно с переменной
скоростью
Вычислим длину пути, пройденного точкой
за промежуток времени от
до
Промежуток
разобьем произвольным образом на
элементарных промежутков
длины
В течение малого промежутка времени
скорость движения можно приближенно
считать постоянной и равной
где
некоторое
произвольное значение
из перомежутка
поэтому длина пути, пройденного за этот
промежуток приближенно равна
Складывая все частные длины
получаем приближенное значене длины
пути, пройденного точкой за промежуток
от
до
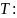
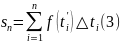
Переходя к пределу
при
находим точное значение длины пути
и в то же время получаем определенный
интеграл от функции
на отрезке
:
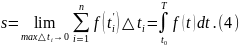
Таким образом,
физический смысл определенного интеграла
состоит в том, что если
скорость прямолинейного движения, то
определенный
интеграл (4) дает длину пути, пройденного
за промежуток времени от
до
Необходимое условие интегрируемости функции
Теорема. Если
функция
интегрируема на отрезке
то она и ограничена на этом отрезке.
Доказательство.
Необходимость этого условия покажем,
доказав утверждение: неограниченная
на отрезке
функция
не интегрируема на этом отрезке.
В самом деле, если
не ограничена на отрезке
то она не ограничена на некотором
элементарном отрезке
За счет выбора точки
интегральную сумму можно сделать сколь
угодно большой, а такая интегральная
сумма не имеет конечного предела.
Достаточно ли
ограниченности функции для существования
определенного интеграла ? Оказывается
, нет. Для того, чтобы доказать это,
достаточно найти хотя бы один пример,
показывающий, что интеграл для ограниченной
функции не существует.
Вот такой пример.
Функция Дирихле
На любом отрезке
эта функция ограничена, но не является
интегрируемой на нем. Действительно,
если в каждом элементарном отрезке
выбрать рациональную точку
то интегральная сумма
Если выбрать иррациональную точку
,
то
Предел интегральных сумм для функции
Дирихле не существует, поэтому функция
не является интегрируемой.
Отметим без
доказательства, что справедливы следующие
теоремы.
1. Если функция
интегрируема на отрезке
то она интегрируема на любом отрезке
содержащемся в
2. Если функция
непрерывна на отрезке
то она и интегрируема на этом отрезке.
3. Если функция
имеет на отрезке
конечное число точек разрыва первого
рода, то она интегрируема на
Свойства определенного интеграла
1.
Эта формула рассматривается как
соглашение. Она естественна с геометрической
точки зрения. Так как основание
криволинейной трапеции имеет длину,
равную нулю, то и площадь этой криволинейной
трапеции равна нулю.
2.
Эта формула также рассматривается как
соглашение. Она представляет собой
естественное обобщение понятия интеграла
на случай, когда отрезок
при
пробегается в направлении от
к
(в этом случае в интегральной сумме все
разности
имеют отрицательный знак).
3. Постоянный
множитель можно выносить за знак
определенного интеграла:
Доказательство.
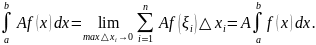
4. Определенный
интеграл от алгебраической суммы
нескольких функций равен алгебраической
сумме интегралов от слагаемых.
В случае двух
слагаемых:
Доказательство
аналогично предыдущему доказательству.
5. Если на отрезке
где
функции
и
удовлетворяют условию
то
Д
оказательство.
Рассмотрим разность:
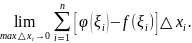
Здесь
Следовательно, каждое слагаемое суммы
неотрицательно, неотрицательна вся
сумма и неотрицателен ее предел, т.е.
откуда
Ч.т.д.
Если
и
то это свойство наглядно иллюстрируется
геометрически. Так как
то площадь криволинейной трапеции
не больше площади криволинейной трапеции
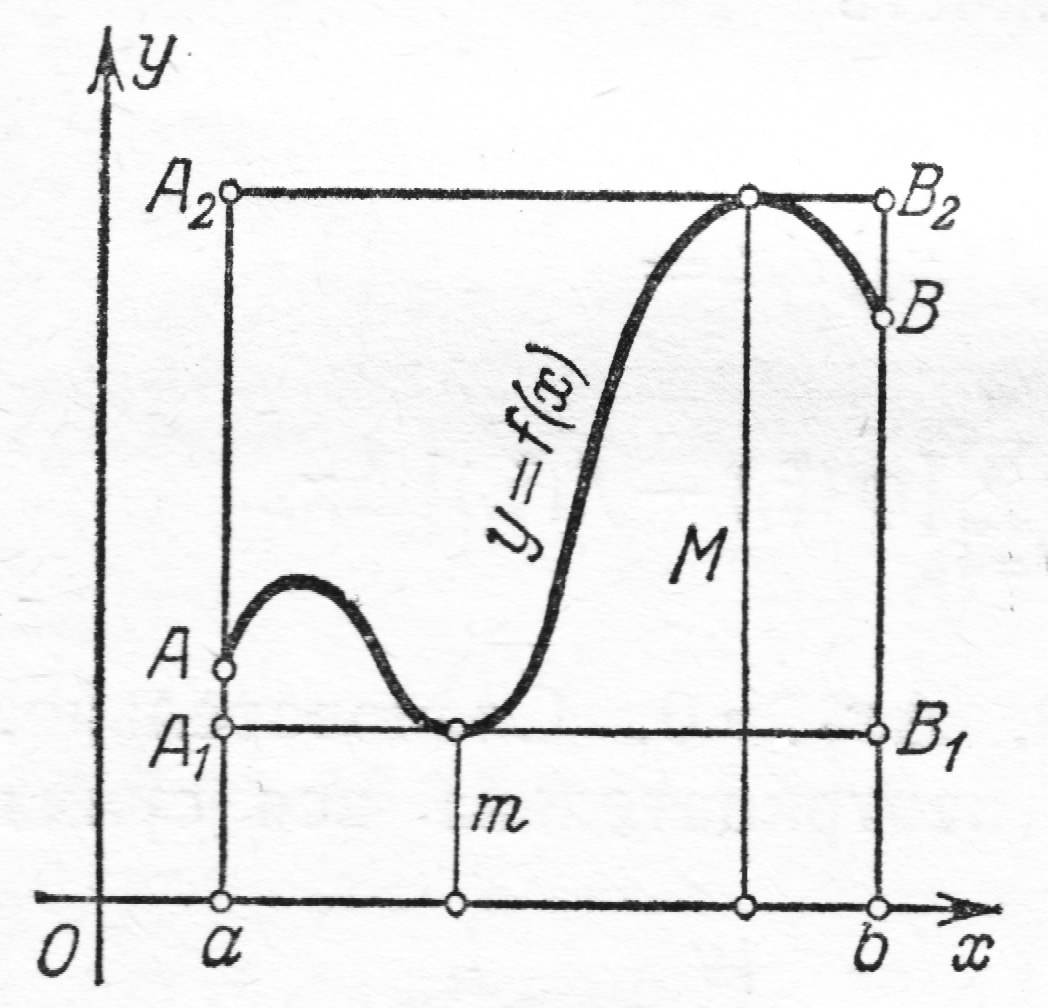
6. Оценка определенного
интеграла.
Если
и
наименьшее и наибольшее значения функции
на отрезке
и
то
Доказательство.
По условию
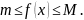
На основании
свойства 5 имеем:
Но
Подставляя, получим:
Если
то это свойство легко иллюстрируется
геометрически. Площадь криволинейной
трапеции
содержится между площадями прямоугольников
и
7
.
Теорема о среднем.
Если функция
непрерывна на отрезке
то на этом отрезке найдется такая точка
что справедливо следующее равенство:
Доказательство.
Пусть для определенности
В силу свойства 6:
Отсюда
где
Так как
непрарывна на
то она принимает все промежуточные
значения, заключенные между
и
Следовательно, при некотором значении
будет
т.е.
8. Для любых трех
чисел
справедливо равенство:
если только все
эти три интеграла существуют.
Доказательство.
Предположим сначала, что
и составим интегральную сумму для
функции
на отрезке
Так как предел интегральной суммы не
зависит от способа разбиения отрезка
на части, то мы будем разбивать отрезок
на малые отрезки так, чтобы точка
была точкой деления. Разобьем далее
интегральную сумму
соответствующую отрезку
на две суммы: сумму
соответствующую отрезку
и сумму
соответствующую отрезку
Тогда
Переходя к пределу
при
получим:
Если
то на основании доказанного можем
написать:
откуда с использованием
свойства 2 получаем:
А
налогичным
образом доказывается это свойство при
любом другом расположении точек
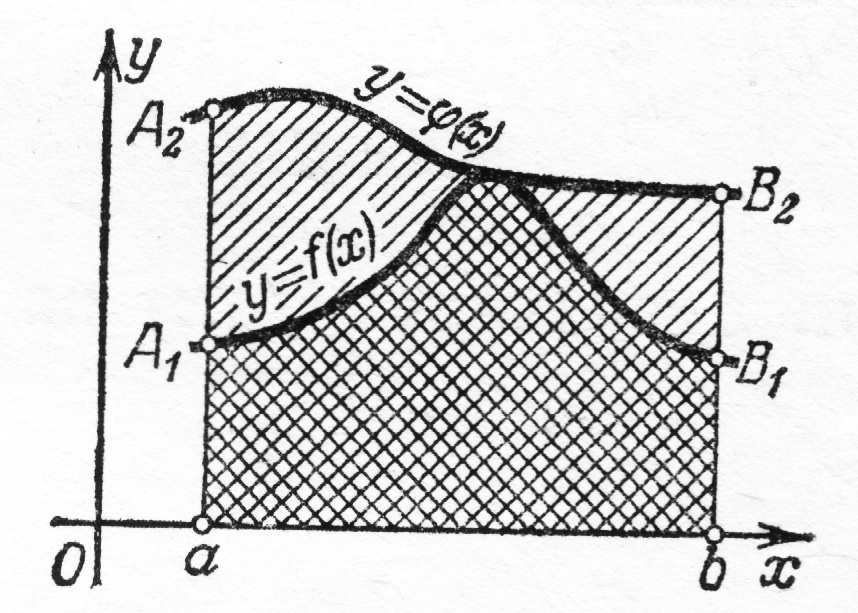
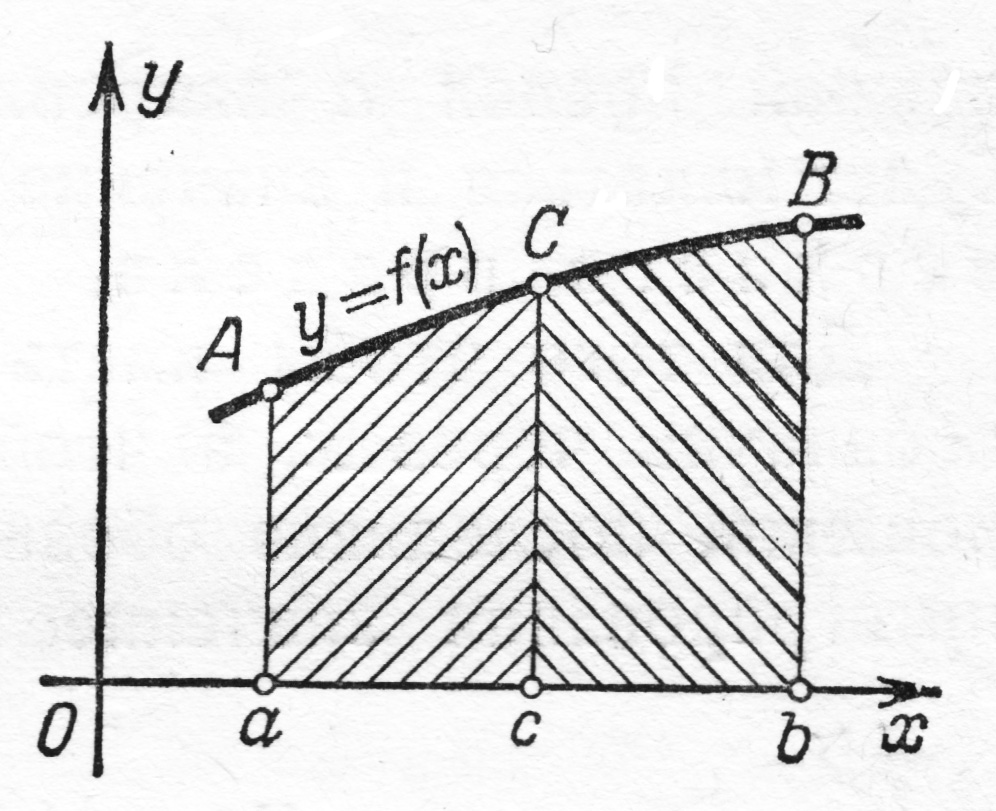
На рисунке дана
геометрическая иллюстрация свойства
8 для того случая, когда
и
площадь
трапеции
равна сумме площадей трапеций
и
Лекция 16.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Цель урока:
- обобщить и закрепить ключевые задачи по теме;
- научиться работать с теоретическими вопросами
темы; - научиться применять интеграл к решению
физических задач.
План урока:
1. Схема решения задач на приложения
определенного интеграла
2. Нахождение пути, пройденного телом при
прямолинейном движении
3. Вычисление работы силы, произведенной при
прямолинейном движении тела
4. Вычисление работы, затраченной на растяжение
или сжатие пружины
5. Определение силы давления жидкости на
вертикально расположенную пластинку
Тип урока: интегрированный.
Воспитательная работа: расширение
кругозора и познавательной деятельности
учащихся, развитие логического мышления и умения
применять свои знания.
Техническое обеспечение:
интерактивная доска. Компьютер и диск.
Приложение: «Рапсодия
природы».
ХОД УРОКА
I. Организационный момент
II. Постановка цели урока
– Урок хотелось бы провести под девизом
Готфрида Вильгельма Лейбница – немецкого философа,
логика,
математика,
физика:
«Общее искусство знаков представляет чудесное
пособие, так как оно разгружает воображение…
Следует заботиться о том, чтобы обозначения были
удобны для открытий. Обозначения коротко
выражают и отображают сущность вещей. Тогда
поразительным образом сокращается работа
мысли».
III. Повторим основные понятия и
ответим на вопросы:
– Скажите основное определение интеграла?
– Что вы знаете о интеграле (свойства, теоремы)?
– Знаете ли вы какие-нибудь примеры задач с
применением интеграла?
IV. Объяснение нового материала
(рассмотрение теории):
1. Схема решения задач на приложения
определенного интеграла
С помощью определенного интеграла можно решать
различные задачи физики, механики и т. д., которые
трудно или невозможно решить методами
элементарной математики.
Так, понятие определенного интеграла
применяется при решении задач на вычисление
работы переменной силы, давления жидкости на
вертикальную поверхность, пути, пройденного
телом, имеющим переменную скорость, и ряд других.
Несмотря на разнообразие этих задач, они
объединяются одной и той же схемой рассуждений
при их решении. Искомая величина (путь, работа,
давление и т. д.) соответствует некоторому
промежутку изменения переменной величины,
которая является переменной интегрирования. Эту
переменную величину обозначают через Х, а
промежуток ее изменения – через [а, b].
Отрезок [a, b] разбивают на n равных частей, в
каждой из которых можно пренебречь изменением
переменной величины. Этого можно добиться при
увеличении числа разбиений отрезка. На каждой
такой части задачу решают по формулам для
постоянных величин.
Далее составляют сумму (интегральную сумму),
выражающую приближенное значение искомой
величины. Переходя к пределу при , находят искомую величину
I в виде интеграла
I = , где f(x)
– данная по условиям задачи функция (сила,
скорость и т. д.).
2. Нахождение пути, пройденного телом при
прямолинейном движении
Как известно, путь, пройденный телом при
равномерном движении за время t, вычисляется по
формуле S = vt.
Если тело движется неравномерно в одном
направлении и скорость его меняется в
зависимости от времени t, т. е. v = f(t), то для
нахождения пути, пройденного телом за время от до
, разделим этот
промежуток времени на n равных частей Δt. В каждой
из таких частей скорость можно считать
постоянной и равной значению скорости в конце
этого промежутка. Тогда пройденный телом путь
будет приблизительно равен сумме , т.е.

Если функция v(t) непрерывна, то
Итак,
3. Вычисление работы силы, произведенной
при прямолинейном движении тела
Пусть тело под действием силы F движется по
прямой s, а направление силы совпадает с
направлением движения. Необходимо найти работу,
произведенную силой F при перемещении тела из
положения a в положение b.
Если сила F постоянна, то работа находится по
формуле
(произведение силы на длину пути).
Пусть на тело, движущееся по прямой Ох,
действует сила F, которая изменяется в
зависимости от пройденного пути, т. е. . Для того чтобы найти
работу, совершаемую силой F на отрезке пути от а
до b, разделим этот отрезок на n равных частей
. Предположим,
что на каждой части сила сохраняет постоянное значение
Составим интегральную сумму, которая
приближенно равна значению произведенной
работы:
т.е. работа, совершенная этой силой на участке
от а до b, приближенно мала сумме:
Итак, работа переменной силы вычисляется по
формуле: 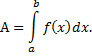
4. Вычисление работы, затраченной на
растяжение или сжатие пружины
Согласно закону Гука, сила F, необходимая для
растяжения или сжатия пружины, пропорциональна
величине растяжения или сжатия.
Пусть х – величина растяжения или сжатия
пружины. Тогда ,
где k – коэффициент пропорциональности,
зависящий от свойства пружины.
Работа на участке выразится формулой
, а вся затраченная работа
или
. Если
то погрешность величины
работы стремится к нулю.
Для нахождения истинной величины работы
следует перейти к пределу
Итак,
5. Определение силы давления жидкости на
вертикально расположенную пластинку
Из физики известно, что сила Р давления
жидкости на горизонтально расположенную
площадку S, глубина погружения которой равна h,
определяется по формуле:
, где
– плотность жидкости.
Выведем формулу для вычисления силы давления
жидкости на вертикально расположенную пластинку
произвольной формы, если ее верхний край
погружен на глубину a, а нижний – на глубину b.
Так как различные части вертикальной пластинки
находятся на разной глубине, то сила давления
жидкости на них неодинаковa. Для вывода формулы
нужно разделить пластинку на горизонтальных
полос одинаковой высоты . Каждую полосу приближенно
можно считать прямоугольником (рис.199).
По закону Паскаля сила давления жидкости на
такую полосу равна силе движения жидкости на
горизонтально расположенную пластинку той же
площади, погруженной на ту же глубину.
Тогда согласно формуле (4) сила давления на
полосу, находящуюся на расстоянии х от
поверхности, составит , где
– площадь полосы.
Составим интегральную сумму и найдем ее предел,
равный силе давления жидкости на всю пластинку:
т.е.
Если верхний край пластинки совпадает с
поверхностью жидкости, то а=0 и формула (5) примет
вид
Ширина каждой полосы зависит от формы
пластинки и является функцией глубины х
погружения данной полосы.
Для пластинки постоянной ширины формула (5)
упрощается, т.к. эту постоянную можно вынести за
знак интеграла:
V. Разбор задач по теме
1) Скорость движения материальной точки
задается формулой = (4
м/с.
Найти путь, пройденный точкой за первые 4с от
начала движения.
Решение:
2) Скорость движения изменяется по закону м/с . Найти длину
пути, пройденного телом за 3-ю секунду его
движения.
Решение:
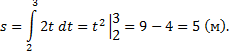
3) Скорость движения тела задана уравнением м/с. Определить
путь, пройденный телом от начала движения до
остановки.
Решение:
Скорость движение тела равна нулю в момент
начала его движения и остановки. Найдем момент
остановки тела, для чего приравняем скорость
нулю и решим уравнение относительно t; получим
Следовательно,
4) Тело брошено вертикально вверх со скоростью,
которая изменяется по закону м/с. Найти наибольшую высоту
подъема.
Решение:
Найдем время, в течении которого тело
поднималось вверх: 29,4–9,8t=0 (в момент наибольшего
подъема скорость равна нулю); t = 3 с. Поэтому
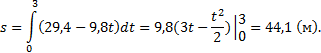
5) Какую работу совершает сила в 10Н при
растяжении пружины на 2 см?
Решение:
По закону Гука сила F, растягивающая пружину,
пропорциональна растяжению пружины , т.е. F = kx.
Используя условие, находим (Н/м), т.е. F = 500x. Получаем
6) Сила в 60Н растягивает пружину на 2 см.
Первоначальная длина пружины равна 14 см. Какую
работу нужно совершить, чтобы растянуть ее до 20
см?
Решение:
Имеем (H/м) и,
следовательно, F=3000x. Так как пружину требуется
растянуть на 0,06 (м), то
7) Определить силу давления воды на стенку
шлюза, длина которого 20 м, а высота 5 м (считая шлюз
доверху заполненным водой).
Здесь y = f(x) = 20, a = 0, b = 5 м, кг/
.
Находим
8) В воду опущена прямоугольная пластинка,
расположенная вертикально. Ее горизонтальная
сторона равна 1 м, вертикальная 2 м. Верхняя
сторона находится на глубине 0,5 м. Определить
силу давления воды на пластинку.
Решение:
Здесь y = 1, a = 0,5, b = 2 + 0,5 = 2,5 (м), = 1000 кг/
. Следовательно,
9) Скорость прямолинейного движения точки
задана уравнением . Найти уравнение движения точки.
Решение:
Известно, что скорость прямолинейного движения
тела равна производной пути s по времени t, т.е. , откуда ds = v dt.
Тогда имеем
Это искомое уравнение.
10) Скорость тела задана уравнением . Найти уравнение
движения, если за время тело прошло путь
.
Решение:
Имеем ds = v dt = (6+ 1) dt; тогда
Подставив в найденное уравнение начальные
условия s = 60 м, t = 3 c, получим
откуда С = 3.
Искомое уравнение примет вид
11) Тело движется со скоростью м/с. Найти закон движения s(t),
если в начальный момент тело находилось на
расстоянии 5 см от начала отсчета.
Решение:
Так как ds = v dt = (, то
Из условия следует, что если t = 0, то s = 5 см = 0,05 м.
подставив эти данные в полученное уравнение,
имеем откуда
0,05 = С.
Тогда искомое уравнение примет вид
12) Вычислить силу давления воды на плотину,
имеющую форму трапеции, у которой верхнее
основание, совпадающее с поверхностью воды,
имеет длину 10 м, нижнее основание 20 м, а высота 3 м.
Решение:
13) Цилиндрический стакан наполнен ртутью.
Вычислить силу давления ртути на боковую
поверхность стакана, если его высота 0,1 м, а
радиус основания 0,04 м. Плотность ртути равна 13600
кг/.
Решение:
Вычислим площадь круглой полоски
Элементарная сила давления составляет
Следовательно
VI. Самостоятельное решение задач на доске,
коллективный разбор решений задач:
- Скорость движения тела задана уравнением
. Найти уравнение
движения, если в начальный момент времени - Найти уравнение движения точки, если к моменту
начала отсчета она прошла путь, а его скорость задана
уравнением - Скорость движения тела пропорциональна
квадрату времени. Найти уравнение движения тела,
если известно, что за 3 с оно прошло 18 м. - Тело движется прямолинейно со скоростью
м/с. Найти путь,
пройденный телом за 5 с от начала движения. - Скорость движения тела изменяется по закону
м/с. Найти путь,
пройденный телом за 4 с от начала движения. - Найти путь пройденный телом за 10-ю секунду, зная,
что что скорость его прямолинейного движения
выражается формулойм/с.
- Найти путь, пройденный точкой от начала
движения до ее остановки, если скорость ее
прямолинейного движения изменяется по законум/с.
- Какую работу совершает сила в 8 Н при растяжении
пружины на 6 см? - Сила в 40 Н растягивает пружину на 0,04 м. Какую
работу надо совершить, чтобы растянуть пружину
на 0,02 м? - Вычислить силу давления воды на вертикальную
прямоугольную пластинку, основание которой 30 м, а
высота 10 м, причем верхний конец пластинки
совпадает с уровнем воды. - Вычислить силу давления воды на одну из стенок
аквариума, имеющего длину 30 см и высоту 20 см.
VII. Минутка релаксации
Запуск приложения «Минутка
релаксации»
VIII. Подведение итогов урока:
– Каким вопросам был посвящен урок?
– Чему научились на уроке?
– Какие теоретические факты обобщались на уроке?
– Какие рассмотренные задачи оказались наиболее
сложными? Почему?
Список литературы:
- Журнал «Потенциал»
- «Алгебра и начала анализа» 11 класс С.М.
Никольский, М.К. Потапов и др. - «Алгебра и математический анализ» Н.Я. Виленкин
и др. - «Учебник по математическому анализу» Град О.Г.,
Змеев О.А. - «Высшая математика: Учебник для вузов». В 3
томах. Бугров Я.С. Никольский С.М. - «Математический анализ». Е.Б. Боронина
При вычислении любой длины следует помнить, что это величина конечная, то есть просто число. Если имеется в виду длина дуги кривой, то такая задача решается с помощью определенного интеграла (в плоском случае) или криволинейного интеграла первого рода (по длине дуги). Дуга АВ будет обозначаться UАВ.
Первый случай (плоский). Пусть UАВ задана плоской кривой y = f(x). Аргумент функции изменятся в пределах от а до b и она непрерывно дифференцируема этом отрезке. Найдем длину L дуги UАВ (см. рис. 1а). Для решения этой задачи разбейте рассматриваемый отрезок на элементарные отрезки ∆xi, i=1,2,…,n. В результате UАВ разобьется на элементарные дуги ∆Ui, участков графика функции y=f(x) на каждом из элементарных отрезков. Найдете длину ∆Li элементарной дуги приближенно, заменив ее соответствующей хордой. При этом можно приращения заменить дифференциалами и использовать теорему Пифагора. После вынесения из квадратного корня дифференциала dx получите результат, приведенный на рисунке 1b.
Как вычислить длину кривой
Второй случай (дуга UАВ задана параметрически). x=x(t), y=y(t), tє[α,β]. Функции x(t) и y(t) имеют непрерывные производные на отрезке этом отрезке. Найдите их дифференциалы. dx=f’(t)dt, dy=f’(t)dt. Подставьте эти дифференциалы в формулу для вычисления длины дуги в первом случае. Вынесите dt из квадратного корня под интегралом, положите х(α)=а, x(β)=b и придете к формуле для вычисления длины дуги в данном случае (см. рис. 2а).
Третий случай. Дуга UАВ графика функции задана в полярных координатах ρ=ρ(φ) Полярный угол φ при прохождении дуги изменяется от α до β. Функция ρ(φ)) имеет непрерывную производную на отрезке ее рассмотрения. В такой ситуации проще всего использовать данные, полученные на предыдущем шаге. Выберите φ в качестве параметра и подставьте в уравнения связи полярных и декартовых координат x=ρcosφ y=ρsinφ. Продифференцируйте эти формулы и подставьте квадраты производных в выражение на рис. 2а. После небольших тождественных преобразований, основанных в основном, на применении тригонометрического тождества (cosφ)^2+(sinφ)^2=1, получите формулу для вычисления длины дуги в полярных координатах (см. рис.2b).
Четвертый случай (пространственная кривая, заданная параметрически). x=x(t), y=y(t), z=z(t) tє[α,β]. Строго говоря, здесь следует применить криволинейный интеграл первого рода (по длине дуги). Криволинейные интегралы вычисляют переводом их в обычные определенные. В результате ответ останется практическим таким же как и случае два, с тем лишь отличием, что под корнем появится добавочное слагаемое – квадрат производной z’(t) (см рис. 2с).
Примеры:
Пример 1. Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой у=ƒ(х), где а≤х≤ b.
Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю. Покажем, что если функция у=ƒ(х) и ее производная у’ = ƒ'(х) непрерывны на отрезке [а; b], то кривая АВ имеет длину, равную
Применим схему I (метод сумм).
1. Точками х0 = а, х1…, хn = b (х0 < x1 < …< хn) разобьем отрезок [а; b] на n частей (см. рис. 183). Пустьэтим точкам соответствуют точки М0 = А, M1,…,Mn =В на кривой АВ. Проведем хорды М0M1, M1M2,…, Мn-1Мn, длины которых обозначим соответственно через ΔL1, AL2,…, ΔLn. Получим ломаную M0M1M2 … Mn-ιMn, длина которой равна Ln=ΔL1 + ΔL2+…+ ΔLn =
2. Длину хорды (или звена ломаной) ΔL1 можно найти по теореме Пифагора из треугольника с катетами Δxi и Δуi:
По теореме Лагранжа о конечном приращении функции Δуi=ƒ'(сi)•Δхi, где ci є (xi-1;xi). Поэтому
а длина всей ломаной M0M1… Мn равна
3.Длина l кривой АВ, по определению, равна
.
Заметим, что при ΔLi→0 также и Δxi →0 ΔLi =и, следовательно, |Δxi|<ΔLi).
Функция непрерывна на отрезке [а; b], так как, по условию, непрерывна функция ƒ'(х). Следовательно, существует предел интегральной суммы (41.4), когда max Δxi→ 0:
Таким образом,или в сокращенной записи l =
Если уравнение кривой АВ задано в параметрической форме
где x(t) и y(t) — непрерывныефункции с непрерывными производными и х(а) = а, х(β) = b, то длина l кривой АВ находится по формуле
Формула (41.5) может быть получена из формулы (41.3) подстановкой x = x(t),dx = x'(t)dt,
Пример 2. Определить длину окружности x2 + y2 = r2. Решение. Вычислим сначала длину четвертой части окружности, лежащей в первом квадранте. Тогда уравнение дуги AB будет, откуда
,следовательно,
Длина всей окружности L = 2πr.
Пример 3. Найти длину дуги кривой y2 = x3 от x = 0 до x = 1 (y > 0). Решение. Дифференцируя уравнение кривой, найдем y’ = (3/2)x1/2, откуда
Пример 4. Пусть кривая лежит в плоскости x0y и описывается уравнением y = f(x).
Для нахождения длины дуги этой кривой, заключенной между точками с абсциссами a и b, разобьем дугу на столь малые элементы, чтобы каждый из них можно было аппроксимируовать прямолинейным участком (см. рисунок 1).
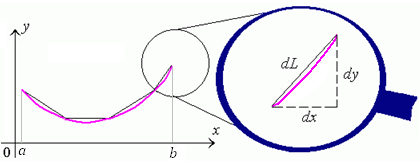
Рис. 1. Аппроксимация элемента дуги кривой прямолинейным участком.
Длину dL бесконечно малого участка можно выразить через dx и dy с помощью теоремы Пифагора:
 |
(1) |
где y ‘ – производная функции y = f(x) по переменной x.
Длина дуги равна сумме длин составляющих ее элементов:
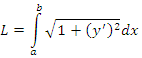 . . |
Пример 5.
Интегралы в физике
1. Вычисление пути по известным законам изменения скорости.
Решим задачу: Тело движется прямолинейно со скоростью, которая изменяется по закону v=2 t+1(м/с). Найти путь, который пройдёт тело за интервал времени от t 1 =1 c, до t 2 =3 c.
2. Вычисление работи переменной силы
Решим задачу: Вычислить работу, которую надо выполнить, чтобы откачать воду из ямы глубиной 4 м, имеющей квадратное сечение со стороною 2 м. Плотность воды ρ=103 кг/м 3.
3. Вычисление массы неоднородного стержня.
Решим задачу: Найти массу стержня длиной 35 см, если его линейная плотность изменяется по закону ρ(l)=(4 l+3)(кг/м)
4. Вычисление количества электричества.
Решим задачу: Найти количество электричества, проходящего через поперечное сечение проводника за 10 с, если сила тока изменяется по закону I(t)=(4 t+1)(A)
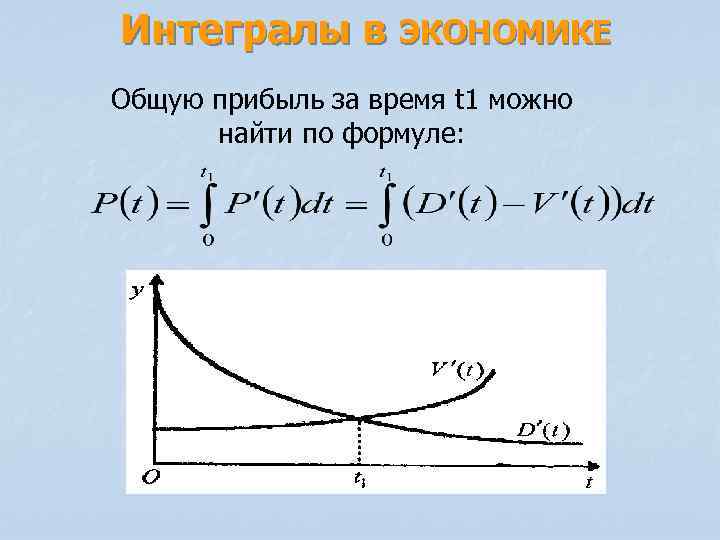
Интегралы в ЭКОНОМИКЕ Общую прибыль за время t 1 можно найти по формуле:
Интегралы в биологии Средняя длина пути, который пролетают птицы, пересекая некоторую фиксированную область, вычисляется по формуле:
Интегралы в быту Чтобы каша была вкусной, нужно такое отношение воды и круп:
Интегралы в науке Все процессы в природе, в которых постоянно меняются какие-то параметры, например время, температура, давление, координаты, изучаются и вычисляются только с помощью дифференциального и интегрального исчислений. Интегралы при этом только азы. Без них не вычислишь даже площадь какой-либо криволинейной поверхности. Математика вообще развивает логическое мышления, что всем полезно, Конечно, они забываются, если эти знания по жизни не востребованы. Но это не значит, что их вообще не нужно изучать. При обучении важно понять смысл мат аппарата в целом и научиться применять его к решению бытовых задач, выработать определенный стиль мышления при котором ты не будешь полагаться на интуицию принятии каких-то решений, а сможешь точно оценить результат и следствии поступков. Большинство интегралов получены как мат модели каких-либо естественных процессов в рамках медицины, биологии, химии, экономики, и т. д. Конкретно математический анализ, внутри которого выводятся методы решения интегралов, помогает понять откуда что взялось.
Интегралы в технике Также интегралы нашли себе широкое применение и в технике. Например в ПИД-регуляторе с использованием его интегральной составляющей. Её используют для устранения статической ошибки. Она позволяет регулятору учесть статическую ошибку.
Презентацию подготовил: Кирилл Ким
Синдбад Мореход
Мастер
(1554)
2 года назад
Для того, чтобы вычислить длину кривой, следует воспользоваться криволинейным интегралом первого рода. Он сводится к определенному интегралу по формулам, приведенным на картинке (строго говоря, перед корнем стоит множитель f(x,y), но для вычисления длин дуги принимается f(x,y)=1), в зависимости от описания кривой (декартовы координаты, полярные координаты или параметрическое задание).
Практические примеры советую посмотреть на mathprofi.ru
Мальвина в стрингах
Оракул
(65930)
2 года назад
Используя формулу, пределы функции, соответствующую систему координат.
Более подробно на картинке.
P.S. Для нахождения длины дуги необходимо уметь вычислять производную функции, поэтому рекомендую также почитать
об этом.
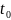
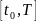
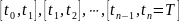
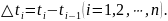
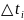
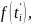
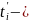

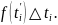
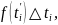
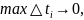
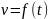
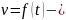

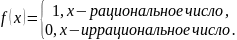
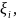

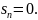
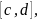

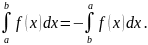
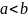
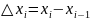
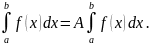
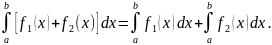
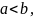

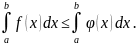
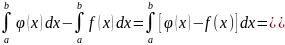
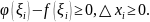


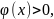
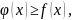
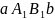

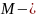
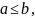
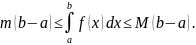
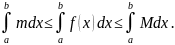
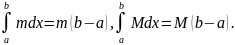


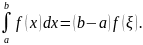
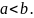


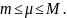

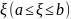
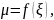
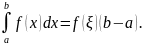
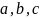

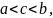
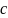
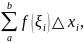
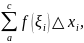
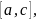
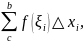
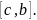
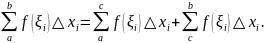
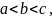
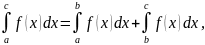

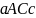
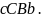
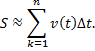
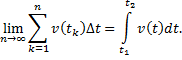
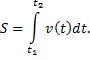
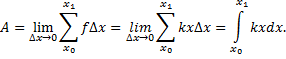
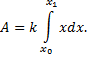
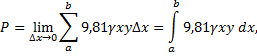
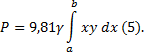
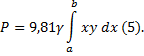
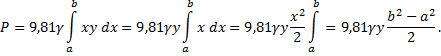
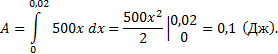
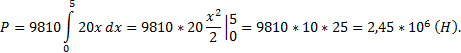
![1_5254fef39271a5254fef392758[1] 1_5254fef39271a5254fef392758[1]](https://ic.pics.livejournal.com/wrtorr/66163308/11897/11897_900.png)