Как найти длину пути дерева - Сайт, где вы сможете решить свои вопросы

Understanding the recursion

The path length can have simple recursive definition as follows.

The path length of a tree with N nodes is the sum of the path lengths of the subtrees of its root plus N-1.

First, you have to understand what the path length is: It is the sum of all the distances between the nodes and the root.

With this thought in mind, it is trivial to see that the path length for a root node without children is 0: There are no nodes with a distance to the root node.

Let’s assume we already know the path length of some trees. If we were to create a new node R, to which we connect all trees we already have, think about how the distances to the root node change.

Previously, the distances were measured to the root of the trees (now subtrees). Now, there’s one more step to be made to the root node, i.e. all distances increase by one.

Thus, we add N - 1, because there are N - 1 descendants from the root node, which are now all one further from the root , and 1*(N-1) = N-1

You calculate the path length easily in several ways, you can either count the edges or the nodes.

Counting Nodes

             A        Level 0
           /         
          B     C     Level 1
         /    / 
        D   E F   G   Level 2

We start with a path length of 0:

Node A is the root, which is always on level 0. It does not contribute to the path length. (You don’t need to follow any paths to reach it, hence 0)
- 0 + (0) = 0
On level 1, you have two nodes: B and C:
- 0 + (1 + 1) = 2
On level 2, you have four nodes: D, E, F and G:
- 2 + (2 + 2 + 2 + 2) = 10

Counting edges

             A        
           /         Level 1
          B     C     
         /    /     Level 2
        D   E F   G

0, our initial sum
+ 1*2 On level 1, there are 2 edges
+ 2*4 On level 2, there are 4 edges

Translating the definition into maths

A convinent way to compute the path length of a tree is to sum, for all k, the product of k and the umber of nodes at level k.

Let L_i denote the set of nodes on level i and h denote the height, i.e. maximum distance from a node to the root:

Источник

Тема: Деревья

Дерево
– это нелинейная
структура данных,
используемая при представлении
иерархических связей, имеющих отношения
«один ко многим».

Терминология
(взята из
ботаники и генеалогии)

Дерево
– это
совокупность
элементов, называемых узлами
или вершинами,
и отношений («родительских») между ними,
образующих иерархическую структуру
узлов.

Отношения
между узлами дерева (из генеалогии):

верхний
узел (вершина) называется родителем
(предком),

нижний
– потомком
(сыном или дочерней вершиной).

Определения
узлов – из ботаники.

Самая
верхняя вершина – корень,
а самые нижние вершины – листья.
Вершины,
не имеющие потомков, – терминальные
(через
отношения) или листья
(через определения).
Нетерминальные вершины – внутренние.

Корень
– родитель

ветви

братья
Узел – сын (потомок)

терминальная

вершина
(лист)
лист

Деревья
определяются рекурсивно,
т. е., дерево
с базовым типом Т
– это

либо
пустая структура (пустое дерево, один
корень);
либо
узел типа Т
с конечным числом древовидных структур
этого же типа Т,
называющихся поддеревьями.

Т.о.
– дерево без ветвей с одной вершиной –
это пустое
или нулевое
дерево.

Уровни:

Корень
дерева лежит на нулевом
уровне.

Максимальный
уровень какой-либо вершины дерева –
глубина
(от корня
до узла)
или высота
(от узла
до максимально удаленного листа).
Отсюда макс. уровень корня = 0.

Максимальный
уровень всех вершин называется
глубиной
дерева.

Число
непосредственных потомков у вершины
(узла) дерева называется
степенью
вершины (узла).

Максимальная
степень всех вершин является
степенью
дерева.

Число
ветвей от корня к вершине есть
длина пути
к этой
вершине.

Т.
о., корень имеет длину пути, равную 0,
длина пути его прямых (т. е., связанных
с ним одной ветвью) потомков равна 1 и
т.д. Вершина на уровне i
имеет длину пути i.

Длина
внутреннего пути дерева –
это сумма
длин путей для каждой его вершины.

Длина
внешнего пути дерева –
это сумма
длин путей всех специальных вершин,
которые дополняют дерево так, чтобы
степени всех вершин были равны степени
дерева:

длина
внешн. пути дерева = (Vi
* max степень
* hvi)
+ V1
*
степень,
где n
– количество вершин,Vi
– i-тая
вершина, hvi– глубина i-той
вершины.

Пример:

уровень
0

несуществующая

вершина

Глубина
дерева = 3.

Максимальная
степень дерева = 3.

Длина
внутреннего пути дерева равна 36.

Длина
внешнего пути дерева равна 120.

Представление
древовидной структуры

а)в виде
вложенных множеств:

D
F

E
G

B
C

б)
скобочное
(в выражениях)

(A(B(D(I),E(J,K,L)),
C(F(O),G(M,N),H(P))))

в) отступами (в
программах – структура)

А
	B
		D
			I
		E
			J
			K
			L
	C
		F
			O
		G
			M
			N
		H
			P

г)
в виде графа:

Представление
деревьев в памяти

В
памяти деревья можно представить в
виде:

а)
курсоров
на родителей;

б)
связного
списка сыновей;

в)
структуры
данных.

Пример:

Представление
этого дерева:

а)
в виде курсоров на родителей:

№ вершины
1 2 3 4 5 6 7 8 9 10

Т.
е., в этом представлении номер каждой
вершины дерева указывает на родителя.

б)
в виде связного списка сыновей:

в)
в виде структуры данных:

Nil
Nil

Возвращаясь
к терминологии:

Упорядоченное
дерево –
это такое дерево,
у которого все ветви, исходящие из одной
вершины, упорядочены.

Пример:

Деревья,
упорядоченные по алфавиту:

а)
в одном порядке б) в противоположном
порядке

Суть:
Деревья а и б – разные
упорядоченные деревья(!)

Позиционное
дерево –
это корневое дерево, у которого дети
любой вершины помечены номерами от 1 до
k.

К-ичное
дерево –
это дерево, у которого нет вершины более
чем с k
– детьми.

Полное
k-ичное
дерево –
это дерево, у которого все листья имеют
одинаковую глубину, а все внутренние
вершины – степень k.

Тем
самым, структура k-ичного
дерева полностью определена его высотой.
Т. о., количество листьев (n)
у k–ичного
дерева высотой k:

n
= k,
где h
– высота, равная соответственно h
= logkn.

Соседние файлы в папке ТСД. Лекции Силантьевой

Источник

Математические свойства бинарных деревьев

Прежде чем приступить к рассмотрению алгоритмов обработки деревьев, продолжим математическое исследование базовых свойств деревьев. Мы сосредоточим внимание на бинарных деревьях, поскольку они используются в книге чаще других. Понимание их основных свойств послужит фундаментом для понимания характеристик производительности различных алгоритмов, с которыми мы встретимся – не только тех, в которых бинарные деревья используются в качестве явных структур данных, но и рекурсивных алгоритмов “разделяй и властвуй “, и других аналогичных применений.

Лемма 5.5. Бинарное дерево с N внутренними узлами имеет N + 1 внешних узлов. Эта лемма доказывается методом индукции: бинарное дерево без внутренних узлов имеет один внешний узел, следовательно, для N = 0 лемма справедлива. Для N > 0 любое бинарное дерево с N внутренними узлами имеет к внутренних узлов в левом поддереве и N – 1 – к внутренних узлов в правом поддереве для некоторого к в диапазоне между 0 и N – 1, поскольку корень является внутренним узлом. В соответствии с индуктивным предположением левое поддерево имеет к + 1 внешних узлов, а правое поддерево – N – к внешних узлов, что в сумме составляет N + 1. ¦

Лемма 5.6. Бинарное дерево с N внутренними узлами имеет 2N ссылок: N – 1 ссылок на внутренние узлы и N + 1 ссылок на внешние узлы.

В любом дереве с корнем каждый узел, за исключением корня, имеет единственный родительский узел, и каждое ребро соединяет узел с его родительским узлом; следовательно, существует N – 1 ссылок, соединяющих внутренние узлы. Аналогично, каждый из N + 1 внешних узлов имеет одну ссылку на свой единственный родительский узел.

Характеристики производительности многих алгоритмов зависят не только от количества узлов в связанных с ними деревьях, но и от различных структурных свойств.

Определение 5.6. Уровень (level) узла в дереве – число, на единицу большее уровня его родительского узла (корень размещается на уровне 0). Высота (height) дерева – максимальный из уровней узлов дерева. Длина пути (path length) дерева – сумма уровней всех узлов дерева. Длина внутреннего пути (internal path length) бинарного дерева – сумма уровней всех внутренних узлов дерева. Длина внешнего пути (external path length) бинарного дерева – сумма уровней всех внешних узлов дерева.

Удобный способ вычисления длины пути дерева заключается в суммировании произведений k на число узлов на уровне к для всех натуральных чисел k.

Для этих величин существуют также простые рекурсивные определения, вытекающие непосредственно из рекурсивных определений деревьев и бинарных деревьев. Например, высота дерева на 1 больше максимальной высоты поддеревьев его корня, а длина пути дерева с N узлами равна сумме длин путей поддеревьев его корня плюс N – 1. Приведенные величины также непосредственно связаны с анализом рекурсивных алгоритмов. Например, для многих рекурсивных вычислений высота соответствующего дерева в точности равна максимальной глубине рекурсии, то есть размеру стека, необходимого для поддержки вычисления.

Лемма 5.7. Длина внешнего пути любого бинарного дерева, имеющего N внутренних узлов, на 2N больше длины внутреннего пути.

Эту лемму можно было бы доказать методом индукции, но существует другое, более наглядное, доказательство (которое применимо и для доказательства леммы 5.6). Обратите внимание, что любое бинарное дерево может быть создано при помощи следующего процесса. Начинаем с бинарного дерева, состоящего из одного внешнего узла. Затем повторяем N раз следующее: выбираем внешний узел и заменяем его новым внутренним узлом с двумя дочерними внешними узлами. Если выбранный внешний узел находится на уровне к, длина внутреннего пути увеличивается на к, но длина внешнего пути увеличивается на к + 2 (удаляется один внешний узел на уровне к, но добавляются два на уровне к + 1). Этот процесс начинается с дерева, длина внутреннего и внешнего путей которого равны 0, и на каждом из N шагов длина внешнего пути увеличивается на 2 больше, чем длина внутреннего пути.

Лемма 5.8. Высота бинарного дерева с N внутренними узлами не меньше lgN и не больше N – 1.

Худший случай – вырожденное дерево, имеющее только один лист и N – 1 ссылок от корня до этого листа (см.
рис.
5.23). В лучшем случае мы имеем уравновешенное дерево с 2ⁱ внутренними узлами на каждом уровне i, за исключением самого нижнего (см.
рис.
5.23). Если его высота равна h, то должно быть справедливо соотношение

$2^{h -1}<N+1leq2^{h}$

поскольку существует N + 1 внешних узлов. Из этого неравенства и следует данная лемма: в лучшем случае высота равна lgN, округленному до ближайшего целого числа.

Лемма 5.9. Длина внутреннего пути бинарного дерева с N внутренними узлами не меньше чем N lg(N/ 4) и не превышает N(N – 1)/ 2.

Худший и лучший случай соответствуют тем же деревьям, которые упоминались при доказательстве леммы 5.8 и показаны на
рис.
5.23. В худшем случае длина внутреннего пути дерева равна 0 + 1 + 2 + … + (N – 1) = N(N – 1)/2. В лучшем случае дерево имеет N + 1 внешних узлов при высоте, не превышающей . Перемножив эти значения и применив лемму 5.7, получим предельное значение .

Как мы увидим, бинарные деревья часто используются в компьютерных приложениях, и максимальная производительность достигается тогда, когда бинарные деревья полностью (или почти) сбалансированы. Например, деревья, которые использовались для описания алгоритмов “разделяй и властвуй “, подобных бинарному поиску и сортировке слиянием, полностью сбалансированы (см. упражнение 5.74).

В
“Очереди с приоритетами и пирамидальная сортировка”
и
“Сбалансированные деревья”
будут рассмотрены структуры данных, основанные на уравновешенных деревьях.

Эти основные свойства деревьев предоставляют информацию, необходимую для разработки эффективных алгоритмов решения многих практических задач. Более подробный анализ нескольких особых алгоритмов, с которыми придется встретиться, требует сложных математических выкладок, хотя часто полезные приближенные оценки можно получить с помощью простых индуктивных рассуждений, подобных использованным в этом разделе. В последующих главах мы продолжим рассмотрение математических свойств деревьев по мере возникновения необходимости. А пока можно вернуться к теме алгоритмов.

Рис.
5.23.
Три бинарных дерева с 10 внутренними узлами

Бинарное дерево, показанное вверху, имеет высоту 7, длину внутреннего пути 31 и длину внешнего пути 51. Полностью сбалансированное бинарное дерево (в центре) с 10 внутренними узлами имеет высоту 4, длину внутреннего пути 19 и длину внешнего пути 39 (ни одно двоичное дерево с 10узлами не может иметь меньшее значение любого из этих параметров). Вырожденное дерево (внизу) с 10 внутренними узлами имеет высоту 10, длину внутреннего пути 45 и длину внешнего пути 65 (ни одно бинарное дерево с 10 узлами не может иметь большее значение любого из этих параметров).

Упражнения

5.68. Сколько внешних узлов существует в M -арном дереве с N внутренними узлами? Используйте свой ответ для определения объема памяти, необходимого для представления такого дерева, если считать, что каждая ссылка и каждый элемент занимает одно слово памяти.

5.69. Приведите верхнее и нижнее граничные значения высоты M -арного дерева с N внутренними узлами.

5.70. Приведите верхнее и нижнее граничные значения длины внутреннего пути M -арного дерева с N внутренними узлами.

5.71. Приведите верхнее и нижнее граничные значения количества листьев в бинарном дереве с N узлами.

5.72. Покажите, что если уровни внешних узлов в бинарном дереве различаются на константу, то высота дерева составляет O(logN).

5.73. Дерево Фибоначчи высотой n > 2 – это бинарное дерево с деревом Фибоначчи высотой n – 1 в одном поддереве и дерево Фибоначчи высотой n – 2 – в другом. Дерево Фибоначчи высотой 0 – это единственный внешний узел, а дерево Фибоначчи высотой 1 – единственный внутренний узел с двумя внешними дочерними узлами (см.
рис.
5.14). Выразите высоту и длину внешнего пути для дерева Фибоначчи высотой n в виде функции от N (количество узлов в дереве).

5.74. Дерево вида “разделяй и властвуй “, состоящее из N узлов – это бинарное дерево с корнем, обозначенным N, деревом “разделяй и властвуй ” из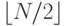 узлов в одном поддереве и деревом “разделяй и властвуй ” из узлов в другом. (Дерево “разделяй и властвуй ” показано на
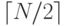
рис.
5.6.) Нарисуйте дерево “разделяй и властвуй ” с 11, 15, 16 и 23 узлами.

5.75. Докажите методом индукции, что длина внутреннего пути дерева вида “разделяй и властвуй ” находится в пределах между N lgN и N lgN + N.

5.76. Дерево вида “объединяй и властвуй “, состоящее из N узлов – это бинарное дерево с корнем, обозначенным N, деревом “объединяй и властвуй ” из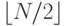 узлов в одном поддереве и деревом “объединяй и властвуй ” из узлов в другом (см. упражнение 5.18). Нарисуйте дерево “объединяй и властвуй ” с 11, 15, 16 и 23 узлами.

5.77. Докажите методом индукции, что длина внутреннего пути дерева вида “объединяй и властвуй ” находится в пределах между N lgN и N lgN + N.

5.78. Полное (complete) бинарное дерево – это дерево, в котором заполнены все уровни, кроме, возможно, последнего, который заполняется слева направо, как показано на
рис.
5.24. Докажите, что длина внутреннего пути полного дерева с N узлами лежит в пределах между N lgN и N lgN + N.

Рис.
5.24.
Полные бинарные деревья с семью и десятью внутренними узлами

Если количество внешних узлов является степенью 2 (верхний рисунок), то все внешние узлы в полном бинарном дереве находятся на одном уровне. В противном случае (нижний рисунок) внешние узлы располагаются на двух уровнях, причем внутренние узлы находятся слева от внешних узлов предпоследнего уровня.

Источник

Двоичное дерево

Предварительный обход (рекурсивные и рекурсивные алгоритмы)

Последующий обход (рекурсия и рекурсивный алгоритм)

Обход по порядку (рекурсивные и рекурсивные алгоритмы)

Обход последовательности

Углубленное исследование кодирования Хаффмана

В двух вышеупомянутых разделах мы обсудили два метода реализации обобщенных деревьев, а также метод «таблица дочерних узлов» и метод «крайний левый дочерний узел / правый родственный узел». Дерево, реализованное этими двумя методами, представляет собой многодерево, которое подходит для описания любой древовидной структуры. В этом разделе мы обсудим особое дерево – двоичное дерево. По сравнению с обобщенными деревьями, двоичные деревья имеют определенную структуру, включая взаимосвязь между количеством внутренних и внешних узлов, взаимосвязь между количеством узлов и высотой дерева и т. Д. В этом разделе будут рассмотрены различные алгоритмы обхода бинарных деревьев, включая алгоритмы обхода предварительного, среднего, последующего и уровня слоев. Наконец, в этой главе будет изучено специальное двоичное дерево, широко используемое в информационных технологиях, а именно дерево Хаффмана.

Математические свойства бинарных деревьев

Прежде чем обсуждать различные алгоритмы бинарных деревьев, давайте подробно обсудим математические свойства бинарных деревьев.

Свойство X.1. Бинарное дерево с N внутренними узлами имеет N + 1 внешний узел.

Доказательство. Доказательство по индукции.

Когда N = 0, двоичное дерево с 0 внутренними узлами имеет 1 внешний узел, поэтому свойство сохраняется, когда N = 0.

Когда N> 0, предположим, что любое двоичное дерево с M (M <N) внутренними узлами имеет M + 1 внешних узлов. Любое двоичное дерево с N внутренними узлами имеет k внутренних узлов в левом поддереве, N-1-k внутренних узлов в правом поддереве и сам корневой узел, где k находится между 0 и N-1. Согласно предположению индукции, левое поддерево имеет k + 1 внешних узлов, а правое поддерево имеет N-k внешних узлов, всего N + 1 внешних узлов.

■

Свойство X.2. Двоичное дерево с N внутренними узлами имеет 2N ссылок: N-1 ссылки на внутренние узлы и N + 1 ссылки на внешние узлы.

Доказательство: В корневом дереве любой узел, кроме корневого, имеет родительский узел, а также связан с краем своего родительского узла, поэтому с внутренними узлами связано N-1 ссылок. Согласно свойству 1, в дереве N + 1 внешних узлов, каждый внешний узел имеет родительский узел, и все N + 1 ссылки подключены к внешним узлам.

■

Определение Количество узлов в дереве на один уровень выше, чем количество родительских узлов, а корневой узел находится на уровне 0. Высота дерева – это максимальное значение среди уровней узлов в дереве. Длина пути дерева – это сумма уровней всех узлов дерева. Длина внутреннего пути двоичного дерева – это сумма количества слоев всех внутренних узлов дерева. Длина внешнего пути двоичного дерева – это сумма количества слоев всех внешних узлов дерева.

Свойство X.3. Длина внешнего пути любого двоичного дерева с N внутренними узлами на 2N больше, чем длина внутреннего пути.

Доказательство: процесс создания двоичного дерева: начиная с двоичного дерева, содержащего внешний узел, повторите следующие шаги N раз:

Выберите внешний узел и замените внешний узел новым внутренним узлом с двумя внешними узлами в качестве дочерних узлов.

Если количество слоев выбранного внешнего узла равно k, поскольку добавляется внутренний узел с номером слоя k, длина внутреннего пути увеличивается на k; в то же время внешний узел с номером слоя k является удаляются и добавляются два слоя. Это внешний узел k + 1, что приводит к увеличению пути внешнего узла на k + 2.

Весь процесс создания двоичного дерева начинается с того, что внутренний путь и внешний путь равны 0. Для каждого из N шагов длина внешнего пути увеличивается на 2 больше, чем длина внутреннего пути, поэтому общая сумма равна 2N.

■

Свойство X.4. Высота двоичного дерева с N внутренними узлами не меньше lgN и не больше N-1.

Доказательство: наивысший случай – вырожденное дерево только с одним листовым узлом, N-1 связывает корневой узел с листовым узлом, а самый короткий случай – это то, что на каждом слое с i, кроме нижнего, есть 2i. Внутренние узлы, если высота равна h, потому что имеется N + 1 внешних узлов, то соотношение будет следующим:

2h-1 < N + 1 ≤ 2h

Таким образом, минимальная высота – это целое число lgN, полученное округлением в большую сторону.

■

Свойство X.5 Длина внутреннего пути двоичного дерева с N внутренними узлами составляет не менее Nlg (N / 4) и не более N (N-1) / 2.

Доказательство: Максимальный и минимальный внутренние пути такие же, как те, что обсуждаются в свойстве 4. В максимальном случае длина внутреннего пути дерева равна 0 + 1 + 2 + … + (n-1) = N (N -1) / 2.

В самом маленьком случае имеется N + 1 внешних узлов, а высота дерева не превышает [lgN], предел длины внешнего пути составляет (N + 1) [lgN], согласно свойству 3, длина внутреннего пути предел равен (N + 1) [lgN] -2N <Nlg (N / 4).

■

Двоичные деревья широко используются в компьютерных технологиях, и их производительность лучше всего, когда они полностью сбалансированы или близки к равновесию. Мы обнаружим производительность сбалансированного дерева, когда объясним алгоритм поиска в серии.

Основные свойства деревьев предоставляют нам информацию для разработки некоторых университетских алгоритмов для решения практических задач. Для более подробного анализа конкретных алгоритмов, с которыми мы столкнемся, необходимы очень сложные математические инструменты. Заинтересованные читатели могут обратиться к соответствующим книгам. Далее мы сосредоточимся на алгоритмах, связанных с бинарными деревьями.

Обход двоичного дерева

В этом разделе мы в основном рассмотрим алгоритм обхода дерева, то есть, учитывая дерево, цель может систематически посещать каждый узел. При доступе к каждому узлу в структуре данных, такой как связанный список, мы можем посещать каждый узел за раз в соответствии с конкретной структурой связанного списка. Однако в структуре двоичного дерева, поскольку каждый узел может иметь отношение соединения с двумя узлов, нам может понадобиться определить правила доступа.

В предыдущих разделах, когда мы обсуждали обобщенный алгоритм обхода дерева, мы уже задействовали обобщенные алгоритмы обхода до и после порядка дерева. Мы также пришли к выводу, что алгоритм обхода до порядка в обобщенном дереве больше соответствует нашим фактическим знаниям. Здесь мы подробно обсудим алгоритмы обхода предварительного, среднего, пост-порядка и порядка слоев двоичного дерева.

Preoeder Мы посещаем узел, а затем посещаем левое и правое поддеревья узла;

Inorder (inorder) Мы посещаем левое поддерево точки, затем узел и, наконец, правое поддерево узла;

Поступорядочение (postorder) Мы посещаем левое и правое поддеревья узла, а затем посещаем узел;

Levelorder Мы посещаем каждый узел слева направо слой за слоем.

Мы можем легко реализовать эти алгоритмы с помощью рекурсивных программ, здесь мы будем реализовывать различные алгоритмы обхода с рекурсивными и нерекурсивными методами.

Структура данных узла двоичного дерева

Прежде чем подробно обсуждать алгоритм обхода дерева, мы сначала обсудим конструкцию узла двоичного дерева. Каждый узел двоичного дерева содержит содержимое узла, то есть элемент элемента, в дополнение к указателям слева и справа. дочерние узлы.

Следует отметить, что позже мы представим специальное двоичное дерево, а именно двоичное дерево поиска. Его структурная особенность состоит в том, что элемент элемента узла больше элемента элемента любого узла в левом поддереве и меньше любого элемента. узел в правом поддереве Элементы элемента. Но между элементами двоичного дерева, которое мы будем здесь обсуждать, нет такой структуры, поэтому, когда мы создаем двоичное дерево здесь, мы используем тот же метод искусственного сложения, который мы обсуждали обобщенное дерево в предыдущих двух разделах.

Структура данных узла двоичного дерева реализована следующим образом:

package Tree;

import Element.ElemItem;

    /**
     *
Двоичное дерево, цель этой структуры – различные алгоритмы обхода двоичного дерева и т. д.
     */

    public class LinkBinTreeNode implements Comparable{

        //Переменная частного члена
        private ElemItem elem;

        //Левый и правый дочерние узлы
        private LinkBinTreeNode leftNode;

        private LinkBinTreeNode rightNode;

        //Конструктор без параметров
        public LinkBinTreeNode(){

            elem = null;

            leftNode = null;

            rightNode = null;

        }

        //Конструктор с параметрами
        public LinkBinTreeNode(ElemItem _e,

                    LinkBinTreeNode _l,

                    LinkBinTreeNode _r){

            elem = _e;

            leftNode = _l;

            rightNode = _r;

        }

        //Получить элемент
        public ElemItem getElem(){

            return elem;

        }

        //Установить элемент элемента
        public void setElem(ElemItem _elem){

            elem = _elem;

        }

        //Получите левый дочерний узел
        public LinkBinTreeNode getLeft(){

            return leftNode;

        }

        //Сбросить левый дочерний узел
        public void setLeft(LinkBinTreeNode lft){

            leftNode = lft;

        }

        //Получите правильный дочерний узел
        public LinkBinTreeNode getRight(){

            return rightNode;

        }

        //Сбросить правый дочерний узел
        public void setRight(LinkBinTreeNode rgt){

            rightNode = rgt;

        }

        //Определите, является ли узел листовым.
        public boolean isLeaf(){

            return (leftNode == null) &&

                    (rightNode == null);

        }

        //Строка возврата
        public String toString(){

            return elem.getElem().toString();

        }

        //Реализуйте интерфейсные функции
        public int compareTo(Object arg0) {

            return elem.compareTo((ElemItem)arg0);

        }

    }

Обход предзаказа

Алгоритм обхода предварительного порядка сначала посещает сам узел, а затем один раз посещает левое поддерево и правое поддерево узла. Чтобы определить этот процесс с рекурсивной точки зрения, его можно определить следующим образом: если узел не является пустым узлом, сначала посетите сам узел, а затем рекурсивно посетите левое и правое поддеревья узла. В предыдущей главе, когда мы обсуждали структуру стека, мы обсуждали эквивалентный рекурсивный процесс реализации рекурсивного алгоритма, то есть вы можете сохранить параметры текущей программы через стек, перейти к другой программе, а затем выскочить параметры стека после завершения и продолжить выполнение программы. Далее мы сначала обсудим этот процесс на примере преамбулы двоичного дерева.

На рисунке показано двоичное дерево. Предварительный заказ просматривает каждый узел в дереве и посещает элементы каждого узла. Результатом будет:

1→2→4→6→10→-1→7→5→8→9→3→14→11→12→13

При использовании рекурсивного алгоритма для достижения обхода перед порядком сначала используйте указатель узла rt, чтобы указать на корневой узел двоичного дерева, а затем рекурсивно обойти все узлы в двоичном дереве следующим образом:

    rec_preorder(rt){

        1.    if(rt == null) return;

            //Сначала посетите родительский узел
        2.    Visit(rt);

            //Затем посетите левый дочерний узел
        3.    rec_preorder(rt.getLeft());

            //Последнее посещение правого дочернего узла
        4.    rec_preorder(rt.getRight());

    }

Во время выполнения сначала посетите узел n14, а затем рекурсивно пройдитесь по левому поддереву n14, то есть поддереву с n8 в качестве корневого узла; сначала посетите узел n8, а затем рекурсивно пройдитесь по поддереву с n4 в качестве корневого узла; посетите узел сначала n4, затем рекурсивно пройти поддерево с n2 в качестве корневого узла; сначала посетить узел n2, а затем рекурсивно пройти поддерево с n1 в качестве корневого узла; сначала посетить узел n1, так как левое поддерево n1 пусто, затем посетить n1 Правое поддерево узла n2, поддерево является деревом с одним узлом, поэтому после прямого доступа к узлу n0 обход поддерева с n1 в качестве корневого узла заканчивается; в это время при обратном отслеживании к правому поддереву узла n2, поддерево пусто, поэтому обход поддерева с n2 в качестве корневого узла заканчивается; программа возвращается к поддереву с n4 в качестве корневого узла и рекурсивно проходит поддерево с n3 в качестве корневого узла. Это поддерево является одноузловым. дерево, поэтому после прямого посещения узла n3 оно заканчивается на n4 – это обход поддерева корневого узла; программа возвращается к поддереву с n8 в качестве корневого узла и рекурсивно проходит по поддереву с n7 в качестве корневого узла. В том же анализе последовательность обхода поддерева равна: n7, n5, n6; в это время выполняется обход левого поддерева корневого узла n14, программа возвращается к корневому узлу n14, рекурсивно проходит правое поддерево n14, что в качестве поддерева корневого узла принимает n13. Посредством того же анализа последовательность обхода поддерева For: n13, n12, n11, n9, n10. Мы можем углубить наше понимание этого процесса с помощью алгоритма итеративного обхода, основанного на структуре стека, обсуждаемой ниже.

Если для реализации предварительного обхода двоичного дерева используется нерекурсивный алгоритм, необходима структура стека. Шаги следующие:

Если корневой узел rt пуст, вернитесь; в противном случае сначала поместите корневой узел в стек, а затем итеративно выполните следующие шаги:

1. Вставьте узел n, хранящийся на вершине стека, и посетите этот узел;

2. Вставьте по очереди правый дочерний узел и левый дочерний узел n в стек;

3. Если стек не пуст, вернитесь к шагу 1, чтобы продолжить выполнение, в противном случае завершите итерацию.

Среди них шаг 1 – это операция доступа к узлу; на шаге 2 правый дочерний узел помещается в стек, а затем вставляется левый дочерний узел. Это связано с тем, что всплывающая операция стека подчиняется правилу первого поступления -последнее правило, и корневой узел необходимо посетить после конца. Левый дочерний узел посещается первым, поэтому левый дочерний узел помещается в стек после правого дочернего узла; шаг 3 является условием завершения процесс обхода.

В соответствии с описанными выше итерационными шагами шаги обхода двоичного дерева на рисунке можно разложить на следующие шаги, которые соответствуют шагам, показанным на рисунке.

1. Вставьте n14 в стек;

2. Вставьте верхний узел стека, который в это время равен n14, посетите узел n14;

3. По очереди вставьте в стек правый дочерний узел n13 и левый дочерний узел n8 из n14;

4. Вставьте верхний узел стека, который в это время равен n8, посетите узел n8;

5. По очереди вставьте в стек правый дочерний узел n7 и левый дочерний узел n4 узла n8;

6. Вытяните верхний узел стека, который в это время равен n4, посетите узел n4;

7. Поочередно вставьте в стек правый дочерний узел n3 и левый дочерний узел n2 из n4;

8. Вставьте верхний узел стека, который в это время равен n2, посетите узел n2;

9. Если правый дочерний узел n2 пуст, поместите левый дочерний узел n1 из n2 в стек;

10. Удалите верхний узел стека, который в это время равен n1, посетите узел n1;

11. Если левый дочерний узел n1 пуст, поместите правый дочерний узел n0 из n1 в стек;

12. Вставьте верхний узел стека, который в это время равен n0, посетите узел n0;

13. n0 – листовой узел, дочерние узлы не помещаются в стек;

14. Вытяните верхний узел стека, который в это время равен n3, посетите узел n3;

15. n3 – листовой узел, дочерние узлы не помещаются в стек;

16. Вытяните верхний узел стека, который в это время равен n7, посетите узел n7;

17. По очереди поместите в стек правый дочерний узел n6 и левый дочерний узел n5 узла n7;

18. Удалите верхний узел стека, который в это время равен n5, посетите узел n5;

19. n5 – листовой узел, дочерние узлы не помещаются в стек;

20. Вставьте верхний узел стека, который в это время равен n6, посетите узел n6;

21. n6 – листовой узел, дочерние узлы не помещаются в стек;

двадцать два. Удалите верхний узел стека, который в это время равен n13, посетите узел n13;

двадцать три. Вставьте по очереди правый дочерний узел n11 и левый дочерний узел n12 из n13 в стек;

двадцать четыре. Удалите верхний узел стека, который в это время равен n12, посетите узел n12;

25. n12 – листовой узел, дочерние узлы не помещаются в стек;

26. Вытяните верхний узел стека, который в это время равен n11, посетите узел n11;

27. Поочередно вставьте в стек правый дочерний узел n10 и левый дочерний узел n9 из n11;

28. Вытяните верхний узел стека, который в это время равен n9, посетите узел n9;

29. n9 – листовой узел, дочерние узлы не помещаются в стек;

30. Вставьте верхний узел стека, который в это время равен n10, посетите узел n10;

31. n10 – листовой узел, дочерние узлы не помещаются в стек;

32. Стек пуст, и процесс обхода завершается.

Рисунок Динамический процесс структуры стека алгоритма обхода предварительного порядка двоичного дерева

Структура стека используется в масштабе итераций. Размер стека в проиллюстрированной структуре стека является фиксированным. На самом деле, установить размер стека заранее во время реализации непросто, поэтому в конкретной реализации используйтеГлава XXЦепной стек, обсуждаемый в статье, динамически регулирует размер стека.

Обход по порядку

Второй алгоритм обхода называется алгоритмом обхода по порядку. По сравнению с алгоритмом обхода предварительного заказа, алгоритм обхода среднего порядка сначала посещает левое поддерево узла, затем сам узел и, наконец, правое поддерево узла. Видно, что доступ к самому узлу осуществляется в середине левого и правого поддеревьев, которые Гу называет средним порядком.ФигураРезультатом обхода бинарного дерева по порядку будет:

10→-1→6→4→7→2→8→5→9→1→14→3→12→11→13

Этот процесс можно описать с помощью рекурсивного метода определения: для корневого узла rt, если rt пусто, return, в противном случае рекурсивно пройти левое поддерево rt, затем посетить сам rt и, наконец, пройти правое поддерево rt. следующее:

    rec_inorder(rt){

        1.    if(rt == null) return;

            //Сначала посетите левый дочерний узел
        2.    rec_inorder(rt.getLeft());

            //Затем посетите родительский узел
        3.    Visit(rt);

            //Наконец, посетите правильный дочерний узел
        4.    rec_inorder(rt.getRight());

    }

Во время выполнения сначала обойдите левое поддерево n14, то есть поддерево с n8 в качестве корневого узла, затем продолжите рекурсивный обход левого поддерева n8 до узла n1. В настоящее время левого поддерева n1 нет, поэтому посетить узел n1, а затем пройти по правому поддереву n1, правое поддерево является единственным узлом n0, затем осуществляется прямой доступ к узлу n0. До этого момента обход поддерева с n1 в качестве корневого узла заканчивается, то есть обход левого поддерева с корневым узлом n2 заканчивается, и выполняется посещение узла n2. Так как правое поддерево n2 пусто, обход левого поддерева n4 заканчивается, затем посещается узел n4, а затем проходит правое поддерево n4, то есть поддерево с n3 в качестве корневого узла. один узел, поэтому он напрямую. Посещение узла n3 может закончить обход правого поддерева. В этот момент выполняется обход левого поддерева узла n8 и посещение узла n8. Тот же метод может анализировать процесс обхода правого поддерева узла n8, и порядок обхода узлов в поддереве следующий: n5, n7, n6. После завершения обхода поддерева с n8 в качестве корневого узла, сначала посетите узел n8, а затем рекурсивно вызовите алгоритм обхода по порядку для доступа к правому поддереву узла n14, то есть поддереву с n13 в качестве корневого узла Используя тот же процесс анализа, мы видим, что последовательность обхода этого поддерева: n12, n13, n9, n11, n10.

Когда для реализации обхода по порядку используется итерационный алгоритм, процесс отличается от итеративного процесса предыдущего обхода. В алгоритме предварительного обхода, когда поддерево узла продолжает посещаться после посещения узла, сначала посещается корневой узел поддерева. Следовательно, в итеративном алгоритме каждый раз, когда мы посещаем узел, нам нужно только Два дочерних узла проталкивают стек, а затем итеративно выталкивают верхний узел стека и посещают этот узел. Однако в процессе обхода среднего порядка сначала посещается левое поддерево узла, и он рекурсивно продолжается до тех пор, пока левое поддерево определенного узла не станет пустым, как показано на рисунке, до узла n1. В этом процессе необходимо записать корневой узел каждого левого поддерева, то есть n14, n8, n4, n2, n1 помещаются в стек. Затем по очереди откройте узел и посетите его, а затем, чтобы пройти по правому поддереву узла, вам также необходимо итеративно нажать левый дочерний узел правого поддерева узла, как показано на рисунке. Шаги этого процесса следующие:

Если корневой узел rt пуст, вернитесь; в противном случае сначала нажмите корневой узел rt и итеративно нажмите левый дочерний узел корневого узла и левый дочерний узел левого дочернего узла, а затем итеративно выполните следующие шаги:

1. Поднимите верхний узел n стека и посетите этот узел;

2. Если правый дочерний узел n не пуст, поместите правый дочерний узел rgt в стек и итеративно вставьте левый дочерний узел rgt и левый дочерний узел левого дочернего узла в стек;

3. Если стек не пуст, вернитесь к шагу 1, чтобы продолжить выполнение, в противном случае завершите итерацию.

Шаг 1 – операция доступа к узлу; на шаге 2 сначала определите, является ли правый дочерний узел всплывающего узла на вершине стека пустым узлом, если он не пуст, вставьте правый дочерний узел в стек , а затем итеративно помещает левый дочерний узел в стек; 3 – это условие завершения процесса обхода.

Рисунок Итерационный процесс по порядку

Сначала вставьте корневой узел в стек и итеративно вставьте левые дочерние узлы n8, n4, n2, n1 в стек; после посещения узла n8 поместите корневой узел n7 его правого поддерева в стек и итеративно вставьте его левый дочерний узел Stack.

Согласно описанным выше шагам итерации, процесс итерации двоичного дерева на рисунке таков:

1. Вставьте узлы n14, n8, n4, n2, n1 в стек по очереди;

2. Удалите верхний узел стека, который в это время равен n1, посетите n1;

3. Вставьте в стек правый узел n0 из n1. Поскольку левый дочерний узел n0 пуст, итеративного процесса проталкивания нет;

4. Вставьте верхний узел стека, который в это время равен n0, посетите n0;

5. N0 – листовой узел, ни один узел не помещается в стек;

6. Удалите верхний узел стека, который в это время равен n2, посетите n2;

7. Правый узел n2 пуст, и ни один узел не помещается в стек;

8. Вытяните верхний узел стека, который сейчас равен n4, посетите n4;

9. Вставьте в стек правый узел n3 из n4. Поскольку левый дочерний узел n3 пуст, итеративного процесса проталкивания нет;

10. Вытащите верхний узел стека, который в это время равен n3, посетите n3;

11. n3 – листовой узел, ни один узел не помещается в стек;

12. Вытяните верхний узел стека, который сейчас равен n8, и посетите n8;

13. Вставьте правый дочерний узел n7 из n8 в стек и поместите узел n5 в стек;

14. Вытяните верхний узел стека, который в это время равен n5, посетите n5;

15. n5 – листовой узел, ни один узел не помещается в стек;

16. Вытяните верхний узел стека, который в это время равен n7, посетите n7;

17. Вставьте в стек правый узел n6 из n7. Поскольку левый дочерний узел n6 пуст, итеративного процесса выталкивания нет;

18. Вытяните верхний узел стека, который в это время равен n6, посетите n6;

19. n6 – листовой узел, ни один узел не помещается в стек;

20. Вставьте верхний узел стека, который в это время равен n14, посетите узел n14;

21. Вставьте правый узел n13 из n14 в стек и вставьте узел n12 в стек;

двадцать два. Поднимите верхний узел стека, который в это время равен n12, посетите n12;

двадцать три. n12 – листовой узел, ни один узел не помещается в стек;

двадцать четыре. Удалите верхний узел стека, который в это время равен n13, посетите узел n13;

25. Вставьте правый узел n11 из n13 в стек и вставьте n9 в стек;

26. Вытяните верхний узел стека, который в это время равен n9, посетите n9;

27. n9 – листовой узел, поэтому ни один узел не помещается в стек;

28. Вытяните верхний узел стека, который в это время равен n11, посетите n11;

29. Вставить правый узел n10 из n11 в стек, а n10 – листовой узел, без итеративного процесса проталкивания;

30. Вставьте верхний узел стека, который в это время равен n10, посетите узел n10;

31. n10 – листовой узел, ни один узел не помещается в стек;

32. Стек пуст, и итерационный процесс завершается.

Рисунок Динамический процесс структуры стека итеративного алгоритма обхода среднего порядка двоичного дерева

Пост-заказ обход

Порядок обхода после заказа противоположен порядку обхода перед порядком. Во время обхода перед порядком сначала посещается родительский узел, а при обходе пост-заказа родительский узел посещается последним. Рекурсивный алгоритм обхода после порядка очень похож на рекурсивный алгоритм обхода до и среднего порядка.Мы не будем обсуждать его здесь подробно, а в основном обсудим итерационный алгоритм обхода после порядка.

В процессе обхода пост-порядка сначала обходится левое поддерево узла, что совпадает с первым шагом обхода среднего порядка. Следовательно, в итеративной реализации процесс инициализации стека состоит в том, чтобы поместить корневой узел дерева в стек и итеративно протолкнуть левый дочерний узел корневого узла и левый дочерний узел левого дочернего узла в стек. . Разница в том, что следующий шаг – не вытолкнуть верхний узел стека и не посетить его, потому что посещение узла должно быть выполнено после обхода правого поддерева узла. Следовательно, правильная операция должна сначала прочитать верхний узел стека (а не вытолкнуть верхний узел стека). Следующий алгоритм аналогичен итерационному алгоритму обхода по порядку: если правый дочерний узел не пуст, сначала вставьте правый узел rgt узла в стек, а затем итеративно поместите левый дочерний узел rgt в стек; если правый дочерний узел узла – это пустой узел, вытолкните верхний узел стека и получите к нему доступ. Но с этим процессом есть большая проблема, давайте обсудим этот процесс на примере. На рисунке показано поддерево на рисунке.

Поддерево (a) (b) (c)

Рисунок. Анализ итерационного алгоритма обхода двоичного дерева после заказа.

Как показано на рисунке, элементами в стеке являются узлы n2 и n1, а узел n1 находится наверху стека, как показано на рисунке (a). В соответствии с шагами, которые мы обсуждали выше, сначала прочтите узел n1 и поместите его правый дочерний узел n0 в стек. Поскольку n0 является листовым узлом, итеративной операции push нет. В это время верхним узлом стека является n0, поскольку показано на рисунке (b). Затем снова прочитайте верхний узел n0 стека.Поскольку в n0 нет узла, вытолкните верхний узел n0 стека, как показано на рисунке (c), и посетите узел. В это время узлы в стеке такие же, как в (a), и процесс итерации по-прежнему выполняется в соответствии с вышеуказанными шагами, которые превратятся в бесконечный цикл.

После того, как обход левого поддерева узла здесь заканчивается, родительский узел должен оставаться в стеке и ждать завершения обхода правого поддерева, прежде чем он будет извлечен из стека; после завершения обхода правого поддерева родительский узел должен быть извлечен из стека, но вопрос в том, как отличить конец обхода левого поддерева или конец обхода правого поддерева, и вытолкнуть родительский узел из стека, когда заканчивается обход правого поддерева?

Внимательно наблюдая за процессом обхода после заказа, мы можем обнаружить, что для родительского узла в конце обхода левого поддерева последний посещенный узел является левым дочерним узлом родительского узла. Аналогичным образом, в конце правого обход поддерева. Наиболее посещаемым узлом является правый дочерний узел родительского узла. В соответствии с этим правилом мы можем разработать указатель узла last_visited так, чтобы он указывал на последний посещенный узел и оценивал, совпадает ли он с правым дочерним узлом родительского узла. Если они совпадают, это означает, что обход правого поддерева узла завершен, и затем следует открыть верхний узел стека и получить к нему доступ. Мы можем еще раз обсудить пример на рисунке:

На рисунке (a) ни один узел не был посещен в это время, то есть last_visited пуст, поэтому last_visited не то же самое, что правый дочерний узел n1, и верхний узел стека читается напрямую; на рисунке ( c) узел n0 выталкивается и посещается. В это время last_visited ← n0, в это время last_visited равен правому дочернему узлу n1, что указывает на доступ к правому поддереву n1, поэтому следующим шагом должно быть открытие и посетите верхний узел n1.

В соответствии с приведенным выше обсуждением этапы итерационной реализации алгоритма последующего обхода двоичного дерева следующие:

1. Считайте верхний узел стека n. Если правый дочерний узел узла не пуст и правый дочерний узел не совпадает с последним посещенным узлом last_visited, поместите правый дочерний узел узла в стек и итеративно толкает левый дочерний узел правого дочернего узла Дочерний узел помещается в стек;

2. Если правый дочерний узел узла n пуст или правый дочерний узел совпадает с последним посещенным узлом last_visited, выскакивает верхний узел n стека, посещает узел и обновляет последний посещенный узел last_visited до узла n ;

3. Если стек не пуст, вернитесь к шагу 1 и продолжите, иначе итерация завершится;

На шаге 1 выше прочтите верхний узел стека, не посещайте узел напрямую, а сначала определите, было ли пройдено правое поддерево узла, если нет, то итеративно нажмите правый дочерний узел и левый дочерний узел узел в стеке; если было пройдено правое поддерево узла, вытолкнуть верхний узел стека напрямую и получить к нему доступ; третий шаг является условием завершения итерационного процесса.

Чтобы подробнее описать вышеупомянутые шаги, мы все еще используемНа картинкеВозьмите двоичное дерево в качестве примера для дальнейшего объяснения каждого шага:

1. Вставьте по очереди узлы n14, n8, n4, n2, n1 в стек, last_visited = NULL;

2. Считайте верхний узел стека, n1, правый узел узла не пуст и отличается от last_visited, затем правый дочерний узел n0 из n1 помещается в стек, n0 – листовой узел, и есть нет итеративного процесса проталкивания;

3. Считайте верхний узел стека, n0, правый узел узла пуст, затем вытяните верхний узел n0 стека, посетите узел n0 и last_visited ← n0;

4. Считайте верхний узел стека, n1, в это время правый дочерний узел n1 такой же, как last_visited, затем выскочите верхний узел n1 стека, посетите узел n1 и last_visited ← n1;

5. Считайте верхний узел стека, n 2. В это время правый дочерний узел n2 пуст, затем выскакивает верхний узел n2, посещает узел n2 и last_visited ← n2;

6. Считайте верхний узел стека, n4. В это время правый дочерний узел n4 не пуст и отличается от last_visited, затем правый дочерний узел n3 из n4 помещается в стек, n3 – листовой узел. , и нет итеративного процесса push;

7. Считайте верхний узел стека, n3, в это время правый дочерний узел n3 пуст, затем выскочите верхний узел стека, посетите узел n3 и last_visited ← n3;

8. Считайте верхний узел стека, n4, в это время правый дочерний узел n4 такой же, как last_visited, затем выскочите верхний узел n4, посетите узел n4 и last_visited ← n4;

9. Считайте верхний узел стека, n8. В это время правый дочерний узел n8 не пуст и отличается от last_visited, затем вставьте правый дочерний узел n7 из n8 в стек и итеративно нажмите левый дочерний узел. узел n5 из n7 в стек

10. Считайте верхний узел стека, n 5. В это время правый дочерний узел n5 пуст, затем выскакивает верхний узел стека, посещает узел n5 и last_visited ← n5;

11. Считайте верхний узел стека, n7. В это время правый дочерний узел n7 не пуст и отличается от last_visited, затем правый дочерний узел n6 из n7 помещается в стек, n6 – листовой узел , и нет итеративного процесса push;

12. Считайте верхний узел стека, n 6. В это время правый дочерний узел n6 пуст, затем выскакивает верхний узел стека, посещает узел n6 и last_visited ← n6;

13. Считайте верхний узел стека, n 7. В это время правый дочерний узел n7 совпадает с last_visited, затем выскакивает верхний узел n7, посещает узел n7 и last_visited ← n7;

14. Считайте верхний узел стека, n8, в это время правый дочерний узел n8 такой же, как last_visited, затем вставьте верхний узел n8 стека, посетите узел n8 и last_visited ← n8;

15. Считайте верхний узел стека, n14. В это время правый дочерний узел n14 не пуст и отличается от last_visited, затем правый дочерний узел n13 из n14 помещается в стек, а левый дочерний узел n12 из n13 итеративно помещается в стек ；

16. Считайте верхний узел стека, n12, в это время правый дочерний узел n12 пуст, выскочите верхний узел стека, посетите узел n12 и last_visited ← n12;

17. Считайте верхний узел стека, n13. В это время правый дочерний узел n13 не пуст и отличается от last_visited, затем вставьте правый дочерний узел n11 из n13 в стек и итеративно протолкните левый дочерний узел узел n9 из n11 в стек ；

18. Считайте верхний узел стека, n9, в это время правый дочерний узел n9 пуст, затем выскочите верхний узел стека, посетите узел n9 и last_visited ← n9;

19. Считайте верхний узел стека, n11. В это время правый дочерний узел n11 не пуст и отличается от last_visited, затем правый дочерний узел n10 из n11 помещается в стек, n10 – листовой узел , и нет итеративного процесса push;

20. Считайте верхний узел стека, n13, в это время правый дочерний узел n13 такой же, как last_visited, затем выскочите верхний узел стека, посетите узел n13 и last_visited ← n13;

21. Считайте верхний узел стека n 14. В это время правый дочерний узел n14 совпадает с last_visited, затем выскакивает верхний узел n14, посещает узел n14 и last_visited ← n14;

22. В настоящее время в стеке нет узлов, и процесс итерации завершается.

Рисунок Итерационный алгоритм обхода после заказа реализует процесс динамического изменения стека.

Из итеративного процесса можно обнаружить, что, в отличие от итерационных алгоритмов обхода предварительного заказа и обхода среднего порядка, в процессе обхода предварительного заказа и обхода среднего порядка каждая итерация выталкивает верхний узел стека, затем посещает узел и вносит соответствующие корректировки; но в итеративном алгоритме обхода после заказа на каждой итерации не требуется определять атрибуты верхнего узла стека. В некоторых случаях верхний узел стека может быть вытянут напрямую, в то время как в других случаях верхний узел стека не может быть извлечен напрямую, и необходимо вставить новый узел в стек. Таким образом, интуитивно мы также можем обнаружить, что итеративный алгоритм обхода пост-заказа имеет больше операций в стеке, чем обходы предварительного и среднего порядка.

Обход последовательности

Последний общий алгоритм обхода называется алгоритмом обхода последовательности слоев. Этот алгоритм более интуитивно понятен, чем предыдущие три алгоритма. Его обход выполняется в порядке количества слоев узлов, появляющихся в порядке возрастания, а узлы на каждом уровне в порядке слева направо. Заходите вправо. НапримерНа картинкеПорядок обхода двоичного дерева:

Уровень 0: n14;

Первый слой: n8, n13;

Второй слой: n4, n7, n12, n11;

…… ……

Процесс обхода последовательности слоев не подходит для выполнения рекурсивными алгоритмами.Мы специально анализируем следующие законы обхода последовательности слоев и надеемся найти подходящий алгоритм для решения обхода последовательности слоев.

Уровень 0: корневой узел n14;

Уровень 1. Оба узла n8 и n13 являются дочерними узлами узла n14;

Уровень 2: оба узла n4 и n7 являются дочерними узлами узла n8, и оба узла n12 и n11 являются дочерними узлами узла n13;

Уровень 3: узлы n2 и n3 являются дочерними узлами узла n4, n5 и n6 являются дочерними узлами узла n7, n9 и n10 являются дочерними узлами узла n11, а n12 на втором уровне не имеет дочерних узлов на третьем уровне;

Уровень 4: Узел n1 является дочерним узлом n2;

Уровень 5: Узел n0 является дочерним узлом n1;

Можно обнаружить, что после посещения узла n14 на 0-м уровне следующие два дочерних узла n14 должны быть посещены; первый уровень посетил n8 и n13, а два дочерних узла n8 должны быть посещены на втором уровне. , а затем необходимо посетить дочерний узел n13. node …….

Как показаноДля этого процесса проанализируйте процесс доступа к каждому узлу, спроектируйте линейную таблицу, сначала сохраните n14, как показано на (a); затем выньте его из заголовка таблицы и добавьте два его дочерних узла в конец таблицы. таблица, такая как на рисунке (b); Затем повторяйте этот процесс, каждый раз, когда головной узел извлекается и посещает узел, в то же время, если узел имеет дочерние узлы, добавьте дочерние узлы узла в конец таблица, если узел не имеет дочерних узлов. Узел не добавляется.

Далее проанализируйте линейную таблицу, упомянутую выше, при добавлении узла в таблицу, узел добавляется в конец линейной таблицы, и каждый раз, когда узел удаляется из таблицы, узел берется из заголовка таблицы. Это рабочее правило – правило «первым пришел – первым обслужен»,Глава XXXОчереди, обсуждаемые в разделе, соответствуют этому правилу. Согласно вышеприведенному анализу, обход последовательности может быть достигнут с помощью очередей. Шаги следующие:

Если корневой узел rt пуст, вернитесь, в противном случае создайте очередь и добавьте корневой узел двоичного дерева и итеративно выполните следующие шаги:

1. Выньте головной узел n очереди и посетите этот узел;

2. Если левый дочерний узел узла n не пуст, добавьте левый дочерний узел в очередь; если правый дочерний узел узла n не пуст, добавьте правый дочерний узел в очередь;

3. Если очередь не пуста, вернитесь к шагу 1, чтобы продолжить итерацию, в противном случае итерация завершится.

Рисунок Принципиальная схема процесса обхода последовательности двоичного дерева

Реализация четырех алгоритмов обхода

Основываясь на приведенном выше обсуждении четырех алгоритмов обхода, мы можем разработать структуру данных двоичного дерева на основе класса узла двоичного дерева следующим образом:

Код:

package Tree;

import Element.ElemItem;

import Queue.LinkQueue;

import Stack.LinkStack;

/**
  *
* Класс двоичного дерева, LinkBinTree.java
* В основном включает предварительный заказ двоичного дерева, последующий заказ, средний порядок и порядок слоев
* Рекурсивная и нерекурсивная реализация алгоритма обхода
  */

public class LinkBinTree {

     //Частная переменная
     private LinkBinTreeNode root;//корень//Конструктор без параметров
     public LinkBinTree(){

         root = null;

     }

     //Конструктор с параметрами
     public LinkBinTree(LinkBinTreeNode _root){

         root = _root;

}

     //Обход предзаказа
     public void rec_preorder(LinkBinTreeNode rt){

         if(rt == null) return;

         //Сначала посетите родительский узел
         System.out.print(rt + “→”);

         //Затем посетите левый дочерний узел
         rec_preorder(rt.getLeft());

         //Последнее посещение правого дочернего узла
         rec_preorder(rt.getRight());

     }

     //Итерационный метод достижения обхода предварительного заказа
     public void itr_preorder(LinkBinTreeNode rt){

         if(rt == null) return;

         //Создать структуру данных цепного стека
         LinkStack ls = new LinkStack();

         //Сначала поместите корневой узел в стек
         ls.push(new ElemItem<LinkBinTreeNode>(rt));

         //Продолжайте появляться и посещать, нажимая левый и правый дочерние узлы
         while(ls.getSize() != 0){

             rt = (LinkBinTreeNode)(ls.pop().getElem());

             //Посетите корневой узел
             System.out.print(rt + “→”);

             if(rt.getRight() != null)

                 //Нажмите правый дочерний узел
                 ls.push(new

                    ElemItem<LinkBinTreeNode>(rt.getRight())

                   );

             if(rt.getLeft() != null)

                 //Нажмите левый дочерний узел
                 ls.push(new

                    ElemItem<LinkBinTreeNode>(rt.getLeft())

                   );

         }

     }

     //Рекурсивный метод для выполнения обхода после заказа
     public void rec_postorder(LinkBinTreeNode rt){

         if(rt == null) return;

         //Сначала посетите левый дочерний узел
         rec_postorder(rt.getLeft());

         //Затем посетите правый дочерний узел
         rec_postorder(rt.getRight());

         //Последнее посещение родительского узла
         System.out.print(rt + “→”);

     }

     //Итерационный метод для выполнения обхода после заказа
     public void itr_postoder(LinkBinTreeNode rt){

         if(rt == null) return;

         //Создайте объект узла для кэширования родительского узла
         LinkBinTreeNode p = new LinkBinTreeNode();

         //Создайте связанный объект стека
         LinkStack ls = new LinkStack();

         //Создайте узел для кеширования ранее посещенного (правого) узла
         LinkBinTreeNode t = new LinkBinTreeNode();

         //Итеративно помещайте узел и левый дочерний узел узла в стек
         while(rt != null){

             ls.push(new ElemItem<LinkBinTreeNode>(rt));

             rt = rt.getLeft();

         }

         //Обработка вне стека
         while(ls.getSize() > 0){

             //Получить верхний элемент стека
             rt = (LinkBinTreeNode)(ls.getTop().getElem());

             //Если правый узел элемента не пуст, а правый дочерний узел узла
             //Итеративно помещайте правый дочерний узел и его левый дочерний узел в стек, если он не был посещен
             if(rt.getRight() != null &&

                 rt.getRight() != t){

                 rt = rt.getRight();

                 while(rt != null){

                     ls.push(new

                        ElemItem<LinkBinTreeNode>(rt)

                       );

                     rt = rt.getLeft();

                 }

             }

             //Если правый дочерний узел пуст, узел появится и распечатает (посетит)
             else{

                 rt = (LinkBinTreeNode)(ls.pop().getElem());

                 System.out.print(rt + “→”);

                 t = rt;

             }

         }

     }

     //Обход по порядку
     public void rec_inorder(LinkBinTreeNode rt){

         if(rt == null) return;

         //Сначала посетите левый дочерний узел
         rec_inorder(rt.getLeft());

         //Затем посетите родительский узел
         System.out.print(rt + “→”);

         //Наконец, посетите правильный дочерний узел
         rec_inorder(rt.getRight());

}

     //Итерационный алгоритм для упорядоченного доступа
     public void itr_inorder(LinkBinTreeNode rt){

         if(rt == null) return;

         //Создать структуру данных цепного стека
         LinkStack ls = new LinkStack();

         //Итеративно помещайте левый дочерний узел rt в стек
         while(rt != null){

             ls.push(new ElemItem<LinkBinTreeNode>(rt));

             rt = rt.getLeft();

         }

         //Траверс
         while(ls.getSize() > 0){

             //Вытащить верхний узел стека
             rt = (LinkBinTreeNode)(ls.pop().getElem());

             //Посетить узел
             System.out.print(rt + “→”);

             //Если правый дочерний узел узла не пуст,
             //Вставьте правый узел и все его левые дочерние узлы в стек
             if(rt.getRight() != null){

                 ls.push(new

                     ElemItem<LinkBinTreeNode>(rt.getRight())

                    );

                 //Итеративно помещайте левый дочерний узел в стек
                 rt = rt.getRight().getLeft();

                 while(rt != null){

                     ls.push(new

                         ElemItem<LinkBinTreeNode>(rt)

                        );

                     rt = rt.getLeft();

                 }

             }

         }

}

     //Последовательная печать
     public void layer_order(LinkBinTreeNode rt){

         //Создать очередь
         LinkQueue lq = new LinkQueue();

         lq.enqueue(new ElemItem<LinkBinTreeNode>(rt));

         while(lq.currSize() > 0){

             //Dequeue
             rt = (LinkBinTreeNode)(lq.dequeue().getElem());

             //Посетите головной узел очереди
             System.out.print(rt + “→”);

             if(rt.getLeft() != null)

                 //Сохранить левый дочерний узел узла в очередь
                 lq.enqueue(new

                   ElemItem<LinkBinTreeNode>(rt.getLeft()));

             if(rt.getRight() != null)

                 //Сохраните правый дочерний узел узла в очередь
                 lq.enqueue(new

                   ElemItem<LinkBinTreeNode>(rt.getRight()));

         }

     }

     //Получите корневой узел
     public LinkBinTreeNode getRoot(){

         return root;

     }

}

В предыдущей главе, когда мы обсуждали максимальную кучу, мы упоминали, что структура кучи – это особое двоичное дерево, то есть полное двоичное дерево. Учитывая набор сопоставимых узлов (наследующих класс Comparable), их можно создать в максимальной куче. Но в классе двоичного дерева, разработанном здесь, есть только одна переменная-член в корневом узле, и между узлами нет конкретной связи. Это обобщенное двоичное дерево. Затем мы используем примеры программ для проверки различных алгоритмов обхода двоичного дерева.

package Tree;

import Element.ElemItem;

/**
*
*
* Проверьте функцию обхода двоичного дерева:
* 1. Два алгоритма обхода предварительного заказа.
* 2. Два алгоритма обхода постзаказов.
* 3. Два алгоритма обхода среднего порядка.
* 4. Алгоритм обхода последовательности
*/

public class ExampleLinkBinTree {

    public static void main(String args[]){

        //Создание двоичного дерева
        LinkBinTreeNode n0 =

            new LinkBinTreeNode(new ElemItem<Integer>(-1),

                                null, null);

        LinkBinTreeNode n1 =

            new LinkBinTreeNode(new ElemItem<Integer>(10),

                                null, n0);

        LinkBinTreeNode n2 =

            new LinkBinTreeNode(new ElemItem<Integer>(6),

                                n1, null);

        LinkBinTreeNode n3 =

            new LinkBinTreeNode(new ElemItem<Integer>(7),

                                null, null);

        LinkBinTreeNode n4 =

            new LinkBinTreeNode(new ElemItem<Integer>(4),

                                n2, n3);

        LinkBinTreeNode n5 =

            new LinkBinTreeNode(new ElemItem<Integer>(8),

                                null, null);

        LinkBinTreeNode n6 =

            new LinkBinTreeNode(new ElemItem<Integer>(9),

                                null, null);

        LinkBinTreeNode n7=

            new LinkBinTreeNode(new ElemItem<Integer>(5),

                                n5, n6);

        LinkBinTreeNode n8 =

            new LinkBinTreeNode(new ElemItem<Integer>(2),

                                n4, n7);

        LinkBinTreeNode n9 =

            new LinkBinTreeNode(new ElemItem<Integer>(12),

                                null, null);

        LinkBinTreeNode n10 =

            new LinkBinTreeNode(new ElemItem<Integer>(13),

                                null, null);

        LinkBinTreeNode n11 =

            new LinkBinTreeNode(new ElemItem<Integer>(11),

                                n9, n10);

        LinkBinTreeNode n12 =

            new LinkBinTreeNode(new ElemItem<Integer>(14),

                                null, null);

        LinkBinTreeNode n13 =

            new LinkBinTreeNode(new ElemItem<Integer>(3),

                                n12, n11);

        LinkBinTreeNode n14 =

            new LinkBinTreeNode(new ElemItem<Integer>(1),

                                n8, n13);

        LinkBinTree lbt = new LinkBinTree(n14);

        //Два предварительных теста
System.out.println (“\ n рекурсивный алгоритм для достижения обхода предварительного заказа:”);

        lbt.rec_preorder(lbt.getRoot());

System.out.println (“\ nИтеративный алгоритм для достижения обхода предварительного заказа:”);

        lbt.itr_preorder(lbt.getRoot());

        //Два промежуточных теста
System.out.println (“\ n рекурсивный алгоритм для достижения обхода среднего порядка:”);

        lbt.rec_inorder(lbt.getRoot());

System.out.println (“\ nИтеративный алгоритм для достижения обхода по порядку:”);

        lbt.itr_inorder(lbt.getRoot());

        //Два последующих теста
System.out.println (“\ n рекурсивный алгоритм для достижения обхода после заказа:”);

        lbt.rec_postorder(lbt.getRoot());

System.out.println (“\ nИтеративный алгоритм для достижения обхода после заказа:”);

        lbt.itr_postoder(lbt.getRoot());

        //Последовательный тест
System.out.println (“\ nИтеративный алгоритм для достижения обхода последовательности слоев:”);

        lbt.layer_order(lbt.getRoot());

    }

}

В программе-примере сначала создайте двоичное дерево, его структуру и узлы.Как показано, Выполните обход предварительного заказа, обход среднего порядка и обход после порядка с помощью рекурсивных и итерационных алгоритмов соответственно, и используйте итерационный метод для достижения обхода последовательности слоев. Результаты следующие:

Рекурсивный алгоритм реализует обход предварительного порядка:

1→2→4→6→10→-1→7→5→8→9→3→14→11→12→13→

Итерационный алгоритм для достижения обхода предзаказа:

1→2→4→6→10→-1→7→5→8→9→3→14→11→12→13→

Рекурсивный алгоритм для выполнения обхода по порядку:

10→-1→6→4→7→2→8→5→9→1→14→3→12→11→13→

Итерационный алгоритм для достижения обхода по порядку:

10→-1→6→4→7→2→8→5→9→1→14→3→12→11→13→

Рекурсивный алгоритм реализует обход постзаказа:

-1→10→6→7→4→8→9→5→2→14→12→13→11→3→1→

Итерационный алгоритм реализует обход постзаказа:

-1→10→6→7→4→8→9→5→2→14→12→13→11→3→1→

Итерационный алгоритм обхода последовательности слоев:

1→2→3→4→5→14→11→6→7→8→9→12→13→10→-1→

резюме

В первых четырех разделах мы в основном обсуждали свойства бинарных деревьев, которые в основном недоступны в обобщенной древовидной структуре из-за ограниченной структуры бинарных деревьев. Кроме того, обсуждаются четыре алгоритма обхода бинарных деревьев, обсуждаются итерационная и неитеративная реализации обхода предварительного, среднего и пост-порядка соответственно, а также обсуждается метод реализации алгоритма обхода последовательности слоев. Эти алгоритмы обхода также подходят для структур с определенными отношениями между узлами, такими как максимальная куча и двоичное дерево поиска, которые будут обсуждаться в следующих главах.

Дерево кодирования Хаффмана

Кодирование Хаффмана – это метод кодирования переменной длины, созданный американским математиком Дэвидом Хаффманом, и представляет собой специальную форму преобразования двоичного дерева. Идея кодирования заключается в преобразовании часто используемых кодов в более короткие кодовые слова (обычно кодовые слова типа 0–1 бит), в то время как те, которые используются реже, могут использовать более длинные кодовые слова и сохранять уникальность кода.

Кодирование Хаффмана применялось во многих важных областях сжатия данных, и теоретической основой технологии сжатия данных является теория информации. Согласно принципу теории информации, можно найти лучший метод кодирования сжатия данных.Теоретическим пределом сжатия данных является энтропия информации. Если требуется, чтобы количество информации не было потеряно в процессе кодирования, то есть требуется сохранение энтропии информации.Это кодирование с сохранением информации также называется кодированием с сохранением энтропии или энтропийным кодированием. С точки зрения теории информации, кодирование Хаффмана – это энтропийное кодирование.

Самый фундаментальный принцип алгоритма Хаффмана: длина взвешенного пути дерева Хаффмана является наименьшей. Так называемая взвешенная длина пути дерева записывается как WPL = W1 * L1 + W2 * L2 + W3 * L3 + … + Wn * Ln, n представляет количество конечных узлов двоичного дерева Хаффмана. Wi (i = 1,2, …, n) представляет n весов, а Li (i = 1,2, …, n) представляет количество слоев n листовых узлов или длину пути.

Конкретные шаги кодирования Хаффмана на n исходных информационных символах резюмируются следующим образом:

1. Статистика вероятностей, получить различные вероятности n символов;

2. Отсортируйте n вероятностей n исходных информационных символов в порядке возрастания вероятности;

3. Добавьте две последние малые вероятности среди n вероятностей, а затем уменьшите количество значений вероятности до n-1;

4. Измените порядок вероятностей n-1 в соответствии с их размером;

5. Повторите 3, чтобы сложить последние две малые вероятности после новой сортировки, а затем отсортируйте сумму с оставшимися вероятностями;

6. Повторите это n-2 раза и получите только две вероятностные последовательности;

7. Назначьте значения с элементами двоичного кода (0-1), чтобы сформировать кодовые слова Хаффмана, и кодирование завершится.

Следующий пример дополнительно поясняет процесс этапов кодирования Хаффмана 1 ~ 6. Для информационных символов источника a1, a2, a3, a4, a5, a6, a7 статистическая вероятность равна:

P(a1)=0.2，P(a2)=0.19，P(a3)=0.18，

P(a4)=0.17，P(a5)=0.15，P(a6)=0.1，P(a7)=0.01。

Процесс кодирования Хаффмана для символа исходной информации:

1. По значению вероятности информационного символа выполните сортировку от малого к большему, и результат после сортировки будет:

2. Объедините a7 и a6 в промежуточный узел, пометьте промежуточный узел суммой значений вероятности двух и замените a7 и a6 промежуточным узлом. Результат после переупорядочения:

Можно обнаружить, что, хотя значение вероятности промежуточного узла является суммой a7 и a6, его значение все еще является наименьшим, и нет необходимости корректировать последовательность.

3. Продолжайте объединять узлы 0.11 и a5 в промежуточный узел, пометьте узел суммой значений вероятности 0.11 и a5, и результат после переупорядочения будет:

В это время значение вероятности промежуточного узла больше, чем значение вероятности любого другого узла, и требуется корректировка последовательности.

4. Объедините a4 и a3 в промежуточные узлы и настройте порядок, результат:

5. Объедините a2 и a1 в промежуточные узлы, отрегулируйте порядок, и результат будет:

6. Объедините промежуточные узлы 0,26 и 0,35 и измените порядок, и результат будет:

7. Наконец, узлы 0,39 и 0,61 объединяются для получения дерева Хаффмана:

Реализация древовидной структуры Хаффмана

Затем мы сначала обсудим реализацию дерева Хаффмана, а затем обсудим использование и свойства дерева Хаффмана для кодирования Хаффмана.

Дерево Хаффмана – это специальное двоичное дерево. Структура данных двоичного дерева обсуждалась в предыдущей части этой главы. Здесь мы сначала анализируем структуру данных содержимого узла дерева Хаффмана.

Из приведенного выше примера можно обнаружить, что конечные узлы установленного дерева Хаффмана содержат информационные символы и значения вероятности, а промежуточные узлы не имеют информационных символов, только значения вероятности, и его значение представляет собой сумму значений вероятности двух дочерних узлов. Вы можете проектировать структуры данных для конечных и промежуточных узлов по отдельности. Более эффективный метод – разработать унифицированную структуру данных и определить информационный символ промежуточного узла как недопустимый информационный символ «□».

Кроме того, в процессе построения дерева Хаффмана необходимо настроить порядок узлов, что требует сопоставимости между узлами. Объектом сравнения является значение вероятности узла, которое может быть реализовано путем наследования интерфейса Comparable. .

Согласно вышеприведенному обсуждению, дизайн класса содержимого узла дизайна:

package Tree;

/**
*
*
* В кодировании Хаффмана типом узла дерева является пара строки и ее частоты.
* HuffmanPair.java
*/

public class HuffmanPair implements Comparable{

    //Два закрытых участника
    //Нить
    private String c;

    //Частота, соответствующая струне
    private double freq;

    //Конструктор без параметров
    public HuffmanPair(){

        c = “□”;

        freq = -1;

    }

    //Конструктор с параметрами
    public HuffmanPair(String _c,

                    double _f){

        c = _c;

        freq = _f;

    }

    //Установить строковые переменные-члены
    public void setChar(String _c){

        c = _c;

    }

    //Установите частотную переменную строки
    public void setFreq(double _f){

        freq = _f;

    }

    //Получить строковую переменную-член
    public String getChar(){

        return c;

    }

    //Частота получения строки
    public double getFreq(){

        return freq;

    }

    //Реализуйте интерфейсные функции, сравните частоту текущего объекта с другим объектом
    public int compareTo(Object arg0) {

        //Текущий объект маленький, верните -1
        if( freq < ((HuffmanPair)(arg0)).freq)

            return -1;

        //Текущий объект большой, верните 1
        else if(freq > ((HuffmanPair)(arg0)).freq)

            return 1;

        //равный
        else

            return 0;

    }

    //Возвращает строковую форму текущего содержимого узла Хаффмана
    public String toString(){

        return “–” + c + ” ” + freq;

    }

}

Класс содержимого узла дерева Хаффмана, класс HuffmanPair, содержит две закрытые переменные-члены: переменная строкового типа c представляет информационный символ, а переменная двойной точности freq представляет частоту информационного символа. Конструктор без параметров присваивает c недопустимому информационному символу «□». Последняя функция compareTo реализует структурную функцию Comparable. Сравниваются два объекта класса HuffmanPair и сравниваются их значения частоты. Если значение частоты текущего объекта больше, оно возвращает 1, а если оно меньше, оно возвращает -1, возвращает 0, если равно. Чтобы облегчить отображение содержимого узла, класс включает функцию toString, которая возвращает информационный символ и значение частоты информационного символа.

Узлы дерева Хаффмана HuffmanTree используют объекты класса узла двоичного дерева LinkBinTreeNode, разработанные в предыдущих разделах, а элементы узловых элементов при их использовании являются объектами класса HuffmanPair. Иерархические отношения:

    HuffmanTree

        LinkBinTreeNode

            HuffmanPair

                String

                double

Построение дерева Хаффмана начинается с массива типа LinkBinTreeNode, а содержимое узла, содержащееся в каждом элементе массива типа LinkBinTreeNode, имеет тип HuffmanPair. Пусть массив будет hufflist и его длина равна n.

Определите индекс массива validpos и инициализируйте его так, чтобы он указывал на первую позицию в hufflist массива, то есть validpos ← 0. В процессе построения дерева Хаффмана каждый раз, когда узел добавляется к дереву Хаффмана, массив уменьшается на один узел, и validpos используется для указания на каждый узел, используемый для построения дерева. Инициализация validpos начинается с позиции 0, и первые два узла массива объединяются, чтобы сохранить полученный промежуточный узел в позицию 1, то есть позицию validpos + 1. В это время узел в позиции 0 становится недопустимым узлом. Затем увеличьте validpos на 1, указывая на только что созданный промежуточный узел.

Поскольку значение вероятности этого узла является суммой двух исходных узлов, его значение вероятности может быть больше, чем значение вероятности последующих узлов. Положение промежуточного узла может потребовать корректировки: начните с позиции validpos + 1 найти первый для узлов с большими значениями вероятности, затем скорректировать положения элементов. Продолжайте повторять этот процесс, пока validpos не укажет на последний элемент массива.

Конкретные шаги заключаются в следующем:

1. validpos ← 0, отсортировать список списков массивов от маленького к большему.

2. И объедините два узла в позиции validpos и validpos + 1 hufflist с lft и rght:

Сначала создайте новый объект r типа HuffmanPair, установите позицию как содержимое левого дочернего узла r и rght как содержимое правого дочернего узла r;

Затем частота freq r устанавливается равной сумме freq lft и rght, а символ сигнала c устанавливается на недопустимый символ сигнала “□”

Наконец, validpos ← validpos + 1 и сбрасывает элемент в позиции validpos hufflist на r;

3. Отрегулируйте положение элемента в допустимой позиции hufflist:

Найдите позицию idx первого элемента не ниже hufflist [validpos] в hufflist;

Переместите элемент в позиции validpos ~ idx-2 в hufflist вправо на одну позицию, а затем назначьте элемент в позиции idx-1 массива в позицию validpos;

4. Верните 2, чтобы продолжить итерацию, пока validpos не станет равным n-1.

В качестве примера возьмем hufflist:

1. Отсортируйте элементы в hufflist от маленького к большему и установите validpos ← 0:

Позиция тени допустима;

2. Объедините два узла в позиции validpos = 0 и позиции validpos + 1 = 1, чтобы получить промежуточный узел со значением вероятности 0,01 + 0,1 = 0,11. После изменения положения результат будет следующим:

validpos ← validpos + 1 = 1, фактически, элемент в позиции 0 в настоящее время недействителен, что обозначено светлым цветом;

3. Объедините два узла в validpos = 1 и validpos + 1 = 2, чтобы получить промежуточный узел со значением вероятности 0,11 + 0,15 = 0,26. После повторной корректировки положения результат будет следующим:

validpos ← validpos + 1 = 2, можно обнаружить, что положение промежуточного узла с вероятностью 0,26, полученной на этом этапе, было скорректировано с положения 2 на положение 6;

4. Объедините два узла в validpos = 2 и validpos + 1 = 3, чтобы получить промежуточный узел со значением вероятности 0,17 + 0,18 = 0,35. После повторной корректировки положения результат будет следующим:

validpos ← validpos + 1 = 3, можно обнаружить, что положение промежуточного узла с вероятностью 0,35, полученное на этом этапе, было скорректировано с положения 3 на положение 6;

5. Объедините два узла с validpos = 3 и validpos + 1 = 4, чтобы получить промежуточный узел со значением вероятности 0,19 + 0,2 = 0,39. После повторной корректировки положения результат будет следующим:

validpos ← validpos + 1 = 4, можно обнаружить, что положение промежуточного узла со значением вероятности 0,39, полученным на этом этапе, было скорректировано с положения 4 на положение 6;

6. Объедините два узла с validpos = 4 и validpos + 1 = 5, чтобы получить промежуточный узел со значением вероятности 0,26 + 0,35 = 0,61. После повторной настройки положения результат будет следующим:

validpos ← validpos + 1 = 5, можно обнаружить, что положение промежуточного узла с вероятностью 0,61, полученное на этом шаге, корректируется с положения 5 на положение 6;

7. Последний раз, когда узлы объединяются, окончательный hufflist:

На этом этапе validpos равно n-1, и итерация заканчивается.

Назначьте последний элемент массива hufflist, а именно hufflist [n-1], корневому узлу двоичного дерева, чтобы завершить построение дерева Хаффмана.

Благодаря приведенному выше подробному обсуждению процесса создания дерева Хаффмана структура данных дерева Хаффмана может быть спроектирована как:

package Tree;

import Element.ElemItem;

/**
  *
  *
дерево Хаффмана, основная переменная-член – корневой узел дерева,
* Основными функциями-членами являются построение и печать дерева.
  * HuffmanTree.java
  */

public class HuffmanTree {

     //Переменная частного члена
     //Корневой узел дерева
     private LinkBinTreeNode root;

     //Конструктор без параметров
     public HuffmanTree(){

         root = null;

     }

     //Параметризованный конструктор
     public HuffmanTree(LinkBinTreeNode r){

         root = r;

     }

     //Постройте дерево Хаффмана, введите параметр в виде связанного списка
     //Элемент связанного списка – HuffmanPair
     public void buildTree(LinkBinTreeNode hufflist[]){

         //Сначала отсортируйте элементы hufflist
         //Длина массива
         int n = hufflist.length;

         //Положение первого действительного узла в массиве
         int validpos = 0;

         //Простая сортировка выбора
         for(int i = 0; i < n; i++){

             for(int j = i + 1; j < n; j++){

                 //Если i-я частота больше j-й частоты, замените
                 if(((HuffmanPair)(

                         hufflist[i].getElem().getElem()

                         )).compareTo(

                     (HuffmanPair)(

                         hufflist[j].getElem().getElem()

                         )) == 1){

                     LinkBinTreeNode t = hufflist[i];

                     hufflist[i] = hufflist[j];

                     hufflist[j] = t;

                 }

             }

         }//Сортировка завершена//Начать строить
         while(validpos != n -1){

             //Новый узел используется для представления корневого узла двух поддеревьев.
             LinkBinTreeNode r

                 = new LinkBinTreeNode();

             //Установите левое и правое поддеревья корневого узла r
             r.setLeft(hufflist[validpos]);

             r.setRight(hufflist[validpos + 1]);

             //Добавьте частоты левого и правого дочерних узлов
             double _f =

                 ((HuffmanPair)(

                     hufflist[validpos].getElem().getElem()

                     )).getFreq()

               + ((HuffmanPair)(

                       hufflist[validpos+1].getElem().getElem()

                       )).getFreq();

             //Задайте частоту узла, и символ узла представлен “□”
             r.setElem(new ElemItem<HuffmanPair>(

                     new HuffmanPair(“□”, _f)));

             //Эффективная позиция перемещается назад
             validpos++;

             //Сбросьте позицию validpos на вновь созданный узел
             hufflist[validpos] = r;

             //Отрегулируйте положение узла validpos,
             //Поскольку значение частоты не обязательно является наименьшим
             int idx;

             //huffmanPair at validpos
             HuffmanPair tt1 =

                 (HuffmanPair)(

                     hufflist[validpos].getElem().getElem());

             //Найдите позицию idx первого узла с большей частотой, чем tt1
             for(idx = validpos + 1; idx < n; idx++){

                 HuffmanPair tt2 =

                 (HuffmanPair)(

                     hufflist[idx].getElem().getElem());

                 //Найдите первый больше idx
                 if(tt1.compareTo(tt2) <= 0){

                     break;

                 }

             }

             //Кэшировать узел validpos,
             //И переместите validpos ～ idx- 1huffmanPair вперед по очереди
             LinkBinTreeNode t = hufflist[validpos];

             for(int i = validpos; i < idx – 1; i++){

                 hufflist[i] = hufflist[i + 1];

             }

             //Поместите t в нужное место
             hufflist[idx – 1] = t;

         }

         //Последний корневой узел – это последняя пара huffman в hufflist.
         root = hufflist[n – 1];

     }

     //Выведите узел n на высоте h
     protected void printnode(LinkBinTreeNode n, int h){

         //Высота табуляции h
         for(int i = 0; i < h; i++){

             System.out.print(“t”);

         }

         //Получите форму одинарной точности значения частоты узла
         double _f = (

             (HuffmanPair)(

                 n.getElem().getElem())).getFreq();

         float f = (float)(_f);

         //Строка узла, различающая листовые узлы и промежуточные узлы.
         String c;

         //Для листовых узлов c – строковое значение узла
         if(n.isLeaf()){

             c = ((HuffmanPair)(

                 n.getElem().getElem())).getChar();

         }

         //Для промежуточных узлов c пусто
         else{

             c = “□”;

         }

         //Узел печати
         System.out.println(“–” + c + ” ” + f);

     }

     //Выведите дерево Хаффмана с узлом r в качестве корневого узла,
     //Высота r равна h, вызовите функцию печати узла,
     //Эта функция рекурсивная
     public void ShowHT(LinkBinTreeNode r, int h){

         //Корень пуст, возвращаемся напрямую
         if(r == null){

             return;

         }

         //Рекурсивный вызов для отображения дерева с правым узлом r в качестве корневого узла
         //Высота h + 1
         ShowHT(r.getRight(), h + 1);

         //Распечатать узел r
         printnode(r, h);

         //Рекурсивный вызов для отображения дерева с левым узлом r в качестве корневого узла
         //Высота h + 1
         ShowHT(r.getLeft(), h + 1);

     }

     //Распечатайте дерево Хаффмана, то есть распечатайте дерево с корнем в качестве корневого узла
     //Начальная высота 0
     public void printTree(){

         ShowHT(root, 0);

     }

     //Тестировать предварительный заказ, средний заказ, пост-заказ и обход последовательности слоев
     public void order_visit(){

         LinkBinTree lbt = new LinkBinTree(root);

         //Два предварительных теста
System.out.println (” nРекурсивный алгоритм для достижения обхода предварительного заказа:”);

         lbt.rec_preorder(lbt.getRoot());

System.out.println (” nИтеративный алгоритм для достижения обхода предварительного заказа:”);

         lbt.itr_preorder(lbt.getRoot());

         //Два промежуточных теста
System.out.println (” nРекурсивный алгоритм для достижения обхода среднего порядка:”);

         lbt.rec_inorder(lbt.getRoot());

System.out.println (” nИтеративный алгоритм для достижения обхода по порядку:”);

         lbt.itr_inorder(lbt.getRoot());

         //Два последующих теста
System.out.println (” nРекурсивный алгоритм реализует обход после заказа:”);

         lbt.rec_postorder(lbt.getRoot());

System.out.println (” nИтеративный алгоритм реализует обход пост-заказа:”);

         lbt.itr_postoder(lbt.getRoot());

         //Последовательный тест
System.out.println (” nИтеративный алгоритм для достижения обхода последовательности слоев:”);

         lbt.layer_order(lbt.getRoot());

     }

}

В реализованной структуре данных дерева Хаффмана частная переменная-член является корнем корневого узла дерева Хаффмана типа узла двоичного дерева. Функция buildTree реализует создание дерева Хаффмана, а параметр функции представляет собой массив типа LinkBinTreeNode. При построении дерева сначала отсортируйте все узлы в массиве по значению частоты символа сигнала от маленького к большому. Здесь используется простая сортировка с выбором. Затем итеративно выполните комбинацию узлов и настройку положения.

Кроме того, здесь мы также используем различные способы отображения информации о каждом узле в дереве Хаффмана. В предыдущей главе мы обсудили метод отображения обобщенного дерева после поворота на 90 градусов, а также обсудили метод отображения структуры кучи после поворота на 90 градусов. Здесь мы также используем метод отображения поворота на 90 градусов для Дерево Хаффмана.

Функция ShowHT отображает информацию об узле r на высоте h. Эта функция является рекурсивной функцией. Если узел r пуст, вернитесь; в противном случае, если правый дочерний узел r не пуст, сначала рекурсивно распечатайте правый дочерний узел r на высоте h + 1; затем распечатайте узел r на высоте h и вызовите функцию printnode; наконец , если левый дочерний узел r не пуст, рекурсивно вывести левый дочерний узел r на высоте h + 1.

Мы также упоминали ранее, что дерево Хаффмана является специальным двоичным деревом, поэтому все алгоритмы обхода двоичного дерева также применимы к дереву Хаффмана. Здесь мы также выполняем обход порядка предварительного, среднего, пост-порядка и порядка слоев в дереве Хаффмана и напрямую вызываем соответствующую функцию класса двоичного дерева.

Ниже приведен тестовый образец программы для дерева Хаффмана:

/**
  *
  *
* пример программы проверки дерева Хаффмана,
  * ExampleHuffmanTree.java
  */

public class ExampleHuffmanTree {

     public static void main(String args[]){

         //Строка, представление массива, длина 7
         String c[] = new String[7];

         //Установите значение строки
         c[0] = “a1”; c[1] = “a2”;

         c[2] = “a3”; c[3] = “a4”;

         c[4] = “a5”; c[5] = “a6”;

         c[6] = “a7”;

         //Частота, соответствующая строке, представленной массивом
         double frq[] = {0.2, 0.19,

                     0.18, 0.17,

                     0.15, 0.1,

                     0.01};

         //Массив дерева узлов, используемый для построения дерева Хаффмана
         LinkBinTreeNode n[] = new LinkBinTreeNode[7];

         //Присвоение номеров узлов
         for(int i= 0; i < 7; i++){

             n[i] = new LinkBinTreeNode(

                     new ElemItem<HuffmanPair>(

                             new HuffmanPair(c[i], frq[i])),

                     null, null);

         }

         //Создать объект дерева
         HuffmanTree ht = new HuffmanTree();

         //Делать вклад
         ht.buildTree(n);

         //Распечатать дерево
         ht.printTree();

         //Различные алгоритмы обхода бинарных деревьев
         ht.order_visit();

     }

}

Сигнал каждого узла созданного дерева Хаффмана соответствует той же частоте, что и в приведенной выше подпрограмме:

P(a1)=0.2，P(a2)=0.19，P(a3)=0.18，

P(a4)=0.17，P(a5)=0.15，P(a6)=0.1，P(a7)=0.01。

Были протестированы создание Хаффмана, печать с поворотом на 90 градусов и различные алгоритмы обхода. Результаты были следующими:

        –a3 0.18

            –□ 0.35

                –a4 0.17

        –□ 0.61

                –a5 0.15

            –□ 0.26

                    –a6 0.1

                –□ 0.11

                    –a7 0.01

    –□ 1.0

            –a1 0.2

        –□ 0.39

            –a2 0.19

Рекурсивный алгоритм реализует обход предварительного порядка:

–□ 1.0→–□ 0.39→–a2 0.19→–a1 0.2→–□ 0.61→–□ 0.26→–□ 0.11→–a7 0.01→–a6 0.1→–a5 0.15→–□ 0.35→–a4 0.17→–a3 0.18→

Итерационный алгоритм для достижения обхода предзаказа:

–□ 1.0→–□ 0.39→–a2 0.19→–a1 0.2→–□ 0.61→–□ 0.26→–□ 0.11→–a7 0.01→–a6 0.1→–a5 0.15→–□ 0.35→–a4 0.17→–a3 0.18→

Рекурсивный алгоритм для выполнения обхода по порядку:

–a2 0.19→–□ 0.39→–a1 0.2→–□ 1.0→–a7 0.01→–□ 0.11→–a6 0.1→–□ 0.26→–a5 0.15→–□ 0.61→–a4 0.17→–□ 0.35→–a3 0.18→

Итерационный алгоритм для достижения обхода по порядку:

–a2 0.19→–□ 0.39→–a1 0.2→–□ 1.0→–a7 0.01→–□ 0.11→–a6 0.1→–□ 0.26→–a5 0.15→–□ 0.61→–a4 0.17→–□ 0.35→–a3 0.18→

Рекурсивный алгоритм реализует обход постзаказа:

–a2 0.19→–a1 0.2→–□ 0.39→–a7 0.01→–a6 0.1→–□ 0.11→–a5 0.15→–□ 0.26→–a4 0.17→–a3 0.18→–□ 0.35→–□ 0.61→–□ 1.0→

Итерационный алгоритм реализует обход постзаказа:

–a2 0.19→–a1 0.2→–□ 0.39→–a7 0.01→–a6 0.1→–□ 0.11→–a5 0.15→–□ 0.26→–a4 0.17→–a3 0.18→–□ 0.35→–□ 0.61→–□ 1.0→

Итерационный алгоритм обхода последовательности слоев:

–□ 1.0→–□ 0.39→–□ 0.61→–a2 0.19→–a1 0.2→–□ 0.26→–□ 0.35→–□ 0.11→–a5 0.15→–a4 0.17→–a3 0.18→–a7 0.01→–a6 0.1→

Дерево Хаффмана в природе

Метод определения числа Хаффмана является примером жадного алгоритма.Для получения подробной информации о жадном алгоритме, пожалуйста, обратитесь к соответствующим результатам поиска в Интернете. Благодаря подробному обсуждению, приведенному выше, мы можем обнаружить, что на каждом этапе комбинации узлов два узла – это два с наименьшим значением вероятности. Но может ли такой жадный процесс гарантировать желаемый результат, то есть минимальную длину взвешенного пути? Докажем, что дерево Хаффмана действительно дает наилучшее расположение информационных символов.

Лемма 1 Дерево Хаффмана, содержащее по крайней мере два узла, будет хранить два сигнальных символа с наименьшей частотой сигнального символа как одноуровневые узлы, а количество слоев не меньше любого другого листового узла в дереве.

Доказательство: смысл леммы состоит в том, что сигнальный символ с меньшей частотой будет располагаться в позиции листового узла с большим количеством слоев, который легче найти интуитивно на основе закона.

Докажите от противного:

Два информационных символа с наименьшим значением частоты – это x1 и x2. Так как два узла, выбранные на первом шаге при построении дерева Хаффмана, являются ими, они должны быть парой узлов-братьев. Предположим, что x1 и x2 не являются узлами с наибольшим числом слоев в дереве Хаффмана, то есть существует x0, количество слоев которого больше, чем x1 и x2, как показано на рисунке. В это время значение вероятности родительского узла F для x1 и x2 должно быть больше, чем x0, иначе при построении дерева F вместо x0 будет выбран в качестве дочернего узла F2. Однако при условии, что «x1 и x2 – два информационных символа с наименьшим значением вероятности», такая ситуация не может произойти.

Рисунок Существует противоречивое дерево Хаффмана, поддерево которого представлено треугольником

Свойство 1 Для данного набора информационных символов дерево Хаффмана реализует «минимально взвешенный путь».

Доказательство. Докажите индуктивным способом количество информационных символов n.

Когда n = 2, дерево Хаффмана должно иметь наименьший взвешенный путь, потому что в это время существует только два дерева, а взвешенные пути двух листовых узлов одинаковы;

Предположим, что дерево Хаффмана с n <k листовыми узлами имеет наименьший взвешенный путь;

Когда n = k, установите w1 <… <wk, где w1, …, wk представляют правую часть информационного символа. Пусть F будет родительским узлом двух информационных символов w1 и w2. Согласно лемме, они уже являются узлами с наибольшим числом слоев в дереве T, и нет узла с большим числом слоев и большими весами, который мог бы заменить их, чтобы уменьшить длину пути. Помните, что дерево Хаффмана T ‘точно такое же, как и T, за исключением того, что узел F (и поддерево, образованное его дочерними узлами) заменяется листовым узлом F’, а его вес равен w1 + w2. Согласно индуктивной гипотезе, T ‘имеет наименьший взвешенный путь. Наконец, замените F ‘дочерними узлами w1 и w2, и T, эквивалентный T, также должен иметь наименее взвешенный путь.

Кодирование Хаффмана и его использование

Последним шагом при введении кодирования Хаффмана в начале этого раздела является присвоение значений с помощью элементов двоичного кода (0-1) для формирования кодового слова Хаффмана. Эта форма кодового слова Хаффмана 0-1 фактически является окончательной формой кодирования Хаффмана. .

Как только дерево Хаффмана построено, мы можем закодировать каждый информационный символ. Начиная с корневого узла, пометьте каждое ребро двоичного дерева цифрами 0 и 1 соответственно. «0» соответствует ребру, соединяющему левый дочерний узел, а «1» – ребру, соединяющему правый дочерний узел. На рисунке показан этот процесс. Код Хаффмана информационного символа состоит из метки каждого ребра на пути от корневого узла до листового узла информационного символа. Результаты кодирования Хаффмана каждого информационного символа на рисунке следующие:

Информационный символ	частота	кодирование	Длина двора
a1	0.2	01	2
a2	0.19	00	2
a3	0.18	111	3
a4	0.17	110	3
a5	0.15	101	3
a6	0.1	1001	4
a7	0.01	1000	4

Рисунок соответствующийФигураРезультат кодирования Хаффмана

Для данной информационной строки может быть выполнено кодирование Хаффмана в соответствии с результатом кодирования для получения строки 0-1 бит. Просто замените каждый символ сообщения в строке сообщения соответствующим кодовым словом Хаффмана. Например, учитывая информационную строку «a1a1a4a1a2a5», она может быть представлена как «01011100100101».

При выполнении обратного кодирования (декодирования) результата кодирования оценка производится побитно слева направо, что может быть достигнуто путем использования процесса, обратного процессу генерации кодового слова для дерева Хаффмана. Начиная с корневого узла дерева, кодовое слово информационной строки подвергается обратному кодированию. В зависимости от того, равно ли значение каждого бита 0 или 1, определяется, выбирает ли дерево Хаффмана левый узел или узел в каждой ветви – до тех пор, пока не будет достигнут листовой узел, информационный символ, содержащийся в этом листовом узле, является результатом расшифровка. Согласно этому способу кодовое слово данного информационного символа может быть декодировано.

Декодирование кодового слова «01011100100101», начиная с корневого узла, поскольку первый бит равен 0, выбирается левая ветвь. Следующий бит равен 1, поэтому выберите правую ветвь и достигните листового узла, соответствующий информационный символ – a1, то есть переведенный результат – a1. Затем снова вернитесь к корневому узлу, начиная с корневого узла, начиная с третьего бита кодового слова, равного 0, выберите левый числитель, затем выберите правую ветвь и по-прежнему переводите a1. Затем начните с корневого узла, бит равен 1, выберите правую ветвь, а затем выберите правую ветвь и левую ветвь, чтобы достичь конечного узла, и результат перевода будет a4. Точно так же после завершения всего декодирования вы можете обнаружить, что конечный результат – «a1a1a4a1a2a5».

Фактически кодирование Хаффмана – это префиксный код. Если какое-либо кодовое слово в кодовом слове не является префиксом другого кодового слова, группа кодовых символов называется префиксом. Этот вид префикса гарантирует, что не будет нескольких возможностей декодирования информационной строки. Другими словами, при декодировании, когда мы достигаем последнего бита определенного кода, мы можем судить об информационном символе, который он представляет. Поскольку префикс любого кодового слова соответствует узлу ветвления, и каждое кодовое слово имеет соответствующий информационный символ, кодовое слово, полученное с помощью кодирования Хаффмана, соответствует префиксу.

Перепечатано по адресу: https://www.cnblogs.com/ajian005/archive/2012/11/08/2841161.html

Источник

Всем привет!

Дано двоичное дерево поиска. Ключи – целые числа. Нужно найти самый длинный путь (максимальной длины) между двумя любыми вершинами дерева с разным числом потомков.

Для начала я бы хотел уточнить:
1. путь может проходить как угодно по дереву, т е, например из левого дерева подниматься к корню и затем уходить в правое поддерево? Т е путю необязательно двигаться по связям вершин дерева?
2. вроде гарантируется, что одной из такой вершин будет лист, т к появление листа гарантировано увеличивает протяженность пути на +1. Два листа быть не может, т к у них будет равное число потомков = 0.
3. число потомков ведь может быть 0, когда берется лист
4. вроде не гарантируется, что эти две вершины будут лежать по разные стороны от корня исходного дерева? Например, ДДП, которое выродилось в ЛОС, там все элементы принадлежат одному из поддеревьев. Кстати, в случае ЛОС-ДДП максимальный путь будет проложен от корня до листа.

Какие мысли есть: найти кол-во потомков для КАЖДОГО узла исходного ДДП (это я знаю, как сделать). А даст ли это что-нибудь?! Наверное, придется еще получить номер уровня для каждого узла дерева, не знаю)

Может существует какое-то простое решение (типа одной рекурсивной функцией), решающее такую проблему??

P.S. возможно, что здесь нужно каким-то боком задействовать дин.прогр. + может быть, преобразовать структуру в граф (хотя дерево и так есть разновидность графа в любом случае)

Источник

Understanding the recursion

Counting Nodes

Counting edges

Translating the definition into maths

Тема: Деревья

Математические свойства бинарных деревьев

Вам также может понравиться

Посылки без отслеживания как найти посылку

Как найти вместимость баллона

Шумит кулер в компьютере как исправить чем смазать

Добавить комментарий Отменить ответ