Нам дан рисунок http://bit.ly/2DrKmdp на котором изображен жук, который ползет вдоль ребер прямоугольного параллелепипеда AM, MB, BC, CD. Нужно найти длину пути жука.
Давайте составим план действий для решения задачи
- первым действием посмотрим на рисунок и проследим весь путь жука по ребрам прямоугольного параллелепипеда;
- длины ребер параллелепипеда над даны на рисунке, выпишем их длину;
- для того, чтобы найти весь путь жука нужно сложить длины всех ребер, по которым прополз жук;
- запишем ответ задачи.
Найдем длину пути, который прополз жук по ребрам прямоугольного параллелепипеда
Давайте посмотрим на рисунок и проследим весь путь жука.
Итак, жук ползет по ребрам AM и MB длины которых обозначены на рисунке и соответственно равны 4 дм и 2 дм, а затем по ребрам BC и CD длины которых нам нужна найти пользуясь свойством прямоугольного параллелепипеда.
Так как в прямоугольном параллелепипеде противоположные грани параллельны и равны, делаем вывод, что СD = NB = AM = 4 дм.
А BC = 3 дм по тому же свойству.
Длины всех граней прямоугольного параллелепипеда по которому прополз жук известны и равны соответственно AM = 4 дм, MB = 2 дм, BC = 3 дм и CD = 4 дм.
Теперь найдем длину всего пути который проделал жук по граням прямоугольного параллелепипеда сложив длины всех сторон, по которыми он прополз.
То есть,
AM + MB + BC + CD = 4 дм + 2 дм + 3 дм + 4 дм = 13 дм.
Значит жук прополз пути в 13 дм.
Теперь можем перейти к записи ответа.
Ответ: жук прополз по ребрам прямоугольного параллелепипеда 13 дм.
а) Для начала введём обозначения для вершин параллелепипеда (см. рис. 2) и его граней: назовём грань ABCD нижней, EFGH — верхней, ABFE — передней, CDHG — задней, BCGF — правой и, соответственно, ADHE — левой.

Мы будем активно пользоваться соображениями симметрии. Например, раз мы минимизируем расстояние, проползаемое божьей коровкой, то можно считать, что она всё время будет находиться по одну сторону от сечения ACGE — ведь если бы божья коровка несколько раз пересекала границу этого сечения, то оптимальнее ей было бы ползти по его границе между точками пересечения её пути с этим сечением. Будем считать, что она ползёт по «ближней» к нам части параллелепипеда из двух, на которые сечение его разбивает, то есть содержащей точки B и F.
Далее, ясно, что для каждой грани, по которой предстоит ползти божьей коровке, её путь по этой грани должен представлять собой отрезок: ведь это — кратчайшее расстояние между двумя точками на плоскости и, что немаловажно, любые две точки каждой из наших граней мы можем соединить отрезком, целиком лежащим в той же грани (тут нам помогает выпуклость каждой из граней параллелепипеда).
Теперь видно, что у нас есть три потенциально быстрых способа передвижения: 1) по передней грани и затем по правой; 2) по передней грани и затем по верхней; 3) по нижней грани и потом по какой-то из боковых граней. Третий способ, на самом деле, равносилен второму, и вот почему: мы можем поменять местами начальную и конечную точки пути божьей коровки (или, что то же самое, произвести отражение нашего параллелепипеда относительно его центра), и тогда путь, начинающийся с нижней грани, перейдёт в путь, заканчивающийся на верхней грани. Так что достаточно рассмотреть два первых способа: с передней на правую и с передней на верхнюю грань.
Как же понять для каждого из способов, какой путь по соответствующим граням самый оптимальный — то есть в каком месте божьей коровке надо пересечь ребро между гранями (BF в первом случае и EF во втором)? Для этого рассмотрим развёртку параллелепипеда (точнее, его части). Например, если мы договорились, что рассматриваем путь божьей коровки только по передней и правой граням, то можем считать, что между гранями ABFE и BCGF не прямой, а развёрнутый угол, то есть они лежат в одной и той же плоскости. Можем, действительно, разрезать эти грани и уложить их в одну плоскость — и если божья коровка не заметит «неправильного» угла в тот короткий миг, когда будет переползать с одной грани на другую, то в остальном ей совершенно всё равно, под каким углом расположены грани; на длину её пути он никак не повлияет.
Начнём с первого способа: передняя и правая грани. Расположив эти грани в одной плоскости, мы получим квадрат ACGE со стороной 20 см, причём начало и конец маршрута (точки A и G) расположатся в противоположных его концах. Ползти божьей коровке, конечно, нужно прямо по диагонали квадрата (таким образом, ребро BF она пересечёт в его середине), и пройденный путь составит, согласно теореме Пифагора, 20√2 ≈ 28,28 см.

Теперь второй способ. «Распрямив» переднюю и верхнюю грани, мы получим прямоугольник ABGH со сторонами 10 и 30 см. Начало и конец маршрута снова оказываются его противоположными вершинами, и кратчайшим путём снова будет диагональ прямоугольника. Но здесь она равна 10√10 ≈ 31,62 см — гораздо больше. Таким образом, первый способ оптимален, и кратчайшим будет путь, найденный первым способом: из точки A — в середину ребра BF, а оттуда — в точку G.
б) Из предыдущего пункта ясно, что во все точки боковых граней божья коровка может добраться, проползя не больше 20√2 ≈ 28,28 см. До всех точек нижней грани ей ползти еще ближе. Так что если и есть где-то для божьей коровки более далёкие точки, чем G, то они находятся на верхней грани.
Для их поиска введём систему координат на верхней грани: за начало координат возьмём точку E, осью абсцисс сделаем луч EF, а осью ординат — луч EH. Пусть искомая самая далёкая точка W имеет координаты (x, y). По-прежнему будем считать, что точка находится на «ближней» к нам половинке параллелепипеда, на которые его делит плоскость ACGE; это означает, что 0 ≤ y ≤ x ≤ 10.
Что вообще даёт нам надежду, что есть более далёкие точки, чем G? Тот факт, что путь через верхнюю грань до G оказался гораздо длиннее пути через правую грань. Это означает, что если мы заберёмся по верхней грани немного левее точки G (но не пересекая диагональ EG, чтобы не появлялись альтернативные короткие пути через левую грань) — в направлении точки H, — то путь через правую грань ещё увеличится, в то время как путь через верхнюю грань уменьшится не столь сильно, чтобы сравняться с «правым» путём.
Перейдём к расчётам. Путь через верхнюю грань из точки A в точку W(x, y) по-прежнему будет просто диагональю в прямоугольнике; его стороны составят x и (20 + y) — таким образом, квадрат диагонали будет равен S1 = x2 + y2 + 40y + 400.
Путь же через правую грань теперь будет проходить уже по трём граням — передней, правой и верхней; но мы можем точно так же расположить их все в одной плоскости и посмотреть на диагональ получившегося прямоугольника. Его стороны составят (10 + y) и (30 – x), и квадрат диагонали будет равен S2 = x2 + y2 – 60x + 20y + 1000.
Найдём, при каких условиях на x и y первый путь короче:
S1 < S2,
x2 + y2 + 40y + 400 < x2 + y2 – 60x + 20y + 1000,
60x + 20y < 600,
y < 30 – 3x.
Таким образом, разные способы добраться до точки W будут равны, если эта точка лежит на некотором отрезке на верхней грани (ведь y = 30 – 3x — это линейная функция). Максимум расстояния от божьей коровки (то есть от точки A) будет достигаться как раз для одной из точек на этом отрезке: ведь если в некоторой точке S1 < S2, то мы можем ещё немного отодвинуться от точки A в направлении, в котором кратчайший путь, построенный первым способом, движется от A к W, и S2 при этом уменьшится не слишком сильно.

Подставив y = 30 – 3x, например, в выражение для S1 (поскольку при таком y S1= S2, можно выбрать более простое из выражений, получим S1 = 10x2 – 300x + 2500. Это парабола с ветвями, направленными вверх, и абсцисса её вершины равна 15. Поскольку у нас x не превышает 10 и нас интересует как можно большее значение расстояния, то нам нужно взять как можно больший x; однако не забудем, что мы предполагаем, что абсцисса больше ординаты, так что подойдут только те точки, в которых x ≤ y, то есть 30 – 3x ≤ x, или x ≥ 7,5. Значит, оптимальной будет как раз точка с абсциссой и ординатой, равными 7,5 см; она лежит на диагонали верхней грани EG и делит её в отношении 3:1, считая от точки E. Расстояние до неё составит √(812,5) ≈ 28,50 см — на два с лишним миллиметра больше, чем расстояние до точки G.
в) Здесь заметим для начала, что достаточно рассмотреть пары точек на верхней и нижней гранях — ясно, что для любой другой пары точек можно перенести одну из них на квадратную грань так, что расстояние от неё до второй точки увеличится. Кроме того, из соображений симметрии можно считать, что точка в нижней грани лежит в треугольнике AMH (он выделен жёлтым на рис. 5). Точки верхней грани, наиболее далёкие от него, лежат в жёлтом квадратике: легко понять, что для любой другой точки верхней грани можно выбрать точку в этом квадратике, более удалённую от любой точки в треугольнике AMH. (А вот можно ли указать в верхней грани треугольник размером с AMH, в котором точно лежат самые удалённые точки, уже не столь ясно.)

Есть два принципиально разных способа добраться из нижней грани на верхнюю: посетив при этом одну боковую грань или две боковые. Легко понять, что посещение трёх и больше граней никакой пользы не принесёт — такие пути легко можно укоротить. Поймём сначала, для каких пар точек на верхней и нижней гранях кратчайший из путей через одну боковую грань (таких путей, очевидно, как и боковых граней, четыре штуки) максимален.
Как и в предыдущем пункте, введём системы координат — теперь и в нижней, и в верхней гранях. В нижней осями абсцисс и ординат соответственно будут лучи AB и AG, в верхней — лучи FH и FD. Пусть наши точки суть V (a, b) и W (c, d); тогда уже оговоренные условия означают, что 0 ≤ b ≤ a ≤ 5 и 0 ≤ c, d ≤ 5.
Покажем, что для любых таких точек V, W найдётся путь между ними по поверхности параллелепипеда, длина которого не превышает 30 см. Оказывается, достаточно рассмотреть лишь пути, которые проходят не более чем по одной боковой грани, то есть идут сначала по нижней грани, затем по какой-то из четырёх боковых и сразу с неё попадают на верхнюю грань.
Итак, посмотрим, при каких a, b, c, d кратчайший путь между V и W будет длиннее всего. Для этого нарисуем развёртку параллелепипеда во все четыре стороны (верхнюю грань оставим на месте) и по теореме Пифагора выпишем квадраты длин путей по всем четырём боковым сторонам (их номера проставлены на рис. 6):
S1 = (10 – a – c)2 + (30 + d – b)2,
S2 = (10 – a – c)2 + (30 + b – d)2,
S3 = (30 + a – c)2 + (10 – b – d)2,
S4 = (30 – a + c)2 + (10 – b – d)2.

![]()
Всё не так страшно, как может показаться. Посмотрим сначала на S1 и S2: первые слагаемые у них одинаковы, а вторые различаются тем сильнее, чем больше отличаются b и d, причём одно из них уменьшается, а другое увеличивается. Но мы хотим найти значения параметров, при которых все расстояния будут достаточно велики. Поэтому если числа b и d различны, их можно заменить на полусумму (b + d)/2; при этом минимальное из чисел S1 и S2 возрастёт, а S3 и S4 останутся прежними. Таким образом, можно считать, что b = d, и при этом S1 = S2.
Аналогично, рассмотрев суммы S3 и S4, заметим, что можно считать равными числа a и c (это соответствует тому, что точки V и W лежат на диагоналях AC и EG своих граней), а значит, S3 = S4.
Наконец, сравним первый и третий пути — например, посмотрим, при каких значениях параметров a и c первый путь короче. Не забываем, что a и c не превышают 5 см:
S1 < S3,
(10 – 2a)2 + 302 < 302 + (10 – 2b)2,
10 – 2a < 10 – 2b,
b < a.
Таким образом, одинаково далеко добираться от V к W по первому и третьему пути (а значит, и по всем четырём путям сразу!), если a = b, то есть точки V и W симметричны друг другу относительно центра параллелепипеда.
Дело за малым — найти длину всех этих путей. Её квадрат равен
S1 = (10 – 2a)2 + 302 = 4a2 – 40a + 1000;
это — парабола с ветвями, направленными вверх, и вершиной в точке a = 5. Таким образом, чем ближе наши точки V, W к противоположным вершинам параллелепипеда (например, к A и F), тем расстояние между ними больше.
Но мы знаем, что есть путь для божьей коровки A до F даже короче, чем путь между центрами верхней и нижней граней (28,50 см против 30 см)! Просто он проходит сразу через две боковые грани, а мы такие пути пока не рассмотрели. Значит, подобный же путь будет оптимальным и для точек на наших диагоналях граней AE и CF, достаточно близких к A и F. Найдём теперь, когда же пути по одной боковой и по двум боковым граням оказываются одинаково плохими (или одинаково хорошими, что то же самое).
Вообще говоря, для любых двух точек V и W на нижней и верхней гранях число путей, проходящих по двум боковым граням, снова равно четырём — именно столько есть пар соседних боковых граней у параллелепипеда. Предоставим читателю самому проверить, что и для таких путей самыми неприятными оказываются пары точек на квадратных гранях, симметричные друг другу относительно центра параллелепипеда — то есть ситуация ровно та же, что и с путями по одной боковой стороне.
Ну а путь по двум боковым сторонам для точек V и W на диагоналях, то есть с координатами (а, а) и (а, а) — каждая в своей системе координат, — найти после проделанной работы нам совсем легко, см. рис. 7.

Квадрат искомого расстояния будет равен
S5 = (20 – 2a)2 + (20 + 2a)2 = 8a2 + 800.
Проверяем, для каких значений а из отрезка [0; 5] этот путь будет короче пути по одной боковой стороне:
S5 < S1,
8a2 + 800 < 4a2 – 40a + 1000,
a2 + 10a – 50 < 0,
a < 5√3 – 5 ≈ 3,66.
Всё согласуется с нашими представлениями: при маленьких значениях a, то есть пока точки находятся возле вершин, кратчайшим является путь через две боковые грани, похожий на решение пункта б). А для точек, близких к центрам граней, оптимальнее оказывается посещать лишь одну боковую грань.
Итак, искомые точки V и W находятся на квадратных гранях, симметричны друг другу относительно центра параллелепипеда и удалены от каждой из ближайших сторон граней на a = 5(√3 – 1) ≈ 3,66 см. Квадрат кратчайшего пути между ними равен 8(5√3 – 5)2 + 800 = 400(4 – √3), а сам путь составляет примерно 30,12 см — лишь на миллиметр с небольшим длиннее пути между центрами квадратных граней. Впрочем, сам факт, что точки на большем расстоянии, чем 30 см, нашлись, представляется нам достаточно удивительным, чтобы оправдать существование задачи.
22 января 2014
Это первый урок из серии видеоуроков, посвященных задачам B13. Перед нами стандартная задача, которую часто дают на пробниках и контрольных работах. Однако решать ее мы будем весьма нестандартным методом.:)
Задача B13. Дан многогранник, изображенный на рисунке. Все двугранные углы прямые. Найдите, насколько расстояние между вершинами
A
и C2 отличается от квадрата расстояния между вершинами
E
и G1. В ответ запишите положительное число.

Для решения любых таких задач нам потребуется обобщенная теорема Пифагора. Давайте отмотаем время назад и вспомним, что такое обычная теорема Пифагора. У нас есть прямоугольный треугольник с катетами
a
,
b
и гипотенузой
c
:

В этом случае квадрат гипотенузы равен сумме квадратов катетов:
c
2 =
a
2 +
b
2
Теорема Пифагора в пространстве
Но все это рассматривается лишь на плоскости, потому что треугольник — это плоская фигура. Однако та же самая формула работает и в пространстве.
Теорема Пифагора в пространстве. Рассмотрим прямоугольный параллелепипед, или, просто говоря, кирпич. Такой параллелепипед однозначно задается своими сторонами
a
,
b
и
c
. Кроме того, у него есть главная диагональ. Эта диагональ соединяет наиболее удаленные точки параллелепипеда. Разумеется, если параллелепипед прямоугольный, то таких диагоналей сразу несколько, при этом все они будут равны и будут считаться по одной и той же формуле.
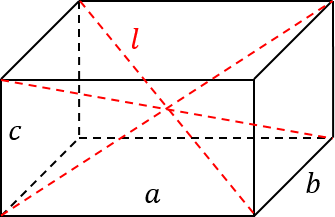
Диагональ обозначим буквой
l
. В этом случае можно записать формулу:
l
2 =
a
2 +
b
2 +
c
2
Как связана теорема Пифагора и расстояния между точками в пространстве
Возможно, кто-то сейчас спросит: а какое отношение диагональ, тем более, в параллелепипеде имеет к нашему прямоугольному треугольнику со сторонами
a
,
b
и
c
? Отношение, на самом деле, самое прямое. Давайте достроим наш треугольник до прямоугольника, и получим, что гипотенуза
c
является диагональю на прямоугольнике.
Таким образом, перед нами, по сути, аналог теоремы Пифагора для трехмерного пространства. Давайте немножко перепишем ее:
![]()
Внимательные ученики наверняка заметят, что эта формула очень похожа на формулу расстояния в трехмерном пространстве между точками
a
и
b
. Разумеется, при условии, что точка
A
лежала бы в начале координат, а точка
B
имела координаты, равные длинам сторон нашего параллелепипеда:
A
= (0; 0; 0);
B
= (
a
,
b
,
c
).
Однако ничего удивительного в этом нет, потому что длина диагонали
l
— это как раз и есть расстояние между наиболее удаленными точками параллелепипеда.
Метод обхода точек
Но хватит теории, давайте перейдем непосредственно к нашей задаче. Итак, в первую очередь нужно найти расстояние от точки
A
до точки
C
2. И вот для того, чтобы найти это расстояние, сейчас мы воспользуемся замечательным приемом, который называется обход точек.
Метод обхода точек заключается в следующем:
- Построим систему координат с осями, параллельными ребрам нашего многогранника. Назовем эти оси x, y и z.
- А теперь давайте поставим ручку в нашу точку A и попытаемся каким-то образом, двигаясь по ребрам, добраться до точки C
2.
Нахождение диагонали методом обхода точек
Разумеется, последовательность осей может быть любой, решение и ответ от этого не изменится. И двигаться из одной точки в другую тоже можно по-разному. Например, можно идти к точке
B
, затем к точке
C
, затем вверх до точки
B
2 и, наконец, двигаться вдаль — и мы попадем в точку
C
2:
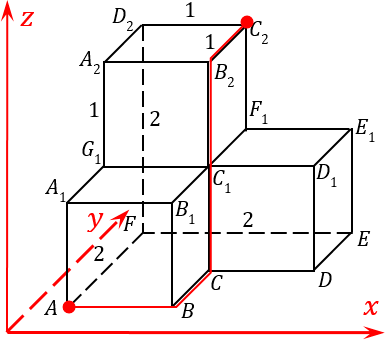
Давайте разметим, полученный нами путь:
- Из точки A в точку B мы двигались вдоль оси x в положительном направлении. Запишем: 1x;
- От точки B в точку C мы двигались вдоль оси игрек опять же по положительному направлению, то есть вглубь. Так и запишем 1y;
- Затем мы шагнули на два шага вверх из точки C в точку B
2. так и напишем: 2z; - Еще один шаг из точки B
2 в точку C
2 вдоль y, т. е. вглубь нашего рисунка. Запишем: 1y.
А теперь, когда мы отметили каждое звено нашей ломанной, соединяющие точки
A
и
C
2, выпишем, сколько шагов мы получили вдоль каждой координатной оси с учетом знаков:
- x: 1;
- y: 1 + 1 = 2;
- z: 2.
Теперь возвращается к нашей обобщенной теореме Пифагора и замечаем, что оси
x
,
y
и
z
— это, по сути,
a
,
b
и
c
, т. е. длины сторон параллелепипеда. Следовательно, мы можем посчитать длину диагонали этого параллелепипеда:
![]()
Вот и все! Мы получили расстояние от точки
A
до
C
2, согласно рисунку нашего многогранника.
Диагональ параллелепипеда не зависит от маршрута обхода
Однако внимательные ученики спросят: а что будет, если мы пойдем по другому пути? Ведь от точки
A
до точки
C
2 можно идти и другим путем: сначала вверх до точки
A
1, затем вглубь до точки
G
1, затем вверх до точки
A
2, затем снова в глубину до точки
D
2, и, наконец вправо до точки
C
2:
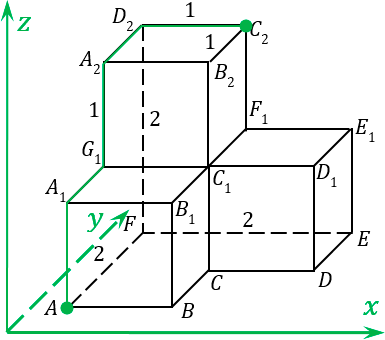
Получили совсем другой маршрут, и возникает логичный вопрос: не будет длина на этом маршруте иметь совсем другое значение координат
x
,
y
и
z
, и, соответственно, другое значение
l
? Давайте проверим.
Размечаем наш второй маршрут:
- из точки A в точку A
1 мы попадаем, смещением оси z на единичку: 1z; - из точки A
1 в точку G
1 мы попадаем, смещением по y на единичку: 1y; - из точки G
1 в точку A
2 — смещение по z: 1z; - из точки A
2 в точку D
2 — смещение по y: 1y; - от D
2 до C
2 — смещение вправо, т.е. в положительную сторону по x: 1x.
Выписываем полученные смещения:
- x: 1
- y: 1 + 1 = 2
- z: 1 + 1 = 2
Итого выражение для диагонали
l
получилось в точности тем же самым:
![]()
Таким образом, мы убедились, что итоговое значение величины
l
, т. е. расстояние между точками
A
и
C
2 не зависит от того, каким маршрутом мы будем идти из одной точки в другую. Следовательно, при решении реальных задач вы вправе выбрать любой маршрут, который будет удобен именно вам. И вообще, тот факт, что расстояние между двумя точками не зависит от того, как это расстояние мерить, на самом деле вполне логичен. Мы же занимаемся математикой, а не гаданием на кофейной гуще. Поэтому, по какому бы пути мы не пошли, ответ получится одним и тем же.
Расстояние между двумя точками в пространстве не зависит от того, как мы это расстояние считаем. Если все расчеты выполнены правильно, ответ получится одним и тем же.
Вычисление квадрата расстояния методом обхода точек
Возвращаемся к нашему заданию и переходим ко второй его части. Нужно найти расстояние между точкой
E
и точкой
G
1. Опять предлагаю воспользоваться методом обхода точек. Начнем путь от точки
E
, будем двигаться к точке
D
, потом из точки
D
в точку
D
1, и потом от
D
1 напрямую в точку
G
1:
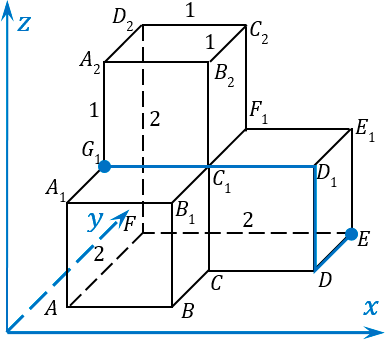
Размечаем нашу ломанную:
- из точки E в точку D мы попадаем смещением по оси y на единицу в сторону, противоположную положительному направлению оси: -1y;
- затем мы поднимаемся вверх на одну единицу по оси z, т. е. этот отрезок ломанной обозначаем как 1z;
- потом мы смещаемся влево из точки D
1 в точку G
1 на две единицы вдоль оси x и получаем -2x.
Давайте запишем, что у нас получилось:
- x: -2
- y: -1
- z: 1
По каждой из осей зафиксировано лишь одно смещение, ничего складывать, как в предыдущих случаях, не надо. Просто находим длину отрезка, соединяющего точки
E
и
G
1. Давайте назовем этот отрезок
l
2. Его длина равна:
![]()
Окончательное решение задачи B13
Вспоминаем, что от нас требуется найти в условии задачи. А от нас требуется квадрат расстояния между этими вершинами. Следовательно, нам нужна величина:
l
2
2 = 6
При произведении в квадрат корень исчезает.
Внимательно читайте условие задачи. Недостаточно просто найти длину отрезка или значение переменной — нужно предъявить именно ту величину, которую у нас спрашивают.
Осталось найти ту самую разницу, которую от нас требуют найти в условии задачи. Назовем ее ∆:
∆ = 6 − 3 = 3
Вот мы и нашли ответ — он равен 3.
Ключевой прием — обход точек
Еще раз — ключевая идея решения всей этой задачи. Она состоит в том, чтобы прямо на рисунке начертить путь из одной искомой точки в другую и посмотреть: вдоль каких координатных осей выполняется смещение и насколько. Затем мы выписываем эти смещения и считаем общее расстояние по обобщенной теореме Пифагора.
При этом возникает замечательный эффект: итоговое расстояние, которое мы считаем, не зависит от того, какой маршрут обхода мы выберем. В любом случае, как бы мы ни шли из одной точки в другую, расстояние получится одним и тем же. Разумеется, при условии, что все вычисления будут выполнены верно.
Аналогичным образом мы считаем второе расстояние. Пусть вас совершенно не смущает, что тут получаются отрицательные координаты, потому что при возведении в квадрат минусы сжигаются. Наконец, остается сосчитать ту самую разницу, которую требуется найти в условии задачи. Тут вообще все очень просто, и никаких дополнительных пояснений не требуется.
Краткая сводка по задачам B13
Итак, мы решили задачу B13 мы будем методом обхода точек. Давайте еще раз посмотрим, из каких шагов состояло наше решение:
- Добавить к рисунку оси координат, параллельные ребрам многогранника;
- Начертить «траекторию движения» от одной точки до другой, двигаясь исключительно по ребрам исходного многогранника;
- Выяснить, вдоль какой оси происходит смещение на каждом отрезке полученной ломаной, и посчитать общее смещение;
- Найти итоговое расстояние по обобщенной теореме Пифагора: l
2 = a
2 + b
2 + c
2, где a, b, c — суммарные смещения вдоль каждой из осей.
Но что будет, если выбрать другой маршрут? Не случится ли так, что при этом возникнут другие суммарные смещения и, следовательно, другое расстояние? Спешу вас обрадовать: суммарные смещения и расстояние между точками не зависит от выбранного маршрута. Мы убедились в этом лично, когда рассмотрели альтернативный маршрут обхода.
В общем, чертите путь так, как вам удобно — ответ всегда будет одним и тем же. В этом и состоит прелесть метода обхода точек.
Смотрите также:
- Обход точек в стереометрии — 2

- Разбор задачи 8 из ЕГЭ на площадь полной поверхности призмы/параллелепипеда.

- Решение ЕГЭ-2011: вариант 1, часть B

- Метод коэффициентов, часть 1

- Задача B5: площадь сектора

- Решение задач на движение по воде

Нахождение длины вектора, примеры и решения
Длина вектора – основные формулы
Длину вектора a → будем обозначать a → . Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.
Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат O x y . Пусть в ней задан некоторый вектор a → с координатами a x ; a y . Введем формулу для нахождения длины (модуля) вектора a → через координаты a x и a y .
От начала координат отложим вектор O A → = a → . Определим соответственные проекции точки A на координатные оси как A x и A y . Теперь рассмотрим прямоугольник O A x A A y с диагональю O A .
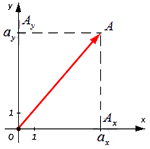
Из теоремы Пифагора следует равенство O A 2 = O A x 2 + O A y 2 , откуда O A = O A x 2 + O A y 2 . Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что O A x 2 = a x 2 и O A y 2 = a y 2 , а по построению длина O A равна длине вектора O A → , значит, O A → = O A x 2 + O A y 2 .
Отсюда получается, что формула для нахождения длины вектора a → = a x ; a y имеет соответствующий вид: a → = a x 2 + a y 2 .
Если вектор a → дан в виде разложения по координатным векторам a → = a x · i → + a y · j → , то вычислить его длину можно по той же формуле a → = a x 2 + a y 2 , в данном случае коэффициенты a x и a y выступают в роли координат вектора a → в заданной системе координат.
Вычислить длину вектора a → = 7 ; e , заданного в прямоугольной системе координат.
Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатам a → = a x 2 + a y 2 : a → = 7 2 + e 2 = 49 + e
Формула для нахождения длины вектора a → = a x ; a y ; a z по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)
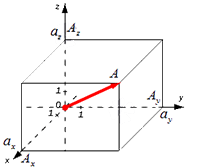
В данном случае O A 2 = O A x 2 + O A y 2 + O A z 2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда O A = O A x 2 + O A y 2 + O A z 2 . Из определения координат вектора можем записать следующие равенства O A x = a x ; O A y = a y ; O A z = a z ; , а длина ОА равна длине вектора, которую мы ищем, следовательно, O A → = O A x 2 + O A y 2 + O A z 2 .
Отсюда следует, что длина вектора a → = a x ; a y ; a z равна a → = a x 2 + a y 2 + a z 2 .
Вычислить длину вектора a → = 4 · i → – 3 · j → + 5 · k → , где i → , j → , k → – орты прямоугольной системы координат.
Дано разложение вектора a → = 4 · i → – 3 · j → + 5 · k → , его координаты равны a → = 4 , – 3 , 5 . Используя выше выведенную формулу получим a → = a x 2 + a y 2 + a z 2 = 4 2 + ( – 3 ) 2 + 5 2 = 5 2 .
Длина вектора через координаты точек его начала и конца
Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.
Итак, даны точки с заданными координатами A ( a x ; a y ) и B ( b x ; b y ) , отсюда вектор A B → имеет координаты ( b x – a x ; b y – a y ) значит, его длина может быть определена по формуле: A B → = ( b x – a x ) 2 + ( b y – a y ) 2
А если даны точки с заданными координатами A ( a x ; a y ; a z ) и B ( b x ; b y ; b z ) в трехмерном пространстве, то длину вектора A B → можно вычислить по формуле
A B → = ( b x – a x ) 2 + ( b y – a y ) 2 + ( b z – a z ) 2
Найти длину вектора A B → , если в прямоугольной системе координат A 1 , 3 , B – 3 , 1 .
Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим A B → = ( b x – a x ) 2 + ( b y – a y ) 2 : A B → = ( – 3 – 1 ) 2 + ( 1 – 3 ) 2 = 20 – 2 3 .
Второй вариант решения подразумевает под собой применение данных формул по очереди: A B → = ( – 3 – 1 ; 1 – 3 ) = ( – 4 ; 1 – 3 ) ; A B → = ( – 4 ) 2 + ( 1 – 3 ) 2 = 20 – 2 3 . –
Ответ: A B → = 20 – 2 3 .
Определить, при каких значениях длина вектора A B → равна 30 , если A ( 0 , 1 , 2 ) ; B ( 5 , 2 , λ 2 ) .
Для начала распишем длину вектора A B → по формуле: A B → = ( b x – a x ) 2 + ( b y – a y ) 2 + ( b z – a z ) 2 = ( 5 – 0 ) 2 + ( 2 – 1 ) 2 + ( λ 2 – 2 ) 2 = 26 + ( λ 2 – 2 ) 2
Затем полученное выражение приравняем к 30 , отсюда найдем искомые λ :
26 + ( λ 2 – 2 ) 2 = 30 26 + ( λ 2 – 2 ) 2 = 30 ( λ 2 – 2 ) 2 = 4 λ 2 – 2 = 2 и л и λ 2 – 2 = – 2 λ 1 = – 2 , λ 2 = 2 , λ 3 = 0 .
Ответ: λ 1 = – 2 , λ 2 = 2 , λ 3 = 0 .
Нахождение длины вектора по теореме косинусов
Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.
Пусть заданы длины двух векторов A B → , A C → и угол между ними (или косинус угла), а требуется найти длину вектора B C → или C B → . В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ A B C , вычислить длину стороны B C , которая и равна искомой длине вектора.
Рассмотрим такой случай на следующем примере.
Длины векторов A B → и A C → равны 3 и 7 соответственно, а угол между ними равен π 3 . Вычислить длину вектора B C → .
Длина вектора B C → в данном случае равна длине стороны B C треугольника △ A B C . Длины сторон A B и A C треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов: B C 2 = A B 2 + A C 2 – 2 · A B · A C · cos ∠ ( A B , → A C → ) = 3 2 + 7 2 – 2 · 3 · 7 · cos π 3 = 37 ⇒ B C = 37 Таким образом, B C → = 37 .
Итак, для нахождения длины вектора по координатам существуют следующие формулы a → = a x 2 + a y 2 или a → = a x 2 + a y 2 + a z 2 , по координатам точек начала и конца вектора A B → = ( b x – a x ) 2 + ( b y – a y ) 2 или A B → = ( b x – a x ) 2 + ( b y – a y ) 2 + ( b z – a z ) 2 , в некоторых случаях следует использовать теорему косинусов.
Длина вектора — основные формулы
Время чтения: 16 минут
Основные понятия вектора
Для того чтобы приступить к разбору формул нахождения длины вектора, необходимо разобраться в основных понятиях и определениях векторов.
Понятие вектора получило широкое распространение в 19 веке, в математических науках, особенно в таком её разделе, как «Комплексные числа».
Вектор — это отрезок с определённой длиной и направлением.
Графическое изображение вектора – отрезок который имеет указание направления в виде стрелки.
Вектор, который будет иметь начальную точку Х и конец в точке А, правильно обозначать ХА, с верхним подчёркиванием или стрелочкой, а также допустимо прописывать одной прописной буквой.
Длину вектора (модуль), определяет числовое значение длины отрезка, имеющего направление. Обозначается длинна двумя вертикальными отрезками |ХА|.
- Понятие нулевого вектора. Такое название получил вектор, у которого и начало, и конец находятся в одной точке. Обозначение он имеет в виде цифры ноль с верхним подчёркивание, а длина равна нулю.
- Коллинеарные вектора. Одна прямая может содержать несколько векторов, такие векторы получили название коллинеарных. Также коллинеарными считаются векторы на параллельных прямых.
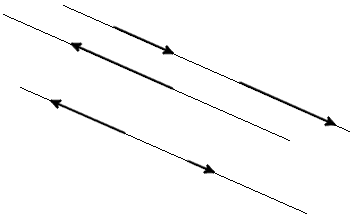
- Сонаправленные. Два коллинеарных вектора считаются сонаправленными, если имеют одно направление.
- Противоположно направленные. Вектора, с направлениями в разные стороны, и являются коллинеарными, называют противоположно направленными.
- Компланарные вектора. Такими векторами называют, те что лежат в одной плоскости
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.
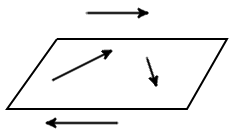
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.
Вектора могут находится не только на плоскости, но и в пространстве, от этого расположения будет зависеть какую формулу необходимо использовать для нахождения их длины или модуля. Стоит также отметить, что вектора могут быть равными, при этом они должны иметь одно направление, одинаковые длины и быть коллинеарными. Существует понятие единичного вектора, таким он будет являться если равен единице измерения.
Как найти длину вектора
Модуль вектора а будем обозначать  .
.
Для того чтобы найти модуль вектора или его длину, на плоскости по координатам, необходимо рассмотреть вектор используя прямоугольную декартову систему координат Оxy. Допустим в данной системе будет задан, так вектор  имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора
имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора  , через известные нам координаты aₓ и aᵧ.
, через известные нам координаты aₓ и aᵧ.
На взятой системе координат, от её начала отложим вектор
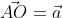 В соответствии с проекцией точки А возьмём и определим Aₓ и Aᵧ на оси координат. Рассмотрим полученный прямоугольник ОAₓ и АAᵧ с диагональю ОА.
В соответствии с проекцией точки А возьмём и определим Aₓ и Aᵧ на оси координат. Рассмотрим полученный прямоугольник ОAₓ и АAᵧ с диагональю ОА.
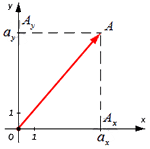
Далее используя теорему Пифагора мы получим равенство АО² = ОAₓ² и OAᵧ², отсюда следует
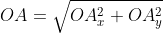
Теперь в соответствии с определением вектора относительно прямоугольной оси координат выходит, что ОAₓ² = aₓ² и также для OAᵧ² = aᵧ² , а так как на построенном прямоугольнике мы видим, что ОА равна длине вектора 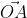 получаем
получаем
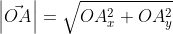
Из вышесказанного выходит, что для того чтобы найти длину вектора с точками (aₓ ; aᵧ), выводим следующую формулу:

Когда вектор  дан в формате разложения по координатным векторам
дан в формате разложения по координатным векторам 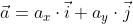 , то вычислить его можно по той же формуле
, то вычислить его можно по той же формуле  , в таком варианте коэффициент aₓ и aᵧ будут выражать в роли координат
, в таком варианте коэффициент aₓ и aᵧ будут выражать в роли координат  , в данной системе координат.
, в данной системе координат.
Чтобы рассчитать длину  = (3, √x), расположенного в прямоугольной системе координат.
= (3, √x), расположенного в прямоугольной системе координат.
Чтобы найти модуль вектора используем ранее приведённую формулу

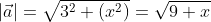
Ответ: 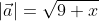
Существуют также формулы вычисления длины вектора в пространстве, они выводятся аналогично тем, что в системе координат на плоскости. Если взять вектор  =(aₓ ; aᵧ ; a
=(aₓ ; aᵧ ; a  )
)
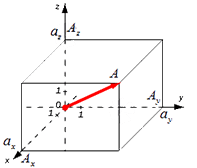
В таком случае ( AO^2=OA_x^2+OA_y^2+OA_z^2 ) (из рисунка видно, что АО – диагональ прямоугольного параллелепипеда), поэтому
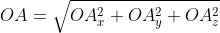
из определения получаются равенства ОAₓ=aₓ; OAᵧ=aᵧ; OA =a
=a  , а значение длины ОА совпадает с длиной вектора, которую необходимо найти. Из этого следует:
, а значение длины ОА совпадает с длиной вектора, которую необходимо найти. Из этого следует:
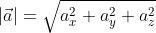
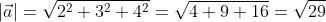
Ответ: 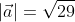
Длина вектора через координаты точек начала и конца
Ранее мы рассмотрели формулы, которые позволят находить длину вектора используя при этом координаты. Рассматривались примеры в трёхмерном пространстве на плоскости. Используя данные формулы можно найти длину вектора, если известны координаты точек его начала и конца.
Возьмём точки с обозначенными координатами начала A(aₓ ; aᵧ) и конца В(bₓ ; bᵧ), из чего следует, что вектор  имеет координаты (bₓ-aₓ ; bᵧ-aᵧ), поэтому его длину мы выразим в формуле
имеет координаты (bₓ-aₓ ; bᵧ-aᵧ), поэтому его длину мы выразим в формуле
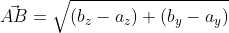
При этом формула вычисления длины вектора  для трёхмерного пространства, с координатами
для трёхмерного пространства, с координатами 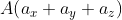 и
и 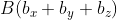 ), будет следующей:
), будет следующей:
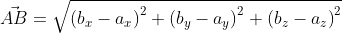
Для прямой системы координат, найти длину вектора ( overrightarrow) , где A(1,√3) B(-3,1)
Решение
Применив формулу, для нахождения длины вектора, с известными координатами точек начала и конца, в плоской системе координат, выходит:
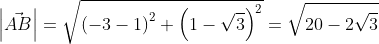
Существует второй вариант решения, где формулы применяются по очереди:
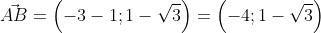
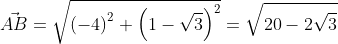
Ответ: 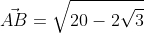
Найти, решения, при подстановке которых, длина вектора будет равна корню из тридцати, при координатах точек А (0,1,2) и В (5,2,(λ^2))
В первую очередь представим длину вектора в виде формулы.
( left|vecright|=sqrt<left ( b_x-a_x right )^2+ left ( b_y-a_y right )^2 + left ( b_z-a_z right )^2>)
(=sqrt <left ( 5-0 right )^2+ left ( 2-1 right )^2 + left ( lambda^2 -2right )^2>= sqrt<26 + left ( lambda^2 -2right )^2>)
Теперь приравняем полученное выражение к корню из тридцати и найдём неизвестное значение, решив полученное уравнение.
( sqrt<26+left(lambda^2-2right)^2>=sqrt <30>)
( 26+left(lambda^2-2right)^2=30 )
( left(lambda^2-2right)^2=4 )
( lambda^2-2=2 ) или ( lambda^2-2=-2 ) ( lambda_1=-2, lambda_2=2, lambda_3=0. )
Ответ: ( lambda_1=-2, lambda_2=2, lambda_3=0. )
Длина вектора по теореме косинусов
Так как бывают случаи, когда не известны координаты точек вектора, необходимо искать другие варианты, при помощи которых можно найти длину вектора. Таким способов может стать применение теоремы косинусов.
К примеру, нам известны длины двух векторов (overrightarrow) и (overrightarrow) , а также угол между ними, или его косинус. При этом необходимо найти длину вектора ( overrightarrow ) , в таком варианте задания необходимо воспользоваться теоремой косинусов, представив треугольник АВС. В данном треугольнике мы будем искать сторону ВС, она и будет равна длине искомого вектора. Подробнее рассмотрим на примере.
Даны длины двух векторов ( overrightarrow) и ( overrightarrow) 2 и 4 соответственно, а угол между ними равен ( frac<pi> <3>) . необходимо найти длину ( overrightarrow).
В нашем примере длины векторов и длины сторон треугольника АМК совпадают. Две из сторон нам известны это АК и АМ, а также известен угол треугольника, находящийся между этими сторонами. Используя теорему косинусов получим:
( KM^2=AK^2+AM^2-2cdot AKcdot AMcdotcosfrac<pi><3>)
(=2^2+4^2-2cdot2cdot4cdotcosfrac<pi><3>)
(=4+16-16cosfrac<pi><3>)
(=20-8=12 )
Получается (KM=sqrt <12>)
Ответ: ( left|overrightarrowright|=sqrt <12>)
Теперь мы видим, что для нахождения длины вектора существует несколько формул, которыми можно воспользоваться в зависимости от известных параметров.
длина вектора формула для трёхмерного пространства;
длина вектора формула по известным координатам начала и конца вектора находящегося пространстве; ( left|vecright|=sqrt<left ( b_z-a_z right )^2+ left ( b_y-a_y right )^2>) если известны координаты начала и конца вектора на плоскости.
Существует также формула длины вектора перемещения: ( left|vecright|=sqrt< s_x^2+s_y^2>) чаще такая формула применима в физике, для того чтобы узнать длину пути материальной точки.
В случае если известен угол, между двумя векторами, можно использовать теорему Пифагора.
Применение векторов в других сферах
Понятие и вычисление вектора важно не только в математике, но и других науках:
- в физике. Для визуального изображения таких понятий как скорость, сила, ускорение и т.д. А также векторы помогают моделировать физические процессы;
- в химии. Для изображения химических процессор. При помощи векторов изображают движение электронов и других частиц;
- в биологии. Биологические процессы, также имеют графическое изображение при помощи векторов. К примеру перенос паразитов;
- географии. Вектором обозначается движение воздушных масс, или течение реки;
Векторы используются не только в науках, но и различных отраслях и профессиях. В судоходстве и аэрофлоте, архитектуре и конструировании, а также многих других областях. Для того чтобы найти длину вектора, мы можем использовать одну из формул, в зависимости от того, что нам о нём известно, и в каком пространстве или плоскости находится неизвестный вектор.
Как найти длину векторов в параллелепипеде
4.6. Задачи с решениями
1. В параллелепипеде обозначим . Выразить через векторы a, b, с диагонали параллелепипеда и диагонали граней.
Решение. Сделаем чертёж. Пользуясь правилом сложения векторов, получаем:
AC = AB + AD = b + с, AC1 = AA1 + AC = a + b + с .
Из того же треугольника AA1C получаем: A1C = AC — AA1 = b + с — a.
Чтобы найти B1C, заметим, что B1C = A1D, так как у этих векторов совпадают и длины, и направления. Поэтому B1C = A1D = AD — AA1 = с — a.
Аналогично: DC1 = AB1 = AA1 + AB = a + b .
2. Найти длину и направляющие косинусы вектора AB, если его начало и конец находятся в точках A(7, 6), B(2 — 6).
Решение. Так как каждая точка задана двумя координатами, то рассматривается вектор на плоскости. Находим его координаты, вычитая из координат точки B (конца вектора) координаты точки A (начала вектора): AB = (2 — 7, —6 — 6) = (—5, —12). Находим длину: |AB | = 13, направляющие косинусы: .
3. Найти координату z вектора a = (1, —3, z), если известно, что она отрицательна, а модуль |a| = . Где окажется конец вектора a, если его отложить из точки M(5, —2, 1)?
Решение. По условию, . поэтому ZN = —8.
4. Найти расстояние между точками A(5, —2, 4) и B( —1, 0, 6).
Решение. Расстояние равно длине вектора AB. Найдём:
5. При каких p, q векторы a = (2,p, — 1), b = qi + 9j + 3k будут коллинеарными?
[spoiler title=”источники:”]
http://www.napishem.ru/spravochnik/matematika/dlina-vektora-osnovnye-formuly.html
http://www.chem-astu.ru/chair/study/algebra-geometry/?p=117
[/spoiler]
�������
� ������������� ��������������� ABCDA1B1C1D1 ��������,
��� AB = AA1 = 12 � AD = 30 . ����� M ����������� � �����
ABB1A1 �� ���������� 1 �� �������� AB � �� ������ �����������
�� ������ A � B . ����� N ����� � ����� DCC1D1 � �����������
����������� ����� M ������������ ������ ���������������. �������
����� ����������� ���� �� ����������� ��������������� ����� �������
M � N .
�������
�����������, ��� ���� ���������� ң��� A1B1 � C1D1 (��� ң���
AB � CD ). � ���� ������ (���.2) ����� ����������� ���� �����
11 + 30 + 1 = 42 .
�����������, ��� ���� ��������������� ���������� ң��� BB1 ,
B1C1 � C1D1 . ���������� ����� ����� ���ף���� ���������������,
������� �������� �������������� A1B1C1D1 � BB1C1C � �����
�������� B1C1 , ������� CDD1C1 , ������� ����� ������� D1C1
� ��������������� A1B1C1D1 , � ������� AA1B1B , ������� �����
������� BB1 � ��������������� BB1C1C . �� ������� �������� �������,
��� � ���� ������ ���������� ���� ����� =
.
���� �� ���� ��������������� ���������� ң��� AB , BC , B1C1 �
C1D1 , �� ���������� ����� ����� ��������� ��������������� (���.3), �������
�������� �������������� ABCD � BCC1B1 � ����� �������� BC ,
�������������� A1B1C1D1 � BB1C1C � ����� �������� B1C1 ,
������� CDD1C1 , ������� ����� ������� C1D1 � ���������������
A1B1C1D1 , � ������� ABB1A1 , ������� ����� ������� AB �
��������������� ABCD . �� ������� �������� �������, ��� � ���� ������ ����������
���� ����� = 40 .
����� �������, ����� �������� �� ������������� ����� ����� 40.
��������� ��������� ���� �������� �������.
�����
40.00
��������� � ���������� �������������
| web-���� | |
| �������� | ������� ����� �� ��������� �.�.������� |
| URL | http://zadachi.mccme.ru |
| ������ | |
| ����� | 8421 |
