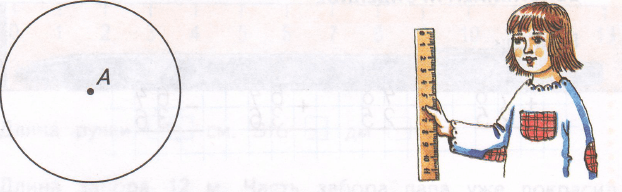Как найти радиус окружности
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
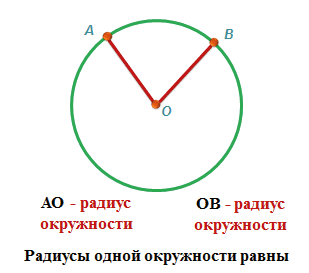
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.
Возможно тебе интересно узнать – как найти длину окружности?
Формула радиуса окружности
Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.
Если известна площадь круга
R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Если известна длина
R = P : 2 * π, где P — длина (периметр круга).
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Если известен диаметр окружности
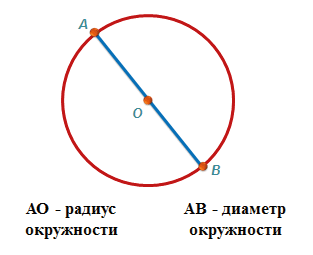
R = D : 2, где D — диаметр.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Если известна диагональ вписанного прямоугольника
R = d : 2, где d — диагональ.
Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:
d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.
Если известна сторона описанного квадрата
R = a : 2, где a — сторона.
Сторона описанного квадрата равна диаметру окружности.
Если известны стороны и площадь вписанного треугольника
R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.
Если известна площадь и полупериметр описанного треугольника
R = S : p, где S — площадь треугольника, p — полупериметр треугольника.
Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.
Если известна площадь сектора и его центральный угол
R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.
Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.
Если известна сторона вписанного правильного многоугольника
R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.
В правильном многоугольнике все стороны равны.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Конспект урока по математике на тему «Радиус и диаметр» (2 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Конспект урока математики
Тема: « Радиус и диаметр»
Форма проведения: урок изучение нового материала
Цель урока: создать условия для формирования умения чертить окружность с помощью циркуля, изучения понятия радиус и диаметр.
Образовательные: научить распознавать и изображать центр, диаметр и радиус окружности;
Развивающие: способствовать развитию логического мышления, памяти, воображения;
Воспитательные: воспитывать аккуратность, культуру общения и поведения в учебном процессе.
Оборудование: учебник математики А.Л.Чекин 2 часть , тетрадь, презентация.
Обратите внимания на слайд.
Давайте решим эту задачу: За две ручки мама заплатила 35 рублей. Одна ручка стоит 15 рублей. Сколько стоит вторая ручка?
Как ты нашел ответ?
Молодцы, давайте решим ещё одну задачу:
У Васи 16 машинок, а у Дениса на 4 машинки больше. Сколько машинок у Дениса?
Откройте тетрадь, выполняем пока и записываем число.
Дети, с какой темой вы познакомились на прошлом уроке?
Кто-нибудь может выйти и показать мне радиус?
А что такое круг? Окружность?
А кто-то сейчас может мне показать диаметр?
И так ребята, как вы думаете, какую тему мы будем изучать сегодня на уроке?
Ребята, чему мы должны научиться сегодня на уроке?
А теперь приступим к выполнению заданий.
Давайте выполним первое задание:
Прочитай задание. Запишите в тетради задание 1
Что мы должны сделать?
Давайте построим окружность с помощью циркуля
Возьмите циркуль, поставьте точку в центре окружности и поставьте иголку циркуля на центр окружности. Обозначаем её точкой O.(Ребята, с циркулем к друг другу не лезем, как начертите окружность, сразу положите циркуль в коробочку) Проведите радиус и ещё один радиус так, чтобы они находились на одной прямой.
Кто-нибудь знает, как называется такой отрезок?
Отрезок, соединяющий две точки окружности и проходящий через центр, называется диаметром.
Во сколько надо увеличить длину радиуса окружности, чтобы получить длину диаметра.
Ребята это значит что длина диаметра в два раза больше длины радиуса.
А сейчас давайте немножко отдохнём.
Если верно, то вы хлопаете в ладоши, а если неверно, то вы просто молчите.
1.Если радиус равен 8 см, то диаметр равен 16.
2. Если радиус равен 6 см, то диаметр равен 15.
3. Если радиус равен 9 см, то диаметр равен 18.
4. Если радиус равен 5 см, то диаметр равен 10.
5. Если радиус равен 7 см, то диаметр равен 16.
6. Если радиус равен 10 см, то диаметр равен 19.
Ребята диаметр обозначается буквой D.
Прочитайте задание 2 на странице 49.
На каком чертеже изображён диаметр окружности?
Почему вы выбрали его?
Поставьте иголку в центр, растворите на ширину радиуса и начертите окружность у себя в тетради.
Для того чтобы выполнить это задание надо построить одну окружность или две?
Диаметр равен сумме радиуса. Если посчитать то получится 6 см. Значит, сколько окружностей мы должны начертить?
На какой диаметр мы будем растворять циркуль?
Прочитайте задание. О чём задача?
Сформулируйте задание своими словами. Давайте заменим содержание задачи кратко.
Известно, что R(1) =12
R(2) на 3 cм меньше
На сколько D(2) меньше D(1)
Зная радиус 1 окружности, и что радиус 2 окружности на 3 см меньше. Мы можем узнать радиус 2 окружности?
Чему равен радиус 2 окружности?
Давайте узнаем диметр 1 окружности.
Как мы будем его находить?
Чему равен диаметр 1 окружности?
Зная радиус 2 окружности, мы можем узнать диаметр?
Чему равен диаметр 2 окружности?
Данное число умножаем на 2.
Зная диаметр 1 и 2 окружности мы можем узнать, на сколько D(1) окружности больше D(2) окружности?
Ребята, так, на сколько D(1) окружности больше D(2) окружности? (Если не успеют доделать дома)
Максим запиши решение на доске.
Открываем дневники, записываем домашнее задание.
Д/З: стр.50 №6, рабочая тетрадь стр. 24
-С какой темой мы сегодня познакомились?
-Что такое диаметр?
– Какой буквой обозначается диаметр?
-Как можно найти диаметр окружности?
Спасибо за урок, до свидания.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 945 человек из 80 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 318 человек из 69 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 695 человек из 75 регионов
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 481 932 материала в базе
Материал подходит для УМК
«Математика», Чекин А.Л.
Радиус и диаметр
Дистанционные курсы для педагогов
Другие материалы
- 09.11.2021
- 46
- 09.11.2021
- 178
- 09.11.2021
- 120
- 09.11.2021
- 75
- 09.11.2021
- 75
- 09.11.2021
- 306
- 09.11.2021
- 106
- 09.11.2021
- 59
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 09.11.2021 138 –> –> –> –>
- DOCX 14.7 кбайт –> –>
- Оцените материал:
Настоящий материал опубликован пользователем Стародубова Александра Алексеевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На проекте: 1 год и 4 месяца
- Подписчики: 0
- Всего просмотров: 9886
- Всего материалов: 128
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
548 курсов от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В России утвердили новые правила аккредитации образовательных учреждений
Время чтения: 1 минута
В Якутске все классы, кроме девятых и одиннадцатых, перейдут на удаленку
Время чтения: 1 минута
В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей
Время чтения: 1 минута
Крупнейшие вузы Татарстана откроют цифровые кафедры в 2022 году
Время чтения: 1 минута
В местах сдачи ЕГЭ будут применены антиковидные меры
Время чтения: 1 минута
«Учителя года» проведут открытые занятия для педагогов России
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
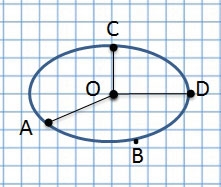
Окружность
Приступаем к изучению окружности и круга. Вспомним замкнутые и незамкнутые линии. Познакомимся с центром окружности, радиусом и диаметром и научимся определять радиус при известном диаметре и диаметр при известном радиусе.
Окружность и овал
Для начала рассмотрим рисунок и найдём окружность:
Теперь рассмотрим сходства и различия этих геометрических фигур:
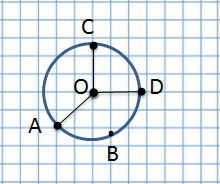
Центр в точке О
Есть точки A,B,C,D
| Овал | Окружность |
 |
|
| Сходства | |
| Различия | В овале отрезки от точки O до крайней линии разные, а в окружности – все отрезки одинаковые. |
Правило:
Окружность – это замкнутая кривая линия с точкой О в середине, которая называется центром.
Расстояния от центра до линии окружности одинаковые.
Начертить окружность можно при помощи циркуля:
А овал рисуют от руки:
Окружность и круг
Если заполнить пространство внутри окружности, то получим круг.
Круг – это часть плоскости, ограниченная окружностью.
Диаметр и радиус
Если соединить центр окружности с линией окружности, получим радиус, например, OC, OA и OD.
Радиус – длина отрезка, соединяющего центр окружности с любой точкой, лежащей на окружности. Радиус составляет половину диаметра.
Если отрезок проходит через центр и соединяет две точки на окружности – это диаметр.
Диаметр – это длина отрезка, проходящего через центр окружности и соединяющего две точки на этой окружности.
Поделись с друзьями в социальных сетях:
[spoiler title=”источники:”]
http://infourok.ru/konspekt-uroka-po-matematike-na-temu-radius-i-diametr-2-klass-5465691.html
http://budu5.com/manual/chapter/1188
[/spoiler]
- Учебники
- 2 класс
- Математика 👍
- Рудницкая
- №2
авторы: Рудницкая, Юдачева.
издательство: “Просвещение”
Раздел:
- Окружность, ее центр и радиус
ГДЗ рабочая тетрадь по математике №1 2 класс Рудницкая. Окружность, ее центр и радиус. Номер №2
- Предыдущее
- Следующее
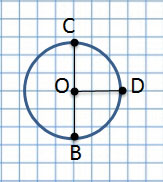
Построй радиус окружности и измерь её длину.
Длина радиуса _ см
reshalka.com
ГДЗ рабочая тетрадь по математике №1 2 класс Рудницкая. Окружность, ее центр и радиус. Номер №2
Решение
AB − радиус окружности.
Длина радиуса 2 см
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
Как найти радиус окружности
Лайфхакер собрал девять способов, которые помогут справиться с геометрическими задачами.
Выбирайте формулу в зависимости от известных величин.
Через площадь круга
- Разделите площадь круга на число пи.
- Найдите корень из результата.
- R — искомый радиус окружности.
- S — площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
Через длину окружности
- Умножьте число пи на два.
- Разделите длину окружности на результат.
- R — искомый радиус окружности.
- P — длина окружности (периметр круга).
- π (пи) — константа, равная 3,14.
Через диаметр окружности
Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.
- R — искомый радиус окружности.
- D — диаметр.
Через диагональ вписанного прямоугольника
Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.
- R — искомый радиус окружности.
- d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
- a, b — стороны вписанного прямоугольника.
Через сторону описанного квадрата
Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.
- r — искомый радиус окружности.
- a — сторона описанного квадрата.
Через стороны и площадь вписанного треугольника
- Перемножьте три стороны треугольника.
- Разделите результат на четыре площади треугольника.
- R — искомый радиус окружности.
- a, b, с — стороны вписанного треугольника.
- S — площадь треугольника.
Через площадь и полупериметр описанного треугольника
Разделите площадь описанного треугольника на его полупериметр.
- r — искомый радиус окружности.
- S — площадь треугольника.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Через площадь сектора и его центральный угол
- Умножьте площадь сектора на 360 градусов.
- Разделите результат на произведение пи и центрального угла.
- Найдите корень из полученного числа.
- R — искомый радиус окружности.
- S — площадь сектора круга.
- α — центральный угол.
- π (пи) — константа, равная 3,14.
Через сторону вписанного правильного многоугольника
- Разделите 180 градусов на количество сторон многоугольника.
- Найдите синус полученного числа.
- Умножьте результат на два.
- Разделите сторону многоугольника на результат всех предыдущих действий.
- R — искомый радиус окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✂️📌
- Как найти периметр прямоугольника
- Как научить ребёнка считать играючи
- Как перевести обычную дробь в десятичную
- 6 способов посчитать проценты от суммы с калькулятором и без
- 9 логических задач, которые по зубам только настоящим интеллектуалам
Конспект
урока математики
Тема:
«Радиус
и диаметр»
Класс: 2
Форма
проведения: урок изучение нового материала
Цель урока: создать условия для формирования
умения чертить окружность с помощью циркуля, изучения понятия радиус и диаметр.
Задачи:
Образовательные: научить
распознавать и изображать центр, диаметр и радиус окружности;
Развивающие: способствовать
развитию логического мышления, памяти, воображения;
Воспитательные: воспитывать
аккуратность, культуру общения и поведения в учебном процессе.
Оборудование: учебник
математики А.Л.Чекин 2 часть , тетрадь, презентация.
Здравствуйте, ребята.
Обратите
внимания на слайд.
Прочитайте
задачу
Давайте
решим эту задачу: За две ручки мама заплатила 35 рублей. Одна ручка стоит 15
рублей. Сколько стоит вторая ручка?
Как ты
нашел ответ?
Молодцы,
давайте решим ещё одну задачу:
У Васи
16 машинок, а у Дениса на 4 машинки больше. Сколько машинок у Дениса?
Откройте
тетрадь, выполняем пока и записываем число.
Дети, с какой темой вы
познакомились на прошлом уроке?
Кто-нибудь может выйти и
показать мне радиус?
Что это такое?
А что такое круг?
Окружность?
А кто-то сейчас может мне
показать диаметр?
.
И так ребята, как вы
думаете, какую тему мы будем изучать сегодня на уроке?
Ребята, чему мы должны
научиться сегодня на уроке?
А теперь приступим к
выполнению заданий.
Давайте выполним первое
задание:
Задание №1:
Прочитай задание.
Запишите в тетради задание 1
Что мы должны сделать?
Давайте построим окружность
с помощью циркуля
Возьмите циркуль,
поставьте точку в центре окружности и поставьте иголку циркуля на центр
окружности. Обозначаем её точкой O.(Ребята, с циркулем к друг другу не лезем,
как начертите окружность, сразу положите циркуль в коробочку) Проведите радиус
и ещё один радиус так, чтобы они находились на одной прямой.
Кто-нибудь знает, как
называется такой отрезок?
Отрезок, соединяющий две
точки окружности и проходящий через центр, называется диаметром.
Во сколько надо увеличить
длину радиуса окружности, чтобы получить длину диаметра.
Ребята это значит что
длина диаметра в два раза больше длины радиуса.
А сейчас давайте немножко
отдохнём.
Если верно, то вы
хлопаете в ладоши, а если неверно, то вы просто молчите.
1.Если радиус равен 8 см,
то диаметр равен 16.
2. Если радиус равен 6
см, то диаметр равен 15.
3. Если радиус равен 9
см, то диаметр равен 18.
4. Если радиус равен 5
см, то диаметр равен 10.
5. Если радиус равен 7
см, то диаметр равен 16.
6. Если радиус равен 10
см, то диаметр равен 19.
Ребята диаметр
обозначается буквой D.
Задание №2
Прочитайте задание 2 на
странице 49.
На каком чертеже
изображён диаметр окружности?
Почему вы выбрали его?
Поставьте иголку в центр,
растворите на ширину радиуса и начертите окружность у себя в тетради.
Задание №3
Прочитайте задание.
Для того чтобы выполнить
это задание надо построить одну окружность или две?
Диаметр равен сумме
радиуса. Если посчитать то получится 6 см. Значит, сколько окружностей мы
должны начертить?
На какой диаметр мы будем
растворять циркуль?
Задание №4
Прочитайте задание. О чём
задача?
Сформулируйте задание
своими словами. Давайте заменим содержание задачи кратко.
Известно, что R(1) =12
R(2) на 3 cм меньше
На сколько D(2) меньше
D(1)
Зная радиус 1 окружности,
и что радиус 2 окружности на 3 см меньше. Мы можем узнать радиус 2 окружности?
Каким действием?
Чему равен радиус 2
окружности?
Давайте узнаем диметр 1
окружности.
Как мы будем его
находить?
Чему равен диаметр 1
окружности?
Зная радиус 2 окружности,
мы можем узнать диаметр?
Как?
Чему равен диаметр 2
окружности?
Данное число умножаем на
2.
Зная диаметр 1 и 2
окружности мы можем узнать, на сколько D(1) окружности больше D(2) окружности?
Как?
Ребята, так, на сколько
D(1) окружности больше D(2) окружности? (Если не успеют доделать дома)
Максим запиши решение на
доске.
Открываем дневники,
записываем домашнее задание.
Д/З:
стр.50 №6, рабочая тетрадь стр. 24
-С
какой темой мы сегодня познакомились?
-Что
такое диаметр?
–
Какой буквой обозначается диаметр?
-Как
можно найти диаметр окружности?
Спасибо
за урок, до свидания.
Ученик
(186),
закрыт
6 лет назад
Дополнен 8 лет назад
сам школу закончил давно, сын не очень знает математику…. точнее на 2+ те учебники в которых былы ответы на эти вопросы сдали…. кто нибудь может дать правильный ответ??
Сашок
Знаток
(277)
8 лет назад
на 2 дели, диаметр это линия полностью проходящая через окружность а радиус это с середины линия 2 радиуса=1 диаметру 1 диаметр= 2 радиусам
Кристина
Мыслитель
(6941)
8 лет назад
Если вам дан диаметр, разделите его пополам (на 2) и получите радиус. Так как D = 2r, то r =D/2. •Например, если диаметр круга равен 10 м, то радиус круга равен 10/2 = 5 м.