Как найти длину разности векторов прямоугольника

Задание по геометрии – вектора.

Эта страница посвящена группе задач по геометрии, связанной с векторами, и является продолжением рассмотрения серии геометрических заданий, характерных для ЕГЭ и ОГЭ по математике.
Если вы не занимались другими типами этого задания, перейдите по ссылкам в конце страницы.

Задачи на вектора.

Длина отрезка называется модулем вектора. Два вектора равны, если они имеют равные модули и одинаково направлены.
Вектора обозначают либо строчными латинскими буквами a, b, c . , либо указанием концов отрезка AB, CD, MN. Чтобы отличить обозначение вектора от обозначения просто отрезка, эти символы сверху дополняются черточками или стрелочками. В печатном тексте строчные латинские буквы часто выделяют только полужирным шрифтом.

Если вектор обозначен двумя буквами (концами отрезка), то на первом месте всегда стоит начало вектора.

Задать вектор можно разными способами:
1. Графически – изобразить на координатной сетке.
2. Задать начальную и конечную точки и их координаты.
3. Задать длину отрезка и направление. Направление определяют углы с осями координат (направляющие косинусы).
4. Задать координаты вектора.

Уточним понятие координаты вектора.

На рисунке вектор AB имеет координаты (9;5). Обратите внимание, что эти числа фактически задают катеты прямоугольного треугольника, гипотенузой которого является отрезок АВ. Длина этих катетов не изменится, если мы переместим параллельным переносом отрезок, а с ним и весь треугольник, в другое место. Координаты вектора не зависят от его положения на плоскости, а только от длины отрезка и направления. Если направление вектора не совпадает с направлением оси координат, то соответствующая координата вектора будет равна длине катета со знаком “минус”.

Вектора можно складывать, вычитать, умножать на число. Для векторов также определены специальные виды умножения – скалярное произведение, результатом которого является число, и – векторное произведение, результатом которого является вектор. (Векторное произведение не входит в обязательную школьную программу по математике, но частично встречается на уроках физики, когда изучают законы индукции магнитного поля.) Операции над векторами можно производить либо координатным методом, либо графическим (правило параллелограмма, правило треугольника. ). Повторите эти правила по учебнику или справочнику и выберите себе “любимое”. Я привожу решение тем методом, который короче для конкретной задачи.

Для следующей группы задач чертёж в условии, вообще говоря, не обязателен. Если решать задачи координатным методом, то и в решении можно обойтись без чертежа, тем более, не нужна сетка. Однако лучше чертежи делать всегда, чтобы избежать нечаянных ошибок. А сетка помогает зрительно контролировать своё решение. Конечно, в том случае, если масштаб данных позволяет.

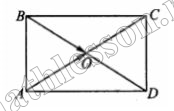
Две стороны прямоугольника ABCD равны 6 и 8.
Найдите длину вектора AC .

Длина вектора AC — равна длине отрезка AC, который является гипотенузой прямоугольного треугольника ABC с известными катетами.
AC 2 = AB 2 + BC 2 = 8 2 + 6 2 = 64 + 36 = 100; AC = 10.

Ответ: 10

Две стороны прямоугольника ABCD равны 6 и 8.
Найдите длину суммы векторов AB и AD .

По правилу параллелограмма: сумма векторов совпадает с диагональю параллелограмма, проходящей через точку, в которой совмещены начала векторов-слагаемых; начало вектора-суммы находится в точке начала обоих векторов. На рисунке это вектор AC — . Его длину мы находили в предыдущей задаче:
AC 2 = AB 2 + BC 2 = 8 2 + 6 2 = 64 + 36 = 100; AC = 10.

Ответ: 10

Две стороны прямоугольника ABCD равны 6 и 8.
Найдите длину разности векторов AB и AD .

По правилу параллелограмма: разность векторов совпадает с другой диагональю параллелограмма (соединяющей концы векторов-слагаемых, если их начала совмещены в одной точке); вектор разности направлен от вычитаемого к уменьшаемому. На рисунке это вектор DB — , направлен от D к B, так как я нахожу разность AB — − AD — .
DB 2 = AB 2 + AD 2 = 8 2 + 6 2 = 64 + 36 = 100; DB = 10.

Ответ: 10

Замечание: Ответы совпали, потому что дан один и тот же прямоугольник, а диагонали в прямоугольнике, как известно, равны.

Две стороны прямоугольника ABCD равны 6 и 8.
Найдите скалярное произведение векторов AB и AD .

Скалярное произведение двух векторов a и b находится по любой из двух формул.
1) Через координаты по формуле (a,b) = a₁·b₁ + a₂·b₂
2) Через длины векторов и угол между ними по формуле (a,b) = |a|·|b|·cosα

Способ I.
Координаты вектора AB — равны (8;0), вектора AD — равны (0;6).
Значит ( AB — , AD — ) = 8·0 + 0·6 = 0.
Способ II.
| AB — | = AB = 8, | AD — | = AD = 6, cosα = cos∠DAB = cos90° = 0.
Значит ( AB — , AD — ) = | AB — |·| AD — |·cos∠DAB = 8·6·0 = 0.

Ответ: 0

Замечание: Есть несколько способов обозначения скалярного произведения. Можно со скобками (a,b) или без них a·b _ _ , как обычное умножение.

Две стороны прямоугольника ABCD равны 6 и 8.
Диагонали пересекаются в точке O. Найдите длину суммы векторов AO и BO .

Вспомним, что диагонали прямоугольника пересекаются в его центре и в точке пересечения делятся пополам.

Способ I.
Координаты вектора AO — равны (4;3), обе положительны, потому что вектор направлен вверх, как ось Oy и вправо, как ось Ox. Координаты вектора BO — равны (-4;3), вектор направлен вверх, как ось Oy, но влево, противоположно оси Ox. Чтобы найти сумму векторов, воспользуемся тем, что при сложении векторов их соответствующие координаты складываются. Пусть вектор s(s₁;s₂) – сумма, тогда s₁ = 4 + (- 4) = 4 – 4 = 0; s₂ = 3 + 3 = 6. Квадрат длины вектора |s| 2 = s₁ 2 + s₂ 2 = 0 2 + 6 2 = 36;
длина вектора |s| = 6.

Способ II.
Чтобы решить задачу графически, надо применить к одному или к обоим векторам параллельный перенос. Для применения правила параллелограмма надо сместить их так, чтобы обе начальные точки совпали. Для применения правила треугольника надо начало одного из векторов-слагаемых совместить с концом другого. Здесь сместили вектор BO — вдоль линии ВD. На рисунке показан результат графического сложения – это вектор AD — . Как видно непосредственно по рисунку, его длина равна 6.

Ответ: 6

Две стороны прямоугольника ABCD равны 6 и 8.
Диагонали пересекаются в точке O. Найдите длину разности векторов AO и BO .

‘Способ I.
Координаты вектора AO — равны (4;3), вектора BO — равны (-4;3). Чтобы найти разность векторов, нужно найти разность их соответствующих координат. Пусть вектор d(d₁;d₂) – разность, тогда d₁ = 4 – (- 4) = 4 + 4 = 8; d₂ = 3 – 3 = 0. Квадрат длины вектора |d| 2 = d₁ 2 + d₂ 2 = 8 2 + 0 2 = 64; длина вектора |d| = 8.

Способ II.
Чтобы решить задачу графически, совмещаем начала векторов параллельным переносом обоих векторов вдоль диагоналей прямоугольника. На рисунке показан результат графического вычитания – это вектор DС — . Как видно непосредственно по рисунку, его длина равна 8.

Ответ: 8

Продолжить и повторить решение типовых задач ЕГЭ по математике на темы:

Перейдите по стрелке, чтобы найти ссылки на другие задачи ЕГЭ по математике.

Математика ОГЭ-2020. Решение заданий №19 (задания на клетчатой бумаге)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Решение заданий.docx

Решение заданий №19(задания на клетчатой бумаге)

1.Основные типы задач

Определение тангенса угла;

Определение площади фигуры (ромба, трапеции, параллелограмма, треугольника);

Определение расстояния от точки до прямой (отрезка);

Определение длины средней линии треугольника и трапеции;

Определение длины большего катета, большей диагонали;

Определение площади сложных или составных фигур;

Определение градусной меры вписанного угла.

1.Определение тангенса угла

Найдите тангенс угла А треугольника ABC, изображённого на рисунке 1.

Найдите тангенс угла AOB, изображённого
на рисунке 3.

Достроим до прямоугольного треугольника СОВ.

2. Определение площади фигуры

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм (рис. 7). Найдите его площадь.

На клетчатой бумаге с размером клетки 1×1 изображён ромб (рис. 9). Найдите площадь этого ромба.

1. Проведем диагонали.

2. Найдем площадь

3. Определение расстояния от точки до прямой (отрезка)

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C (рис. 11). Найдите расстояние от точки A до середины отрезка BC.

Построим отрезок ВС и

отметим его середину т.О.

2. Соединим т.А с т.О. Получа-

ем нужное расстояние:

4. Определение длины средней линии треугольника и трапеции

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC (рис. 14). Найдите длину его средней линии, параллельной стороне AC.

На клетчатой бумаге с размером клетки 1×1 изображена трапеция (рис. 15). Найдите длину её средней линии.

Основания трапеции соответствен-но равны 7 и 1

5. Определение длины большего катета, большей диагонали

На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник (рис. 16). Найдите длину его большего катета.

По рисунку видно, что длина

большего катета = 6.

6. Определение площади сложных или составных фигур

На клетчатой бумаге с размером клетки 1×1 изображена фигура (рис. 18). Найдите её площадь.

Посчитаем количество клеток внутри закрашенной области: их 19

Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке 19.

Решение: 1 способ (рис. 19.1)

Найдём площадь данной фигуры по формуле Пика:

Решение: 2 способ (рис.19.2)

Площадь данной фигуры

равна разности площади

квадрата и двух треугольников:

7. Определение градусной меры вписанного угла

Найдите угол ABC (рис. 20). Ответ дайте в градусах.

Проведём вспомогательное построение. Заметим, что дуга AC составляет ровно четверть окружности, следовательно, она равна 360°/4 = 90°.

Угол ABC — вписанный, поэтому он равен половине дуги, на которую опирается, значит, он равен половине дуги AC: 90°/2 = 45°.

Задачи для самостоятельно решения

Определение тангенса угла

Найдите тангенс угла А треугольника, изображённого на рисунке.

Найдите тангенс угла С треугольника ABC, изображённого на рисунке.

Найдите тангенс угла AOB, изображённого на рисунке.

Найдите тангенс углаAOB, изображённого на рисунке.

Найдите тангенс углаAOB, изображённого на рисунке.

Найдите тангенс угла AOB, изображённого на рисунке.

Найдите тангенс углаAOB.

Найдите тангенс углаAOB.

Найдите тангенс угла AOB.

Найдите тангенс угла, изображённого на рисунке.

Определение площади фигуры (ромба, трапеции, параллелограмма, треугольника)

На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.

На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.

На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник.

На клетчатой бумаге с размером клетки 1х1 изображён ромб. Найдите его площадь.

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.

На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.

Определение расстояния от точки до прямой (отрезка)

На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.

На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.

На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.

На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.

На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до прямой BC. Ответ выразите в сантиметрах.

Определение длины средней линии треугольника и трапеции

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.

На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.

На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.

Определение длины большего катета, большей диагонали

На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник. Найдите длину его большего катета.

На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник. Найдите длину его большего катета.

На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Определение площади сложных или составных фигур

На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.

Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.

Определение площади сложных или составных фигур

Найдите угол ABC . Ответ дайте в градусах.

Найдите угол ABC . Ответ дайте в градусах.

Найдите угол ABC . Ответ дайте в градусах.

Найдите угол ABC . Ответ дайте в градусах.

Найдите угол ABC . Ответ дайте в градусах.

Найдите угол ABC . Ответ дайте в градусах.

I . Определение тангенса угла

II . Определение площади фигуры (ромба, трапеции, параллелограмма, треугольника

III . Определение расстояния от точки до прямой (отрезка)

IV . Определение расстояния от точки до прямой (отрезка)

V . Определение длины большего катета, большей диагонали

VI . Определение площади сложных или составных фигур

VII .Определение площади сложных или составных фигур

Открытый банк заданий ОГЭ http :// oge . fipi . ru

Выбранный для просмотра документ мастер класс.pptx

Описание презентации по отдельным слайдам:

Решение заданий №19 (задания на клетчатой бумаге) Составила учитель математики МБОУ «Виноградовская средняя школа» Безклейная Светлана Александровна

Основные типы задач Определение тангенса угла; Определение площади фигуры (ромба, трапеции, параллелограмма, треугольника); Определение расстояния от точки до прямой (отрезка); Определение длины средней линии треугольника и трапеции; Определение длины большего катета, большей диагонали; Определение площади сложных или составных фигур; Определение градусной меры вписанного угла.

При решении задач с использованием клетчатой бумаги важно помнить, что «клеточки» должны помогать! А значит, нужно подумать как они могут помочь. По «клеточкам» легко построить прямоугольный треугольник. Следовательно, могут помочь все теоретические факты связанные с прямоугольным треугольником.

Определение тангенса угла

Определение тангенса угла

Определение тангенса угла

Определение тангенса угла

Определение тангенса угла

Определение тангенса угла

Определение тангенса угла

Определение площади фигуры

Определение площади фигуры

Определение площади фигуры

Определение площади фигуры

Определение площади фигуры

Определение расстояния от точки до прямой (отрезка) Что нужно вспомнить: Расстояние от точки до пря­мой равно перпендикуляру, опу­щен­но­му из этой точки на прямую.

Определение расстояния от точки до прямой (отрезка)

Определение расстояния от точки до прямой (отрезка)

Определение расстояния от точки до прямой (отрезка)

Определение длины средней линии треугольника и трапеции Что нужно вспомнить: Средняя линия треугольника параллельна третей стороне и равна её половине; Средняя линия трапеции равна полусумме оснований.

Определение длины средней линии треугольника и трапеции

Определение длины средней линии треугольника и трапеции

Определение длины большего катета, большей диагонали Что нужно вспомнить: Стороны прямоугольного треугольника: катеты – образуют прямой угол: гипотенуза – лежит напротив прямого угла. Диагональ – отрезок соединяющий две не соседние вершины.

Задача 1 На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета. Решение: По рисунку видно, что длина большего катета = 6. Ответ: 6. Определение длины большего катета, большей диагонали

Задача 2 На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали. Решение: По рисунку видно, что длина большей диагонали = 6. Ответ: 6. Определение длины большего катета, большей диагонали

Определение площади сложных или составных фигур

Задача 1 На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь. Решение: Посчитаем ко­ли­че­ство кле­ток внут­ри за­кра­шен­ной области: их 19 Ответ: 19. Определение площади сложных или составных фигур

Определение площади сложных или составных фигур

Определение градусной меры вписанного угла Что нужно вспомнить: Вписанный угол – угол, вершина которого лежит на окружности, а стороны её пересекают. Центральный угол – угол, вершина которого совпадает с центром окружности, а стороны её пересекают. Вписанный угол равен половине дуги, на которую опирается.

Задача 1: Найдите угол ABC. Ответ дайте в градусах. Решение: Проведём вспомогательное построение. Заметим, что дуга AC составляет ровно четверть окружности, следовательно, она равна 360°/4 = 90°. Угол ABC — вписанный, поэтому он равен половине дуги, на которую опирается, значит, он равен половине дуги AC: 90°/2 = 45°. Ответ: 45. Определение градусной меры вписанного угла

Определение градусной меры вписанного угла

Определение градусной меры вписанного угла

Определение градусной меры вписанного угла

Использованы источники: Открытый банк заданий ОГЭ http://oge.fipi.ru Решу ОГЭ Математика http://oge.sdamgia.ru

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 945 человек из 79 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 678 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 305 человек из 68 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 510 524 материала в базе

Материал подходит для УМК

«Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е.

Другие материалы

• 21.02.2020
• 108
• 2

• 19.02.2020
• 211
• 5

• 19.02.2020
• 172
• 1

• 19.02.2020
• 260
• 8

• 17.02.2020
• 197
• 1

• 13.02.2020
• 250
• 0

• 12.02.2020
• 491
• 1

• 12.02.2020
• 152
• 1

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 21.02.2020 28181
• RAR 4.2 мбайт
• 266 скачиваний
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Безклейная Светлана Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 11 месяцев
• Подписчики: 5
• Всего просмотров: 34153
• Всего материалов: 3

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Петербурге открыли памятник работавшим во время блокады учителям

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

Онлайн-семинар о снятии эмоционального напряжения у детей и подростков

Время чтения: 2 минуты

Рособрнадзор заявил о возможности переноса сроков проведения досрочного периода ГИА

Время чтения: 2 минуты

В Новосибирской области школьников переведут на удаленку

Время чтения: 1 минута

Все школы Оренбурга переводят на дистанционное обучение с 28 января

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Векторы на плоскости Работу выполнила Нина Саидзода. – презентация

Презентация была опубликована 8 лет назад пользователемКирилл Самошин

Похожие презентации

Презентация на тему: ” Векторы на плоскости Работу выполнила Нина Саидзода.” — Транскрипт:

1 Векторы на плоскости Работу выполнила Нина Саидзода

2 Содержание I.ТеорияТеория II.Задачи на тему: «Векторы на плоскости» Задача 1 Задача 2 Задача 3 III.Проверь себяПроверь себя

3 Теория «Векторы на плоскости» Сложение Правило треугольника Правило параллелограмма Свойство сложения Вычитание Правило трех точек

5 А B C Для любых трех точек А, В и С справедливо равенство:

6 Правило параллелограмма А B C

8 Вычитание векторов Разностью векторов и называется такой вектор, сумма которого с вектором равна вектору

9 Вычитание B A C

10 Правило трех точек Любой вектор можно представить как разность двух векторов, проведенных из одной точки. А B K

11 Задача 1 ОТВЕТ: 3

12 Задача 2 2. Найдите длину суммы векторов и изображенных на клетчатой бумаге с размером клетки 1×1 Ответ: 5

13 Задача 3 3.Найдите длину разности векторов и, изображенных на клетчатой бумаге с размером клетки 1×1 Ответ: 4

14 Упростите выражения: а) б) в) г) Проверь себя показать

[spoiler title=”источники:”]

http://infourok.ru/matematika-oge-2020-reshenie-zadanij-19-zadaniya-na-kletchatoj-bumage-4158853.html

http://www.myshared.ru/slide/734073/

[/spoiler]

На этой странице находится вопрос Две стороны прямоугольника abcd равны 16 и 30?, относящийся к категории
Геометрия. По уровню сложности данный вопрос соответствует знаниям
учащихся 5 – 9 классов. Здесь вы найдете правильный ответ, сможете
обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С
помощью автоматического поиска на этой же странице можно найти похожие
вопросы и ответы на них в категории Геометрия. Если ответы вызывают
сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

    Сумма векторов. Длина вектора. Дорогие друзья, в составе типов задний экзамена присутствует группа задач с векторами. Задания довольно широкого спектра (важно знать теоретические основы). Большинство решается устно. Вопросы связаны с нахождением длины вектора, суммы (разности) векторов, скалярного произведения. Так же много заданий, при решении которых необходимо осуществить действия с координатами векторов.

Теория касающаяся темы векторов несложная, и её необходимо хорошо усвоить. В этой статье разберём задачи связанные с нахождением длины вектора, также суммы (разности) векторов. Некоторые теоретические моменты:

Понятие вектора

Вектор — это направленный отрезок.

Все векторы, имеющие одинаковое направление и равные по длине являются равными.

*Все представленные выше четыре вектора равны!  

То есть, если мы будем при помощи параллельного переноса перемещать данный нам вектор, то всегда получим вектор равный исходному. Таким  образом, равных векторов может быть бесчисленное множество.

Обозначение векторов

Вектор может быть обозначен латинскими заглавными буквами, например:

При данной форме записи сначала записывается буква обозначающая начало вектора, затем буква обозначающая конец вектора.

Ещё вектор обозначается одной буквой латинского алфавита (прописной):

Возможно также обозначение без стрелок:

Сумма векторов

Суммой двух векторов АВ и ВС будет являться вектор АС.

Записывается как АВ+ВС=АС.

Это правило называется – правилом треугольника.

То есть, если мы имеем два вектора – назовём их условно (1) и (2), и конец вектора (1) совпадает с началом вектора (2), то  суммой этих векторов будет вектор, начало которого совпадает с началом вектора (1), а конец совпадает с концом вектора (2).

Вывод: если мы имеем на плоскости два вектора, то всегда сможем найти их сумму. При помощи параллельного переноса можно переместить любой из данных векторов и соединить его начало с концом другого. Например:

Перенесём вектор b, или по-другому – построим равный ему:

Как находится сумма нескольких векторов? По тому же принципу:

* * *

Правило параллелограмма

Это правило является следствием изложенного выше.

Для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.

Построим вектор равный вектору b так, чтобы его начало совпадало с концом вектора a, и мы можем построить вектор, который будет являться их суммой:

Ещё немного важной информации, необходимой для решения задач.

Вектор, равный по длине исходному, но противоположно направленный, обозначается также но имеет противоположный знак:

Эта информация крайне полезна для решения задач, в которых стоит вопрос о нахождении разности векторов. Как видите, разность векторов это та же сумма  в изменнёном виде.

Пусть даны два вектора, найдём их разность:

Мы построили  вектор противоположный вектору b, и нашли  разность.

Координаты вектора

Чтобы найти координаты вектора, нужно из координат конца вычесть соответствующие координаты начала:

То есть,  координаты вектора представляют собой пару чисел.

Если

И координаты векторов имеют вид:

То   c₁= a₁+ b₁     c₂= a₂+ b₂

Если

То   c₁= a₁– b₁      c₂= a₂– b₂

Модуль вектора

Модулем вектора называется его длина, определяется по формуле:

Формула для определения длины вектора, если известны координаты его начала и конца:

Рассмотрим задачи:

Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке О. Найдите длину разности векторов АО и ВО.

Найдём вектор, который будет являться результатом АО–ВО:

АО–ВО=АО+(–ВО)=АВ

То есть разность векторов  АО и ВО будет являться вектор АВ. А его длина равна восьми.

Ответ: 8

Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора АВ+AD.

Найдём вектор, который будет являться суммой векторов AD и AB. Вектор BC равен вектору AD. Значит AB+AD=AB+BC=AC

Длина вектора AC это длина диагонали ромба АС, она равна 16.

Ответ: 16

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО+ВО.

Найдём вектор, который будет являться суммой векторов АО и ВО. Вектор ВО равен вектору OD, значит

Длина вектора AD это длина стороны ромба. Задача сводится к нахождению гипотенузы в прямоугольном треугольнике AOD. Вычислим катеты:

По теореме Пифагора:

Ответ: 10

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО–ВО.

Найдём вектор, который будет являться результатом АО–ВО:

Длина вектора АВ это длина стороны ромба. Задача сводится к нахождению гипотенузы АВ в прямоугольном  треугольнике AOB. вычислим катеты:

По теореме Пифагора:

Ответ: 10

Стороны правильного треугольника ABC равны 3.

Найдите длину вектора АВ–АС.

Найдём результат разности векторов:

Длина вектора СВ равна трём, так как в условии сказано, что треугольник равносторонний и его стороны равны 3.

Ответ: 3

27663. Найдите длину вектора а(6;8).

Посмотреть решение

27664. Найдите квадрат длины вектора АВ.

Посмотреть решение

27707. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину вектора АС.

Посмотреть решение

27708. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину суммы векторов AB и AD.

Посмотреть решение

27709. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину разности векторов AB и AD.

Посмотреть решение

27711. Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O. Найдите длину суммы векторов АО и ВО.

Посмотреть решение

27713. Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора АВ.

Посмотреть решение

27715. Диагонали ромба ABCD равны 12 и 16.

Найдите длину вектора АВ–AD.

Посмотреть решение

27716. Диагонали ромба ABCD равны 12 и 16.

Найдите длину вектора АВ–АС.

Посмотреть решение

Стороны правильного треугольника ABC равны 2√3. Найдите длину вектора АВ+АС.

Посмотреть решение

В будущем мы продолжим рассматривать задачи с векторами, не пропустите!  Задания будут связаны с координатами векторов, скалярным произведением.

На этом всё. Успеха вам!

С уважением, Александр

Вступительный экзамен по математике. Преподаватели приглашают первого абитуриента:
— Сколько будет два плюс два?
— Три! — Нет! — Пять! — Нет! — Шесть!
— Неправильно! Да… дурак, но ищущий… берем!
Заходит второй абитуриент:
— Сколько будет два плюс два?
— Три! — Нет! — Три! — Нет! — Три!
— Неправильно! Да… дурак, но настырный… берем!
Заходит третий абитуриент:
— Сколько будет два плюс два?
— Четыре, конечно!
— Да… умный. Но мест уже нет!

P.S: Буду благодарен, если расскажете о статье в социальных сетях.

mathlesson.ru

• Обо мне
• Вопрос-Ответ
• Блог
• Отзывы
• Личный кабинет

Обо мне

Вопрос-Ответ

Блог

Отзывы

Личный кабинет

Курсы по ЕГЭ

Вебинары

Варианты Ларина

Сборники Ященко

ЕГЭ профиль

ОГЭ

Поблагодарить