Теория графов. Термины и определения в картинках
Время на прочтение
5 мин
Количество просмотров 93K

В этой статье мы познакомимся с основными терминами и определениями Теории графов. Каждый термин схематично показан на картинках.
Самый объёмный модуль на курсе «Алгоритмы и структуры данных» посвящён теории графов.
Граф – это топологичекая модель, которая состоит из множества вершин и множества соединяющих их рёбер. При этом значение имеет только сам факт, какая вершина с какой соединена.
Например, граф на рисунке состоит из 8 вершин и 8 рёбер.

Очень многие задачи могут быть решены используя богатую библиотеку алгоритмов теории графов. Для этого достаточно лишь принять объекты за вершины, а связь между ними – за рёбра, после чего весь арсенал алгоритмов теории графов к вашим услугам: нахождение маршрута от одного объекта к другому, поиск связанных компонент, вычисление кратчайших путей, поиск сети максимального потока и многое другое.
В этой статье мы познакомимся с основными терминами и определениями теории графов. На курсе “Алгоритмы и Структуры данных” в компании Отус “Теория графов” изучается в самом объёмном модуле из 6 вебинаров, где мы изучаем десяток самых популярных алгоритмов.
Вершина – точка в графе, отдельный объект, для топологической модели графа не имеет значения координата вершины, её расположение, цвет, вкус, размер; однако при решении некоторых задачах вершины могут раскрашиваться в разные цвета или сохранять числовые значения.
Ребро – неупорядоченная пара двух вершин, которые связаны друг с другом. Эти вершины называются концевыми точками или концами ребра. При этом важен сам факт наличия связи, каким именно образом осуществляется эта связь и по какой дороге – не имеет значения; однако рёбра может быть присвоен “вес”, что позволит говорить о “нагруженном графе” и решать задачи оптимизации.
Инцидентность – вершина и ребро называются инцидентными, если вершина является для этого ребра концевой. Обратите внимание, что термин “инцидентность” применим только к вершине и ребру.
Смежность вершин – две вершины называются смежными, если они инцидентны одному ребру.
Смежность рёбер – два ребра называются смежными, если они инцедентны одной вершине.
Говоря проще – две вершины смежные, если они соединены ребром, два ребра смежные – если они соединены вершиной.

Петля – ребро, инцидентное одной вершине. Ребро, которое замыкается на одной вершине.
Псевдограф – граф с петлями. С такими графами не очень удобно работать, потому что переходя по петле мы остаёмся в той же самой вершине, поэтому у него есть своё название.

Кратные рёбра – рёбра, имеющие одинаковые концевые вершины, по другому их называют ещё параллельными.
Мультиграф – граф с кратными рёбрами.
Псевдомультиграф – граф с петлями и кратными рёбрами.

Степень вершины – это количество рёбер, инцидентных указанной вершине. По-другому – количество рёбер, исходящих из вершины. Петля увеливает степень вершины на 2.
Изолированная вершина – вершина с нулевой степенью.
Висячая вершина – вершина со степенью 1.

Подграф. Если в исходном графе выделить несколько вершин и несколько рёбер (между выбранными вершинами), то мы получим подграф исходного графа.

Идея подграфов используется во многих алгоритмах, например, сначала создаётся подграф их всех вершин без рёбер, а потом дополняется выбранными рёбрами.
Полный граф – это граф, в котором каждые две вершины соединены одним ребром.

Сколько рёбер в полном графе? Это известная задача о рукопожатиях: собралось N человек (вершин) и каждый с каждым обменялся рукопожатием (ребро), сколько всего было рукопожатий? Вычисляется как сумма чисел от 1 до N – каждый новый участник должен пожать руку всем присутствующим, вычисляется по формуле: N * (N – 1) / 2.
Регулярный граф – граф, в котором степени всех вершин одинаковые.

Двудольный граф – если все вершины графа можно разделить на два множества таким образом, что каждое ребро соединяет вершины из разных множеств, то такой граф называется двудольным. Например, клиент-серверное приложение содержит множество запросов (рёбер) между клиентом и сервером, но нет запросов внутри клиента или внутри сервера.

Планарный граф. Если граф можно разместить на плоскости таким образом, чтобы рёбра не пересекались, то он называется “планарным графом” или “плоским графом”.

Если это невозможно сделать, то граф называется “непланарным”.
Минимальные непланарные графы – это полный граф К5 из 5 вершин и полный двудольный граф К3,3 из 3+3 вершин (известная задача о 3 соседях и 3 колодцах). Если какой-либо граф в качестве подграфа содержит К5 или К3,3, то он является непланарным.

Путь или Маршрут – это последовательность смежных рёбер. Обычно путь задаётся перечислением вершин, по которым он пролегает.
Длина пути – количество рёбер в пути.
Цепь – маршрут без повторяющихся рёбер.
Простая цепь – цепь без повторяющихся вершин.

Цикл или Контур – цепь, в котором последняя вершина совпадает с первой.
Длина цикла – количество рёбер в цикле.
Самый короткий цикл – это петля.

Цикл Эйлера – цикл, проходящий по каждому ребру ровно один раз. Эйлер доказал, что такой цикл существует тогда, и только тогда, когда все вершины в связанном графе имеют чётную степень.

Цикл Гамильтона – цикл, проходящий через все вершины графа по одному разу. Другими словами – это простой цикл, в который входят все вершины графа.

Взвешенный граф – граф, в котором у каждого ребра и/или каждой вершины есть “вес” – некоторое число, которое может обозначать длину пути, его стоимость и т. п. Для взвешенного графа составляются различные алгоритмы оптимизации, например поиск кратчайшего пути.

Пока ещё не придуман алгоритм, который за полиномиальное время нашёл бы кратчайший цикл Гамильтона в полном нагруженном графе, однако есть несколько приближённых алгоритмов, которые за приемлимое время находят если не кратчайший, то очень короткий цикл, эти алгоритмы мы также рассматриваем на курсе Отуса – “Алгоритмы и структуры данных”.
Связный граф – граф, в котором существует путь между любыми двумия вершинами.
Дерево – связный граф без циклов.
Между любыми двумя вершинами дерева существует единственный путь.
Деревья часто используются для организации иерархической структуры данных, например, при создании двоичных деревьев поиска или кучи, в этом случае одну вершину дерева называют корнем.

Лес – граф, в котором несколько деревьев.

Ориентированный граф или Орграф – граф, в котором рёбра имеют направления.
Дуга – направленные рёбра в ориентированном графе.

Полустепень захода вершины – количество дуг, заходящих в эту вершину.
Исток – вершина с нулевой полустепенью захода.
Полустепень исхода вершины – количество дуг, исходящих из этой вершины
Сток – вершина с нулевой полустепенью исхода.

Компонента связности – множество таких вершин графа, что между любыми двумя вершинами существует маршрут.

Компонента сильной связности – максимальное множество вершин орграфа, между любыми двумя вершинами которого существует путь по дугам.
Компонента слабой связности – максимальное множество вершин орграфа, между любыми двумя вершинами которого существует путь по дугам без учёта направления (по дугам можно двигаться в любом направлении).

Мост – ребро, при удалении которого, количество связанных компонент графа увеличивается.

Это только основные термины и определения теории графов, которые мы рассматриваем на первом вебинаре модуля “Теория графов”. Цель статьи – дать наглядное и понятное представление об этих терминах, для чего и были нарисованы эти картинки.
-
Узнать о курсе подробнее
-
Записаться на интенсив: “Алгоритм сжатия данных – код Хаффмана. Создание Архиватора.”. День 1
-
Записаться на интенсив: “Алгоритм сжатия данных – код Хаффмана. Создание Архиватора.”. День 2
Как посчитать ребра графа
| Полный граф | |
|---|---|
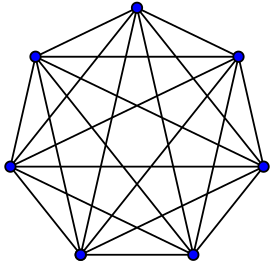 K7 , полный граф с 7 вершинами |
|
| Вершин | n |
| Рёбер | n ( n − 1 ) 2 <displaystyle <frac <2>>>  |
| Диаметр | 1 |
| Автоморфизмы | n! (Sn) |
| Хроматическое число | n |
| Хроматический индекс | n если n — нечётное, иначе n − 1 |
| Обозначение | Kn |
| Медиафайлы на Викискладе |
По́лный граф — простой неориентированный граф, в котором каждая пара различных вершин смежна. Полный граф с n <displaystyle n> 



Полный граф образуется из вершин и ребер (n-1)-симплекса.
По́лный ориенти́рованный граф — ориентированный граф, в котором каждая пара различных вершин соединена парой дуг (с различными направлениями).
Графы с K 1 <displaystyle K_<1>> 


Примеры [ править | править код ]
Ниже приведены полные графы с числом вершин от 1 до 12 и количества их рёбер.
Введение
Графы – замечательные математические объекты, с их помощью можно решать очень много различных, внешне не похожих друг на друга задач. В математике существует целый раздел – теория графов, который изучает графы, их свойства и применение. Мы же обсудим только самые основные понятия, свойства графов и некоторые способы решения задач.
Понятие графа
Рассмотрим две задачи.
Задача 1. Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Вене; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса ?
Решение: Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.

Теперь сразу видно, что долететь с Земли до Марса нельзя.
Задача 2. Доска имеет форму двойного креста, который получается, если из квадрата 4×4 убрать угловые клетки.

Можно ли обойти ее ходом шахматного коня и вернуться на исходную клетку, побывав на всех клетках ровно по одному разу ?
Решение: Занумеруем последовательно клетки доски:

А теперь с помощью рисунка покажем, что такой обход таблицы, как указано в условии, возможен:

Мы рассмотрели две непохожие задачи. Однако решения этих двух задач объединяет общая идея – графическое представление решения. При этом и картинки, нарисованные для каждой задачи, оказались похожими: каждая картинка – это несколько точек, некоторые из которых соединены линиями.
Такие картинки и называются графами. Точки при этом называются вершинами, а линии – ребрами графа. Заметим, что не каждая картинка такого вида будет называться графом. Например.если вас попросят нарисовать в тетради пятиугольник, то такой рисунок графом не будет. Будем называть что рисунок такого вида, как в предыдущих задачах, графом, если есть какая-то конкретная задача для которой такой рисунок построен.
Другое замечание касается вида графа. Попробуйте проверить, что граф для одной и той же задачи можно нарисовать разными способами; и наоборот для разных задач можно нарисовать одинаковые по виду графы. Здесь важно лишь то, какие вершины соединены друг с другом, а какие – нет. Например, граф для задачи 1 можно нарисовать по-другому:

Такие одинаковые, но по-разному нарисованные графы, называются изоморфными.
Степени вершин и подсчет числа ребер графа
Запишем еще одно определение: Степенью вершины графа называется количество выходящих из нее ребер. В связи с этим, вершина, имеющая четную степень, называется четной вершиной, соответственно, вершина, имеющая нечетную степень, называется нечетной вершиной.
С понятием степени вершины связана одна из основных теорем теории графов –теорема о честности числа нечетных вершин. Докажем ее мы немного позднее, а сначала для иллюстрации рассмотрим задачу.
Задача 3. В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими ?
Решение: Допустим, что такое соединение телефонов возможно. Тогда представим себе граф, в котором вершины обозначают телефоны, а ребра – провода, их соединяющие. Подсчитаем, сколько всего получится проводов. К каждому телефону подключено ровно 5 проводов, т.е. степень каждой вершины нашего графа – 5. Чтобы найти число проводов, надо просуммировать степени всех вершин графа и полученный результат разделить на 2 (т.к. каждый провод имеет два конца, то при суммировании степеней каждый провод будет взят 2 раза). Но тогда количество проводов получится разным  . Но это число не целое. Значит наше предположение о том, что можно соединить каждый телефон ровно с пятью другими, оказалось неверным.
. Но это число не целое. Значит наше предположение о том, что можно соединить каждый телефон ровно с пятью другими, оказалось неверным.
Ответ. Соединить телефоны таким образом невозможно.
Теорема: Любой граф содержит четное число нечетных вершин.
Доказательство: Количество ребер графа равно половине суммы степеней его вершин. Так как количество ребер должно быть целым числом, то сумма степеней вершин должна быть четной. А это возможно только в том случае, если граф содержит четное число нечетных вершин.
Связность графа
Есть еще одно важное понятие, относящееся к графам – понятие связности.
Граф называется связным, если излюбые две его вершины можно соединить путем, т.е. непрерывной последовательностью ребер. Существует целый ряд задач, решение которых основано на понятии связности графа.
Задача 4. В стране Семерка 15 городов, каждый из городов соединен дорогами не менее, чем с семью другими. Докажите, что из каждого города модно добраться в любой другой.
Доказательство: Рассмотрим два произвольных А и В города и допустим, что между ними нет пути. Каждый из них соединен дорогами не менее, чем с семью другими, причем нет такого города, который был бы соединен с обоими рассматриваемыми городами (в противном случае существовал бы путь из A в B). Нарисуем часть графа, соответствующую этим городам:

Теперь явно видно, что мы получили не менее различных 16 городов, что противоречит условию задачи. Значит утверждение доказано от противного.
Если принять во внимание предыдущее определение, то утверждение задачи можно переформулировать и по-другому: “Доказать, что граф дорог страны Семерка связен.”
Теперь вы знаете, как выглядит связный граф. Несвязный граф имеет вид нескольких “кусков”, каждый из которых – либо отдельная вершина без ребер, либо связный граф. Пример несвязного графа вы видите на рисунке:

Каждый такой отдельный кусок называется компонентой связности графа. Каждая компонента связности представляет собой связный граф и для нее выполняются все утверждения, которые мы доказали для связных графов. Рассмотрим пример задачи, в которой используется компонента связности:
Задача 5. В Тридевятом царстве только один вид транспорта – ковер-самолет. Из столицы выходит 21 ковролиния, из города Дальний – одна, а из всех остальных городов, – по 20. Докажите, что из столицы можно долететь в город Дальний.
Доказательство: Понятно, что если нарисовать граф ковролиний Царства, то он может быть несвязным. Рассмотрим компоненту связности, которая включает в себя столицу Царства. Из столицы выходит 21 ковролиния, а из любых других городов, кроме города Дальний – по 20, поэтому, чтобы выполнялся закон о четном числе нечетных вершин необходимо, чтобы и город Дальний входил в эту же самую компоненту связности. А так как компонента связности – связный граф, то из столицы существует путь по ковролиниям до города Дальний, что и требовалось доказать.
Графы Эйлера
Вы наверняка сталкивались с задачами, в которых требуется нарисовать какую-либо фигуру не отрывая карандаш от бумаги и проводя каждую линию только один раз. Оказывается, что такая задача не всегда разрешима, т.е. существуют фигуры, которые указанным способом нарисовать нельзя. Вопрос разрешимости таких задач также входит в теорию графов. Впервые его исследовал в 1736 году великий немецкий математик Леонард Эйлер, решая задачу о Кенигсбергских мостах. Поэтому графы, которые можно нарисовать указанным способом, называются Эйлеровыми графами.
Задача 6. Можно ли нарисовать изображенный на рисунке граф не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз ?

Решение. Если мы будем рисовать граф так, как сказано в условии, то в каждую вершину, кроме начальной и конечной, мы войдем столько же раз, сколько выйдем из нее. То есть все вершины графа, кроме двух должны быть четными. В нашем же графе имеется три нечетные вершины, поэтому его нельзя нарисовать указанным в условии способом.
Сейчас мы доказали теорему об Эйлеровых графах:
Теорема: Эйлеров граф должен иметь не более двух нечетных вершин.
И в заключение – задача о Кенигсбергских мостах.
Задача 7. На рисунке изображена схема мостов города Кенигсберга.
Можно ли совершить прогулку так, чтобы пройти по каждому мосту ровно 1 раз?

3. Задачи к теме “Графы”
Понятие графа.
1. На квадратной доске 3×3 расставлены 4 коня так, как показано на рис.1. Можно ли сделав несколько ходов конями, переставить их в положение, показанное на рис.2?
Решение. Занумеруем клетки доски, как показано на рисунке:

Каждой клетке поставим в соответствие точку на плоскости и, если из одной клетки можно попасть в другую ходом шахматного коня, то соответствующие точки соединим линией. Исходная и требуемая расстановки коней показаны на рисунках:
При любой последовательности ходов конями порядок их следования, очевидно, измениться не может. Поэтому переставить коней требуемым образом невозможно.
2. В стране Цифра есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два города соединены авиалинией в том и только в том случае, если двузначное число, образованное названиями городов, делится на 3. Можно ли долететь по воздуху из города 1 в город 9 ?
Решение. Поставив в соответствие каждому городу точку и соединив точки линией, если сумма цифр делится на 3, получим граф, в котором цифры 3, 5, 9 связаны между собой, но не связаны с остальными. Значит долететь из города 1 в город 9 нельзя.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9372 —  | 7304 —
| 7304 —  или читать все.
или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Класс: 7
Презентация к уроку
Загрузить презентацию (486,9 кБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Профиль класса: общеобразовательный.
Тип урока: изучение и первичное закрепление новых знаний.
Знания и умения учащихся:
- ученик знает понятия графа и мультиграфа, знаком с понятиями “вершина графа” (смежные вершины) и “ребро графа” (кратные ребра и петли);
- умеет приводить примеры использования графов в различных учебных предметах и повседневной жизни.
Образовательные:
- закрепить понятие графа, сформировать представление о степени вершины графа (четная, нечетная вершины), сформулировать определение о связности графа, рассмотреть утверждение о количестве ребер графа и теорему о четности числа нечетных вершин графа;
- отработать навыки использования теоретических знаний для решения новых задач.
Развивающие:
- развивать логическое мышление учащихся, способность к рассуждению, внимательность;
- формировать умение представлять информацию в виде графов.
Воспитательная:
- воспитывать культуру общения на уроке, взаимоуважение.
План урока
- Организационный момент (приветствие класса, подготовка к уроку, проверка домашнего задания, включающая повторение материала предыдущего урока);
- Теоретический материал (знакомство с темой предстоящего урока, объяснение нового материала и краткая запись в рабочую тетрадь новых теоретических сведений по теме урока);
- Закрепление материала (решение задач);
- Итоги урока (краткий вывод и домашнее задание).
Давайте вспомним основные понятия теории графов. Для этого проведем разминку по типу незаконченного предложения (Презентация, сл.: 2, 3, 4). Каждый ученик имеет карточки с пропущенными словами в предложение. Учитель зачитывает предложение, останавливаясь перед пропущенным словом, и выбирает ученика, который в свою очередь должен поднять карточку. Далее этот ученик читает дальше предложение, также останавливаясь перед пропущенным словом, и уже сам выбирает одноклассника для ответа и т. д. по цепочке.
Проверим в классе решение домашней задачи (Презентация, сл.: 5, 6, 7). Один ученик выходит к доске и рисует граф. Далее мы вместе проверяем ребра (дороги между городами), считаем количество выходящих ребер из каждой вершины и смотрим связи между городами.
Сегодня на уроке мы продолжим изучение графов, познакомимся с понятием “степень вершины графа” и сформулируем определение связности графа (обратим внимание на наш граф из домашнего задания и определим, является ли он связным или нет и почему). Рассмотрим утверждение о количестве ребер графа, и проверим в соответствие с этим утверждением, правильно ли мы посчитали количество ребер графа в домашней задаче. И рассмотрим теорему о четности числа нечетных вершин графа.
Количество ребер, выходящих из одной вершины, называют степенью этой вершины. Для петли будем считать, что это ребро выходит из вершины дважды (Презентация, сл. 8).
Запишем определение в рабочую тетрадь и зарисуем представленный граф, для данного графа посчитаем степень каждой вершины. Ребята смотрят на слайд и работают самостоятельно, далее вслух зачитаем степень каждой вершины.
Вершина, имеющая четную степень, называется четной вершиной, соответственно, вершина, имеющая нечетную степень, называется нечетной вершиной (Презентация, сл. 9).
Запишем определение в тетрадь и перечислим через запятую сначала четные вершины, а потом нечетные вершины для уже нарисованного графа. Проверим задание вслух.
Количество ребер графа равно половине суммы степеней его вершин. Пусть граф имеет n вершин, тогда число ребер равно:

(Презентация, сл. 10)
Запишем утверждение в рабочую тетрадь и посчитаем количество ребер графа в домашней задачке. Проверим ответ в классе. Рассмотрим задачу и ее решение на подсчет числа ребер графа без построения. (Презентация, сл. 11).
Сформулируем теорему о количестве вершин нечетной степени любого графа и запишем формулировку в рабочую тетрадь. (Презентация, сл. 12).
Теорема. Количество вершин нечетной степени любого графа всегда четно.
Доказательство: Количество ребер графа равно половине суммы степеней его вершин.
Так как количество ребер должно быть целым числом, то сумма степеней вершин должна быть четной.
А это возможно только в том случае, если граф содержит четное число нечетных вершин.
Разберем доказательство и проверим теорему на нашей домашней задачке.
Рассмотрим несколько задач.
Задача. В государстве 50 городов, из каждого города выходит 4 дороги. Сколько всего дорог в государстве.
Решение. Подсчитаем общее количество выходящих дорог из городов: 50 * 4 = 200. Однако, мы понимаем, что при подсчете каждая дорога посчитана 2 раза – она выходит из одного города и входит в другой. Значит всего дорог в два раза меньше, т.е. 100.
Задача. В классе 30 человек. Может ли быть так, что 9 человек имеют по 3 друга, 11 – по 4 друга, а 10 – по 5 друзей?
Ответ. Нет (теорема о четности числа нечетных вершин).
Сегодня мы с вами познакомились с новыми определениями, связанными с понятием графа, рассмотрели утверждение, которое помогает быстро подсчитывать число ребер графа, и сформулировали теорему, которая значительно упрощает решение многих задач. В частности, поучительная сторона этой теоремы заключается в исследовании и ответе на вопрос, возможно или нет решение данной задачи, прежде чем приступать за ее решение.
В качестве домашнего задания ученики получать карточки с тремя задачами (Презентация, сл. 13).
Информатика. Учебник для 9 класса (по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень)
§17. Графы.
Что такое граф?
Ключевые слова:
• граф • вершина • ребро • матрица смежности • степень вершины • связный граф • взвешенный граф • весовая матрица • ориентированный граф • оптимальный путь • количество путей
Давайте подумаем, как можно наглядно представить такую информацию:
От пос. Васюки три дороги идут в Солнцево, Грибное и Ягодное. Между Солнцевом и Грибным и между Грибным и Ягодным также есть дороги. Кроме того, есть дорога, которая идет из Грибного в лес и возвращается обратно в Грибное.
Нарисуйте в тетради схему дорог по этому описанию.
Можно, например, нарисовать такую схему (рис. 3.17, а).

Рис. 3.17
В информатике для исследования таких схем используют графы.
Граф — это набор вершин (узлов) и связей между ними — рёбер.
Граф, соответствующий нашей схеме дорог, показан на рис. 3.17, б, для краткости населённые пункты обозначены латинскими буквами.
Матрица смежности графа
Для хранения информации об узлах и связях показанного выше графа можно использовать таблицу такого вида (рис. 3.18).

Рис. 3.18
Единица на пересечении строки А и столбца В означает, что между вершинами А и В есть связь. Ноль указывает на то, что связи нет. Такая таблица называется матрицей смежности. Она симметрична относительно главной диагонали (см. закрашенные клетки в таблице).
Исследуйте матрицу смежности и сравните её с графом на рис. 3.17, б. Что означает единица на пересечении столбца С и строки С?
В этом графе есть петля — ребро, которое начинается и заканчивается в одной и той же вершине.
Степенью вершины называют количество рёбер, с которыми связана вершина. При этом петля считается дважды (с вершиной связаны оба конца ребра!).
Подсчитайте по матрице смежности, сколько ребёр в графе. Определите степени всех вершин. Как вы рассуждали?
Строго говоря, граф — это математический объект, а не рисунок. Конечно, его можно нарисовать на плоскости (например, как на рис. 3.17, б), но матрица смежности не даёт никакой информации о том, как именно располагать вершины друг относительно друга. Для таблицы, приведённой выше, возможны, например, такие варианты (рис. 3.19).

Рис. 3.19
Нарисуйте по матрице смежности (рис. 3.20) два разных изображения графа.

Рис. 3.20
Граф имеет 4 вершины, причём каждая вершина связана рёбрами со всеми остальными. Нарисуйте этот граф. Сколько всего рёбер в этом графе?
Граф имеет N вершин, причём каждая вершина связана рёбрами со всеми остальными. Сколько всего рёбер в этом графе?
Граф имеет 4 ребра. Чему равна сумма степеней вершин в этом графе? Зависит ли она от количества вершин?
Граф имеет N рёбер. Чему равна сумма степеней вершин в этом графе?
Попробуйте нарисовать граф с пятью вершинами, где все вершины имеют степень 3. Получилось ли у вас? Почему?
Связный граф
В графе на рис. 3.17, б все вершины связаны: между любой парой вершин существует путь — последовательность вершин, в которой каждая следующая связана ребром с предыдущей. Такой граф называется связным.
Связный граф — это граф, между любыми вершинами которого существует путь.
Теперь представьте себе, что дороги Васюки-Солнцево, Васю- ки-Грибное и Грибное-Ягодное завалило снегом (или размыло дождём) так, что по ним ни пройти, ни проехать (рис. 3.21).

Рис. 3.21
Эту схему тоже можно считать графом (она соответствует определению), но в таком графе есть две несвязанные части, каждая из которых — связный граф. Такие части называют компонентами связности.
Постройте матрицу смежности графа, изображённого на рис. 3.21.
Граф имеет 4 вершины и две компоненты связности. Какое наибольшее количество рёбер может быть в этом графе, если в нём нет петель? Нарисуйте этот граф.
Вспоминая материал предыдущего параграфа, можно сделать вывод, что дерево — это частный случай связного графа. Но у него есть одно важное свойство — в дереве нет замкнутых путей — циклов, т. е. путей, которые начинаются и заканчиваются в одной и той же вершине.
Найдите все циклы в графе на рис. 3.17.
Дерево — это связный граф, в котором нет циклов.
Взвешенный граф
Если в нашем примере нас заинтересует не только наличие дорог между посёлками, но ещё и расстояния между ними, каждой связи нужно сопоставить число — вес ребра (рис. 3.22).

Рис. 3.22
Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра.
Весом может быть не только расстояние, но и, например, стоимость проезда или другая величина.
Как хранить информацию о таком графе? Ответ напрашивается сам собой — нужно в таблицу записывать не 1 или 0, а вес ребра. Если связи между двумя узлами нет, на бумаге можно оставить ячейку таблицы пустой, а при хранении в памяти компьютера записывать в неё условный код, например, число -1 или очень большое число. Такая таблица называется весовой матрицей, потому что содержит веса рёбер. В данном случае она выглядит так (рис. 3.23).

Рис. 3.23
Так же как и матрица смежности, весовая матрица симметрична относительно диагонали.
Что означают пустые ячейки в весовой матрице?
Как по весовой матрице сразу определить, сколько рёбер в графе?
Определите по весовой матрице (рис. 3.24) длины путей ADBEC, ABDCE, DEBAC. Как вы рассуждали?

Рис. 3.24
Оптимальный путь в графе
Для того чтобы определить оптимальный (наилучший) путь между двумя вершинами графа, нужно ввести какой-то числовой показатель, по которому можно сравнивать пути — определять, какой из них лучше. Обычно для оценки пути используют сумму весов ребёр, входящих в этот путь. Например, при поиске кратчайшего пути чем меньше это значение, тем лучше.
Какие показатели вы используете в жизни для определения оптимального пути? Всегда ли самый короткий путь — самый лучший?
Если в графе немного узлов, по весовой матрице можно легко определить оптимальный путь из одной вершины в другую простым перебором вариантов. Рассмотрим граф, заданный весовой матрицей на рис. 3.25 (числа определяют стоимость поездки между соседними пунктами).

Рис. 3.25
Найдём наилучший путь из А в В — такой, при котором общая стоимость поездки минимальная.
Для решения задачи будем строить дерево перебора вариантов. Видим, что из пункта А напрямую

Рис. 3.26
Числа около рёбер обозначают стоимость поездки по этому участку, а индексы у названий узлов показывают общую стоимость проезда в данный узел из узла А. Теперь разберём варианты дальнейшего движения из узла С I tM lt;pb р (рис. 3.27).

Рис. 3.27
Почему, на ваш взгляд, на схеме не показана возможность движения из С в А?
Видим, что из С сразу можно попасть в В, стоимость проезда в этом случае равна 7.
Почему нельзя на этом остановиться, ведь путь из А в В найден?
Проверяя пути через узел В, выясняем, что можно сократить стоимость до 6 (рис. 3.28)

Рис. 3.28
Нужно ли исследовать дальше путь, содержащий цепочку ACED? Сравните стоимость этого пути и стоимость уже найденного пути из А в В.
Аналогично строим вторую часть схемы (рис. 3.29).

Рис. 3.29
Таким образом, оптимальный (наилучший) путь — ADEB, его стоимость — 3.
Нужно ли проверять пути ACED и ADEC, не дошедшие до узла В? Могут ли они улучшить результат?
Конечно, для более сложных графов метод перебора работает очень долго, поэтому используются более совершенные (но значительно более сложные) методы.
Ориентированный граф
Наверное, вы заметили, что при изображении деревьев, которые описывают иерархию (подчинение), мы ставили стрелки от верхних уровней к нижним. Это означает, что для каждого ребра указывается направление, и двигаться можно только по стрелкам, но не наоборот.
Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление.
Орграф может служить, например, моделью системы дорог с односторонним движением. Матрица смежности и весовая матрица для орграфа уже не обязательно будут симметричными.
На схеме на рис. 3.30 всего две дороги с двусторонним движением, по остальным можно ехать только в одну сторону.

Рис. 3.30
Рёбра в орграфе называют дугами. Дуга, в отличие от ребра, имеет начало и конец.
Нарисуйте граф по весовой матрице, показанной на рис. 3.31. С помощью дерева перебора найдите все возможные пути из вершины А в вершину Е, не проходящие дважды через одну и ту же вершину, и стоимости проезда по каждому из этих путей. Определите оптимальный путь из вершины А в вершину Е.

Рис. 3.31
Количество путей
Определим количество возможных путей из вершины А в вершину К для ориентированного графа, показанного на рис. 3.32.

Рис. 3.32
Так как граф ориентированный, переходить в другую вершину можно только по стрелкам.
В графе на рис. 3.32 есть одна начальная вершина А, из которой дуги только выходят. Такая вершина называется истоком. Вершина, в которую дуги только входят (и ни одна не выходит), называется конечной вершиной или стоком. В нашем графе сток — это вершина К.
По весовой матрице на рис. 3.31 найдите исток и сток в графе. Как вы рассуждали?
Будем двигаться по стрелкам от начальной вершины А. Около каждой вершины запишем количество возможных путей из вершины А в эту вершину. В вершину А существует единственный путь — пустой (никуда не ехать). Найдём все вершины, в которые можно приехать только из А: это вершины Б и Г, записываем около них количество путей 1 (рис. 3.33).

Рис. 3.33
Теперь ищем вершины, в которые можно попасть только из уже отмеченных вершин. Например, в вершину В есть один путь из А напрямую, а также по одному пути через Б и Г (так как эти вершины отмечены числом 1). Общее количество путей из А в Б равно сумме отметок предыдущих вершин: для вершины В получаем 3 пути. В вершину Ж можно попасть только из Г, поэтому число путей в Г и Ж совпадает (рис. 3.34).

Рис. 3.34
В вершину Д идёт один путь через Б и три пути через В, поэтому общее число путей — 4. Аналогично получаем 4 пути в вершину Е: 3 пути через В и один через Ж (рис. 3.35).

Рис. 3.35
Далее находим один путь из А в И (только через Ж) и 4 пути из А в 3 (все через Д). В конечную вершину К можно приехать через вершины Д (4 пути), 3 (4 пути), Е (4 пути) и И (1 путь), таким образом, общее количество различных путей равно 13 (рис. 3.36).

Рис. 3.36
Выводы
• Граф — это набор вершин (узлов) и связей между ними — рёбер.
• Матрица смежности — это таблица, в которой единица на пересечении строки и столбца обозначает ребро между соответствующими вершинами, а ноль — отсутствие ребра.
• Связный граф — это граф, между любыми вершинами которого существует путь.
• Цикл — это замкнутый путь в графе.
• Дерево — это связный граф, в котором нет циклов.
• Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра. Взвешенный граф описывается весовой матрицей.
• Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление. Рёбра орграфа называют дугами. Матрица смежности и весовая матрица орграфа могут быть несимметричными.
Нарисуйте в тетради интеллект-карту этого параграфа.
Вопросы и задания
1. Можно ли сказать, что лес (множество деревьев) — это граф? Почему?
2. Как по матрице смежности определить, есть ли петли в графе?
3. Как по весовой матрице определить длину пути в графе?
4. Когда для представления данных используются орграфы? Приведите примеры.
5. Выполните по указанию учителя задания в рабочей тетради.
Подготовьте сообщение
а) «Задача о Кёнигсбергских мостах»
б) «Решение логических задач с помощью графов»
Оглавление
§16. Списки и деревья.
§17. Графы.
§18. Игровые стратегии.

Тема ¹ 3. Графы
Содержание
|
Основные понятия и операции |
3 |
|
Графы, их вершины, ребра и дуги . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
3 |
|
Изображение графов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
4 |
|
Матрица инцидентности и список ребер . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
6 |
|
Матрица смежности графа . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
9 |
|
Маршруты, цепи и циклы |
10 |
|
Определения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
10 |
|
Связные компоненты графа . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
12 |
|
Расстояния . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
13 |
|
Задача о кратчайшем пути |
14 |
|
Постановка задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
14 |
|
Нахождение кратчайшего пути в графе с ребрами единичной длины . . . . . . . . . . . . . . . . |
15 |
|
Нахождение кратчайшего пути в графе c ребрами произвольной длины . . . . . . . . . . . . . . |
19 |
|
Транспортные сети |
22 |
|
Основные понятия . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
22 |
|
Задача о наибольшем потоке . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
25 |
|
Нахождение полного потока . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
27 |
|
Нахождение наибольшего потока . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
27 |
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

|
Транспортная задача |
30 |
|
Предметный указатель |
39 |
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

Основные понятия и операции
Графы, их вершины, ребра и дуги
Теорию графов начали разрабатывать для решения некоторых задач о геометрических конфигурациях, состоящих из точек и линий. В этих задачах несущественно, соединены ли точки конфигурации отрезками прямых или криволинейными дугами, какова длина линий и другие геометрические характеристики конфигурации. Важно лишь то, что каждая линия соединяет какие-либо две из заданных точек. Таким образом, можно дать определение графа как совокупности двух множеств V (точек) и E (линий), между элементами которых определено отношение инцидентности, причем каждый элемент e E инцидентен ровно двум элементам v0, v00 V . Элементы множества V называются вершинами графа G, элементы множества E — его ребрами. Вершины и ребра графа G называют еще его элементами и вместо v V, e E пишут соответственно v G и e G.
Внекоторых задачах инцидентные ребру вершины неравноправны, они рассматриваются в определенном порядке. Тогда каждому ребру можно приписать направление от первой из инцидентных вершин ко второй. Направленные ребра часто называют дугами, а содержащий их граф — ориентированным (граф, определенный ранее, называется неориентированным). Первая по порядку вершина, инцидентная ребру ориентированного графа, называется его началом, вторая — его концом. Говорят еще, что ребро ориентированного графа выходит из начала и входит в конец.
Вдальнейшем оказалось, что понятие графа можно применить не только при исследовании геометрических конфигураций.Особенно часто определяют графы при анализе функционирования систем. С отдельными компонентами изучаемой системы удобно связывать вершины графа, а с парами взаимодействующих компонент — его ребра. Построенный таким образом граф называют структурным графом системы..
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель
|
в) |
||
|
а) |
б) |
г) |
|
е) |
ж) |
|
|
д) |
з) |
|
|
Рис. 3.1. |
||
Изображение графов |
||
|
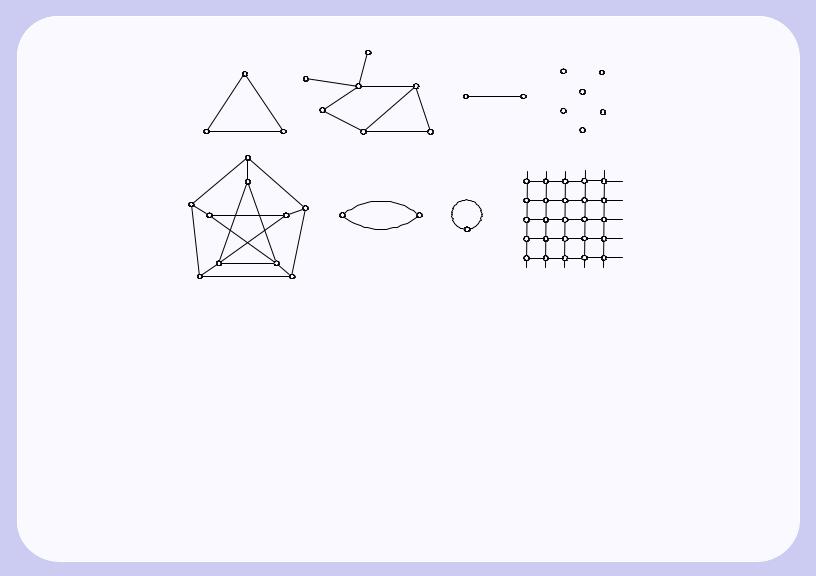
На рис. 3.1,а–з изображены некоторые неориентированные графы. Множество ребер E может быть |
||
|
пустым (см. рис. 3.1,г). Если же множество вершин V пусто, то пусто и E. Такой граф называется |
||
|
пустым. Линии, изображающие ребра графа, могут пересекаться, но точки пересечения не являют- |
||
|
ся вершинами (см. рис. 3.1,д); различные ребра могут быть инцидентны одной и той же паре вершин |
||
|
(рис. 3.1,е), в этом случае они называются кратными; граф, содержащий кратные ребра, часто называ- |
||
|
ют мультиграфом. Ребро может соединять некоторую вершину саму с собой (рис. 3.1,ж), такое ребро |
||
|
называется петлей. На рис. 3.1,з изображен фрагмент бесконечного графа. Его вершины — это точки |
||
|
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель |
|
плоскости с целыми координатами (x, y), а ребра — соединяющие их горизонтальные и вертикальные |
|||
|
отрезки длины 1. |
|||
|
Обычно рассматриваемые графы конечны, т. е. конечны множества их элементов (вершин и ребер). |
|||
|
Поэтому конечность этих графов не будет специально оговариваться. Однако некоторые понятия и |
|||
|
результаты, о которых будет идти речь, относятся к произвольным графам. |
|||
|
а) |
б) |
в) |
г) |
|
д) |
е) |
ж) |
з) |
|
Рис. 3.2. |
|||
|
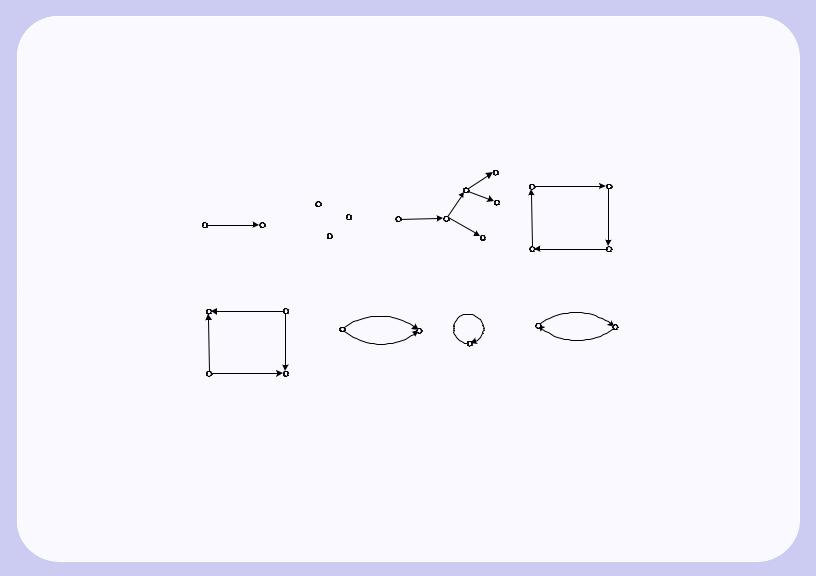
При изображении ориентированных графов (рис. 3.2,а–з) направления ребер отмечаются стрелка- |
|||
|
ми, примыкающими к их концам. Ориентированный граф также может иметь кратные ребра (рис. 3.2,е), |
|||
|
петли (рис. 3.2,ж), а также соединяющие одни и те же вершины ребра, идущие в противоположных на- |
|||
|
правлениях (рис. 3.2,з). |
|||
|
Каждому неориентированному графу можно поставить в соответствие ориентированный граф с тем |
|||
|
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель |
|
же множеством вершин, в котором каждое ребро заменено двумя ориентированными ребрами, инци- |
|||||
|
дентными тем же вершинам и имеющими противоположные направления. Такое соответствие будем |
|||||
|
называть каноническим. |
|||||
Матрица инцидентности и список ребер |
|||||
|
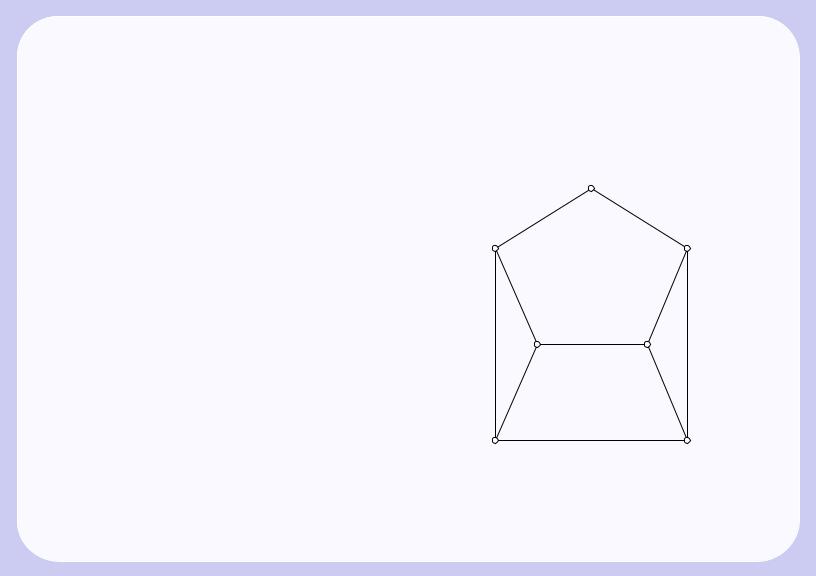
Задать граф — значит описать множества его |
VII |
||||
|
вершин и ребер, а также отношение инцидент- |
|||||
|
ности. Когда граф G — конечный, для описа- |
9 |
||||
|
ния его вершин и ребер достаточно их за- |
V |
10 |
VI |
||
|
нумеровать. Пусть v1v2, . . . , vn — вершины графа |
|||||
|
G; e1e2, . . . , em — его ребра. Отношение инцидент- |
|||||
|
ности можно определить матрицей ||εij||, имею- |
7 |
8 |
|||
|
щей m строк и n столбцов. Столбцы соответству- |
|||||
|
ют вершинам графа, строки — ребрам. Если ребро |
6 |
||||
|
ei инцидентно вершине Vj, то εij = 1, в противном |
4 |
III |
IV |
5 |
|
|
случае εij = 0. Это так называемая матрица ин- |
|||||
|
цидентности неориентированного графа G, ко- |
2 |
3 |
|||
|
торая является одним из способов его определе- |
|||||
|
ния (для графа на рис. 3.3 она дана в табл. 3.1,a). |
1 |
||||
|
I |
II |
||||
|
Рис. 3.3. |
|||||
|
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель |

Таблица 3.1.
|
а) |
б) |
||||||||||||||||||||
|
I |
II |
III |
IV |
V |
VI |
VII |
I |
II |
III |
IV |
V VI |
VII |
|||||||||
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
-1 1 0 |
0 |
0 |
0 |
0 |
||||||||
|
2 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
2 |
-1 0 1 |
0 |
0 |
0 |
0 |
||||||||
|
3 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
3 |
0 -1 0 |
1 |
0 |
0 |
0 |
||||||||
|
4 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
4 |
0 0 -1 0 1 0 |
0 |
|||||||||||
|
5 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
5 |
0 0 -1 0 0 1 |
0 |
|||||||||||
|
6 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
6 |
0 0 -1 |
0 |
0 |
0 |
1 |
||||||||
|
7 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
||||||
|
8 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
||||||||||||||
|
9 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
||||||||||||||
|
10 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
||||||||||||||
|
в) |
г) |
||||||||||||||||||||
|
Рёбра |
Вершины |
Рёбра |
Вершины |
||||||||||||||||||
|
1 |
I, |
II |
1 |
I, |
II |
||||||||||||||||
|
2 |
I, |
III |
2 |
I, |
III |
||||||||||||||||
|
3 |
II, |
IV |
3 |
II, |
IV |
||||||||||||||||
|
4 |
I, |
V |
4 |
III, |
V |
||||||||||||||||
|
5 |
II, |
VI |
5 |
II, |
VI |
||||||||||||||||
|
6 |
III, |
IV |
6 |
III, |
VII |
||||||||||||||||
|
7 |
III, |
V |
7 |
VII, |
VII |
||||||||||||||||
|
8 |
IV, |
VI |
|||||||||||||||||||
|
9 |
V, |
VII |
|||||||||||||||||||
|
10 |
VI, |
VII |
|||||||||||||||||||
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель
|
В матрице инцидентности ||εij|| ориентированного графа G, если вершина Vj — начало ребра ai, то |
|||
|
εij = −1; если vj — конец ai, то εij = 1; если ai — петля, а vj — инцидентная ей вершина, то εij = a, где |
|||
|
α — любое число,отличное от 1, 0 и −1, в остальных случаях εij = 0 (пример — табл. 3.1,б для графа на |
|||
|
рис. 3.4). |
|||
|
В каждой строке матрицы инцидентности для |
II |
3 |
IV |
|
неориентированного или ориентированного гра- |
|||
|
фа только два элемента отличны от 0 (или один, |
1 |
||
|
если ребро является петлей). Поэтому такой спо- |
I |
||
|
соб задания графа εij оказывается недостаточно |
V |
||
|
экономным. Отношение инцидентности можно |
2 |
4 |
|
|
еще задать списком ребер графа. Каждая строка |
|||
|
5 |
VI |
||
|
этого списка соответствует ребру, в ней записаны |
|||
|
номера вершин, инцидентных ему. Для неориен- |
III |
6 |
|
|
тированного графа порядок этих вершин в строке |
VII |
||
|
произволен, для ориентированного первым стоит |
7 |
||
|
номер или другое наименование начала ребра, а |
|||
|
вторым — его конца. В табл. 3.1,в и табл. 3.1,г при- |
|||
|
водятся списки ребер для графов, изображенных |
Рис. 3.4. |
||
|
на рис. 3.3 и 3.4. |
|||
|
По списку ребер графа легко построить его матрицу инцидентности. Действительно, каждая строка |
|||
|
этого списка соответствует строке матрицы с тем же номером. Для неориентированного графа в строке |
|||
|
списка указаны номера элементов строки матрицы инцидентности, равные 1, и для ориентированно- |
|||
|
го графа в этой строке первым стоит номер элемента строки матрицы, равного −1, а вторым — номер |
|||
|
элемента, равного +1. |
|||
|
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель |
Соседние файлы в папке Конспект лекций
- #
- #
- #
- #
