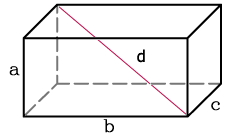
Как найти длины рёбер параллелепипеда по диагонали
Параллелепипед – многогранная геометрическая фигура, обладающая несколькими интересными свойствами. Знание этих свойств помогает в решении задач. Существует, например, определенная связь между его линейными и диагональными измерениями, с помощью которой можно найти длины ребер параллелепипеда по диагонали.

Инструкция
Параллелепипед имеет одну особенность, не свойственную другим фигурам. Его грани попарно параллельны и имеют равные измерения и числовые характеристики, такие как площадь и периметр. Любую пару таких граней можно принять за основания, тогда оставшиеся будут составлять его боковую поверхность.
Можно найти длины рёбер параллелепипеда по диагонали, однако одной этой величины мало. Во-первых, обратите внимание на то, какая разновидность этой пространственной фигуры вам дана. Это может быть правильный параллелепипед, обладающий прямыми углами и равными измерениями, т.е. куб. В этом случае будет достаточно знать длину одной диагонали. Во всех остальных случаях должен быть, как минимум, еще один известный параметр.
Диагонали и длины сторон в параллелепипеде связаны определенным соотношением. Эта формула вытекает из теоремы косинусов и представляет собой равенство суммы квадратов диагоналей и суммы квадратов ребер:
d1² + d2² + d3² + d4² = 4•а² + 4•b² + 4•c², где а – длина, b – ширина и c – высота.
Для куба формула упрощается:
4•d² = 12•а²
а = d/√3.
Пример: найти длину стороны куба, если его диагональ равна 5 см.
Решение.
25 = 3•а²
а = 5/√3.
Рассмотрим прямой параллелепипед, у которого боковые ребра перпендикулярны основаниям, а сами основания являются параллелограммами. Его диагонали попарно равны и связаны с длинами ребер по следующему принципу:
d1² = а² + b² + c² + 2•а•b•cos α;
d2² = а² + b² +c² – 2•а•b•cos α, где α – острый угол между сторонами основания.
Этой формулой можно воспользоваться, если известны, к примеру, одна из сторон и угол или эти величины могут быть найдены по другим условиям задачи. Решение упрощается, когда все углы в основании прямые, тогда:
d1² + d2² = 2•а² + 2•b² + 2•c².
Пример: найдите ширину и высоту прямоугольного параллелепипеда, если ширина b больше длины а на 1 см, высота c – в 2 раза больше, а диагональ d – в 3.
Решение.
Запишите основную формулу квадрата диагонали (в прямоугольном параллелепипеде они равны):
d² = а² + b² + c².
Выразите все измерения через заданную длину а:
b = а + 1;
c = а•2;
d = а•3.
Подставьте в формулу:
9•а² = а² + (а + 1)² + 4•а²
Решите квадратное уравнение:
3•а² – 2•а – 1 = 0
Найдите длины всех ребер:
а = 1; b = 2; c = 2.
Источники:
- формула суммы длин всех рёбер параллелепипеда
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Прямоугольный параллелепипед строится на ребрах трех длин, расположенных под прямым углом друг к другу. Зная ребра параллелепипеда, можно найти все возможные параметры, характеризующие его. В первую очередь, каждая грань параллелепипеда представляет собой прямоугольник с двумя одинаковыми сторонами, периметр же всего объемного тела ищется как умноженная на четыре сумма всех сторон-ребер параллелепипеда.
P=4(a+b+c)
Площадь прямоугольного параллелепипеда складывается из площадей всех его граней, то есть шести прямоугольников, попарно конгруэнтных. Площадь каждого прямоугольника равна произведению его сторон, поэтому чтобы найти площадь параллелепипеда, необходимо сложить эти произведения.
S=2ab+2bc+2ac=2(ab+bc+ac)
Чтобы вычислить объем прямоугольного параллелепипеда, зная его ребро, нужно перемножить их между собой, так как объем любого прямого тела с двумя основаниями равен произведению площади основания на высоту тела, а в основании параллелепипеда находится прямоугольник, площадь которого также равна произведению – его сторон.
V=abc
У прямоугольного параллелепипеда есть четыре диагонали – диагонали его боковых граней и основания, и диагональ самого параллелепипеда, проходящая через его внутреннее пространство. Все диагонали рассчитывается через прямоугольные треугольники по теореме Пифагора, где они являются гипотенузами. Для диагоналей боковых граней и основания катетами являются ребра параллелепипеда, а для четвертой диагонали, катеты представляют собой боковое ребро и диагональ основания. (рис. 22.1,22.2,22.3,22.4)
d_1=√(a^2+c^2 )
d_2=√(a^2+b^2 )
d_3=√(b^2+c^2 )
d_4=√(a^2+〖d_3〗^2 )=√(a^2+b^2+c^2 )
Угол α, образованный внутренней диагональю прямоугольного параллелепипеда и диагональю основания, можно вычислить через отношение тангенса – бокового ребра а и диагонали основания d3.(рис.22.5)
tanα=a/d_3 =a/√(b^2+c^2 )
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм. Правильный параллелепипед это когда все его углы равны 90 градусов.
.
Поделиться расчетом:
Найти боковое ребро правильного параллелепипеда
зная длину ребра и диагональ
Длина ребра параллелепипеда a
Длина ребра параллелепипеда c
Диагональ параллелепипеда d
Вычислить
Установить Боковое ребро параллелепипеда на мобильный
Найти боковое ребро правильного параллелепипеда
зная длину ребра и диагональ
|
||
| Длина ребра параллелепипеда a | ||
| Длина ребра параллелепипеда c | ||
|
Диагональ параллелепипеда d |
||
|
|
||
| Длина ребра параллелепипеда b |
Скачать калькулятор
Рейтинг: 3.3 (Голосов 13)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Сторона треугольника | Стороны прямоугольного треугольника | Стороны равностороннего треугольника | Сторона квадрата |
| Стороны прямоугольника | Стороны ромба | Стороны параллелограмма | Ребро куба |
Главная
Как найти длину ребра объемного параллелепипеда?
-
- 0
-
?
Сара Полоткина
Вопрос задан 22 сентября 2019 в
5 – 9 классы,
Математика.
-
Комментариев (0)
Добавить
Отмена
1 Ответ (-а, -ов)
- По голосам
- По дате
-
- 0
-
Диагонали и длины сторон в параллелепипеде связаны определенным соотношением. Эта формула вытекает из теоремы косинусов и представляет собой равенство суммы квадратов диагоналей и суммы квадратов ребер:
d1² + d2² + d3² + d4² = 4•а² + 4•b² + 4•c², где а – длина, b – ширина и c — высота.
Для куба формула упрощается:
4•d² = 12•а² а = d/√3.
Отмена
Илона Лептикова
Отвечено 22 сентября 2019
-
Комментариев (0)
Добавить
Отмена