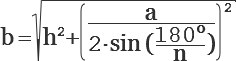Аналитическая геометрия – задача на расчет пирамиды (тетраэдра)
Краткая теория
Вузовская аналитическая геометрия отличается от курса школьной геометрии. Главное отличие состоит в том, что она основным своим инструментом имеет набор алгебраических формул и методов вычислений. В основе аналитической геометрии лежит метод координат.
Аналитическая геометрия имеет набор формул, готовых уравнений и алгоритмов действия. Для успешного и правильного решения главное – разобраться и уделить задаче достаточно времени.
Данная задача является типовой в курсе аналитической геометрии и требует использования различных методов и знаний, таких как декартовые прямоугольные координаты и вектора в пространстве.
Пример решения задачи
Задача
Даны координаты
вершин пирамиды
. Найти:
Сделать чертеж.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Длина ребра
Длину ребра
найдем по
формуле расстояния между 2-мя точками:
Угол между ребрами
Угол между ребрами
и
найдем как угол
между направляющими векторами
и
:
Косинус угла между
векторами:
Угол между ребром и гранью. Векторное произведение
Вычислим угол между
ребром
и гранью
.
Для этого вычислим
координаты нормального вектора плоскости
–им будет
векторное произведение векторов
и
.
Найдем векторное произведение. Для этого
вычислим определитель:
Нормальный вектор
плоскости:
Синус угла:
Площадь грани
Вычислим площадь
грани
. Она будет численно равна половине модуля векторного
произведения векторов
и
:
Искомая площадь:
Объем пирамиды. Смешанное произведение векторов
Вычислим объем
пирамиды. Он будет равен шестой части модуля смешанного произведения векторов
и
:
Для того чтобы вычислить смешанное произведение, необходимо
найти определитель квадратной матрицы, составленной из координат векторов:
Искомый объем
пирамиды:
Уравнение прямой в пространстве
Вычислим уравнение
прямой
. Направляющим
вектором искомой прямой является вектор
. Кроме того, прямая проходит через точку
Уравнение искомой
прямой:
Уравнение плоскости
Вычислим уравнение
плоскости
. Нормальный вектор плоскости
. кроме того, плоскость проходит через точку
-уравнение
грани
Уравнение высоты, опущенной на грань
Составим уравнение
высоты, опущенной на грань
из вершины
:
Нормальный вектор
является
направляющим вектором высоты, кроме того, высота проходит через точку
Искомое уравнение
высоты:
Сделаем схематический чертеж:
/
/
/ Длина ребра пирамиды
Длина ребра пирамиды
Установить Длина ребра пирамиды на мобильный
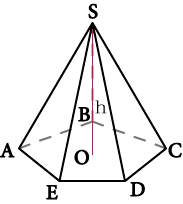
Найти боковое ребро правильной пирамиды
зная длину стороны основания и высоту
|
||
|
Сторона основания пирамиды a |
||
|
Число сторон основания пирамиды n |
||
| Высота пирамиды h | ||
|
|
||
| Длина бокового ребра b |
Скачать калькулятор
Рейтинг: 2.7 (Голосов 6)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Сторона треугольника | Стороны прямоугольного треугольника | Сторона квадрата |
| Стороны прямоугольника | Стороны ромба | Боковое ребро параллелепипеда |
олег
977 дн. назад
а если стороны основания разные?
- reply
Михаил
593 дн. назад
Значит пирамида не правильная.
- reply
Добавить комментарий:
Я не робот
Онлайн решение Пирамиды по координатам вершин
Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольной пирамиды (тетраэдра):
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;
8) основания, площади и уравнения биссекторов;
9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Пример 1:
Даны координаты вершин пирамиды А1А2А3А4.
Найти:
1) координаты и модули векторов А1 А2и А1 А4;
2) угол между ребрами А1 А2и А1 А4;
3) площадь грани А1 А2 А3;
4) объем пирамиды;
5) уравнение прямой А1 А2;
6) уравнение плоскости А1 А2 А3;
7) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3.
Сделать чертеж.
А1 (0; 4; -4), А2 (5; 1; -1), А3 (-1; -1; 3), А4 (0; -3; 7).
Решение от преподавателя:
Пример 2:
Даны координаты вершин пирамиды А1А2А3А4.
Найти: 1) длину ребра А1 А2;
2) угол между ребрами А1 А2и А1 А4;
3) угол между ребром А1 А4 и гранью А1 А2 А3;
4) площадь грани А1 А2 А3;
5) объем пирамиды;
6) уравнение прямой А1 А2;
7) уравнение плоскости А1 А2 А3;
8) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3. Сделать чертеж.
1. А1 (7; 7; 3), А2 (6; 5; 8), А3 (3; 5; 8), А4 (8; 4; 1).
Решение от преподавателя:
Пример 3:
Решение от преподавателя:
Уравнение плоскости.
Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:
|
= 0 |
Уравнение плоскости A1A2A3
(x-3)(1*2-0*3) – (y-2)((-2)*2-3*3) + (z+2)((-2)*0-3*1) = 2x + 13y – 3z-38 = 0
Угол между прямой A1A4 и плоскостью A1A2A3.
Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле:
Уравнение плоскости A1A2A3: 2x + 13y – 3z-38 = 0
Уравнение прямой A1A4:
γ = arcsin(0.267) = 15.486o
Уравнение высоты пирамиды через вершину A4(0,2,2)
Прямая, проходящая через точку M0(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями:
Уравнение плоскости A1A2A3: 2x + 13y – 3z-38 = 0
Уравнение плоскости через вершину A4(0,2,2)
Плоскость, проходящая через точку M0(x0;y0;z0) и параллельная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется уравнением:
A(x-x0) + B(y-y0) + C(z-z0) = 0
Уравнение плоскости A1A2A3: 2x + 13y – 3z-38 = 0
2(x-0)+13(y-2)-3(z-2) = 0
или
2x+13y-3z-20 = 0
Пример 4:
Решение от преподавателя:
Даны координаты пирамиды: A1(0,1,1), A2(3,4,4), A3(-3,9,3), A4(0,5,4)
- Уравнение плоскости.
Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:
|
= 0 |
Уравнение плоскости A1A2A3
(x-0)(3*2-8*3) – (y-1)(3*2-(-3)*3) + (z-1)(3*8-(-3)*3) = -18x – 15y + 33z-18 = 0
Упростим выражение: -6x – 5y + 11z-6 = 0
2) Угол между прямой A1A4 и плоскостью A1A2A3.
Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле:
Уравнение плоскости A1A2A3: -6x – 5y + 11z-6 = 0
Уравнение прямой A1A4:
γ = arcsin(0.193) = 11.128o
3) Уравнение высоты пирамиды через вершину A4(0,5,4)
Прямая, проходящая через точку M0(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями:
Уравнение плоскости A1A2A3: -6x – 5y + 11z-6 = 0
4) Уравнение плоскости через вершину A4(0,5,4)
Плоскость, проходящая через точку M0(x0;y0;z0) и параллельная плоскости
Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется уравнением:
A(x-x0) + B(y-y0) + C(z-z0) = 0
Уравнение плоскости A1A2A3: -6x – 5y + 11z-6 = 0
-6(x-0)-5(y-5)+11(z-4) = 0
или
-6x-5y+11z-19 = 0
5) Координаты вектора A1A4(0;4;3)
Уравнение прямой, проходящей через точку А1(0,1,1) параллельно вектору А1А2(0,4,3) имеет вид:
Пример 5:
Даны координаты вершин пирамиды А1А2А3А4.
Найти: 1) длину ребра А1 А2;
2) угол между ребрами А1 А2и А1 А4;
3) угол между ребром А1 А4 и гранью А1 А2 А3;
4) площадь грани А1 А2 А3;
5) объем пирамиды;
6) уравнение прямой А1 А2;
7) уравнение плоскости А1 А2 А3;
8) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3. Сделать чертеж.
А1 (4; 4; 10), А2 (4; 10; 2), А3 (2; 8; 4), А4 (9; 6; 9).
Решение от преподавателя:
Пример 6:
Решение от преподавателя:
1) Даны координаты вершин пирамиды: A1(0,1,1), A2(3,4,4), A3(-3,9,3), A4(0,5,4)
Координаты векторов.
Координаты векторов: A1A2(3;3;3) A1A4(0;4;3)
Модули векторов (длина ребер пирамиды)
Длина вектора a(X;Y;Z) выражается через его координаты формулой:
Угол между ребрами.
Угол между векторами a1(X1;Y1;Z1), a2(X2;Y2;Z2) можно найти по формуле: 
Найдем угол между ребрами A1A2(3;3;3) и A1A3(0;4;3):
А1 = arccos(0,808)
Найдем площадь грани с учётом геометрического смысла векторного произведения:
S =
Найдем векторное произведение
=i(3*2-8*3) – j(3*2-(-3)*3) + k(3*8-(-3)*3) = -18i – 15j + 33k
3) Объем пирамиды.
Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:
|
|
Координатывекторов:A1A2(3;3;3) A1A3(-3;8;2) A1A4(0;4;3) :
|
|
|
где определитель матрицы равен:
∆ = 3*(8*3-4*2)-(-3)*(3*3-4*3)+0*(3*2-8*3) = 39
Пример 7:
Решение от преподавателя:
- Угол между ребрами.
Угол между векторами a1(X1;Y1;Z1), a2(X2;Y2;Z2) можно найти по формуле:
где a1a2 = X1X2 + Y1Y2 + Z1Z2
Найдем угол между ребрами A1A2(-2;1;3) и A1A3(3;0;2):
γ = arccos(0) = 90.0030 - Площадь грани
Площадь грани можно найти по формуле:
где
Найдем площадь грани A1A2A3
Найдем угол между ребрами A1A2(-2;1;3) и A1A3(3;0;2):
Площадь грани A1A2A3 - Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:
|
|
|
|
|
где определитель матрицы равен:
∆ = (-2)*(0*4-0*2)-3*(1*4-0*3)+(-3)*(1*2-0*3) = -18
Пример 8:
Даны координаты вершин пирамиды А1А2А3А4 . Найти:
1) длину ребра А1А2;
2) угол между рёбрами А1А2 и А1А4 ;
3) угол между ребром А1А4 и гранью А1А2А3;
4) площадь грани А1А2А3;
5) объём пирамиды;
6) уравнение прямой А1А2;
7) уравнение плоскости А1А2А3;
8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3;
Сделать чертёж.
А1(3; 5; 4), А2(8; 7; 4), А3(5; 10; 4), А4(4; 7; 8).
Решение от преподавателя:
1) Длина ребра A1A2;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребрами А1А4 и гранью А1А2А3;
Найдем уравнение стороны А1А4:
Вектор нормали: к плоскости А1А2А3.
4) площадь грани А1А2А3;
5) объем пирамиды;
6) уравнение прямой А1А2;
7) уравнение плоскости А1А2А3;
Итак: z=4 – уравнение плоскости А1А2А3.
8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3.
A4O – высота:
Уравнение A4O:
Т.к. , то
В результате получаем уравнение высоты:
Пример 9:
Даны координаты вершин пирамиды А1А2А3А4.
Найти: 1) длину ребра А1 А2;
2) угол между ребрами А1 А2и А1 А4;
3) угол между ребром А1 А4 и гранью А1 А2 А3;
4) площадь грани А1 А2 А3;
5) объем пирамиды;
6) уравнение прямой А1 А2;
7) уравнение плоскости А1 А2 А3;
8) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3. Сделать чертеж.
А1 (4; 4; 10), А2 (4; 10; 2), А3 (2; 8; 4), А4 (9; 6; 9).
Решение от преподавателя:
Как найти длину ребра пирамиды
Пирамида – это фигура, у которой есть основание в виде многоугольника и боковые грани со сходящимися вверху вершинами. Границы боковых граней называются ребрами. А как же найти длину ребра пирамиды?

Инструкция
Найдите граничные точки ребра, длину которого ищете. Пусть это будут точки А и В.
Задайте координаты точек А и В. Их нужно задавать трехмерными, т.к. пирамида – объемная фигура. Получите А(х1, у1, z1) и B(x2, y2, z2).
Вычислите нужную длину, используя общую формулу: длина ребра пирамиды равняется корню суммы квадратов разниц соответствующих координат граничных точек. Подставьте цифры ваших координат в формулу и найдите длину ребра пирамиды. Таким же образом найдите длину ребер не только правильной пирамиды, но и прямоугольной, и усеченной, и произвольной.
Найдите длину ребра пирамиды, у которой все ребра равны, заданы стороны основания фигуры и известна высота. Определите месторасположение основания высоты, т.е. нижней ее точки. Так как ребра равны, значит можно провести окружность, центром которой будет точка пересечения диагоналей основания.
Проведите прямые линии, соединяющие противоположные углы основания пирамиды. Отметьте точку, где они пересекаются. Эта же точка и будет нижней границей высоты пирамиды.
Найдите длину диагонали прямоугольника с помощью теоремы Пифагора, где сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы. Получите а2+b2=c2, где а и b – катеты, а с – гипотенуза. Гипотенуза тогда будет равна корню из суммы квадратов катетов.
Найдите длину ребра пирамиды. Сначала поделите длину диагонали пополам. Все полученные данные подставьте значения в формулу Пифагора, описанную выше. Аналогично предыдущему примеру найдите корень из суммы квадратов высоты пирамиды и половины диагонали.
Источники:
- как найти длину ребра по координатам
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.