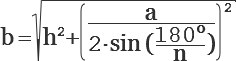Как найти длину ребра пирамиды
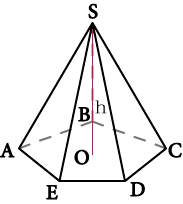
Пирамида – это фигура, у которой есть основание в виде многоугольника и боковые грани со сходящимися вверху вершинами. Границы боковых граней называются ребрами. А как же найти длину ребра пирамиды?

Инструкция
Найдите граничные точки ребра, длину которого ищете. Пусть это будут точки А и В.
Задайте координаты точек А и В. Их нужно задавать трехмерными, т.к. пирамида – объемная фигура. Получите А(х1, у1, z1) и B(x2, y2, z2).
Вычислите нужную длину, используя общую формулу: длина ребра пирамиды равняется корню суммы квадратов разниц соответствующих координат граничных точек. Подставьте цифры ваших координат в формулу и найдите длину ребра пирамиды. Таким же образом найдите длину ребер не только правильной пирамиды, но и прямоугольной, и усеченной, и произвольной.
Найдите длину ребра пирамиды, у которой все ребра равны, заданы стороны основания фигуры и известна высота. Определите месторасположение основания высоты, т.е. нижней ее точки. Так как ребра равны, значит можно провести окружность, центром которой будет точка пересечения диагоналей основания.
Проведите прямые линии, соединяющие противоположные углы основания пирамиды. Отметьте точку, где они пересекаются. Эта же точка и будет нижней границей высоты пирамиды.
Найдите длину диагонали прямоугольника с помощью теоремы Пифагора, где сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы. Получите а2+b2=c2, где а и b – катеты, а с – гипотенуза. Гипотенуза тогда будет равна корню из суммы квадратов катетов.
Найдите длину ребра пирамиды. Сначала поделите длину диагонали пополам. Все полученные данные подставьте значения в формулу Пифагора, описанную выше. Аналогично предыдущему примеру найдите корень из суммы квадратов высоты пирамиды и половины диагонали.
Источники:
- как найти длину ребра по координатам
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
геометрия не моя наука… найти длину ребра пирамиды в основание которой лежит прямоугольник
sasha
Ученик
(214),
на голосовании
7 лет назад
Рассчитать длину ребра пирамиды в основание которого лежит прямоугольник со сторонами 6 и 8 см. высота пирамиды 10 см. помогите если не сложно
Голосование за лучший ответ
Булатова Римма
Искусственный Интеллект
(126417)
7 лет назад
1) Вначале по теореме Пифагора находим длину диагонали основания: d=АС=10 см.
2) Затем рассмотрим диагональное сечение ASC. Половина его – прямоугольный тр-к с катетами h=10 и d/2=5. Опять по теореме Пифагора найдем длину ребра как гипотенузу: V(100+25)=5V5 см.
Длина бокового ребра прямоугольной пирамиды Калькулятор
| Search | ||
| Дом | математика ↺ | |
| математика | Геометрия ↺ | |
| Геометрия | 3D геометрия ↺ | |
| 3D геометрия | Пирамида ↺ | |
| Пирамида | Квадратная пирамида ↺ | |
| Квадратная пирамида | Правая квадратная пирамида ↺ | |
| Правая квадратная пирамида | Длина бокового ребра прямоугольной пирамиды ↺ |
|
✖Высота прямоугольной пирамиды – это длина перпендикуляра от вершины к основанию прямоугольной пирамиды.ⓘ Высота правой квадратной пирамиды [h] |
+10% -10% |
||
|
✖Длина ребра основания прямоугольной пирамиды — это длина прямой линии, соединяющей любые две смежные вершины основания прямоугольной пирамиды.ⓘ Длина ребра основания прямоугольной пирамиды [le(Base)] |
+10% -10% |
|
✖Длина боковой грани прямоугольной пирамиды — это длина прямой линии, соединяющей любую вершину основания с вершиной прямоугольной пирамиды.ⓘ Длина бокового ребра прямоугольной пирамиды [le(Lateral)] |
⎘ копия |
Длина бокового ребра прямоугольной пирамиды Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Высота правой квадратной пирамиды: 15 метр –> 15 метр Конверсия не требуется
Длина ребра основания прямоугольной пирамиды: 10 метр –> 10 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
16.583123951777 метр –> Конверсия не требуется
3 Длина бокового ребра прямоугольной пирамиды Калькуляторы
Длина бокового ребра прямоугольной пирамиды формула
Длина бокового ребра прямоугольной пирамиды = sqrt(Высота правой квадратной пирамиды^2+Длина ребра основания прямоугольной пирамиды^2/2)
le(Lateral) = sqrt(h^2+le(Base)^2/2)
Что такое прямоугольная пирамида?
Прямоугольная пирамида — это квадратная пирамида, вершина которой расположена выше центра основания. Итак, когда воображаемая линия, проведенная из вершины, пересекает основание в его центре под прямым углом. Квадратная пирамида обычно является правильной квадратной пирамидой. Квадратная пирамида — это пирамида с квадратным основанием и четырьмя равнобедренными треугольными гранями, пересекающимися в геометрической точке (вершине). Он имеет 5 граней, в том числе 4 равнобедренных треугольных грани и квадратное основание. Кроме того, у него 5 вершин и 8 ребер.
/
/
/ Длина ребра пирамиды
Длина ребра пирамиды
Установить Длина ребра пирамиды на мобильный
Найти боковое ребро правильной пирамиды
зная длину стороны основания и высоту
|
||
|
Сторона основания пирамиды a |
||
|
Число сторон основания пирамиды n |
||
| Высота пирамиды h | ||
|
|
||
| Длина бокового ребра b |
Скачать калькулятор
Рейтинг: 2.7 (Голосов 6)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Сторона треугольника | Стороны прямоугольного треугольника | Сторона квадрата |
| Стороны прямоугольника | Стороны ромба | Боковое ребро параллелепипеда |
олег
983 дн. назад
а если стороны основания разные?
- reply
Михаил
599 дн. назад
Значит пирамида не правильная.
- reply
Добавить комментарий:
Я не робот
Аналитическая геометрия – задача на расчет пирамиды (тетраэдра)
Краткая теория
Вузовская аналитическая геометрия отличается от курса школьной геометрии. Главное отличие состоит в том, что она основным своим инструментом имеет набор алгебраических формул и методов вычислений. В основе аналитической геометрии лежит метод координат.
Аналитическая геометрия имеет набор формул, готовых уравнений и алгоритмов действия. Для успешного и правильного решения главное – разобраться и уделить задаче достаточно времени.
Данная задача является типовой в курсе аналитической геометрии и требует использования различных методов и знаний, таких как декартовые прямоугольные координаты и вектора в пространстве.
Пример решения задачи
Задача
Даны координаты
вершин пирамиды
. Найти:
Сделать чертеж.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Длина ребра
Длину ребра
найдем по
формуле расстояния между 2-мя точками:
Угол между ребрами
Угол между ребрами
и
найдем как угол
между направляющими векторами
и
:
Косинус угла между
векторами:
Угол между ребром и гранью. Векторное произведение
Вычислим угол между
ребром
и гранью
.
Для этого вычислим
координаты нормального вектора плоскости
–им будет
векторное произведение векторов
и
.
Найдем векторное произведение. Для этого
вычислим определитель:
Нормальный вектор
плоскости:
Синус угла:
Площадь грани
Вычислим площадь
грани
. Она будет численно равна половине модуля векторного
произведения векторов
и
:
Искомая площадь:
Объем пирамиды. Смешанное произведение векторов
Вычислим объем
пирамиды. Он будет равен шестой части модуля смешанного произведения векторов
и
:
Для того чтобы вычислить смешанное произведение, необходимо
найти определитель квадратной матрицы, составленной из координат векторов:
Искомый объем
пирамиды:
Уравнение прямой в пространстве
Вычислим уравнение
прямой
. Направляющим
вектором искомой прямой является вектор
. Кроме того, прямая проходит через точку
Уравнение искомой
прямой:
Уравнение плоскости
Вычислим уравнение
плоскости
. Нормальный вектор плоскости
. кроме того, плоскость проходит через точку
-уравнение
грани
Уравнение высоты, опущенной на грань
Составим уравнение
высоты, опущенной на грань
из вершины
:
Нормальный вектор
является
направляющим вектором высоты, кроме того, высота проходит через точку
Искомое уравнение
высоты:
Сделаем схематический чертеж: