Рычаг представляет собой один из простых механизмов, который служил и продолжает служить людям для облегчения их физического труда. В статье рассмотрим, что такое рычаг, какие виды его бывают и где они применяются, а также поясним, в чем заключается правило рычага.
Рычаг в физике
Несмотря на то что речь идет о простом механизме, он все же имеет свои составные части. Во-первых, это балка или доска, которая предназначена для воздействия на нее двух противоположных сил. Во-вторых, это опора, которая, с геометрической точки зрения, представляет собой ось вращения, вокруг которой может двигаться балка. В зависимости от расположения опоры под балкой различают три типа рычага, которые будут рассмотрены ниже.
Еще одним важным понятием для любого рычага является “плечо”. Под ним понимают часть балки, которая находится между ее концом и опорой при условии, что воздействующие силы приложены к концам балки. Длина плеча играет важную роль при определении условий равновесия рычага.
Рычаг предназначен для преобразования силы в перемещение или, наоборот, перемещения в силу. Другими словами, рассматриваемый простой механизм, используется для перераспределения работы, которую следует выполнить, в пользу приложенной силы или в пользу осуществляемого перемещения. Рисунок ниже показывает пример рычага первого рода.

Когда человечество начало использовать рычаг?
Ответить уверенно на этот вопрос нельзя. Известно, что рычаги с древнейших времен использовались в Месопотамии и Древнем Египте для подъема тар с водой из колодцев и рек.

Единственным письменным свидетельством, которое сохранилось до наших дней, свидетельствующим об использовании рассматриваемого механизма, является всем известный рычаг Архимеда. В работе Плутарха “Параллельные жизни” (100 год до н. э.) говорится, что Архимед в одиночку смог поднять корабль с грузом и пассажирами над поверхностью воды. При этом философ использовал систему блоков и рычагов.
Если подойти к поставленному в названии пункта вопросу более строго, то можно сказать, что человек пользуется рычагом с момента собственного появления в этом мире, ведь наши предплечья и плечи работают по принципу этого простого механизма.
Понятие о моменте силы
Прежде чем переходить к формулировке правила равновесия рычага, рассмотрим понятие крутящего момента или момента силы. В физике под ним понимают величину, равную произведению плеча силы на саму силу. Математически это записывается так:
M = d*F.
Где, F – воздействующая сила, d – плечо силы, которое соответствует расстоянию от точки приложения F до оси вращения. Последний элемент системы, то есть ось вращения, играет принципиальную роль при определении момента M. Без наличия оси вращения нет никакого смысла говорить о действующем моменте силы.
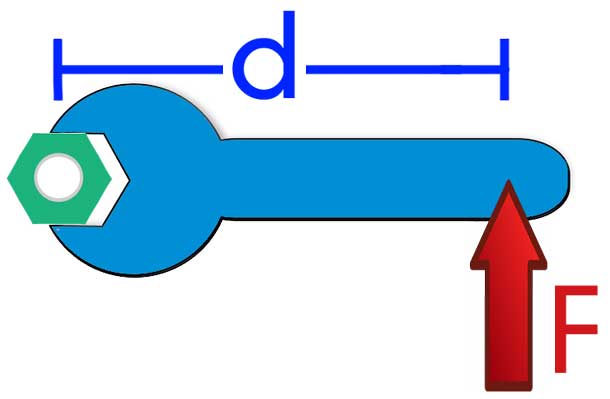
Физический смысл величины M заключается в отражении способности силы F совершить поворот системы вокруг оси. На практике эту способность можно ощутить, если попытаться открутить гайку не гаечным ключом, а руками, или же если постараться открыть дверь не за ручку, а толкая ее вблизи навесных петель.
Во время решения задач момент силы M может приводить как к вращению системы по часовой стрелке, так и против ее хода. В первой случае момент считают отрицательным, во втором – положительным.
Моменты сил и правило рычага
Рассмотрим классический рычаг с двумя плечами, когда опора находится вдали от концов балки. Пример такого механизма изображен ниже.
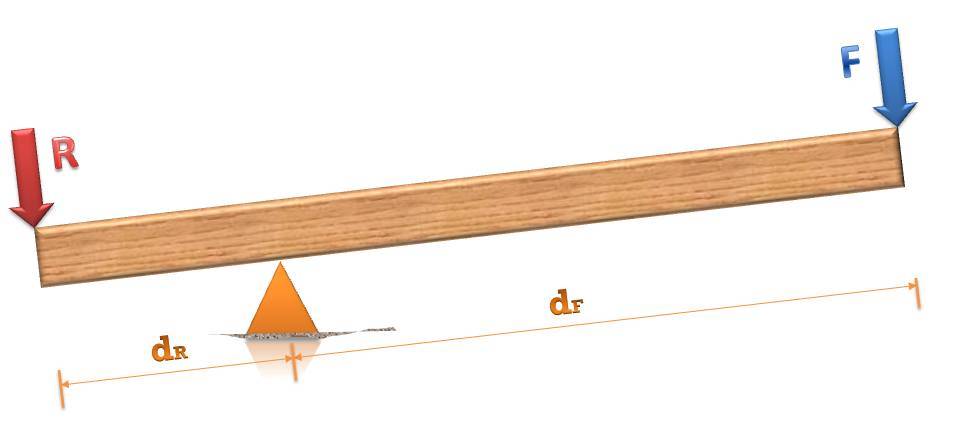
Мы видим, что когда этот рычаг применяют для совершения физической работы, то на него действует две силы:
- внешняя сила F, которую прикладывают для выполнения полезной работы;
- сила R, которая оказывает сопротивление силе F (она выполняет отрицательную работу).
В большинстве случаев сила F создается усилием человека, а сила R представляет собой вес некоторого груза.
Рассматриваемый рычаг будет находиться в равновесии, и перестанет испытывать вращение только тогда, когда сумма действующих на него моментов будет равна нулю. Используя обозначения рисунка выше, и применяя формулу для M, запишем правило равновесия рычага:
R*dR – F*dF = 0.
Заметим, что момент силы F записан со знаком минус, поскольку он стремится повернуть плечо рычага по часовой стрелке. Остается перенести второй член в правую часть равенства, чтобы записать правило рычага:
R*dR = F*dF.
Таким образом, равенство моментов силы действия F и силы противодействия R является достаточным условием равновесия рассматриваемого простого механизма.
Кто установил правило равновесия рычага? Этот вопрос отчасти пересекается с рассмотренным выше историческим. Поскольку сохранились только письменные свидетельства научной деятельности Архимеда, связанной с этим механизмом, то именно он в настоящее время считается тем философом, кто установил правило рычага.
Равновесие рассматриваемой системы обеспечивается не только равенством нулю суммы моментов, но также равенством нулю всех действующих сил. Выше были названы лишь две силы (F и R). На самом же деле существует еще сила реакции опоры, направленная против сил F и R. Реакцию опоры момента силы не создает ввиду нулевой длины ее плеча.
Выигрыш и проигрыш в использовании рычага
Следует четко понимать, что при использовании рычага сохраняется полная энергия системы. Чтобы поднять груз на некоторую высоту, необходимо совершить определенную работу. Поскольку в формуле правила рычага стоит произведение силы на длину плеча, то отмеченную работу можно выполнить как с помощью большей силы, так и с помощью меньшей. Однако в первом случае необходимо будет переместить плечо рычага в вертикальном направлении на малую величину, во втором же случае – на большую величину. Это и есть выигрыш и проигрыш в использовании рычага.
Заметим, что в формуле правила рычага стоят значения моментов. Никакого отношения к работе они не имеют. Момент силы выполняет работу только тогда, когда система за счет его действия поворачивается вокруг оси на некоторый угол.
Виды рычагов
Выше уже упоминалось, что все рычаги относятся к одному из трех типов. В основе классификации лежит относительное расположение сил R, F и опоры. Охарактеризуем все три типа:
- Рычаг 1-го типа, или рода, был показан выше. Опора расположена в нем между силами R и F. В зависимости от длины плеч dR и dF его можно использовать как для выигрыша в пути, так и для выигрыша в силе. Примером этого типа рычага являются ножницы, весы, гвоздодер.
- Рычаг 2-го рода предполагает, что сила R приложена между опорой и силой F. В таком случае получается выигрыш только в силе. Примерами таких рычагов в быту являются орехокол или ручная тачка.
- Рычаг 3-го рода предполагает, что сила F расположена между опорой и грузом R. В этом случае выигрыш возможен только в пути. Использование лопаты, циркуля или удочки для рыбалки – это яркие примеры рычага 3-го рода в работе.

Простой механизм блок
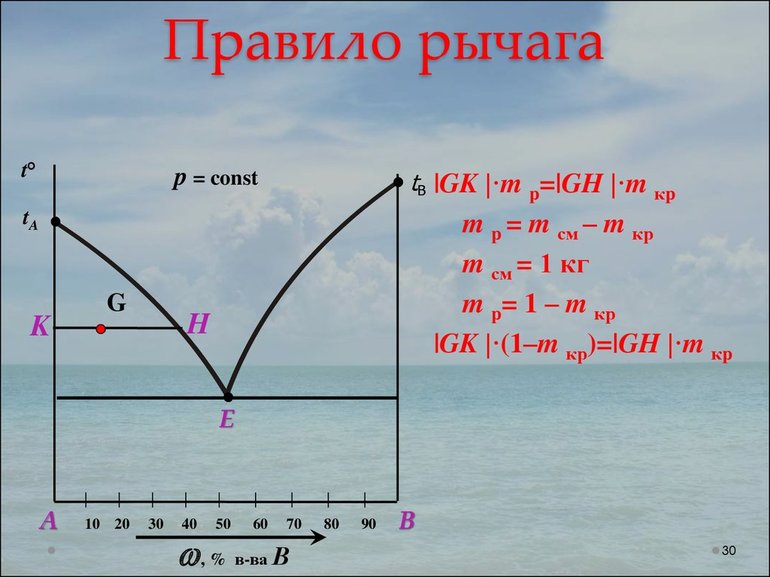
Рассматривая правила рычага, полезно сказать несколько слов о еще одном простом механизме – блоке. Представляет он собой обычный цилиндр с осью вращения, который имеет углубление по периметру своей боковой поверхности. Пример использования неподвижного блока показан ниже.
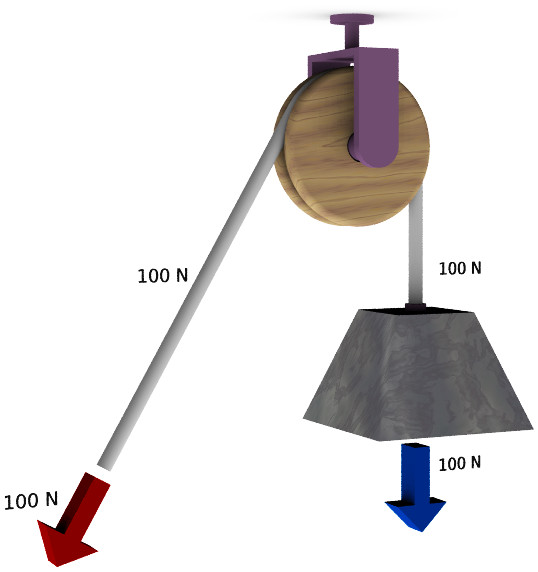
Как видно, выигрыша в силе и пути не происходит, однако неподвижный блок позволяет изменить направление воздействующей силы F.
Применение правила равновесия рычага к блоку производят, когда требуется рассчитать выигрыш в силе при использовании подвижных блоков. Один такой блок позволяет выиграть в 2 раза в силе и во столько же раз проиграть в пути.
Решение задачи
Ручная тачка сделана таким образом, что центр массы груза в ней находится на расстоянии 1/3*l от колеса, где l – длина тачки. Какой массы груз может переместить с помощью тачки человек, если известно, что он может приложить максимальную вертикальную силу F = 200 Н.
Воспользуемся правилом рычага, получим:
F*l = R*1/3*l
F = m*g/3
m = 3*F/g = 3*200/9,81 ≈ 61 кг.
Отметим, что сила F = 200 Н равна весу тела массой всего 20,4 кг. Таким образом, данная ручная тачка позволяет выиграть в 3 раза в силе.
Содержание:
Рычаг:
Взаимодействие может происходить через промежуточные тела.
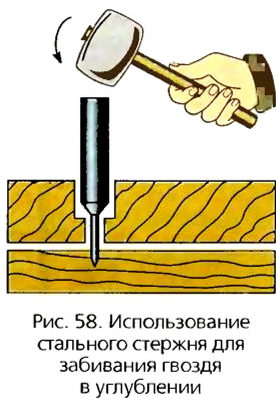
Взаимодействие может происходить не только при непосредственном контакте, но и при наличии промежуточных тел. Таких примеров можно привести большое количество. Так, если мастер забивает гвоздь в углублении, он ставит на головку гвоздя металлический стержень и по нему ударяет молотком (рис. 58). Молоток действует на стержень, который, в свою очередь, уже действует на гвоздь.
Можно ли изменять значения силы
Если взаимодействие между телами происходит через промежуточные тела, то можно изменять силы взаимодействия между ними. Оно может изменить как направление силы, так и ее значение. Одним из примеров такого использования промежуточных тел для взаимодействия между телами является рычаг. В быту и на производстве можно наблюдать много таких примеров.
Часто можно видеть, как тяжелый предмет поднимают или перемещают с помощью металлического стержня (рис. 59). В этом случае стержень называют рычагом.

Что такое рычаг
Рычагом называют жесткий стержень, имеющий ось вращения.
Ось вращения рычага может проходить через один из его концов или посередине рычага – между точками приложения сил.
Под действием нескольких сил рычаг может вращаться или быть неподвижным. В последнем случае говорят, что рычаг уравновешен.
Как уравновесить рычаг
Выясним, при каких условиях рычаг, на который действует несколько сил, будет уравновешен.
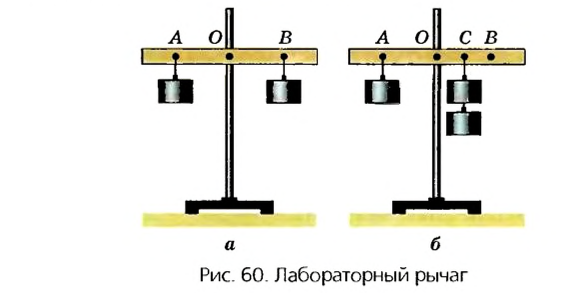
Для этого возьмем деревянную планку с отверстием посередине и поместим ее на оси, закрепленной в штативе (рис. 60). Это и будет рычаг. Слева от оси вращения повесим в точке А на расстоянии 10 см гирьку массой 102 г. В этом случае говорят, что точка А является точкой действия силы 1 Н. Под действием этой силы рычаг начнет вращаться против часовой стрелки. Для того чтобы он не вращался и оставался в горизонтальном положении, на другом конце рычага найдем такую точку В, при закреплении в которой гирьки массой 102 г рычаг перестанет вращаться. Измерив расстояние ОВ, увидим, что оно также равно 10 см. Таким образом, OA = ОВ, если Fl = F2. Если направление действия силы перпендикулярно к направлению оси вращения рычага, то расстояние от его оси вращения к направлению действия силы называют плечом силы.
Если силы, действующие на рычаг, находящийся в равновесии, равны, то равны и плечи этих сил.
Если левую гирьку оставить прикрепленной в точке А, а в точке В подвесить две такие гирьки массой по 102 г каждая, то равновесие рычага нарушится и он начнет вращаться. Достигнуть равновесия в этом случае можно, изменяя положение точки подвеса двух гирек. Так можно установить новое положение точки подвеса С. Измерив оба плеча, увидим, что правое плечо ОС в два раза меньше левого плеча OA.

В случае равновесия рычага плечо большей силы меньше, и наоборот, плечо меньшей силы больше.
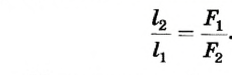
Используя свойства пропорции, получаем

В уравновешенном рычаге плечи сил обратно пропорциональны силам.
Что такое момент силы
Физическую величину, равную произведению силы на плечо, называют моментом силы. Единицей измерения момента силы является ньютон-метр (Н-м).
Сформулируем условие равновесия рычага в общем виде.
Рычаг пребывает в равновесии, если момент силы, вращающий рычаг по часовой стрелке, равен моменту силы, вращающему рычаг против часовой стрелки.
Конструктивно рычаг может быть таким, что силы будут действовать по одну сторону от оси вращения. Условие равновесия для него будет такое же, как и для рычага, рассмотренного выше.
Используя условие равновесия рычага, можно рассчитывать силы, действующие на него, или плечи этих сил.
Пример:
На одно из плеч рычага длиной 30 см действует сила 2 Н. Какая сила должна подействовать на другое плечо этого рычага длиной 15 см, чтобы он оставался неподвижным.
Дано:
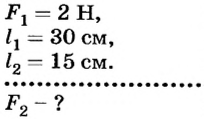
Решение
При условии равновесия рычага 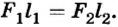 Отсюда
Отсюда
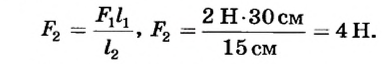
Ответ. На второе плечо рычага должна подействовать сила 4 Н.
Где используют рычаги
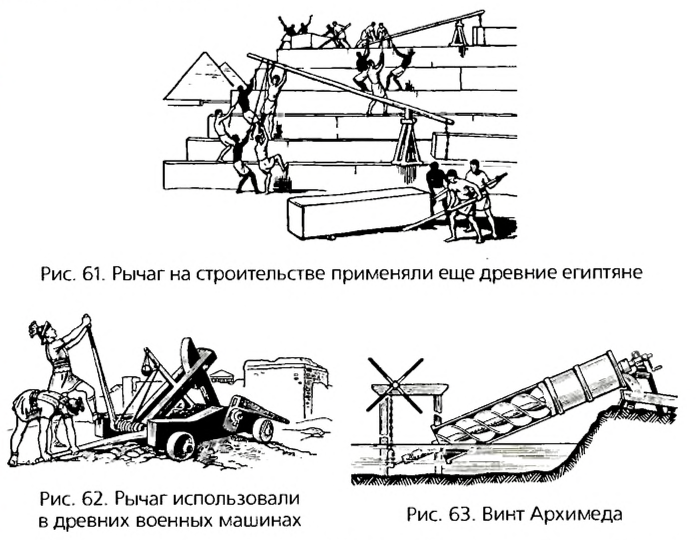
Рычаг известен человеку с того времени, когда человек взял палку, чтобы сбить плод с дерева. И вся следующая история человечества связана с использованием рычагов. Так, исследования историков показывают, что при строительстве пирамид древние египтяне использовали рычаги для поднятия тяжелых блоков на значительную высоту (рис. 61). Историкам науки известно, что древние римляне использовали рычаги для создания различных строительных и военных машин (рис. 62). Значительный вклад в теорию рычагов внес древнегреческий ученый и изобретатель Архимед. Сконструированные им машины помогали оборонять греческие города от захватчиков, подавать воду для орошения полей (рис. 63), перемещать значительные грузы на стройках, выполнять большое количество других подобных работ.
Рычаги широко используются и в современной технике, в самых разнообразных машинах.
Рычагом является стрела подъемного крана, используемого в строительстве. Она дает возможность получить выигрыш в силе или расстоянии. Момент силы, действующей на конце стрелы при подъеме груза, уравновешивается моментом противовеса, находящегося на противоположном конце стрелы.
Принцип рычага используется во многих устройствах и инструментах, которыми мы пользуемся ежедневно. На рисунке 64 изображены некоторые из них. На них легко найти части, исполняющие роль рычагов.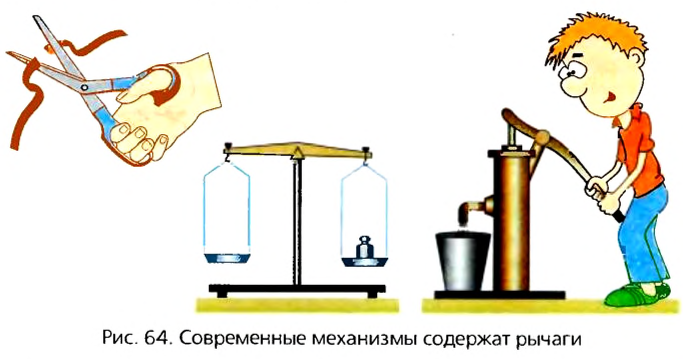
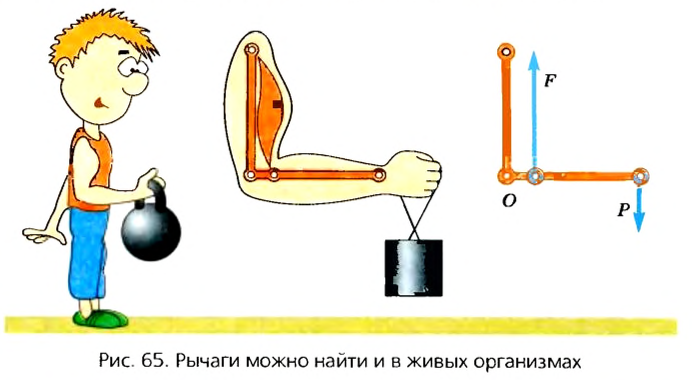
Рычаги можно найти и в живых организмах. По принципу рычага работают руки человека (рис. 65), ноги, голова.
 Архимед (около 287-212 гг. до н. э.) – известный древнегреческий ученый. Научные труды касаются математики, механики, физики и астрономии. Автор многих изобретений и открытий, в том числе машины для орошения полей, винта, рычагов, блоков, военных метательных машин и пр. В его труде «О плавающих телах» изложены основы гидростатики.
Архимед (около 287-212 гг. до н. э.) – известный древнегреческий ученый. Научные труды касаются математики, механики, физики и астрономии. Автор многих изобретений и открытий, в том числе машины для орошения полей, винта, рычагов, блоков, военных метательных машин и пр. В его труде «О плавающих телах» изложены основы гидростатики.
Условие равновесия рычага и момент силы
Как уже отмечалось, рычаг — твёрдое тело, которое может вращаться около неподвижной опоры. Его применяют для изменения направления и значения силы, например для уравновешивания большой силы малой. Рычаг имеет следующие характеристики
(рис. 202).
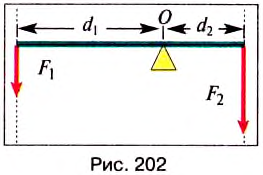
Точка приложения силы — это точка, в которой на рычаг действует другое тело.
Ось вращения — прямая, проходящая через неподвижную точку опоры рычага О, и вокруг которой он может свободно вращаться. Рассмотрим случай, когда ось вращения расположена между точками приложения сил 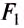 и
и 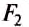 .
.
Линия действия силы — это прямая, вдоль которой направлена сила.
Плечо силы — кратчайшее расстояние от оси вращения тела О до линии действия силы. Плечо силы обозначается буквой d. Единицей плеча силы в СИ является один метр (1 м).
Опыт. Возьмём рычаг, подобный изображённому на рис. 203. На расстоянии 10 см от оси вращения подвесим к нему 6 грузиков, каждый массой по 100 г. Чтобы уравновесить рычаг двумя такими же грузиками, нам придётся их подвесить с другой стороны рычага, но на расстоянии 30 см.
Следовательно, для того чтобы рычаг находился в равновесии, нужно к длинному плечу приложить силу, во столько раз меньшую, во сколько раз его длина больше длины короткого плеча. Такое правило рычага описывают формулой обратно пропорциональной зависимости: 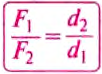 ,
,
где 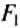 и
и 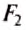 — силы, действующие на рычаг;
— силы, действующие на рычаг; 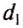 и
и 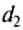 — плечи соответствующих сил. Поэтому правило (условие) равновесия рычага можно сформулировать так.
— плечи соответствующих сил. Поэтому правило (условие) равновесия рычага можно сформулировать так.
Рычаг находится в равновесии тогда, когда значения сил, действующих на него, обратно пропорциональны плечам этих сил.
С тех пор, когда Архимед установил правило рычага, оно просуществовало в первозданном виде почти 1900 лет. И лишь в 1687 г. французский учёный П. Вариньон придал ему более общую форму, используя понятие момента силы.
Момент силы М– это физическая величина, значение которой опре-Г деляется произведением модуля силы F, вращающей тело, и ее плеча d : 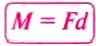 .
.
Единицей момента силы в СИ является один ньютон-метр (1 Н • м), равный моменту силы 1 Н, приложенной к плечу 1 м.
Докажем, что рычаг находится в равновесии под действием двух сил, если значение момента М1 силы, вращающей рычаг против часовой стрелки, равно значению момента М2 силы, вращающей его по часовой стрелке, т.е.: 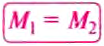
Из правша рычага 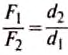 на основе свойства пропорции вытекает
на основе свойства пропорции вытекает
равенство: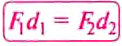 . Но
. Но 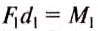 — момент силы, вращающей рычаг против часовой стрелки (рис. 202),
— момент силы, вращающей рычаг против часовой стрелки (рис. 202),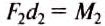 — момент силы, вращающей рычаг по часовой стрелке. Таким образом:
— момент силы, вращающей рычаг по часовой стрелке. Таким образом: 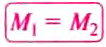 ,
,
что и требовалось доказать. Итак, правило (условие) равновесия рычага можно ещё сформулировать так.
Рычаг находится в равновесии под действием двух сил, если значение момента силы, вращающей рычаг против часовой стрелки, равно значению момента силы, вращающей его по часовой стрелке.
Момент силы — важная физическая величина, она характеризует действие силы, показывает, что оно зависит и от модуля силы, и от её плеча. Например, мы знаем, что действие силы на дверь зависит и от модуля силы, и оттого, где приложена сила: дверь тем легче повернуть, чем дальше от оси вращения приложена сила, действующая на неё; гайку легче открутить длинным гаечным ключом, чем коротким; ведро тем легче вытянуть из колодца, чем длиннее ручка ворота.
Основы статики и равновесие рычага
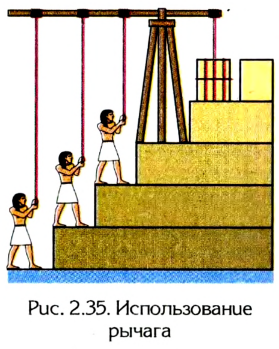
Еще в давние времена люди использовали обычную палку в качестве рычага, выигрывая этим в силе. На рисунке 2.35 показано, как с помощью рычага можно поднять по ступенькам большие каменные глыбы, например для строительства пирамид.
В древних книгах по механике, написанных учеными Греции и Египта, главным образом рассматривались вопросы статики. Важнейшие открытия в этой области принадлежали великому греческому философу Аристотелю, который и дал название «механика» науке, изучающей простейшие движения материальных тел, находящихся в природе или создающихся людьми в процессе их деятельности.
Ученые уже тогда понимали значение статики как одной из основных составляющих фундамента механики. Дальнейшее развитие науки и, особенно, техники подтвердило правильность их вывода: действие огромного количества £ механизмов и машин базируется на законах о равновесии сил.
Аристотель (384-322 до н. э.) – один из известнейших ученых Древней Греции. Изучал вопросы ста-тики, разработал классификацию механических движений, сформулировал закон прямолинейного распространения света, объяснил природу атмосферных явлений и др.
Основы науки о равновесии были заложены еще Архимедом. Именно он ввел в физику такое понятие, как центр тяжести и момент силы относительно точки и оси, определил положение центра тяжести для многих тел и фигур, математически обосновал законы рычага, сформулировал правила приложения параллельных сил.
- Заказать решение задач по физике
В своей работе «О равновесии плоских фигур» Архимед опирался на положения, которые считал само собой разумеющимися:
Архимед (287-212 до н. э.) – древнегреческий физик, математик, исследователь, инженер. Изучал условия равновесия тел, простые механизмы, плавание тел и др. Установил, что соотношение длины любой окружности к ее диаметру (число 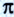 ) колеблется между
) колеблется между 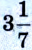 и
и 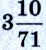 (3,142 – 3,140); на то время это были точные данные.
(3,142 – 3,140); на то время это были точные данные.
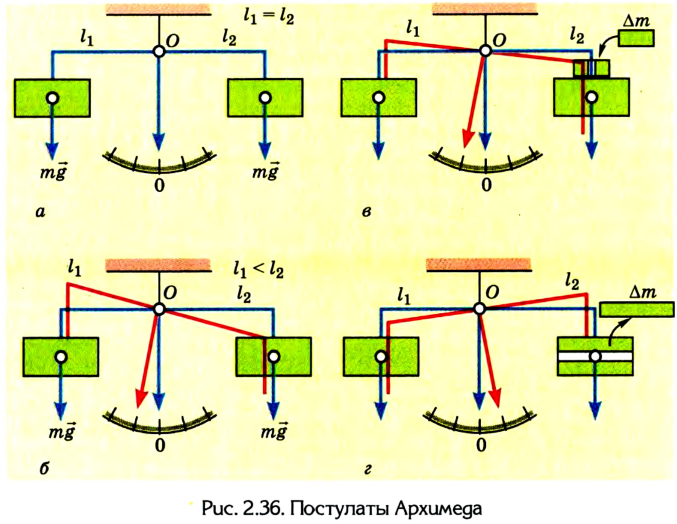
- одинаковые грузы, приложенные к одинаковым плечам рычага, уравновешиваются (рис. 2.36, а);
- одинаковые грузы, приложенные к неодинаковым плечам рычага, не находятся в равновесии; груз, приложенный к более длинному рычагу, падает (рис. 2.36, б);
- если грузы, подвешенные к неодинаковым плечам рычага, уравновешиваются и к одному из них что-либо прибавить, то равновесие нарушится и этот груз будет падать (рис. 2.36, в);
- если при тех же условиях, что в предыдущем случае, один груз уменьшить, то равновесие нарушится, и тогда другой груз будет падать (рис. 2.36, г).
Рычаг находится в равновесии, если плечи сил обратно пропорциональны значениям сил, действующих на него
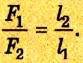
Из этих положений Архимед сделал вывод: грузы пребывают в равновесии, когда плечи рычага обратно пропорциональны грузам:
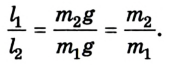
Условия равновесия тел. Устойчивое и неустойчивое равновесие
Равновесие – состояние тела, при котором в рассматриваемой системе отсчета отсутствуют перемещения каких-либо его точек под действием приложенных к нему сил.
Вспомним, что момент силы относительно какой-либо оси равен произведению модуля силы на ее плечо: М = Fl. Плечом силы l называется кратчайшее расстояние от оси вращения до линии действия данной силы. Момент силы считается положительным, если сила стремится повернуть тело по часовой стрелке, и отрицательным, если такое действие противоположно. Для равновесия тел необходимы два условия: 1) геометрическая сумма приложенных к телу сил равна нулю: 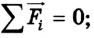
2) алгебраическая сумма моментов сил относительно любой неподвижной оси равна нулю: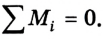
Момент силы: М = Fl.
Условия равновесия тел:
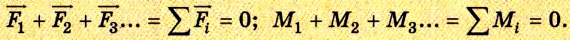
Равновесие устойчивое, если при незначительном смещении тело вновь возвращается в положение равновесия (рис. 2.37).
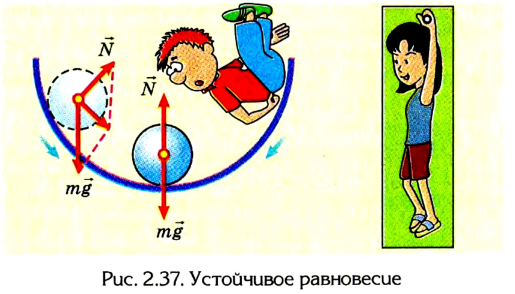
При неустойчивом равновесии незначительное смещение тела вызывает в дальнейшем значительное удаление его от исходного положения (рис. 2.38).
Равновесие тела может быть устойчивым, неустойчивым и безразличным.
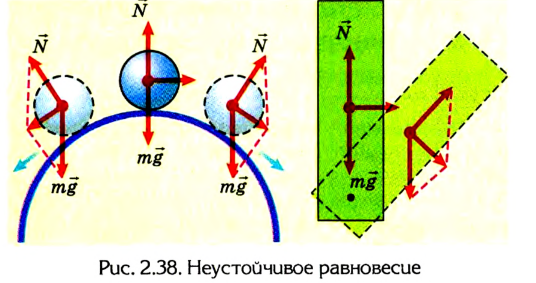
Если любые смещения тела не нарушают его состояния равновесия, то можно говорить о безразличном равновесии (рис. 2.39).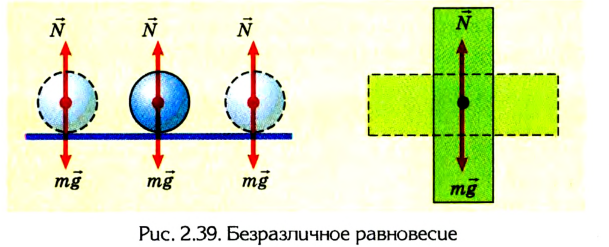
Примеры решения задач на равновесие рычага
Рассмотрим примеры решения задач статики.
Пример №1
Метровая линейка, весом которой можно пренебречь, положена средним делением на подставку и нагружена гирями (рис. 2.40). Какого направления и значения сила должна быть приложена на делении 1 м для того, чтобы линейка находилась в равновесии? Какой будет сила реакции опоры, если приложить эту силу?
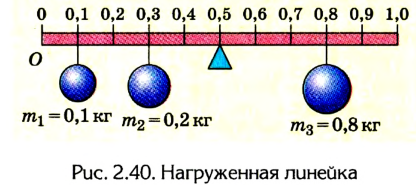
Решение:
Выполняем рисунок в соответствии с условием задачи (рис. 2.41), указав силы и их плечи. Линейка под действием моментов сил может вращаться вокруг неподвижной оси О, которая проходит через точку О. Будем считать положительными все моменты, вращающие систему по часовой стрелке. В задаче это момент силы 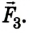 Отрицательные моменты создают силы
Отрицательные моменты создают силы 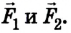
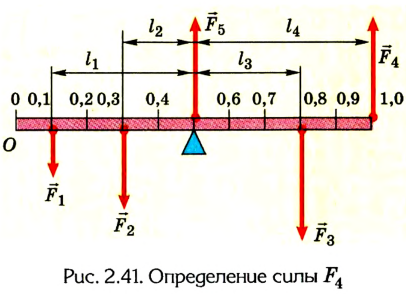
Для упрощения вычислений значение ускорения свободного падения будем считать равным 10 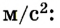
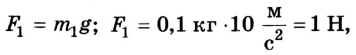
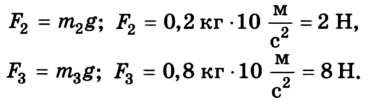
Предположим, что для равновесия системы на конце линейки 1 м должна быть приложена сила 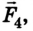 направленная вертикально вверх. Если же мы ошиблись в выборе направления этой силы, то в ответе значение силы получится со знаком “-“. Для решения задачи воспользуемся вторым условием равновесия тела:
направленная вертикально вверх. Если же мы ошиблись в выборе направления этой силы, то в ответе значение силы получится со знаком “-“. Для решения задачи воспользуемся вторым условием равновесия тела:
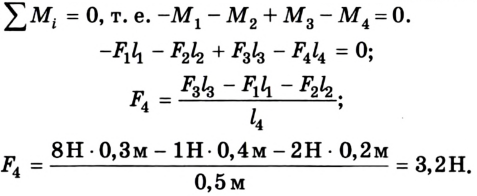
Ответ: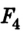 = 3,2H, направление силы выбрано правильно.
= 3,2H, направление силы выбрано правильно.
Пример №2
Метровая линейка, весом которой можно пренебречь, положена крайними точками на две опоры и нагружена гирями, как в предыдущей задаче. Нужно определить силы реакции опор 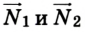 (рис. 2.42).
(рис. 2.42).

Решение:
Чтобы определить силу реакции опоры 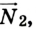 можно воспользоваться таким приемом. Если опору забрать, то для равновесия системы на отметке 1 м необходимо приложить силу, направленную вертикально вверх. Иначе система будет вращаться вокруг оси в точке О линейки по часовой стрелке. Теперь можно применить правило моментов:
можно воспользоваться таким приемом. Если опору забрать, то для равновесия системы на отметке 1 м необходимо приложить силу, направленную вертикально вверх. Иначе система будет вращаться вокруг оси в точке О линейки по часовой стрелке. Теперь можно применить правило моментов:
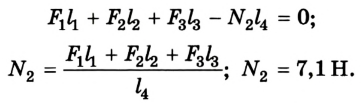
Чтобы определить силу реакции опоры 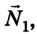 действуем аналогично. Теперь система будет вращаться вокруг оси против часовой стрелки, когда она проходит через отметку 1 м:
действуем аналогично. Теперь система будет вращаться вокруг оси против часовой стрелки, когда она проходит через отметку 1 м: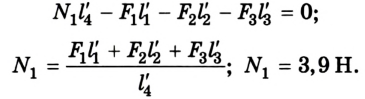
Чтобы найти силы реакции опор, можно воспользоваться правилом сложения параллельных сил. Им же можно пользоваться и для контроля найденных значений.
Ответ: 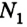 = 3,9 H;
= 3,9 H; 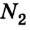 =7,1 Н.
=7,1 Н.
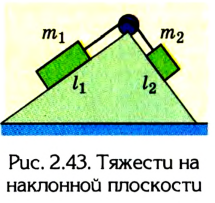
Оригинальный метод решения задач статики был предложен Симоном Сте-вином (1548-1620). Для случаев равновесия тел на наклонной плоскости он доказал, что массы тел соотносятся как длины плоскостей, которые их образуют (рис. 2.43):
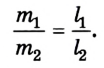
Он же установил принцип сложения статических сил (треугольник сил): три силы, действующие на одну точку, находятся в равновесии тогда, когда они бывают параллельны и пропорциональны трем сторонам плоского треугольника (рис. 2.44). Приведем пример решения одной из задач статики с применением треугольника сил.
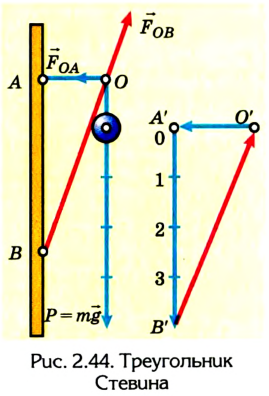
Пример №3
На кронштейне висит лампа весом 4 Н. Найти значение сил упругости в деталях ОА и ОВ.
Дано:
Р = 4 Н
 – ?
– ?
Решение:
Выбираем масштаб построения треугольника. Пусть 1 см на рисунке соответствует значению силы 1 Н. Теперь строим сторону треугольника
А’В’, длина которой известна: 4 см = 4 Н. Эта сторона параллельна направлению силы тяжести, действующей на лампу. Из точки А’ проводим линию, параллельную направлению действия силы в подвесе ОА, а потом из точки В’ – параллельную направлению действия силы в упоре ОВ. На пересечении линий находится точка О’. Таким образом мы получили замкнутый треугольник сил. Зная масштаб, при помощи линейки измеряем значения силы упругости в подвесе ОА (О’А’) и силы реакции в упоре ОВ (О’В’).
- Блоки в физике
- Движение тела под действием нескольких сил
- Наклонная плоскость в физике
- Давление газов и жидкостей
- Равнодействующая сила и движение тела под действием нескольких сил
- Сила давления в физике и единицы давления
- Механическое давление в физике
- Столкновения в физике
Характеристика понятия
Описываемое устройство является довольно простым. Но разбираясь в тонкостях правила рычага в физике, стоит отметить наличие у него нескольких составных частей:
- Балки или доски, на которую воздействует две противоположные силы.
- Опоры, представляющей собой ось вращения. От её размещения под балкой зависит определение типа рычага (таковых существует три).
- Плеча, под которым понимают отрезок доски между её концом и опорой (при этом воздействующие силы должны прилагаться по краям балки). От длины плеча зависят условия равновесия механизма.
Рычаг применяется для преобразования перемещения в силу и наоборот. Таким образом, удаётся добиться перераспределения выполняемой работы в пользу производимого перемещения или прикладываемой силы.
Если рассматривать строение человеческого скелета, можно прийти к выводу, что всем людям с самого рождения предоставляется способность пользоваться системой рычагов. При этом в роли механизма выступают плечи и предплечья.
Начало применения устройства с целью облегчения физической работы датируется древними временами. Имеются сведения, что ещё в Древнем Египте эти приборы шли в ход, когда люди поднимали из реки или колодца наполненный водой сосуд.
В 100 году до нашей эры была издана работа Плутарха под названием «Параллельные жизни». В ней говорится, что Архимеду удалось без посторонней помощи поднять над водой корабль, на борту которого на тот момент находились пассажиры и груз. Для этого были использованы блоки и рычаги. По сей день считается, что именно Архимед изобрёл механизм, поскольку самые древние сохранившиеся письменные работы, свидетельствующие о создании закона, принадлежат перу именно этого философа.
Момент силы
При изучении правила равновесия рычага следует отдельно разобраться в том, что значит единица измерения, называемая моментом силы (или крутящим моментом). Чтобы её изобразить с помощью формулы, необходимо умножить непосредственно величину силы (F) на плечо силы (d).
Схематически это будет изображаться так: М = d x F. Очень важное значение имеет ось вращения. Без её определения действующий момент силы лишён смысла. Использование величины М говорит о способности силы оборачивать систему вокруг оси. Применить её на практике можно на примере гайки, если постараться открутить последнюю без помощи гаечного ключа, а лишь одними руками. Тот же эффект будет наблюдаться и при попытке открыть дверь толчком около петель, а не за ручку.
При решении задач величина М способна приводить к вращению механизм как по ходу часовой стрелки, так и против него. При этом в первом случае момент отрицательный, а во втором — положительный.
Правило рычага
Чтобы разобраться, в чём заключается правило рычага, стоит рассмотреть пример работы классического механизма с двумя плечами и опорой, расположенной далеко от обоих концов доски. Во время применения прибора отмечается действие двух сил на него:
- Внешней F, прикладываемой для осуществления полезной работы.
- R, оказывающей F сопротивление и выполняющей отрицательную работу.

Обычно для создания F прикладываются человеческие усилия, а R определяется массой поднимаемого груза. Механизм достигнет равновесия лишь в том случае, если действующие на него моменты в сумме окажутся равны нулю. С учётом момента силы формулу для правила рычага можно записать так: R х DR — F х DF = 0, где D является плечом силы. F отрицательная из-за того, что стремится оборачивать плечо устройства по кругу в направлении движения часовой стрелки. Если записать формулу в виде равенства, она будет выглядеть так: R х DR = F х DF.
Отсюда следует, что для достижения простым рычагом равновесия достаточно добиться равенства моментов сил действия F и противодействия R. При применении механизма сохраняется энергия системы, свидетельствующая о необходимости проделывания определённой работы во время поднятия груза на какую-либо высоту.
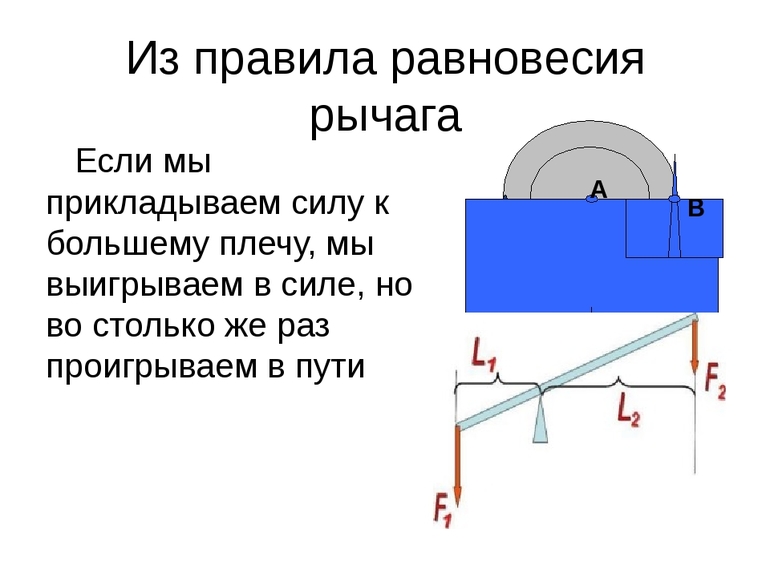
Поскольку для получения значения правила рычага длину плеча умножают на силу, то существует возможность осуществления работы как с применением большей, так и меньшей силы. Но при первом варианте плечо механизма придётся установить на меньшую величину в вертикальном направлении, а второй случай предполагает перемещение плеча на большую величину. Эта особенность называется выигрышем и проигрышем в применении рычага.
Стоит отметить, что значения моментов никак не влияют на работу. Осуществление действия благодаря моменту силы отмечается лишь в тех случаях, когда система начинает поворачиваться на определённый угол по часовой стрелке.
Виды механизмов
Как известно, все рычаги подразделяются на три типа. Основывается эта классификация на относительном расположении опоры к силам R и F. Каждый из видов механизма стоит охарактеризовать отдельно:
- В приборах первого типа опора размещается между R и F. При этом от длины плеч зависит, будет ли рычаг использован для выигрыша в силе либо же в пути. По этому принципу устроена работа ножниц, весов на механике, гвоздодёра.
- Работа устройств второго типа основывается на воздействии силы R, приложенной между F и опорой. Однако использовать такие рычаги можно при расчёте на получение выигрыша лишь в силе. Наиболее простыми примерами устройств считаются ручные тачки и орехоколы.
- Третий тип основывается на размещении F между грузом и опорой. Такие механизмы позволяют получить выигрыш только в пути. Пронаблюдать работу этого типа можно с помощью использования рыболовной удочки, циркуля или лопаты.
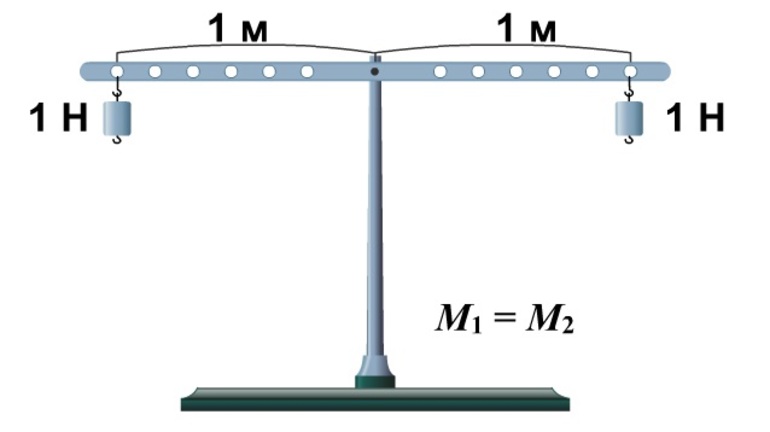
Помимо рычагов, при изучении правила равновесия стоит обратить внимание и на другой простой механизм, называемый блоком. Это цилиндр, оснащённый осью вращения и углублением, сформированным вдоль боковой поверхности. При его применении полностью отсутствует выигрыш в силе и пути, однако, благодаря использованию неподвижного блока, можно поменять направление воздействия F. К устройству применимо правило рычага, но только тогда, когда необходимо добиться выигрыша в силе для подвижных блоков, каждый из которых способен увеличить такое значение вдвое. Но при этом методе идентичная величина проигрывается в пути.
Пример решения задачи
В интернете существует масса приложений со встроенными онлайн-калькуляторами, позволяющими вычислить то или иное значение. Для решения задач по правилу рычага можно воспользоваться этими программами либо же научиться вычислять необходимые величины на основе примеров.
Итак, по условию задачи требуется узнать длину рычага, который позволит 50-килограммовой девушке поднять полуторатонный автомобиль, надавив на механизм всем весом. При этом точка опоры располагается в одном метре от края короткого плеча (D1), где D2 — длинное плечо.
Чтобы выяснить, во сколько раз механизм может дать выигрыш в силе, используется формула F/R=D1/D2. Обе силы оказывают воздействие на рычаг по разные стороны от его опоры, поэтому общая длина доски измеряется по формуле: D = D1+D2.
Согласно условию задачи, величина R, оказывающая действие на плечо D1, это вес автомобиля, обозначаемый Mg. При этом F представляет собой действующую на плечо D2 силу, являющуюся весом девушки (mg). Для получения длины рычага достаточно решить уравнение. Итак, в соответствии с вышеописанной формулой (mg/Mg = D1/D2), чтобы получить D2 необходимо произведение массы авто и длины короткого плеча разделить на вес девушки: (Mg x D1)/mg: D2 = (1500 кг х 1 м)/50 кг = 30 м. Чтобы получить общую длину рычага, понадобится сложить D2 и D1: 30м+1 м. Таким образом, искомая величина будет равна 31 метру.
В наши дни рычаги находят широкое применение как в быту, так и на производстве. Поэтому понимание принципа их работы очень важно практически для каждого человека.
Рычаг, формула
Рычаг — это твердое тело, вращающееся вокруг некоторой оси. Различают Одноплечный рычаг и Двуплечный прямой рычаг и Двуплечный угловой рычаг.
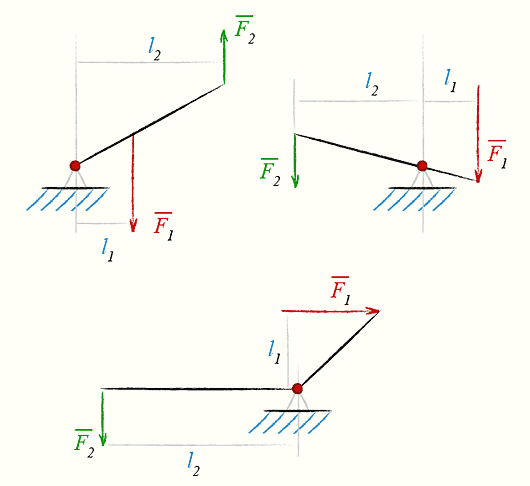
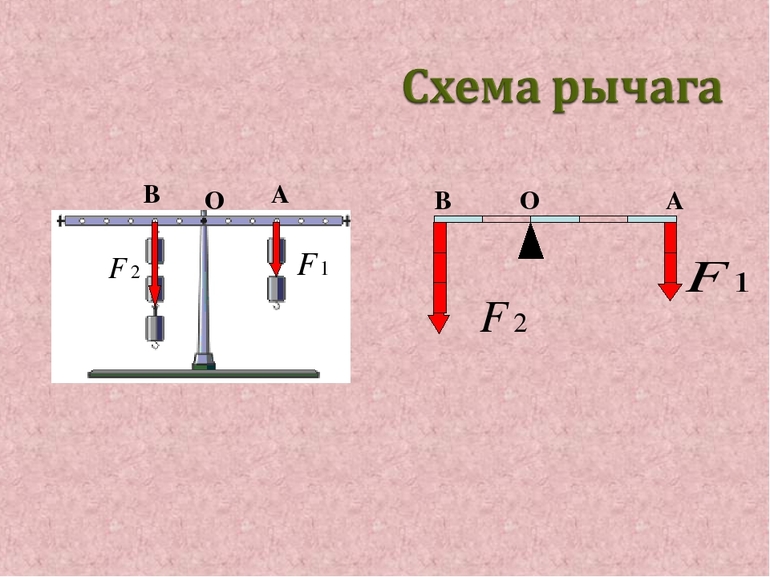
Рычаг, Одноплечный рычаг, Двуплечный прямой рычаг, Двуплечный угловой рычаг
У одноплечного рычага ось расположена на одном из его концов, а силы действующие на него, параллельны но направлены в противоположные стороны (антипараллельны).
У двуплечного прямого рычага ось расположена между точками приложения сил, а силы параллельны и имеют одинаковое направление.
У двуплечного углового рычага ось также расположена между точками приложения сил, а плечи рычага образуют угол, меньший 180°.
Во всех случаях длины плечей находятся, как расстояния от оси вращения до линий действия силы по перпендикуляру.
Правило Рычага
Сила cdot Плечо силы = Нагрузка cdot Плечо нагрузки
Если:
F1 — Нагрузка (Ньютон),
F2 — Сила уравновешивающая нагрузку F1 (Ньютон),
l1 — Плечо нагрузки (метр),
l2 — Плечо силы уравновешивающей нагрузку F1 (метр),
То, используя правило рычага получим:
[ F_1 l_1 = F_2 l_2 ]
Расчет рычага, формулы
- Найти силу воздействия на нагрузку через плечи рычага
- Найти нагрузку для силы воздействия через плечи рычага
- Найти плечо силы для рычага
- Найти плечо нагрузки для рычага
Рычаг |
стр. 390 |
|---|
Рычаг

4.6
Средняя оценка: 4.6
Всего получено оценок: 138.
Обновлено 14 Июля, 2021
4.6
Средняя оценка: 4.6
Всего получено оценок: 138.
Обновлено 14 Июля, 2021
Человек всегда стремился увеличить силу своих мускулов и производить работу, требующую значительных усилий. В результате были сделаны важные изобретения, на основе которых позже придумали сложные механизмы и машины. Главным действующим элементом таких механизмов является рычаг. Рассмотрим принципы, на которых он функционирует.
Рычаг и его структура
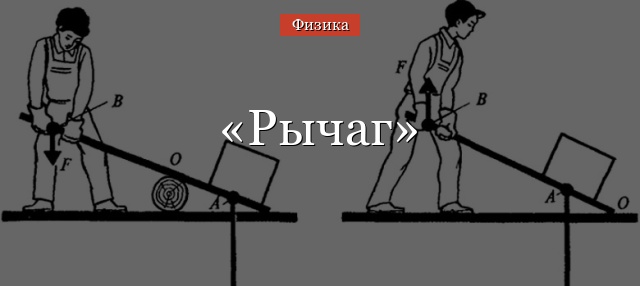
Практически любому человеку приходилось приподнимать тяжелые грузы с помощью длинной палки, короткий конец которой подкладывался под груз. Это очень древнее приспособление, которое называется рычаг.
Рычаг — это твердое тело, которое может вращаться вокруг неподвижной опоры.
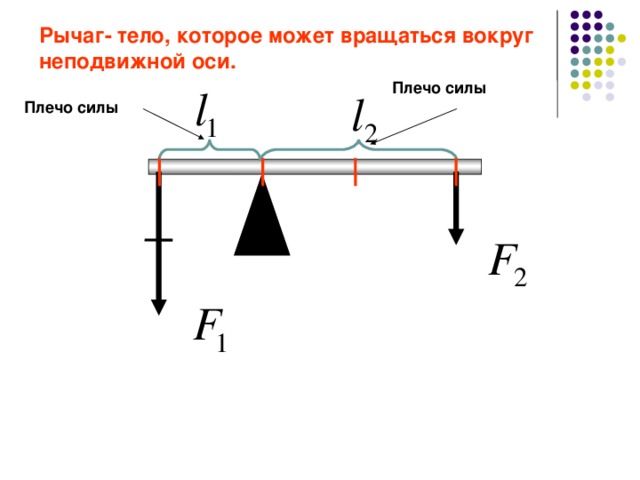
Рычаг может иметь различные виды, но в любом случае он представляет собой твердое тело, имеющее опору, вокруг которой он поворачивается, и на некотором расстоянии от опоры к рычагу прикладываются силы (в простейшем случае — две).
Часть рычага, лежащая между точкой опоры и точкой приложения силы, называется плечом рычага. Силу можно приложить к плечу рычага под разными углами: чтобы учесть это обстоятельство, необходимо определить плечо силы. Из курса физики 7 класса известно, что для нахождения плеча силы необходимо опустить перпендикуляр из точки опоры до линии приложения силы. Длина получившегося перпендикуляра — это и есть плечо силы.
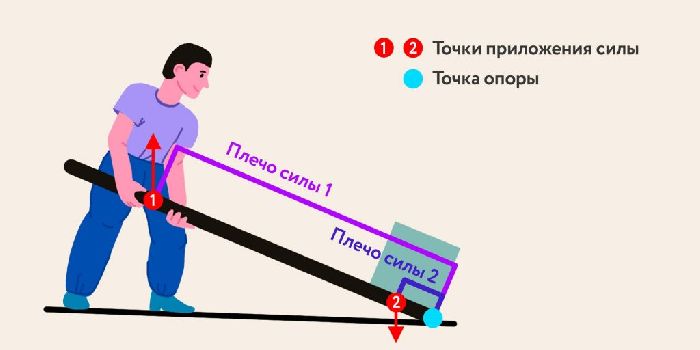
Для приведенного примера, когда палка подкладывается под тяжелый предмет — она является твердым телом, рычагом, а опорой является конец палки, опирающийся в грунт или поверхность пола. К палке приложены две силы — сила тяжести груза и мускульная сила рук. Соответственно, в рычаге два плеча — одно короткое, от точки опоры до точки, упирающейся в груз, и второе — длинное, от точки опоры до точки приложения силы рук. Поскольку силы приложены перпендикулярно палке, плечи обоих сил равны длинам плеч рычага.
Действие рычага
Действие рычага заключается в том, что рычаг поворачивается относительно опоры под действием одной силы и за счет своей твердости создает усилие в другой точке. При этом расстояние от опоры до точек приложения сил может быть различно.
Из опыта известно, что чем длиннее рычаг, тем меньшее усилие требуется для его поворота. Отсюда следует главное свойство рычага, позволяющее решать задачи:
Величина сил, действующих на рычаг, обратно пропорциональна длине плеч этих сил.
То есть, если на рычаг действует сила $F_1$ c плечом $l_1$ и ей противостоит сила $F_2$ c плечом $l_2$, то соотношение сил и плеч рычага можно выразить следующей формулой:
$${F_1 over F_2} = {l_2 over l_1}$$
Это свойство рычага было установлено еще в античности Архимедом.
По преданию, установив это правило, Архимед сказал: «Дайте мне точку опоры, и я сдвину Землю». Однако из приведенной формулы следует, что для того, чтобы Архимед силой своих рук мог бы двигать Землю, длинное плечо рычага должно было бы быть в $10^{23}$ раз длиннее. Всей жизни Архимеду бы не хватило, чтобы с помощью такого длинного плеча сдвинуть Землю даже на толщину волоса.


Что мы узнали?
Рычаг — это простейший механизм, который представляет собой твердое тело, способное поворачиваться вокруг неподвижной опоры. К рычагу на разном расстоянии от опоры приложены силы. Величина сил, действующих на рычаг, обратно пропорциональна длине плеч этих сил.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 138.
А какая ваша оценка?
